2021-2022学年北师大版八年级数学上册第一章 勾股定理 单元测试卷 (Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册第一章 勾股定理 单元测试卷 (Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 321.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 08:28:28 | ||
图片预览

文档简介
第一章 勾股定理 单元测试卷
题号 一 二 三 总分
得分
一、选择题(本大题共10小题,共30分)
将直角三角形的三边长同时扩大2倍,得到的三角形是( )
A. 钝角三角形 B. 直角三角形 C. 锐角三角形 D. 等腰三角形
下列几组数中是勾股数的一组是( )
A. ,, B. ,, C. ,, D. ,,
小明在一个长方形的水池里游泳,长方形的长和宽分别为30m,40m,小明在水池中沿直线最远可以游( )
A. B. C. D.
下列条件能判定ABC为直角三角形的是( )
A. ,, B.
C. ,, D.
如图,小方格都是边长为1的正方形,则ABC中BC边上的高是( )
A. B.
C. D.
如图①是美丽的弦图,蕴含着四个全等的直角三角形.已知每个直角三角形较长的直角边为a,较短的直角边为b,斜边长为c.如图②,现将这四个全等的直角三角形紧密拼接,形成飞镖状,且外围轮廓(实线)的周长为24,OC=3,则该飞镖状图案的面积()
A. B. C. D.
如图所示,有一块长方形场地ABCD,长AB= 20 m、宽AD=10m,中间有一堵墙,高MN=2m,一只蚂蚁要从A点爬到C点,它必须翻过中间那堵墙,则它至少要走( )
A. B. C. D.
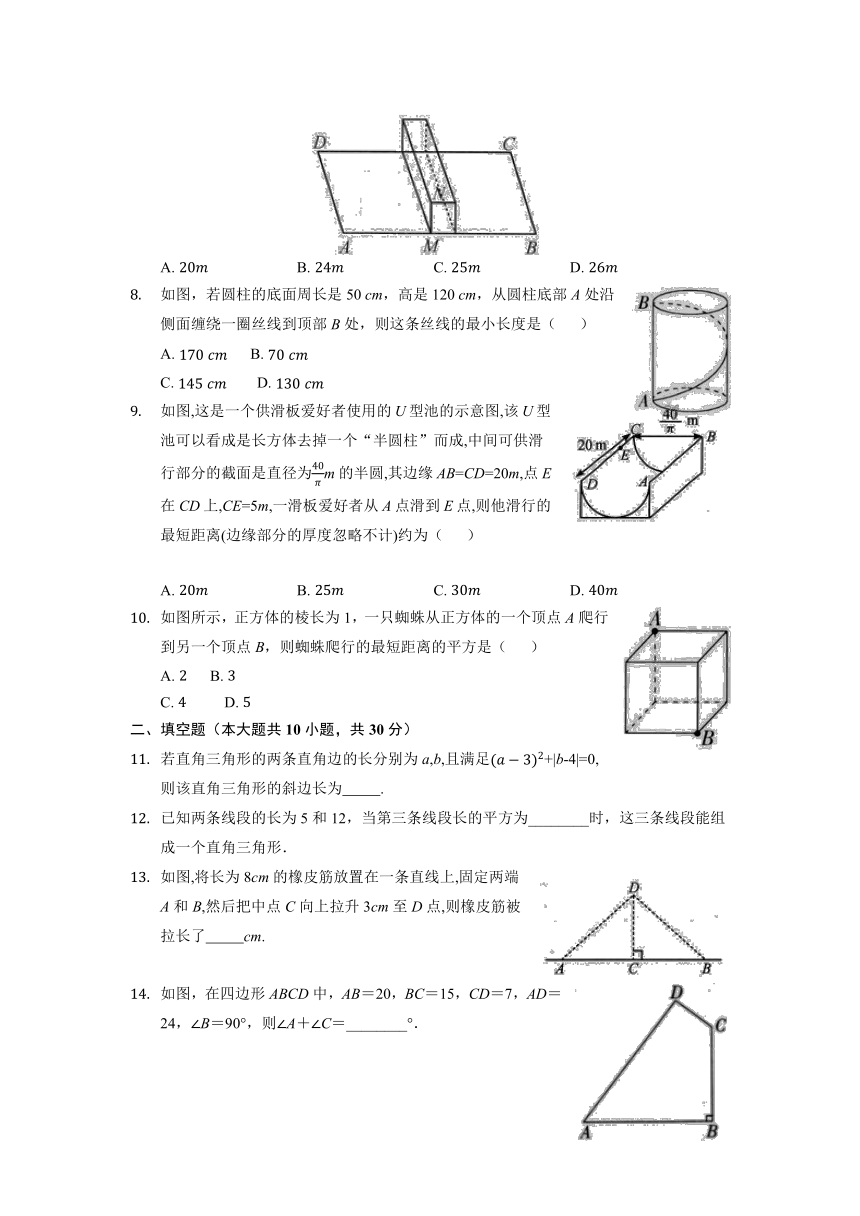
如图,若圆柱的底面周长是50 cm,高是120 cm,从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处,则这条丝线的最小长度是( )
A. B.
C. D.
如图,这是一个供滑板爱好者使用的U型池的示意图,该U型池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为m的半圆,其边缘AB=CD=20m,点E在CD上,CE=5m,一滑板爱好者从A点滑到E点,则他滑行的最短距离(边缘部分的厚度忽略不计)约为( )
A. B. C. D.
如图所示,正方体的棱长为1,一只蜘蛛从正方体的一个顶点A爬行到另一个顶点B,则蜘蛛爬行的最短距离的平方是( )
A. B.
C. D.
二、填空题(本大题共10小题,共30分)
若直角三角形的两条直角边的长分别为a,b,且满足+|b-4|=0,则该直角三角形的斜边长为 .
已知两条线段的长为5和12,当第三条线段长的平方为________时,这三条线段能组成一个直角三角形.
如图,将长为8cm的橡皮筋放置在一条直线上,固定两端A和B,然后把中点C向上拉升3cm至D点,则橡皮筋被拉长了 cm.
如图,在四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°,则∠A+∠C=________°.
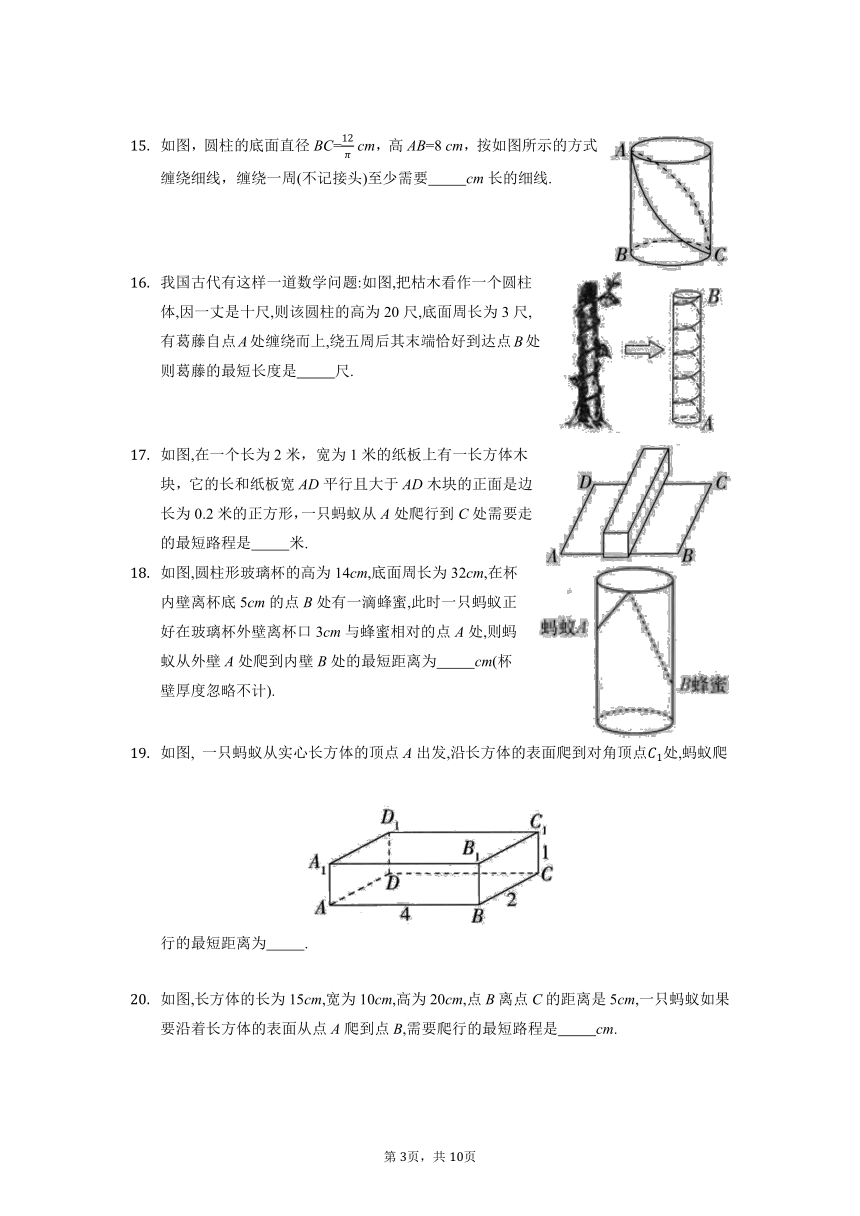
如图,圆柱的底面直径BC= cm,高AB=8 cm,按如图所示的方式缠绕细线,缠绕一周(不记接头)至少需要 cm长的细线.
我国古代有这样一道数学问题:如图,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则葛藤的最短长度是 尺.
如图,在一个长为2米,宽为1米的纸板上有一长方体木块,它的长和纸板宽AD平行且大于AD木块的正面是边长为0.2米的正方形,一只蚂蚁从A处爬行到C处需要走的最短路程是 米.
如图,圆柱形玻璃杯的高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在玻璃杯外壁离杯口3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处爬到内壁B处的最短距离为 cm(杯壁厚度忽略不计).
如图, 一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点处,蚂蚁爬行的最短距离为 .
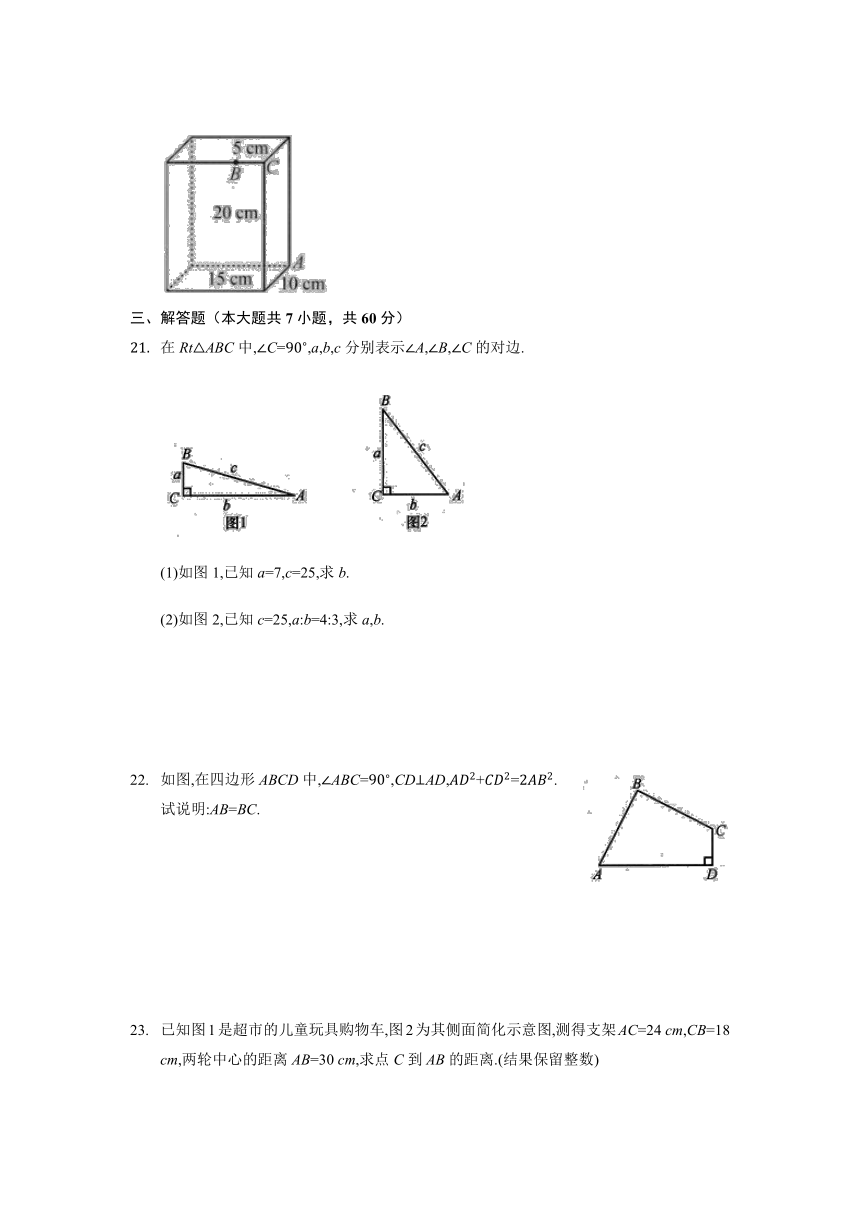
如图,长方体的长为15cm,宽为10cm,高为20cm,点B离点C的距离是5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短路程是 cm.
三、解答题(本大题共7小题,共60分)
在RtABC中,C=,a,b,c分别表示A,B,C的对边.
(1)如图1,已知a=7,c=25,求b.
(2)如图2,已知c=25,a:b=4:3,求a,b.
如图,在四边形ABCD中,ABC=,CDAD,+=.试说明:AB=BC.
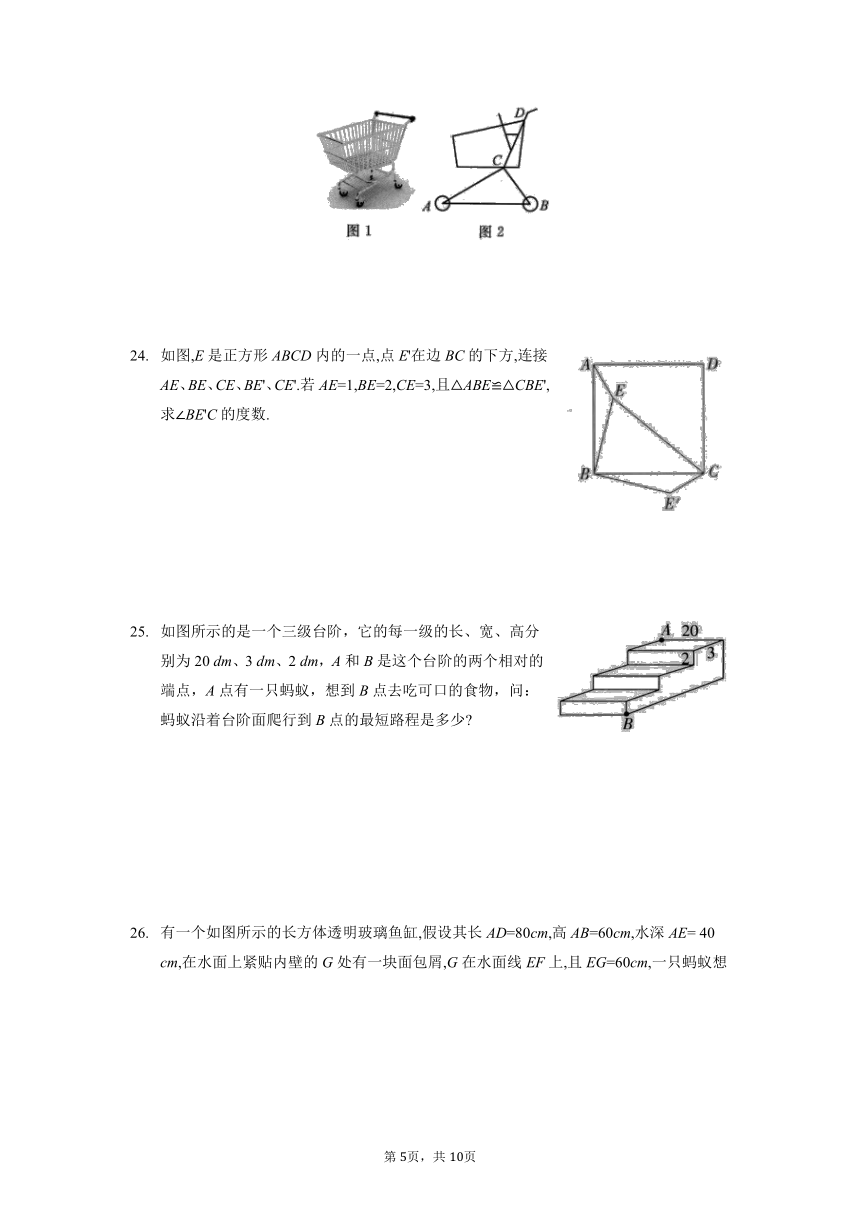
已知图1是超市的儿童玩具购物车,图2为其侧面简化示意图,测得支架AC=24 cm,CB=18 cm,两轮中心的距离AB=30 cm,求点C到AB的距离.(结果保留整数)
如图,E是正方形ABCD内的一点,点E'在边BC的下方,连接AE、BE、CE、BE'、CE'.若AE=1,BE=2,CE=3,且ABECBE',求BE'C的度数.
如图所示的是一个三级台阶,它的每一级的长、宽、高分别为20 dm、3 dm、2 dm,A和B是这个台阶的两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,问:蚂蚁沿着台阶面爬行到B点的最短路程是多少
有一个如图所示的长方体透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深AE= 40 cm,在水面上紧贴内壁的G处有一块面包屑,G在水面线EF上,且EG=60cm,一只蚂蚁想从鱼缸外的A点沿鱼缸壁爬进鱼缸内的G处吃面包屑.
(1) 该蚂蚁应该沿怎样的路线爬行才能使路程最短呢 请你画出它爬行的路线,并用箭头标注.
(2)蚂蚁爬行的最短路线为 cm.
如图,圆柱形杯子高为7 cm,底面周长为18 cm,在杯口点B处有一滴蜂蜜,此时蚂蚁在杯外底部与蜂蜜相对的点A处.
(1)求蚂蚁从A处爬行到B处的最短距离的平方;
(2)若蚂蚁出发时发现蜂蜜正以1 cm/s的速度沿杯内壁下滑,蚂蚁出发后5秒吃到了蜂蜜,求蚂蚁的平均速度至少是多少.
参考答案
1.【答案】B
2.【答案】C
3.【答案】C
4.【答案】D
5.【答案】A
6.【答案】D
7.【答案】D
8.【答案】D
9.【答案】B
10.【答案】D
11.【答案】5
12.【答案】169或119
13.【答案】2
14.【答案】180
15.【答案】20
16.【答案】25
17.【答案】2.6
18.【答案】20
19.【答案】5
20.【答案】25
21.【答案】解:(1)b=24;
(2)a=20,b=15.
22.【答案】解:连接AC,
因为CDAD,
所以D=.
所以+==.
又因为B=,
所以+=.
所以+ =,即=.
所以AB=BC.
23.【答案】解:过点C作CEAB于点E,则CE的长即点C到AB的距离.
在ABC中,
AC=24,CB=18,AB=30,
+=+=900,==900,即+=.
ABC为直角三角形,且ACB=.
=ACBC=CEAB,
ACBC=CEAB,即2418=CE30.
CE=14.414.
答:点C到AB的距离约为14 cm.
24.【答案】解:如图,连接EE'.
ABECBE',
BE=BE'=2, AE=CE'=1,ABE=CBE'.
四边形ABCD是正方形,
ABC=,即ABE+EBC=.
CBE'+ EBC=,即EBE'=.
BEE'为等腰直角三角形.
=+=8,BE'E=.
==9, ==1,
+=.
EE'C=.
BE'C=BE'E+EE'C=
25.【答案】解:经分析,如图,
把台阶看成是由纸片折成的,将其拉平成一张长方形(宽为33+23 =15 dm,长为20 dm)
的纸,
连接AB,则线段AB即为最短路径,
因为=+=625,
所以AB=25 dm,
即蚂蚁沿着台阶面爬行到B点的最短路程是25 dm.
26.【答案】解:(1)作点A关于BC的对称点A',连接A'G交BC于点Q,
连接AQ,蚂蚁沿着AQG的路线爬行时,路程最短.
(2)100
27.【答案】解:(1)蚂蚁从A处爬行到B处的最短距离的平方为 130.
(2)蚂蚁的平均速度至少是3 cm/s.
第7页,共10页
题号 一 二 三 总分
得分
一、选择题(本大题共10小题,共30分)
将直角三角形的三边长同时扩大2倍,得到的三角形是( )
A. 钝角三角形 B. 直角三角形 C. 锐角三角形 D. 等腰三角形
下列几组数中是勾股数的一组是( )
A. ,, B. ,, C. ,, D. ,,
小明在一个长方形的水池里游泳,长方形的长和宽分别为30m,40m,小明在水池中沿直线最远可以游( )
A. B. C. D.
下列条件能判定ABC为直角三角形的是( )
A. ,, B.
C. ,, D.
如图,小方格都是边长为1的正方形,则ABC中BC边上的高是( )
A. B.
C. D.
如图①是美丽的弦图,蕴含着四个全等的直角三角形.已知每个直角三角形较长的直角边为a,较短的直角边为b,斜边长为c.如图②,现将这四个全等的直角三角形紧密拼接,形成飞镖状,且外围轮廓(实线)的周长为24,OC=3,则该飞镖状图案的面积()
A. B. C. D.
如图所示,有一块长方形场地ABCD,长AB= 20 m、宽AD=10m,中间有一堵墙,高MN=2m,一只蚂蚁要从A点爬到C点,它必须翻过中间那堵墙,则它至少要走( )
A. B. C. D.
如图,若圆柱的底面周长是50 cm,高是120 cm,从圆柱底部A处沿侧面缠绕一圈丝线到顶部B处,则这条丝线的最小长度是( )
A. B.
C. D.
如图,这是一个供滑板爱好者使用的U型池的示意图,该U型池可以看成是长方体去掉一个“半圆柱”而成,中间可供滑行部分的截面是直径为m的半圆,其边缘AB=CD=20m,点E在CD上,CE=5m,一滑板爱好者从A点滑到E点,则他滑行的最短距离(边缘部分的厚度忽略不计)约为( )
A. B. C. D.
如图所示,正方体的棱长为1,一只蜘蛛从正方体的一个顶点A爬行到另一个顶点B,则蜘蛛爬行的最短距离的平方是( )
A. B.
C. D.
二、填空题(本大题共10小题,共30分)
若直角三角形的两条直角边的长分别为a,b,且满足+|b-4|=0,则该直角三角形的斜边长为 .
已知两条线段的长为5和12,当第三条线段长的平方为________时,这三条线段能组成一个直角三角形.
如图,将长为8cm的橡皮筋放置在一条直线上,固定两端A和B,然后把中点C向上拉升3cm至D点,则橡皮筋被拉长了 cm.
如图,在四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°,则∠A+∠C=________°.
如图,圆柱的底面直径BC= cm,高AB=8 cm,按如图所示的方式缠绕细线,缠绕一周(不记接头)至少需要 cm长的细线.
我国古代有这样一道数学问题:如图,把枯木看作一个圆柱体,因一丈是十尺,则该圆柱的高为20尺,底面周长为3尺,有葛藤自点A处缠绕而上,绕五周后其末端恰好到达点B处,则葛藤的最短长度是 尺.
如图,在一个长为2米,宽为1米的纸板上有一长方体木块,它的长和纸板宽AD平行且大于AD木块的正面是边长为0.2米的正方形,一只蚂蚁从A处爬行到C处需要走的最短路程是 米.
如图,圆柱形玻璃杯的高为14cm,底面周长为32cm,在杯内壁离杯底5cm的点B处有一滴蜂蜜,此时一只蚂蚁正好在玻璃杯外壁离杯口3cm与蜂蜜相对的点A处,则蚂蚁从外壁A处爬到内壁B处的最短距离为 cm(杯壁厚度忽略不计).
如图, 一只蚂蚁从实心长方体的顶点A出发,沿长方体的表面爬到对角顶点处,蚂蚁爬行的最短距离为 .
如图,长方体的长为15cm,宽为10cm,高为20cm,点B离点C的距离是5cm,一只蚂蚁如果要沿着长方体的表面从点A爬到点B,需要爬行的最短路程是 cm.
三、解答题(本大题共7小题,共60分)
在RtABC中,C=,a,b,c分别表示A,B,C的对边.
(1)如图1,已知a=7,c=25,求b.
(2)如图2,已知c=25,a:b=4:3,求a,b.
如图,在四边形ABCD中,ABC=,CDAD,+=.试说明:AB=BC.
已知图1是超市的儿童玩具购物车,图2为其侧面简化示意图,测得支架AC=24 cm,CB=18 cm,两轮中心的距离AB=30 cm,求点C到AB的距离.(结果保留整数)
如图,E是正方形ABCD内的一点,点E'在边BC的下方,连接AE、BE、CE、BE'、CE'.若AE=1,BE=2,CE=3,且ABECBE',求BE'C的度数.
如图所示的是一个三级台阶,它的每一级的长、宽、高分别为20 dm、3 dm、2 dm,A和B是这个台阶的两个相对的端点,A点有一只蚂蚁,想到B点去吃可口的食物,问:蚂蚁沿着台阶面爬行到B点的最短路程是多少
有一个如图所示的长方体透明玻璃鱼缸,假设其长AD=80cm,高AB=60cm,水深AE= 40 cm,在水面上紧贴内壁的G处有一块面包屑,G在水面线EF上,且EG=60cm,一只蚂蚁想从鱼缸外的A点沿鱼缸壁爬进鱼缸内的G处吃面包屑.
(1) 该蚂蚁应该沿怎样的路线爬行才能使路程最短呢 请你画出它爬行的路线,并用箭头标注.
(2)蚂蚁爬行的最短路线为 cm.
如图,圆柱形杯子高为7 cm,底面周长为18 cm,在杯口点B处有一滴蜂蜜,此时蚂蚁在杯外底部与蜂蜜相对的点A处.
(1)求蚂蚁从A处爬行到B处的最短距离的平方;
(2)若蚂蚁出发时发现蜂蜜正以1 cm/s的速度沿杯内壁下滑,蚂蚁出发后5秒吃到了蜂蜜,求蚂蚁的平均速度至少是多少.
参考答案
1.【答案】B
2.【答案】C
3.【答案】C
4.【答案】D
5.【答案】A
6.【答案】D
7.【答案】D
8.【答案】D
9.【答案】B
10.【答案】D
11.【答案】5
12.【答案】169或119
13.【答案】2
14.【答案】180
15.【答案】20
16.【答案】25
17.【答案】2.6
18.【答案】20
19.【答案】5
20.【答案】25
21.【答案】解:(1)b=24;
(2)a=20,b=15.
22.【答案】解:连接AC,
因为CDAD,
所以D=.
所以+==.
又因为B=,
所以+=.
所以+ =,即=.
所以AB=BC.
23.【答案】解:过点C作CEAB于点E,则CE的长即点C到AB的距离.
在ABC中,
AC=24,CB=18,AB=30,
+=+=900,==900,即+=.
ABC为直角三角形,且ACB=.
=ACBC=CEAB,
ACBC=CEAB,即2418=CE30.
CE=14.414.
答:点C到AB的距离约为14 cm.
24.【答案】解:如图,连接EE'.
ABECBE',
BE=BE'=2, AE=CE'=1,ABE=CBE'.
四边形ABCD是正方形,
ABC=,即ABE+EBC=.
CBE'+ EBC=,即EBE'=.
BEE'为等腰直角三角形.
=+=8,BE'E=.
==9, ==1,
+=.
EE'C=.
BE'C=BE'E+EE'C=
25.【答案】解:经分析,如图,
把台阶看成是由纸片折成的,将其拉平成一张长方形(宽为33+23 =15 dm,长为20 dm)
的纸,
连接AB,则线段AB即为最短路径,
因为=+=625,
所以AB=25 dm,
即蚂蚁沿着台阶面爬行到B点的最短路程是25 dm.
26.【答案】解:(1)作点A关于BC的对称点A',连接A'G交BC于点Q,
连接AQ,蚂蚁沿着AQG的路线爬行时,路程最短.
(2)100
27.【答案】解:(1)蚂蚁从A处爬行到B处的最短距离的平方为 130.
(2)蚂蚁的平均速度至少是3 cm/s.
第7页,共10页
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
