新人教版七年级上1.5.1乘方(第一课时)
文档属性
| 名称 | 新人教版七年级上1.5.1乘方(第一课时) |  | |
| 格式 | zip | ||
| 文件大小 | 517.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-25 07:01:28 | ||
图片预览











文档简介
(共32张PPT)
盘锦四完中:马英欣
(1)边长为2cm的正方形的面积如何表示?
(2)棱长为2cm的正方体的体积如何表示?
读作:2的平方(2的二次方)
读作:2的立方(2的三次方)
2×2记作
2
2×2×2记作2
3
(1)2×2=4(cm2)
(2)2×2×2=8(cm3)
思考
这两个算式的共同点是什么?
2×2和2×2×2都是相同因数的乘法
为了简便
活动1
(1)边长为a的正方形的面积如何表示?
(2)棱长为a的正方体的体积如何表示?
记作
记作
读作:a的平方(a的二次方)
读作:a的立方(a的三次方)
4个a相乘呢?
5个a相乘呢?
100个a相乘呢?
活动2
猜一猜
(-2)× (-2)× (-2)×(-2)
记作:
读作:
(-
)
(-
)
(-
)
(-
)
(-
)
记作:
读作:
一般地,n个相同的因数a 相乘,即
记作: 。
(-2)4
-2的四次方
(- )
2
5
5
(- )
2
5
的五次方
读作:a的n次方
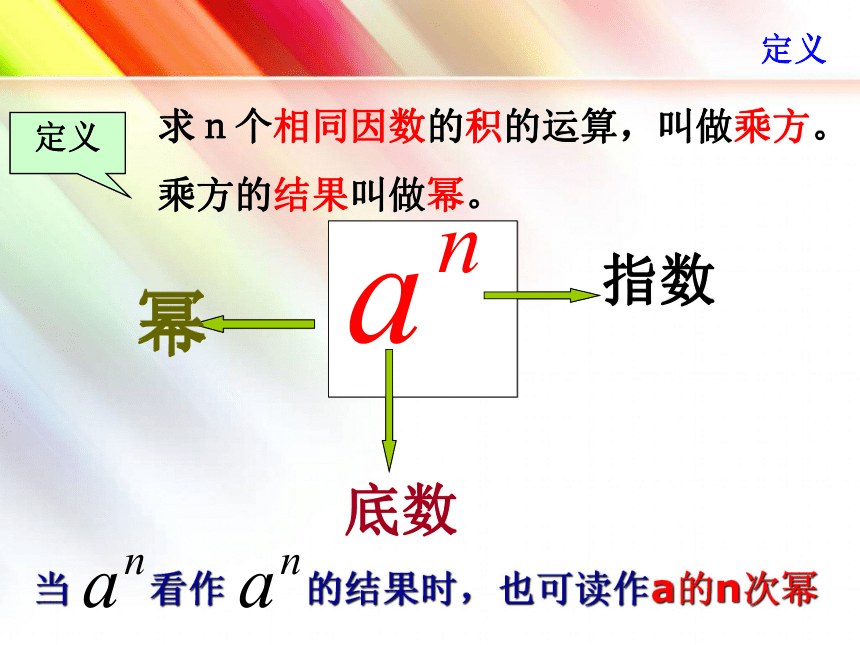
求n个相同因数的积的运算,叫做乘方。
乘方的结果叫做幂。
定义
指数
底数
幂
当 看作 的结果时,也可读作a的n次幂
定义
如:在 中,底数是( )
指数是( )
读作( )
9
4
9的4次方
或9的4次幂
呢?
底数是( )
指数是( )
读作( )
-2
5
-2的5次方
或-2的5次幂
思考1
请指出下列各组数的异同。
当乘方的底数是负数或分数时,要加括号。
思考2
注意:
1)在 中,12是 数,10是
数,读作 ;
2) 的底数是 ,指数是 ,读作 ;
7
的7次方
底
指
12的10次方
练习1
3)在 中,-3是 数,16是 数,读作 ; 4)在 中,底数是 ;指数是 ;读作 ;
底
指
-3的16次方
17
的17次方
练习1
5)5看成幂的话,底数是 ,指数是 ,可读作 ; 6) 看成幂的话,底数是 ,指数是 ,可读作 ;
幂
指数
底数
5
1
5的一次方
1
的一次方
幂
指数
底数
一个数可以看成是这个数本身的一次方,指数1通常省略不写。
练习1
一、根据乘方的意义,把下列乘法式子写成
乘方的形式:
1、1×1×1×1×1×1×1= ;
2、3×3×3×3×3= ;
3、(-3)×(-3)×(-3)×(-3) = ;
4、
=
。
练习2
二、根据乘方的意义,把下列乘方写成乘法的形式:
1、 = ;
2、 = ;
3、 = 。
思考:用乘方式子怎么表示 的相反数?
练习2
判断下列各题是否正确:
( )① ;
( )② ;
( )③ ;
( )④ ;
对
错
错
错
练习3
例1、根据乘方的意义计算
例题讲解
负数的奇次幂是___数
负数的偶次幂是___数。
得出:
正
负
9
-32
1
抢答
正数的奇次幂是什么数?
0的任何正整数次幂都是0。
正数的任何次幂都是正数;
0呢?
正数的偶次幂是什么数?
思考
0的任何正整数次幂都是0。
负数的奇次幂是负数;
负数的偶次幂是正数;
正数的任何次幂都是正数;
归纳
确定下列幂的正负
+
-
+
+
-
抢答
(1) (2)
(3) (4)
(5) (6)
=1
=1
=-1
=1
=1
=-1
抢答
2、-1的幂很有规律:
-1的奇次幂是-1 ,
-1的偶次幂是1
1、1的任何次幂都为1
归纳
(1) (2)
(3) (4)
练习3
计算:
计算:(7~8选做)
1、 = ; 2、 = ;
3、 = ; 4、 = ;
5、 = ; 6、 = ;
7、 = ; 8、 = .
1
-1
25
-0.001
1
-27
-1
练习4
1.有理数的乘方的意义和相关概念;
2.乘方的有关运算;
4.体会特殊到一般,具体到抽象的数学方法。
幂的底数是分数或负数时,底数应该添上括号.
3.乘方的有关性质;
小结
1、在 中,底数是 ,指数 ,
2、 读做 ;
3、 的结果是 数(填“正”或“负”);
4、计算: = ;
5、计算: = ;
附加题:计算 。
4
6
-4的7次方或-4的7次幂
负
-8
0
检测
细胞分裂示意图
1个细胞30分钟后分裂成2个,经过5小时,这种细胞由1个能分裂成多少个?
2
2×2
2×2×2
2×2×·······×2×2
=
10个2
1个30ˊ
3个30ˊ
2个30ˊ
应用
乘方的故事
有一个长工到财主家去做工,他和财主商定:“第一天给一分钱,第二天给两分钱,以后每天是前一天的2倍.”财主答应了,到月底(30天)后,你猜一猜:财主会给长工多少工钱?
月底,长工兴冲冲的去领钱,他以为自己一下子可以领到一笔天文财富,结果财主只给了长工5分钱,而且还说是多给了他.
你知道这是怎么回事吗
拓展
长工算法:第一天1分,第二天2分,第三天4分,第四天16分,第五天256分……
财主算法:第一天0.01元,第二天0.02元,第三天0.0004元,第四天0.00000016元……
分 析
拓展
小珊有如下图所示的若干个棱长为1的正方体积木,要把它们用胶水粘在一起组成新的正方体.
数学活动2: 搭积木
拓展
第2次小珊用了8块积木;
第3次小珊用了27块积木;
照此规律继续下去,第10次小珊用了多少块积木?
第1次小珊用了1块积木;
拓展
你相信吗?
把一张厚为0.1毫米的纸折叠27次后,它
的厚度相当于1.5个珠穆朗玛峰的高度.
拓展
分析
有一张厚度是0.1毫米的纸,将它对折1次,厚度为2×0.1毫米.对折2次后,厚度为多少毫米?对折3次呢?4次呢?对折27次后,厚度为多少米?
227×0.1毫米= 13 421 772.8 毫米
=
13 421.7728
米
珠穆朗玛峰高为8 844米,这张纸对折27次后相当于1.5个珠穆朗玛峰那么高!
≈13 422米
拓展
盘锦四完中:马英欣
(1)边长为2cm的正方形的面积如何表示?
(2)棱长为2cm的正方体的体积如何表示?
读作:2的平方(2的二次方)
读作:2的立方(2的三次方)
2×2记作
2
2×2×2记作2
3
(1)2×2=4(cm2)
(2)2×2×2=8(cm3)
思考
这两个算式的共同点是什么?
2×2和2×2×2都是相同因数的乘法
为了简便
活动1
(1)边长为a的正方形的面积如何表示?
(2)棱长为a的正方体的体积如何表示?
记作
记作
读作:a的平方(a的二次方)
读作:a的立方(a的三次方)
4个a相乘呢?
5个a相乘呢?
100个a相乘呢?
活动2
猜一猜
(-2)× (-2)× (-2)×(-2)
记作:
读作:
(-
)
(-
)
(-
)
(-
)
(-
)
记作:
读作:
一般地,n个相同的因数a 相乘,即
记作: 。
(-2)4
-2的四次方
(- )
2
5
5
(- )
2
5
的五次方
读作:a的n次方
求n个相同因数的积的运算,叫做乘方。
乘方的结果叫做幂。
定义
指数
底数
幂
当 看作 的结果时,也可读作a的n次幂
定义
如:在 中,底数是( )
指数是( )
读作( )
9
4
9的4次方
或9的4次幂
呢?
底数是( )
指数是( )
读作( )
-2
5
-2的5次方
或-2的5次幂
思考1
请指出下列各组数的异同。
当乘方的底数是负数或分数时,要加括号。
思考2
注意:
1)在 中,12是 数,10是
数,读作 ;
2) 的底数是 ,指数是 ,读作 ;
7
的7次方
底
指
12的10次方
练习1
3)在 中,-3是 数,16是 数,读作 ; 4)在 中,底数是 ;指数是 ;读作 ;
底
指
-3的16次方
17
的17次方
练习1
5)5看成幂的话,底数是 ,指数是 ,可读作 ; 6) 看成幂的话,底数是 ,指数是 ,可读作 ;
幂
指数
底数
5
1
5的一次方
1
的一次方
幂
指数
底数
一个数可以看成是这个数本身的一次方,指数1通常省略不写。
练习1
一、根据乘方的意义,把下列乘法式子写成
乘方的形式:
1、1×1×1×1×1×1×1= ;
2、3×3×3×3×3= ;
3、(-3)×(-3)×(-3)×(-3) = ;
4、
=
。
练习2
二、根据乘方的意义,把下列乘方写成乘法的形式:
1、 = ;
2、 = ;
3、 = 。
思考:用乘方式子怎么表示 的相反数?
练习2
判断下列各题是否正确:
( )① ;
( )② ;
( )③ ;
( )④ ;
对
错
错
错
练习3
例1、根据乘方的意义计算
例题讲解
负数的奇次幂是___数
负数的偶次幂是___数。
得出:
正
负
9
-32
1
抢答
正数的奇次幂是什么数?
0的任何正整数次幂都是0。
正数的任何次幂都是正数;
0呢?
正数的偶次幂是什么数?
思考
0的任何正整数次幂都是0。
负数的奇次幂是负数;
负数的偶次幂是正数;
正数的任何次幂都是正数;
归纳
确定下列幂的正负
+
-
+
+
-
抢答
(1) (2)
(3) (4)
(5) (6)
=1
=1
=-1
=1
=1
=-1
抢答
2、-1的幂很有规律:
-1的奇次幂是-1 ,
-1的偶次幂是1
1、1的任何次幂都为1
归纳
(1) (2)
(3) (4)
练习3
计算:
计算:(7~8选做)
1、 = ; 2、 = ;
3、 = ; 4、 = ;
5、 = ; 6、 = ;
7、 = ; 8、 = .
1
-1
25
-0.001
1
-27
-1
练习4
1.有理数的乘方的意义和相关概念;
2.乘方的有关运算;
4.体会特殊到一般,具体到抽象的数学方法。
幂的底数是分数或负数时,底数应该添上括号.
3.乘方的有关性质;
小结
1、在 中,底数是 ,指数 ,
2、 读做 ;
3、 的结果是 数(填“正”或“负”);
4、计算: = ;
5、计算: = ;
附加题:计算 。
4
6
-4的7次方或-4的7次幂
负
-8
0
检测
细胞分裂示意图
1个细胞30分钟后分裂成2个,经过5小时,这种细胞由1个能分裂成多少个?
2
2×2
2×2×2
2×2×·······×2×2
=
10个2
1个30ˊ
3个30ˊ
2个30ˊ
应用
乘方的故事
有一个长工到财主家去做工,他和财主商定:“第一天给一分钱,第二天给两分钱,以后每天是前一天的2倍.”财主答应了,到月底(30天)后,你猜一猜:财主会给长工多少工钱?
月底,长工兴冲冲的去领钱,他以为自己一下子可以领到一笔天文财富,结果财主只给了长工5分钱,而且还说是多给了他.
你知道这是怎么回事吗
拓展
长工算法:第一天1分,第二天2分,第三天4分,第四天16分,第五天256分……
财主算法:第一天0.01元,第二天0.02元,第三天0.0004元,第四天0.00000016元……
分 析
拓展
小珊有如下图所示的若干个棱长为1的正方体积木,要把它们用胶水粘在一起组成新的正方体.
数学活动2: 搭积木
拓展
第2次小珊用了8块积木;
第3次小珊用了27块积木;
照此规律继续下去,第10次小珊用了多少块积木?
第1次小珊用了1块积木;
拓展
你相信吗?
把一张厚为0.1毫米的纸折叠27次后,它
的厚度相当于1.5个珠穆朗玛峰的高度.
拓展
分析
有一张厚度是0.1毫米的纸,将它对折1次,厚度为2×0.1毫米.对折2次后,厚度为多少毫米?对折3次呢?4次呢?对折27次后,厚度为多少米?
227×0.1毫米= 13 421 772.8 毫米
=
13 421.7728
米
珠穆朗玛峰高为8 844米,这张纸对折27次后相当于1.5个珠穆朗玛峰那么高!
≈13 422米
拓展
