1.2.2数轴
图片预览





文档简介
(共19张PPT)
第1.2.2 数轴
安徽省巢湖市中垾初中
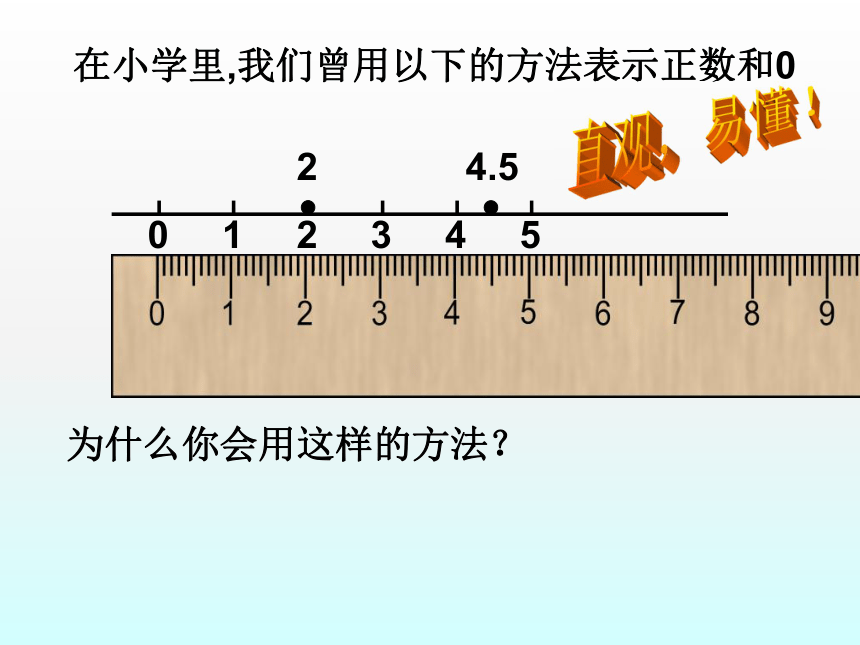
在小学里,我们曾用以下的方法表示正数和0
0 1 2 3 4 5
2
4.5
为什么你会用这样的方法?
-3.5
1
-0.5
4.5
-5
-2
0
3
5|2
七年级 数学
多媒体课件
在一条东西向的马路上,有一个汽车站,汽车站东3m和7.5m处分别有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一情境.
引入
3
7.5
-3
-4.8
东
西
汽车站
柳树
杨树
槐树
电线杆
0
怎样用数简明地表示这些树、电线杆与汽车站的相对位置关系 (方向、距离)
思 考
?
情境(2)
你会读温度计吗?
探究
1、上面两个问题有什么共同点?
2、你从中受到了什么启发?
3、你能用一条直线上的点来表示有理数吗?
归纳:情境1和情境2的共同点:
一般地,在数学中人们用画图的方式把数“直观化”.
这种直线叫数轴
通常用一条直线上的点表示数.
+
-
1.数轴的概念
规定了原点、正方向和单位长度的直线叫做数轴
直线
0
1
-2
-1
2
4
3
-3
学习数轴概念:一般地,在数学中人们用画图把数“直观化”。通常用一条直线上的点表示数,这条直线叫做数轴.
教师讲解、学生理解
(1)在直线上任取一个点表示数0,这个点叫做原点;
(2)通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;
(3)选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3,…;从原点向左,用类似方法表示-1,-2,-3,…
0
正方向
1
2
3
-1
-2
-3
例1.判断下面哪些是数轴,哪些不是 为什么
0
-2 -1 0 1 2
1 2 3 4
-2 0 1 2
-1 -2 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
※思考:你认为数轴最重要的哪三点?
正方向
数轴的三要素
单位长度
原点
画数轴时要注意以下四点:
⒈画直线.
⒉在直线上取一点作为原点.
⒊确定正方向,并用箭头表示.
⒋根据需要选取适当单位长度.
画数轴要体现出数轴的三要素:原点、正方向、长度单位.所有的有理数都可以用数轴的点表示出来.
1、画数轴
0
1
2
3
-1
-2
-3
4
-4
3.5
2、丰富数轴的内涵:分数或小数也可以用数轴上的点来表示,例如从原点向右3.5个单位长度的点表示小数3.5,从原点向左 个单位长度的点表示分数
2
3
-
3、问题:在数轴上能否实际画出表示一千万分之一的点?这个点存在吗?
不能
这个点存在
1、观察数轴上的点的特点:数轴上表示数3的点在原点的右边,与原点的距离是3个单位长度;表示数-2的点在原点的左边,与原点的距离是2个单位长度.
0
1
2
3
-1
-2
-3
4
-4
一般地,设a是一个正数,则数轴上表示数a的点在原点的______边,与原点的距离是______个单位长度;表示数-a的点在原点的______边,与原点的距离是______个单位长度.
右
a
左
a
例题1
(1)画 出数轴并表示下列有理数:
(2)写出数轴上点A、B、C、D、E表示的数:
0
1
2
3
-1
-2
-3
4
-4
1.5
-2
2
-2.5
0
0
1
2
3
-1
-2
-3
4
-4
E
A
B
C
D
点A表示0
点B表示-2
点C表示1
点D表示2.5
点E表示-3
多媒体课件
0
1
2
3
解:
练习
画出数轴,并用数轴上的点表示下列各数:
3|2
-5,0,5,-4,
-
3|2
,
4
5
-5
-4
-3
-2
-1
-
3|2
3|2
如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动4个单位长度,可以看出,终点表示的数是-1,已知A、B是数轴上的点,请参照下图,完成填空。
-5 -4 -3 -2 -1 0 1 2 3 4 5
(1)若点A表示-3,把A向右移动7个单位长度,则终点表示的数是 。
(2)若点A表示3,把A向左移动7个单位长度,再向右移动的4个单位长度,则终点表示的数是 。
(3)若把点B向右移动3个单位长度,再向左移动4个单位长度,终点表示的数是0,则点B所表示的数是 。
.如图,点A与点B的距离是3个单位长度的木条,当木条左端A点落在-9与-8之间,B点落在哪两个整数之间?
-5 -4 -3 -2 -1 0 1 2 3 4 5
.如图,以P点为圆心,3个单位长度为半径画圆,该圆与数轴交点表示的数是多少?
-5 -4 -3 -2 -1 0 1 2 3 4 5
P
(1)数轴概念:一般地,在数学中人们用画图把数“直观化”.通常用一条直线上的点表示数,这条直线叫做数轴.
(2)数轴的三要素:原点、正方向、长度单位
(3)数与形的关系:一 一对应的关系.
(4)数学思想:数形结合的思想.
第1.2.2 数轴
安徽省巢湖市中垾初中
在小学里,我们曾用以下的方法表示正数和0
0 1 2 3 4 5
2
4.5
为什么你会用这样的方法?
-3.5
1
-0.5
4.5
-5
-2
0
3
5|2
七年级 数学
多媒体课件
在一条东西向的马路上,有一个汽车站,汽车站东3m和7.5m处分别有一棵柳树和一棵杨树,汽车站西3m和4.8m处分别有一棵槐树和一根电线杆,试画图表示这一情境.
引入
3
7.5
-3
-4.8
东
西
汽车站
柳树
杨树
槐树
电线杆
0
怎样用数简明地表示这些树、电线杆与汽车站的相对位置关系 (方向、距离)
思 考
?
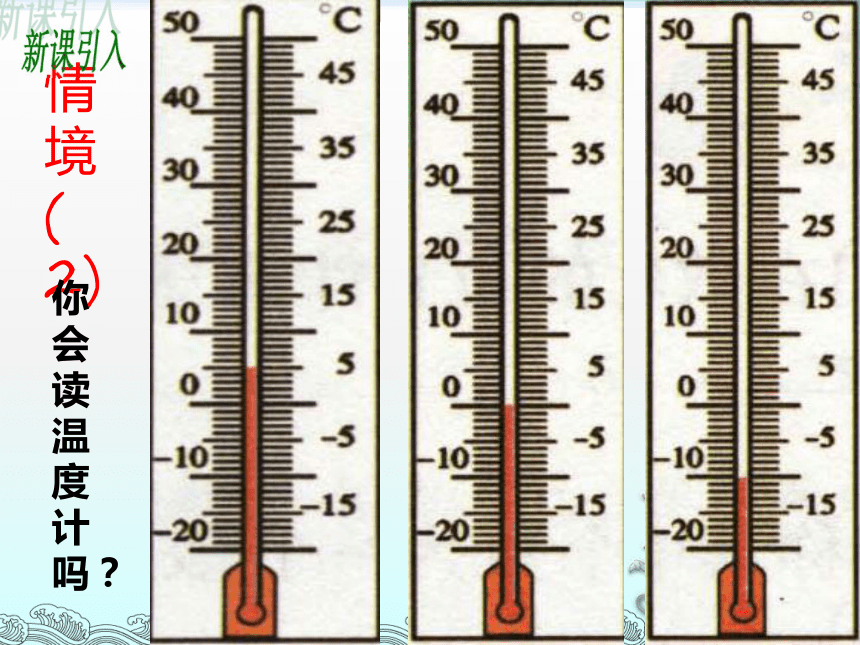
情境(2)
你会读温度计吗?
探究
1、上面两个问题有什么共同点?
2、你从中受到了什么启发?
3、你能用一条直线上的点来表示有理数吗?
归纳:情境1和情境2的共同点:
一般地,在数学中人们用画图的方式把数“直观化”.
这种直线叫数轴
通常用一条直线上的点表示数.
+
-
1.数轴的概念
规定了原点、正方向和单位长度的直线叫做数轴
直线
0
1
-2
-1
2
4
3
-3
学习数轴概念:一般地,在数学中人们用画图把数“直观化”。通常用一条直线上的点表示数,这条直线叫做数轴.
教师讲解、学生理解
(1)在直线上任取一个点表示数0,这个点叫做原点;
(2)通常规定直线上从原点向右(或上)为正方向,从原点向左(或下)为负方向;
(3)选取适当的长度为单位长度,直线上从原点向右,每隔一个单位长度取一个点,依次表示1,2,3,…;从原点向左,用类似方法表示-1,-2,-3,…
0
正方向
1
2
3
-1
-2
-3
例1.判断下面哪些是数轴,哪些不是 为什么
0
-2 -1 0 1 2
1 2 3 4
-2 0 1 2
-1 -2 0 1 2
-2 -1 0 1 2
-2 -1 0 1 2
※思考:你认为数轴最重要的哪三点?
正方向
数轴的三要素
单位长度
原点
画数轴时要注意以下四点:
⒈画直线.
⒉在直线上取一点作为原点.
⒊确定正方向,并用箭头表示.
⒋根据需要选取适当单位长度.
画数轴要体现出数轴的三要素:原点、正方向、长度单位.所有的有理数都可以用数轴的点表示出来.
1、画数轴
0
1
2
3
-1
-2
-3
4
-4
3.5
2、丰富数轴的内涵:分数或小数也可以用数轴上的点来表示,例如从原点向右3.5个单位长度的点表示小数3.5,从原点向左 个单位长度的点表示分数
2
3
-
3、问题:在数轴上能否实际画出表示一千万分之一的点?这个点存在吗?
不能
这个点存在
1、观察数轴上的点的特点:数轴上表示数3的点在原点的右边,与原点的距离是3个单位长度;表示数-2的点在原点的左边,与原点的距离是2个单位长度.
0
1
2
3
-1
-2
-3
4
-4
一般地,设a是一个正数,则数轴上表示数a的点在原点的______边,与原点的距离是______个单位长度;表示数-a的点在原点的______边,与原点的距离是______个单位长度.
右
a
左
a
例题1
(1)画 出数轴并表示下列有理数:
(2)写出数轴上点A、B、C、D、E表示的数:
0
1
2
3
-1
-2
-3
4
-4
1.5
-2
2
-2.5
0
0
1
2
3
-1
-2
-3
4
-4
E
A
B
C
D
点A表示0
点B表示-2
点C表示1
点D表示2.5
点E表示-3
多媒体课件
0
1
2
3
解:
练习
画出数轴,并用数轴上的点表示下列各数:
3|2
-5,0,5,-4,
-
3|2
,
4
5
-5
-4
-3
-2
-1
-
3|2
3|2
如图,一个点从数轴上的原点开始,先向右移动3个单位长度,再向左移动4个单位长度,可以看出,终点表示的数是-1,已知A、B是数轴上的点,请参照下图,完成填空。
-5 -4 -3 -2 -1 0 1 2 3 4 5
(1)若点A表示-3,把A向右移动7个单位长度,则终点表示的数是 。
(2)若点A表示3,把A向左移动7个单位长度,再向右移动的4个单位长度,则终点表示的数是 。
(3)若把点B向右移动3个单位长度,再向左移动4个单位长度,终点表示的数是0,则点B所表示的数是 。
.如图,点A与点B的距离是3个单位长度的木条,当木条左端A点落在-9与-8之间,B点落在哪两个整数之间?
-5 -4 -3 -2 -1 0 1 2 3 4 5
.如图,以P点为圆心,3个单位长度为半径画圆,该圆与数轴交点表示的数是多少?
-5 -4 -3 -2 -1 0 1 2 3 4 5
P
(1)数轴概念:一般地,在数学中人们用画图把数“直观化”.通常用一条直线上的点表示数,这条直线叫做数轴.
(2)数轴的三要素:原点、正方向、长度单位
(3)数与形的关系:一 一对应的关系.
(4)数学思想:数形结合的思想.
