贵州省沧江中学2013届高三上学期8月月考数学(文)试题
文档属性
| 名称 | 贵州省沧江中学2013届高三上学期8月月考数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 134.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-25 08:20:47 | ||
图片预览



文档简介
贵州省沧江中学2013届高三上学期8月月考文科数学试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合;,则中所含元素
的个数为 ( )
A. B. C. D.
【答案】D
2.已知f(x)在R上是奇函数,f(x+4)=f(x),当x∈(0,2)时,f(x)=2x2,则f(7)=( ).
A.-2 B.2 C.-98 D.98
【答案】A
3.已知集合A={x|x2-x-2<0},B={x|-1A.A?B B.B?A
C.A=B D.A∩B=
【答案】B
4.函数的大致图象为( )
【答案】D
5.若函数为偶函数,且在上是减函数,又,则的解集为 ( )
A.(-3,3) B.
C. D.
【答案】C
6. 设函数,若,则的取值范围是 ( )
A. B.
C. D.
【答案】B
7.设是定义在R上的奇函数,且当时单调递减,若,则的值 ( )
A.恒为负值 B.恒等于零 C.恒为正值 D.无法确定正负
【答案】A
8.设,则等于( )
A. B. C. D.
【答案】D
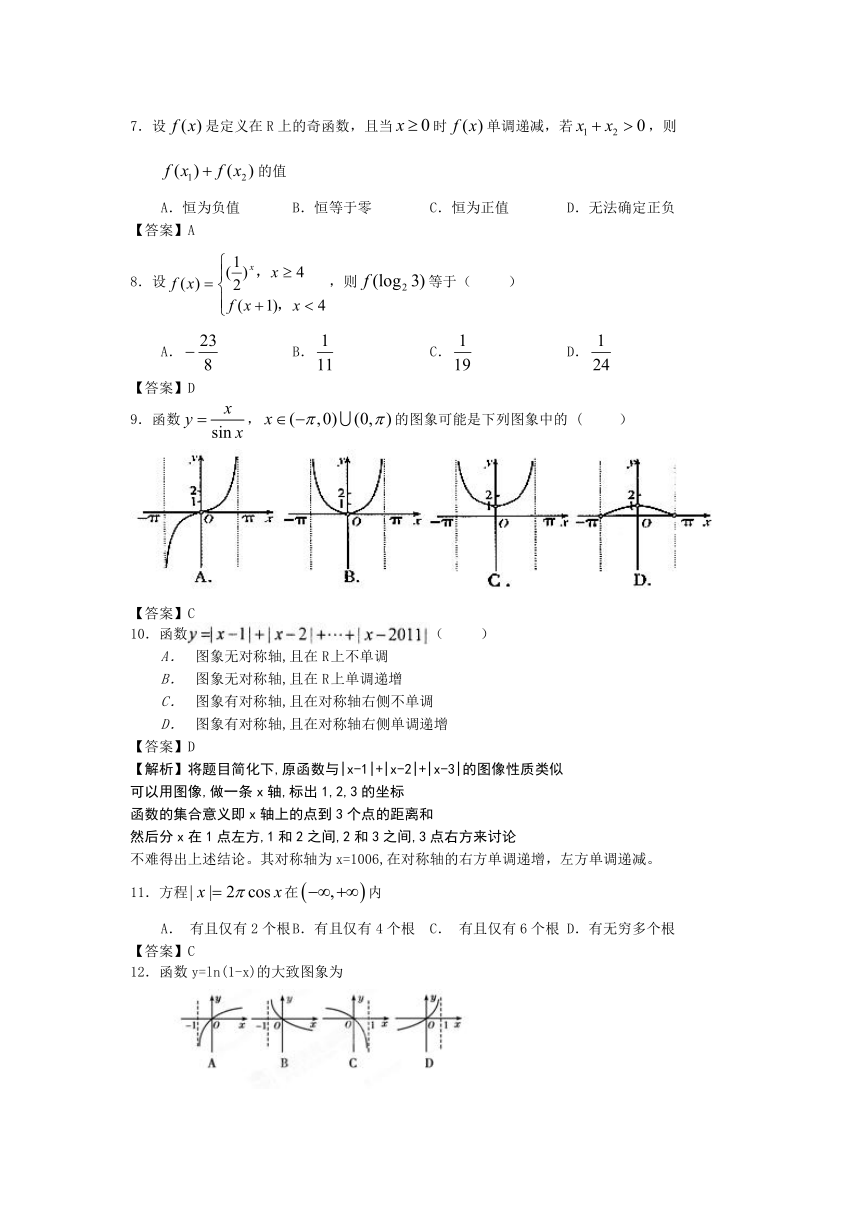
9.函数,的图象可能是下列图象中的 ( )
【答案】C
10.函数( )
A. 图象无对称轴,且在R上不单调
B. 图象无对称轴,且在R上单调递增
C. 图象有对称轴,且在对称轴右侧不单调
D. 图象有对称轴,且在对称轴右侧单调递增
【答案】D
【解析】将题目简化下,原函数与|x-1|+|x-2|+|x-3|的图像性质类似
可以用图像,做一条x轴,标出1,2,3的坐标
函数的集合意义即x轴上的点到3个点的距离和
然后分x在1点左方,1和2之间,2和3之间,3点右方来讨论
不难得出上述结论。其对称轴为x=1006,在对称轴的右方单调递增,左方单调递减。
11.方程在内
A. 有且仅有2个根 B.有且仅有4个根 C. 有且仅有6个根 D.有无穷多个根
【答案】C
12.函数y=ln(1-x)的大致图象为 ( )
【答案】C
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.集合,若的子集有4个,则的取值范围是 .
【答案】
14.已知函数若,则 .
【答案】或-1
15.已知,则 。
【答案】24
16. 已知函数,对于下列命题:
①若,则; ②若,则;
③,则; ④.
其中正确的命题的序号是 (写出所有正确命题的序号).
【答案】①②
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.已知集合A={x||x-1|<2},B={x|x2+ax-6<0},C={x|x2-2x-15<0}.
(1)若A∪B=B,求a的取值范围;
(2)是否存在a的值使得A∪B=B∩C?若存在,求出a的值;若不存在,请说明理由.
【答案】 A={x|-1(1)由A∪B=B知,A B,令f(x)=x2+ax-6,则
解得-5≤a≤-1,即a的取值范围是[-5,-1].
(2)假设存在a的值使得A∪B=B∩C,由A∪B=B∩C B知A B,
由A∪B=B∩C C知B C,于是A B C,
由(1)知若A B,则a∈[-5,-1],
当B C时,由Δ=a2+24>0,知B不可能是空集,
于是
解得a∈,
综合a∈[-5,-1]知存在a∈满足条件.
18.如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
(Ⅰ)设AD=x(x0),ED=y,求用x表示y的函数关系式,并
注明函数的定义域;
(Ⅱ)如果DE是灌溉水管,为节约成本,希望它最短,DE的位
置应在哪里?
如果DE是参观线路,则希望它最长,DE的位置又应在哪里?
请给予证明.
【答案】(Ⅰ)在△ADE中,由余弦定理得:
,
又.
把代入得,
∴
∵ ∴
即函数的定义域为.
(Ⅱ)如果DE是水管,则,
当且仅当,即时“=”成立,故DEBC,且DE=.
如果DE是参观线路,记,则
∴函数在上递减,在上递增
故.
∴.
即DE为AB中线或AC中线时,DE最长.
19.已知且,求使方程有解时的的取值范围
【答案】
,即①,或②
当时,①得,与矛盾;②不成立
当时,①得,恒成立,即;②不成立
显然,当时,①得,不成立,
②得得
∴或
20.某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
【答案】(1)当每辆车月租金为3600元时,未租出的车辆数为 =12,所以这时租出了88辆.
(2)设每辆车的月租金定为x元,则公司月收益为
f(x)=(100-)(x-150)-×50
整理得:f(x)=-+162x-2100=-(x-4050)2+307050
∴当x=4050时,f(x)最大,最大值为f(4050)=307050 元
21.设关于的方程
(Ⅰ)若方程有实数解,求实数的取值范围;
(Ⅱ)当方程有实数解时,讨论方程实根的个数,并求出方程的解.
【答案】(Ⅰ)原方程为,
,
时方程有实数解;
(Ⅱ)①当时,,∴方程有唯一解;
②当时,.
的解为;
令
的解为;
综合①.②,得
1)当时原方程有两解:;
2)当时,原方程有唯一解;
22.设是定义在上的函数,且对任意,当时,都有;
(1)当时,比较的大小;(2)解不等式;
(3)设且,求的取值范围。
【答案】(1)由对任意,当时,都有可得: 在上为单调增函数,因为,所以, .
(2)由题意及(1)得:解得,所以不等式
的解集为
(3)由题意得: 即:
又因为,所以,
所以,的取值范围是
解析:通过是定义在上的函数,且对任意,当时,都有考查对函数单调性定义的理解,通过解不等式考查函数单调性的转化,通过 且考查对函数定义域问题的转化以及求集合的交的运算以及分类讨论,属于中档题.
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合;,则中所含元素
的个数为 ( )
A. B. C. D.
【答案】D
2.已知f(x)在R上是奇函数,f(x+4)=f(x),当x∈(0,2)时,f(x)=2x2,则f(7)=( ).
A.-2 B.2 C.-98 D.98
【答案】A
3.已知集合A={x|x2-x-2<0},B={x|-1
C.A=B D.A∩B=
【答案】B
4.函数的大致图象为( )
【答案】D
5.若函数为偶函数,且在上是减函数,又,则的解集为 ( )
A.(-3,3) B.
C. D.
【答案】C
6. 设函数,若,则的取值范围是 ( )
A. B.
C. D.
【答案】B
7.设是定义在R上的奇函数,且当时单调递减,若,则的值 ( )
A.恒为负值 B.恒等于零 C.恒为正值 D.无法确定正负
【答案】A
8.设,则等于( )
A. B. C. D.
【答案】D
9.函数,的图象可能是下列图象中的 ( )
【答案】C
10.函数( )
A. 图象无对称轴,且在R上不单调
B. 图象无对称轴,且在R上单调递增
C. 图象有对称轴,且在对称轴右侧不单调
D. 图象有对称轴,且在对称轴右侧单调递增
【答案】D
【解析】将题目简化下,原函数与|x-1|+|x-2|+|x-3|的图像性质类似
可以用图像,做一条x轴,标出1,2,3的坐标
函数的集合意义即x轴上的点到3个点的距离和
然后分x在1点左方,1和2之间,2和3之间,3点右方来讨论
不难得出上述结论。其对称轴为x=1006,在对称轴的右方单调递增,左方单调递减。
11.方程在内
A. 有且仅有2个根 B.有且仅有4个根 C. 有且仅有6个根 D.有无穷多个根
【答案】C
12.函数y=ln(1-x)的大致图象为 ( )
【答案】C
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.集合,若的子集有4个,则的取值范围是 .
【答案】
14.已知函数若,则 .
【答案】或-1
15.已知,则 。
【答案】24
16. 已知函数,对于下列命题:
①若,则; ②若,则;
③,则; ④.
其中正确的命题的序号是 (写出所有正确命题的序号).
【答案】①②
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.已知集合A={x||x-1|<2},B={x|x2+ax-6<0},C={x|x2-2x-15<0}.
(1)若A∪B=B,求a的取值范围;
(2)是否存在a的值使得A∪B=B∩C?若存在,求出a的值;若不存在,请说明理由.
【答案】 A={x|-1
解得-5≤a≤-1,即a的取值范围是[-5,-1].
(2)假设存在a的值使得A∪B=B∩C,由A∪B=B∩C B知A B,
由A∪B=B∩C C知B C,于是A B C,
由(1)知若A B,则a∈[-5,-1],
当B C时,由Δ=a2+24>0,知B不可能是空集,
于是
解得a∈,
综合a∈[-5,-1]知存在a∈满足条件.
18.如图,公园有一块边长为2的等边△ABC的边角地,现修成草坪,图中DE把草坪分成面积相等的两部分,D在AB上,E在AC上.
(Ⅰ)设AD=x(x0),ED=y,求用x表示y的函数关系式,并
注明函数的定义域;
(Ⅱ)如果DE是灌溉水管,为节约成本,希望它最短,DE的位
置应在哪里?
如果DE是参观线路,则希望它最长,DE的位置又应在哪里?
请给予证明.
【答案】(Ⅰ)在△ADE中,由余弦定理得:
,
又.
把代入得,
∴
∵ ∴
即函数的定义域为.
(Ⅱ)如果DE是水管,则,
当且仅当,即时“=”成立,故DEBC,且DE=.
如果DE是参观线路,记,则
∴函数在上递减,在上递增
故.
∴.
即DE为AB中线或AC中线时,DE最长.
19.已知且,求使方程有解时的的取值范围
【答案】
,即①,或②
当时,①得,与矛盾;②不成立
当时,①得,恒成立,即;②不成立
显然,当时,①得,不成立,
②得得
∴或
20.某租赁公司拥有汽车100辆,当每辆车的月租金为3000元时,可全部租出,当每辆车的月租金每增加50元时,未租出的车将会增加一辆,租出的车每辆每月需维护费150元,未租出的车每辆每月需要维护费50元.
(1)当每辆车的月租金定为3600元时,能租出多少辆车?
(2)当每辆车的月租金定为多少元时,租赁公司的月收益最大?最大月收益是多少?
【答案】(1)当每辆车月租金为3600元时,未租出的车辆数为 =12,所以这时租出了88辆.
(2)设每辆车的月租金定为x元,则公司月收益为
f(x)=(100-)(x-150)-×50
整理得:f(x)=-+162x-2100=-(x-4050)2+307050
∴当x=4050时,f(x)最大,最大值为f(4050)=307050 元
21.设关于的方程
(Ⅰ)若方程有实数解,求实数的取值范围;
(Ⅱ)当方程有实数解时,讨论方程实根的个数,并求出方程的解.
【答案】(Ⅰ)原方程为,
,
时方程有实数解;
(Ⅱ)①当时,,∴方程有唯一解;
②当时,.
的解为;
令
的解为;
综合①.②,得
1)当时原方程有两解:;
2)当时,原方程有唯一解;
22.设是定义在上的函数,且对任意,当时,都有;
(1)当时,比较的大小;(2)解不等式;
(3)设且,求的取值范围。
【答案】(1)由对任意,当时,都有可得: 在上为单调增函数,因为,所以, .
(2)由题意及(1)得:解得,所以不等式
的解集为
(3)由题意得: 即:
又因为,所以,
所以,的取值范围是
解析:通过是定义在上的函数,且对任意,当时,都有考查对函数单调性定义的理解,通过解不等式考查函数单调性的转化,通过 且考查对函数定义域问题的转化以及求集合的交的运算以及分类讨论,属于中档题.
同课章节目录
