贵州省鲁屯中学2013届高三上学期8月月考数学(文)试题
文档属性
| 名称 | 贵州省鲁屯中学2013届高三上学期8月月考数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 113.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-25 08:23:03 | ||
图片预览


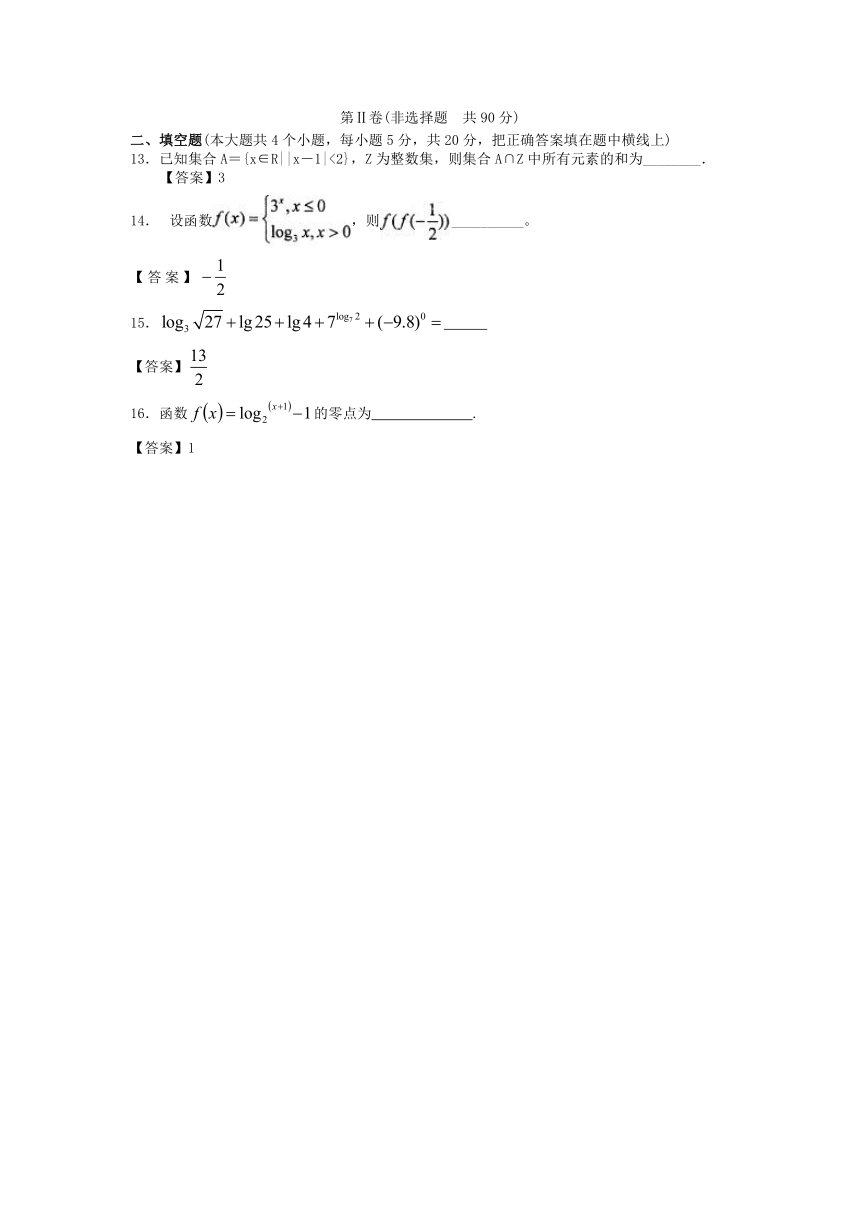
文档简介
贵州省鲁屯中学2013届高三上学期8月月考文科数学试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合M={x|},N={x|},则集合等于( )
A.{x|x<-2} B.{x|x>3}
C.{x|-1【答案】C
2.集合,,的真子集的个数为
A.6 B.7 C.8 D.9
【答案】B
3.奇函数在上的解析式是,则在上的函数解析式是( )
A. B.
C. D.
【答案】B
4.若点(a,b)在y=lgx图像上,a≠1,则下列点也在此图像上的是( )
A.(,b) B.(10a,1-b)
C.(,b+1) D.(a2,2b)
【答案】D
5. 定义在R上的函数满足:成立,且上单调递增,设,则a、b、c的大小关系是( )
A. B. C. D.
【答案】A
6.若,则 ( )
A. B. C. D.
【答案】C
7.已知函数,则方程(为正实数)的根的个数不可能为( )
A.3个 B.4个 C.5个 D.6个
【答案】A
8.若函数y=f(x)(x∈R)满足f(x+2)=f(x)且x∈(-1,1时f(x)=1-x2,函数g(x)=,则函数h(x)=f(x)-g(x)在区间-5,10内零点的个数为( )
A.14 B.13 C. 12 D.8
【答案】A
9. 如图,虚线部分是四个象限的角平分线,实线部分是函数的部分图象,则可能是( )
A. B.
C. D.
【答案】C
10.设函数 若是奇函数,则的值是( )
A. B. C. D. 4
【答案】A
11.幂函数的图象经过点,则的值为( )
A.1 B.2 C.3 D.4
【答案】B
12.函数的零点所在的一个区间是 ( )
A.(一2,一1) B.(一1,0) C.(0,1) D.(1,2)
【答案】B
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.已知集合A={x∈R||x-1|<2},Z为整数集,则集合A∩Z中所有元素的和为________.
【答案】3
14. 设函数,则__________。
【答案】
15.
【答案】
16.函数的零点为 .
【答案】1
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.A=,
B=
(1)求A,B
(2)求
【答案】 (1)A={x|018.已知函数(为常数).
(1)若常数且,求的定义域;
(2)若在区间(2,4)上是减函数,求的取值范围.
【答案】(1)由,当时,解得或,
当时,解得.
故当时,的定义域为{或}
当时,的定义域为}.
(2)令,因为为减函数,故要使在(2,4)上是减函数,
在(2,4)上为增且为正.
故有.
故.
19.当时,求函数的最小值。
【答案】对称轴
当,即时,是的递增区间,;
当,即时,是的递减区间,;
当,即时,。
20.提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度(单位:千米/小时)是车流密度(单位:辆/千米)的函数,当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明;当时,车流速度是车流密度的一次函数.
(Ⅰ)当时,求函数的表达式;
(Ⅱ)当车流密度为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)可以达到最大,并求最大值(精确到1辆/小时).
【答案】(1)由题意,当时,;当时,设
由已知,解得.
故函数的表达式为.
(2)由题意并由(1)可得
当时,为增函数,故当时,其最大值为;
当时,
当且仅当即时等号成立.
所以当时,在区间上取得最大值.
综上可知,当时, 在区间上取得最大值.
即当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时
21.提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度(单位:千米/小时)是车流密度(单位:辆/千米)的函数,当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明;当时,车流速度是车流密度的一次函数.
(Ⅰ)当时,求函数的表达式;
(Ⅱ)当车流密度为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)可以达到最大,并求最大值(精确到1辆/小时).
【答案】(1)由题意,当时,;当时,设
由已知,解得.
故函数的表达式为.
(2)由题意并由(1)可得
当时,为增函数,故当时,其最大值为;
当时,
当且仅当即时等号成立.
所以当时,在区间上取得最大值.
综上可知,当时, 在区间上取得最大值.
即当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时
22.某公司为了实现2011年1000万元的利润的目标,准备制定一个激励销售人员的奖励方案:销售利润达到10万元时,按销售利润进行奖励,且奖金数额y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金数额不超过5万元,同时奖金数额不超过利润的25%,现有二个奖励模型:,问其中是否有模型能完全符合公司的要求?说明理由。(解题提示:公司要求的模型只需满足:当时,①函数为增函数;②函数的最大值不超过5;③,参考数据:)
【答案】由题意,符合公司要求的模型只需满足:当时,
①函数为增函数;②函数的最大值不超过5 ; ③%.
(1)对于,易知满足①,但当时,,.
不满足公司要求;…(5分)
(2)对于 ,易知满足①,
当时,.
又,满足②
而%(1)
设
在为减函数.
(1)式成立,
满足③ .
综上,只有奖励模型:能完全符合公司的要求
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.已知集合M={x|},N={x|},则集合等于( )
A.{x|x<-2} B.{x|x>3}
C.{x|-1
2.集合,,的真子集的个数为
A.6 B.7 C.8 D.9
【答案】B
3.奇函数在上的解析式是,则在上的函数解析式是( )
A. B.
C. D.
【答案】B
4.若点(a,b)在y=lgx图像上,a≠1,则下列点也在此图像上的是( )
A.(,b) B.(10a,1-b)
C.(,b+1) D.(a2,2b)
【答案】D
5. 定义在R上的函数满足:成立,且上单调递增,设,则a、b、c的大小关系是( )
A. B. C. D.
【答案】A
6.若,则 ( )
A. B. C. D.
【答案】C
7.已知函数,则方程(为正实数)的根的个数不可能为( )
A.3个 B.4个 C.5个 D.6个
【答案】A
8.若函数y=f(x)(x∈R)满足f(x+2)=f(x)且x∈(-1,1时f(x)=1-x2,函数g(x)=,则函数h(x)=f(x)-g(x)在区间-5,10内零点的个数为( )
A.14 B.13 C. 12 D.8
【答案】A
9. 如图,虚线部分是四个象限的角平分线,实线部分是函数的部分图象,则可能是( )
A. B.
C. D.
【答案】C
10.设函数 若是奇函数,则的值是( )
A. B. C. D. 4
【答案】A
11.幂函数的图象经过点,则的值为( )
A.1 B.2 C.3 D.4
【答案】B
12.函数的零点所在的一个区间是 ( )
A.(一2,一1) B.(一1,0) C.(0,1) D.(1,2)
【答案】B
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.已知集合A={x∈R||x-1|<2},Z为整数集,则集合A∩Z中所有元素的和为________.
【答案】3
14. 设函数,则__________。
【答案】
15.
【答案】
16.函数的零点为 .
【答案】1
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.A=,
B=
(1)求A,B
(2)求
【答案】 (1)A={x|0
(1)若常数且,求的定义域;
(2)若在区间(2,4)上是减函数,求的取值范围.
【答案】(1)由,当时,解得或,
当时,解得.
故当时,的定义域为{或}
当时,的定义域为}.
(2)令,因为为减函数,故要使在(2,4)上是减函数,
在(2,4)上为增且为正.
故有.
故.
19.当时,求函数的最小值。
【答案】对称轴
当,即时,是的递增区间,;
当,即时,是的递减区间,;
当,即时,。
20.提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度(单位:千米/小时)是车流密度(单位:辆/千米)的函数,当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明;当时,车流速度是车流密度的一次函数.
(Ⅰ)当时,求函数的表达式;
(Ⅱ)当车流密度为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)可以达到最大,并求最大值(精确到1辆/小时).
【答案】(1)由题意,当时,;当时,设
由已知,解得.
故函数的表达式为.
(2)由题意并由(1)可得
当时,为增函数,故当时,其最大值为;
当时,
当且仅当即时等号成立.
所以当时,在区间上取得最大值.
综上可知,当时, 在区间上取得最大值.
即当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时
21.提高过江大桥的车辆通行能力可改善整个城市的交通状况.在一般情况下,大桥上的车流速度(单位:千米/小时)是车流密度(单位:辆/千米)的函数,当桥上的的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明;当时,车流速度是车流密度的一次函数.
(Ⅰ)当时,求函数的表达式;
(Ⅱ)当车流密度为多大时,车流量(单位时间内通过桥上某观点的车辆数,单位:辆/每小时)可以达到最大,并求最大值(精确到1辆/小时).
【答案】(1)由题意,当时,;当时,设
由已知,解得.
故函数的表达式为.
(2)由题意并由(1)可得
当时,为增函数,故当时,其最大值为;
当时,
当且仅当即时等号成立.
所以当时,在区间上取得最大值.
综上可知,当时, 在区间上取得最大值.
即当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时
22.某公司为了实现2011年1000万元的利润的目标,准备制定一个激励销售人员的奖励方案:销售利润达到10万元时,按销售利润进行奖励,且奖金数额y(单位:万元)随销售利润x(单位:万元)的增加而增加,但奖金数额不超过5万元,同时奖金数额不超过利润的25%,现有二个奖励模型:,问其中是否有模型能完全符合公司的要求?说明理由。(解题提示:公司要求的模型只需满足:当时,①函数为增函数;②函数的最大值不超过5;③,参考数据:)
【答案】由题意,符合公司要求的模型只需满足:当时,
①函数为增函数;②函数的最大值不超过5 ; ③%.
(1)对于,易知满足①,但当时,,.
不满足公司要求;…(5分)
(2)对于 ,易知满足①,
当时,.
又,满足②
而%(1)
设
在为减函数.
(1)式成立,
满足③ .
综上,只有奖励模型:能完全符合公司的要求
同课章节目录
