贵州省洛万中学2013届高三上学期8月月考数学(文)试题
文档属性
| 名称 | 贵州省洛万中学2013届高三上学期8月月考数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 401.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-25 08:24:23 | ||
图片预览



文档简介
贵州省洛万中学2013届高三上学期8月月考文科数学试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设集合A={x|1A.(1,4) B.(3,4)
C.(1,3) D.(1,2)∪(3,4)
【答案】B
2.已知集合则 ( )
A. B. C.{0, 2} D.{0,1, 2}
【答案】D
3.对于平面上的点集Ω,如果连接Ω中任意两点的线段必定包含于Ω,则称Ω为平面上的凸集,给出平面上4个点集的图形如图 (阴影区域及其边界),其中为凸集的是( )
A.①③ B.②③ C.③④ D.①④
【答案】B
4.函数f(x)=(a>0且a≠1)是R上的减函数,则a的取值范围是( )
A.(0,1) B.
C. D.
【答案】B
5. 设函数,若,则的取值范围是 ( )
A. B.
C. D.
【答案】B
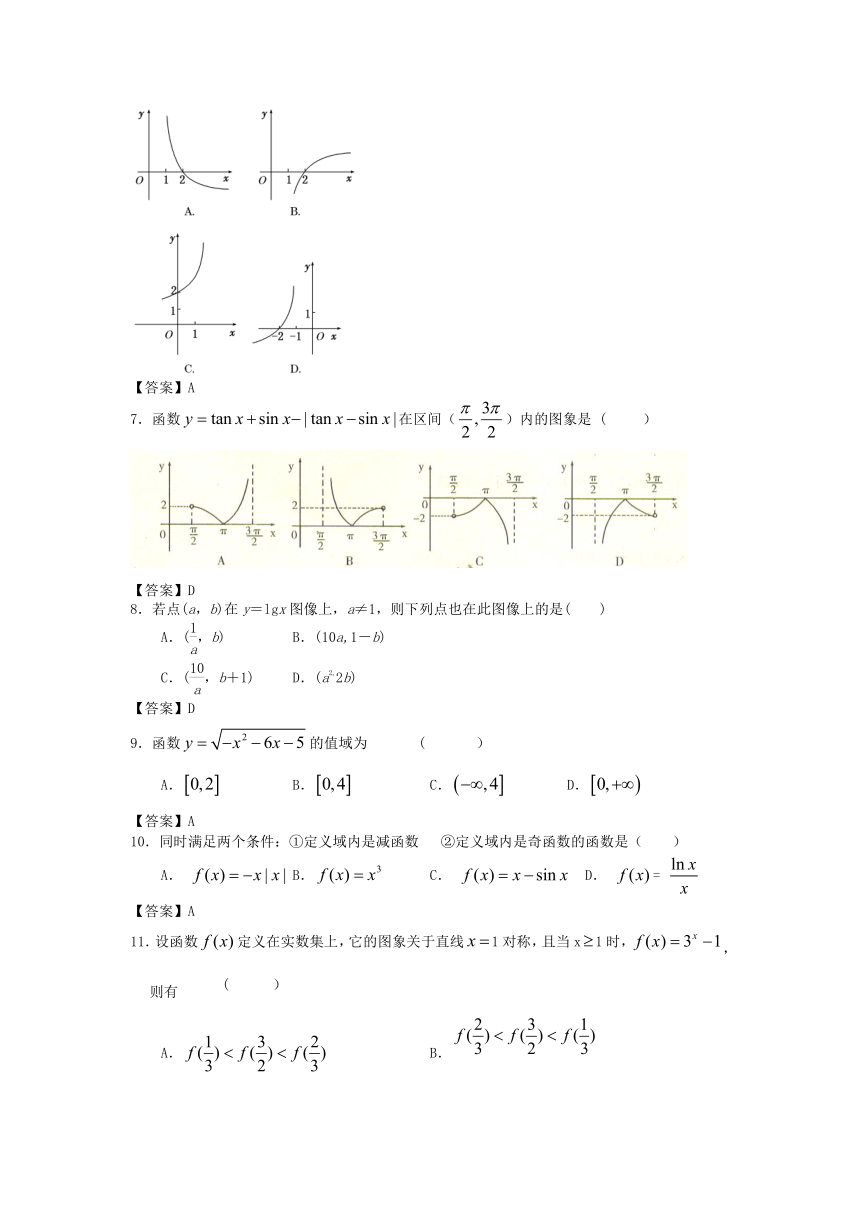
6.函数y=()x+1的图像关于直线y=x对称的图像大致是( )
【答案】A
7.函数在区间()内的图象是 ( )
【答案】D
8.若点(a,b)在y=lgx图像上,a≠1,则下列点也在此图像上的是( )
A.(,b) B.(10a,1-b)
C.(,b+1) D.(a2,2b)
【答案】D
9.函数的值域为 ( )
A. B. C. D.
【答案】A
10.同时满足两个条件:①定义域内是减函数 ②定义域内是奇函数的函数是( )
A. B. C. D. =
【答案】A
11.设函数定义在实数集上,它的图象关于直线1对称,且当x1时,,则有 ( )
A. B.
C. D.
【答案】B
12.,则 ( )
A. B. C. D.
【答案】C
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.已知全集,集合和的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合的元素共有 个.
【答案】2
14.函数关于直线x=1对称,则m=
【答案】
15.关于的不等式()的解集为 .
【答案】
16.定义在上的偶函数,对任意的均有成立,当时,,则直线与函数的图像交点中最近两点的距离等于 .
【答案】1
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.设集合A={(x,y)|y=2x-1,x∈N*},B={(x,y)|y=ax2-ax+a,x∈N*},问是否存在非零整数a,使A∩B≠ ?若存在,请求出a的值;若不存在,说明理由.
【答案】假设A∩B≠ ,则方程组
有正整数解,消去y得,
ax2-(a+2)x+a+1=0(*)
由Δ≥0,有(a+2)2-4a(a+1)≥0,
解得-≤a≤.
因a为非零整数,∴a=±1,
当a=-1时,代入(*),解得x=0或x=-1,
而x∈N*.故a≠-1.
当a=1时,代入(*),解得x=1或x=2,符合题意.
故存在a=1,使得A∩B≠ ,
此时A∩B={(1,1),(2,3)}.
18.已知奇函数f(x)在定义域[-2,2]上单调递减,求满足f(1-m)+f(1-m2)<0的实数m的取值范围.
【答案】由f(1-m)+f(1-m2)<0,
得f(1-m)<-f(1-m2).
又f(x)为奇函数,
∴f(1-m)又∵f(x)在[-2,2]上单调递减,
∴解得-1≤m<1.
∴实数m的取值范围为[-1,1).
19.已知函数与g(x)=m-x的图象有两个不同的交点,求实数m的取值范围.
【答案】与g(x)=m-x的图象如图.
由得x2-(2m-1)x+m2=0,
由Δ=(2m-1)2-4m2=0,
即f(x)与g(x)的图象恰有一个交点时,
依题意当0≤m时,
f(x)与g(x)的图象有两个不同的交点,
即实数m的取值范围是.
20.提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度(单位:千米/小时)是车流密度(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当时,车流速度是车流密度的一次函数.
(Ⅰ)当时,求函数的表达式;
(Ⅱ)当车流密度为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)可以达到最大,并求出最大值.(精确到1辆/小时)
【答案】(Ⅰ)由题意当时,;当时,设,
显然在是减函数,由已知得,
解得
故函数的表达式为=
(Ⅱ)依题意并由(Ⅰ)可得
当时,为增函数,故当时,其最大值为;
当时,,
当且仅当,即时,等号成立.
所以,当时,在区间上取得最大值.
综上,当时,在区间上取得最大值,
即当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时.
21. 机床厂2001初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元.
(1)写出y与x之间的函数关系式;(2)从第几年开始,该机床开始盈利(盈利额为正值);
(3)使用若干年后,对机床的处理方案有两种:
(Ⅰ)当年平均盈利额达到最大值时,以30万元价格处理该机床;
(Ⅱ)当盈利额达到最大值时,以12万元价格处理该机床.
请你研究一下哪种方案处理较为合理?请说明理由
【答案】(1)依题得:
(2)解不等式
,故从第3年开始盈利.
(3)(Ⅰ)
当且仅当时,即时等号成立.
到2008年,年平均盈利额达到最大值,工厂共获利.
(Ⅱ),
故到2011年,盈利额达到最大值,工厂获利.
盈利额达到的最大值相同,而方案Ⅰ所用的时间较短,故方案Ⅰ比较合理.
22. 如图,函数的图象由两条射线及抛物线的一部分组成,求函数的解析式.
答案】 设左侧的射线对应解析式为y=kx+b(x≤1).∵点(1,1)、(0,2)在此射线上,
∴解得
∴左侧射线对应的函数的解析式为y=-x+2(x≤1).
同理,当x≥3时,函数的解析式为y=x-2
(x≥3).
再设抛物线对应的二次函数的解析式为
y=a(x-2)2+2(1≤x≤3,a<0),
则∵点(1,1)在抛物线上,
∴a+2=1,a=-1.
∴抛物线对应的二次函数的解析式为
y=-x2+4x-2(1≤x≤3).
综上所述,函数的解析式为
y=
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设集合A={x|1
C.(1,3) D.(1,2)∪(3,4)
【答案】B
2.已知集合则 ( )
A. B. C.{0, 2} D.{0,1, 2}
【答案】D
3.对于平面上的点集Ω,如果连接Ω中任意两点的线段必定包含于Ω,则称Ω为平面上的凸集,给出平面上4个点集的图形如图 (阴影区域及其边界),其中为凸集的是( )
A.①③ B.②③ C.③④ D.①④
【答案】B
4.函数f(x)=(a>0且a≠1)是R上的减函数,则a的取值范围是( )
A.(0,1) B.
C. D.
【答案】B
5. 设函数,若,则的取值范围是 ( )
A. B.
C. D.
【答案】B
6.函数y=()x+1的图像关于直线y=x对称的图像大致是( )
【答案】A
7.函数在区间()内的图象是 ( )
【答案】D
8.若点(a,b)在y=lgx图像上,a≠1,则下列点也在此图像上的是( )
A.(,b) B.(10a,1-b)
C.(,b+1) D.(a2,2b)
【答案】D
9.函数的值域为 ( )
A. B. C. D.
【答案】A
10.同时满足两个条件:①定义域内是减函数 ②定义域内是奇函数的函数是( )
A. B. C. D. =
【答案】A
11.设函数定义在实数集上,它的图象关于直线1对称,且当x1时,,则有 ( )
A. B.
C. D.
【答案】B
12.,则 ( )
A. B. C. D.
【答案】C
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.已知全集,集合和的关系的韦恩(Venn)图如图所示,则阴影部分所示的集合的元素共有 个.
【答案】2
14.函数关于直线x=1对称,则m=
【答案】
15.关于的不等式()的解集为 .
【答案】
16.定义在上的偶函数,对任意的均有成立,当时,,则直线与函数的图像交点中最近两点的距离等于 .
【答案】1
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.设集合A={(x,y)|y=2x-1,x∈N*},B={(x,y)|y=ax2-ax+a,x∈N*},问是否存在非零整数a,使A∩B≠ ?若存在,请求出a的值;若不存在,说明理由.
【答案】假设A∩B≠ ,则方程组
有正整数解,消去y得,
ax2-(a+2)x+a+1=0(*)
由Δ≥0,有(a+2)2-4a(a+1)≥0,
解得-≤a≤.
因a为非零整数,∴a=±1,
当a=-1时,代入(*),解得x=0或x=-1,
而x∈N*.故a≠-1.
当a=1时,代入(*),解得x=1或x=2,符合题意.
故存在a=1,使得A∩B≠ ,
此时A∩B={(1,1),(2,3)}.
18.已知奇函数f(x)在定义域[-2,2]上单调递减,求满足f(1-m)+f(1-m2)<0的实数m的取值范围.
【答案】由f(1-m)+f(1-m2)<0,
得f(1-m)<-f(1-m2).
又f(x)为奇函数,
∴f(1-m)
∴解得-1≤m<1.
∴实数m的取值范围为[-1,1).
19.已知函数与g(x)=m-x的图象有两个不同的交点,求实数m的取值范围.
【答案】与g(x)=m-x的图象如图.
由得x2-(2m-1)x+m2=0,
由Δ=(2m-1)2-4m2=0,
即f(x)与g(x)的图象恰有一个交点时,
依题意当0≤m时,
f(x)与g(x)的图象有两个不同的交点,
即实数m的取值范围是.
20.提高过江大桥的车辆通行能力可改善整个城市的交通状况,在一般情况下,大桥上的车流速度(单位:千米/小时)是车流密度(单位:辆/千米)的函数,当桥上的车流密度达到200辆/千米时,造成堵塞,此时车流速度为0;当车流密度不超过20辆/千米时,车流速度为60千米/小时,研究表明:当时,车流速度是车流密度的一次函数.
(Ⅰ)当时,求函数的表达式;
(Ⅱ)当车流密度为多大时,车流量(单位时间内通过桥上某观测点的车辆数,单位:辆/小时)可以达到最大,并求出最大值.(精确到1辆/小时)
【答案】(Ⅰ)由题意当时,;当时,设,
显然在是减函数,由已知得,
解得
故函数的表达式为=
(Ⅱ)依题意并由(Ⅰ)可得
当时,为增函数,故当时,其最大值为;
当时,,
当且仅当,即时,等号成立.
所以,当时,在区间上取得最大值.
综上,当时,在区间上取得最大值,
即当车流密度为100辆/千米时,车流量可以达到最大,最大值约为3333辆/小时.
21. 机床厂2001初用98万元购进一台数控机床,并立即投入生产使用,计划第一年维修、保养费用12万元,从第二年开始,每年所需维修、保养费用比上一年增加4万元,该机床使用后,每年的总收入为50万元,设使用x年后数控机床的盈利额为y万元.
(1)写出y与x之间的函数关系式;(2)从第几年开始,该机床开始盈利(盈利额为正值);
(3)使用若干年后,对机床的处理方案有两种:
(Ⅰ)当年平均盈利额达到最大值时,以30万元价格处理该机床;
(Ⅱ)当盈利额达到最大值时,以12万元价格处理该机床.
请你研究一下哪种方案处理较为合理?请说明理由
【答案】(1)依题得:
(2)解不等式
,故从第3年开始盈利.
(3)(Ⅰ)
当且仅当时,即时等号成立.
到2008年,年平均盈利额达到最大值,工厂共获利.
(Ⅱ),
故到2011年,盈利额达到最大值,工厂获利.
盈利额达到的最大值相同,而方案Ⅰ所用的时间较短,故方案Ⅰ比较合理.
22. 如图,函数的图象由两条射线及抛物线的一部分组成,求函数的解析式.
答案】 设左侧的射线对应解析式为y=kx+b(x≤1).∵点(1,1)、(0,2)在此射线上,
∴解得
∴左侧射线对应的函数的解析式为y=-x+2(x≤1).
同理,当x≥3时,函数的解析式为y=x-2
(x≥3).
再设抛物线对应的二次函数的解析式为
y=a(x-2)2+2(1≤x≤3,a<0),
则∵点(1,1)在抛物线上,
∴a+2=1,a=-1.
∴抛物线对应的二次函数的解析式为
y=-x2+4x-2(1≤x≤3).
综上所述,函数的解析式为
y=
同课章节目录
