贵州省三江口中学2013届高三上学期8月月考理科数学试题
文档属性
| 名称 | 贵州省三江口中学2013届高三上学期8月月考理科数学试题 | 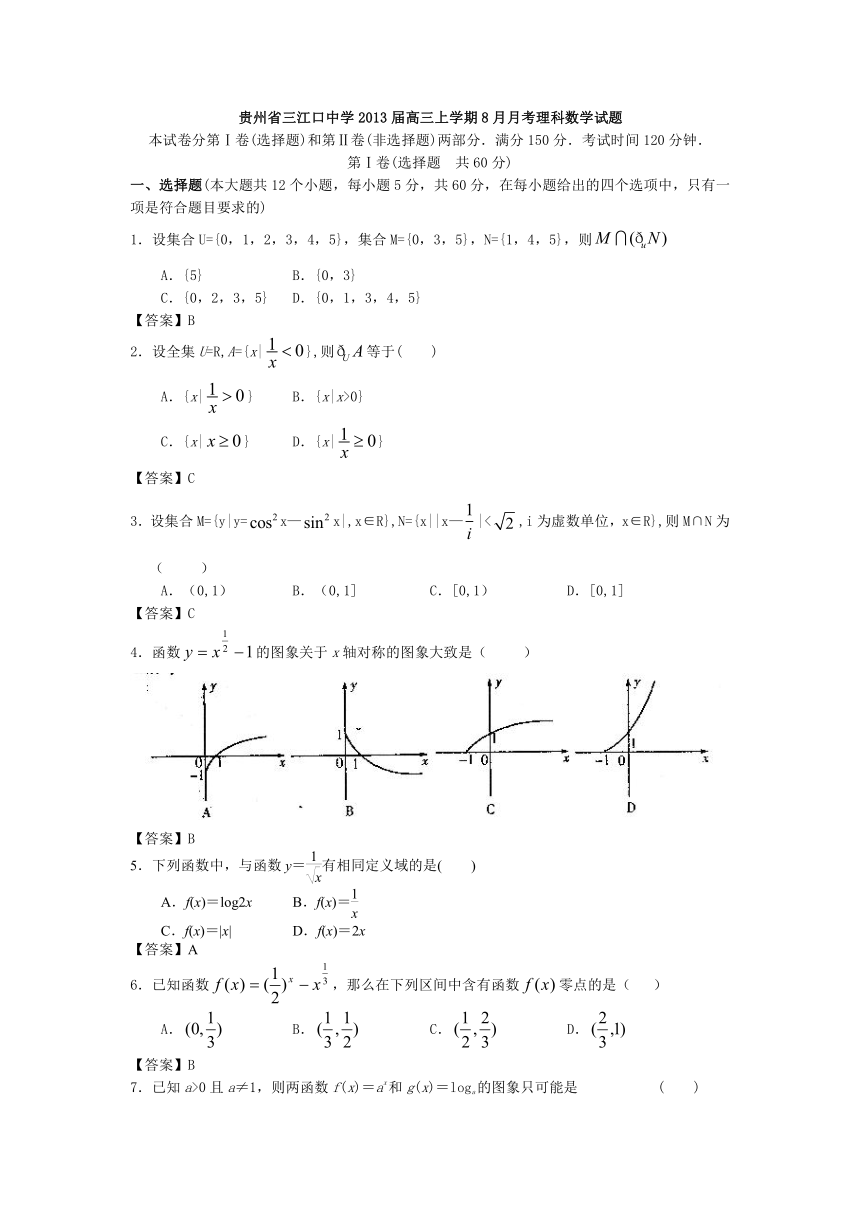 | |
| 格式 | zip | ||
| 文件大小 | 72.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-25 08:27:13 | ||
图片预览



文档简介
贵州省三江口中学2013届高三上学期8月月考理科数学试题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设集合U={0,1,2,3,4,5},集合M={0,3,5},N={1,4,5},则
A.{5} B.{0,3}
C.{0,2,3,5} D.{0,1,3,4,5}
【答案】B
2.设全集U=R,A={x|},则等于( )
A.{x|} B.{x|x>0}
C.{x|} D.{x|}
【答案】C
3.设集合M={y|y=x—x|,x∈R},N={x||x—|<,i为虚数单位,x∈R},则M∩N为( )
A.(0,1) B.(0,1] C.[0,1) D.[0,1]
【答案】C
4.函数的图象关于x轴对称的图象大致是( )
【答案】B
5.下列函数中,与函数y=有相同定义域的是( )
A.f(x)=log2x B.f(x)=
C.f(x)=|x| D.f(x)=2x
【答案】A
6.已知函数,那么在下列区间中含有函数零点的是( )
A. B. C. D.
【答案】B
7.已知a>0且a≠1,则两函数f(x)=ax和g(x)=loga的图象只可能是 ( )
【答案】C
8.函数在(0,2)内零点的个数为( )
A.0 B.1 C.2 D.4
【答案】B
9.设函数f(x)定义在实数集上,它的图象关于直线x=1对称,且当x≥1时,f(x)=2x-x,则有( )
A.fB.fC.fD.f【答案】B
10. 已知y=f(2x)的定义域为[-1,1],则y=f(log2x)的定义域为( )
A.[-1,1] B.[,2] C.[1,2] D.[,4]
【答案】D
11.根据统计,一名工人组装第x件某产品所用的时间(单位:分钟)为
f(x)=(A,c为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是( )
A.75,25 B.75,16
C.60,25 D.60,16
【答案】D
12.已知函数是偶函数,当时,有,且当时,的值域是,则的值是( )
A. B. C. D.
【答案】C
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.已知集合A={x|lx≥3},B={x|x≥a},若A B,则实数a的取值范围是(-∞,c],其中的c=______.
【答案】0
14.已知函数f(x)是定义域为R的奇函数,且f(-1)=2,那么f(0)+f(1)=________.
【答案】-2
15. 函数f(x)=loga(a>0且a≠1),f(2)=3,则f(-2)的值为__________.
【答案】-3
16.已知集合P={x|≤x≤3},函数f(x)=log2(ax2-2x+2)的定义域为Q.
(1)若P∩Q=[,),P∪Q=(-2,3],则实数a的值为__________;
(2)若P∩Q= ,则实数a的取值范围为__________.
【答案】(1)a=- (2)a≤-4
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.设A是实数集,满足若a∈A,则∈A,a≠1且 .
(1)若2∈A,则A中至少还有几个元素?求出这几个元素.
(2)A能否为单元素集合?请说明理由.
(3)若a∈A,证明:1-∈A.
【答案】(1)∵ 2∈A,
∴==-1∈A;
∴==∈A;
∴==2∈A.
因此,A中至少还有两个元素:-1和.
(2)如果A为单元素集合,则a=,整理得a2-a+1=0,该方程无实数解,故在实数范围内,A不可能是单元素集.
(3)证明: a∈A∈A ∈A∈A,即1-∈A.
18.某造纸厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图如图所示).如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/平方米,水池所有墙的厚度忽略不计.
试设计污水处理池的长和宽,使总造价最低,并求出最低总造价
【答案】设污水处理池的宽为x米,则长为米,
则总造价
当且仅当
当长为16.2米,宽为10米时吗,总造价最低,,最低总造价为38880元。
19.已知定义在实数集上的奇函数有最小正周期2,且当时,
(Ⅰ)求函数在上的解析式; (Ⅱ)判断在上的单调性;
(Ⅲ)当取何值时,方程在上有实数解?
【答案】(Ⅰ)∵f(x)是x∈R上的奇函数,∴f(0)=0.
设x∈(-1,0), 则-x∈(0,1),
(Ⅱ)设,
∵,∴,
∴
∴f(x)在(0,1)上为减函数.
(Ⅲ)∵f(x)在(0,1)上为减函数,
∴
方程上有实数解.
20.已知定义在R上的函数f(x)对任意实数x,y恒有f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,又f(1)=-.
(1)求证:f(x)为奇函数;
(2)求证:f(x)在R上是减函数;
(3)求f(x)在[-3,6]上的最大值与最小值.
【答案】(1)令x=y=0,可得f(0)+f(0)=f(0+0),从而f(0)=0.
令y=-x,可得f(x)+f(-x)=f(x-x)=f(0)=0.
即f(-x)=-f(x),故f(x)为奇函数.
(2)证明:设x1,x2∈R,且x1>x2,则x1-x2>0,于是f(x1-x2)<0,从而f(x1)-f(x2)
=f[(x1-x2)+x2]-f(x2)
=f(x1-x2)+f(x2)-f(x2)
=f(x1-x2)<0.
∴f(x)为减函数.
(3)由(2)知,所求函数的最大值为f(-3),最小值为f(6).
f(-3)=-f(3)=-[f(2)+f(1)]
=-2f(1)-f(1)=-3f(1)=2,
f(6)=-f(-6)=-[f(-3)+f(-3)]=-2f(-3)=-4.
于是f(x)在[-3,6]上的最大值为2,最小值为-4.
21.若函数与的图象关于原点对称,且,
(1)求的解析式;
(2)解不等式
【答案】(1)由题意得
由,得
或
或
∴,即不等式的解集为
22.定义在-1,1上的奇函数f(x)是减函数,且f(1-a)+f(1-a2)>0,求实数a的取值范围。
【答案】f(1-a)+f(1-a2)>0,得:f(1-a) >f(a2-1)
, 1
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.设集合U={0,1,2,3,4,5},集合M={0,3,5},N={1,4,5},则
A.{5} B.{0,3}
C.{0,2,3,5} D.{0,1,3,4,5}
【答案】B
2.设全集U=R,A={x|},则等于( )
A.{x|} B.{x|x>0}
C.{x|} D.{x|}
【答案】C
3.设集合M={y|y=x—x|,x∈R},N={x||x—|<,i为虚数单位,x∈R},则M∩N为( )
A.(0,1) B.(0,1] C.[0,1) D.[0,1]
【答案】C
4.函数的图象关于x轴对称的图象大致是( )
【答案】B
5.下列函数中,与函数y=有相同定义域的是( )
A.f(x)=log2x B.f(x)=
C.f(x)=|x| D.f(x)=2x
【答案】A
6.已知函数,那么在下列区间中含有函数零点的是( )
A. B. C. D.
【答案】B
7.已知a>0且a≠1,则两函数f(x)=ax和g(x)=loga的图象只可能是 ( )
【答案】C
8.函数在(0,2)内零点的个数为( )
A.0 B.1 C.2 D.4
【答案】B
9.设函数f(x)定义在实数集上,它的图象关于直线x=1对称,且当x≥1时,f(x)=2x-x,则有( )
A.f
10. 已知y=f(2x)的定义域为[-1,1],则y=f(log2x)的定义域为( )
A.[-1,1] B.[,2] C.[1,2] D.[,4]
【答案】D
11.根据统计,一名工人组装第x件某产品所用的时间(单位:分钟)为
f(x)=(A,c为常数).已知工人组装第4件产品用时30分钟,组装第A件产品用时15分钟,那么c和A的值分别是( )
A.75,25 B.75,16
C.60,25 D.60,16
【答案】D
12.已知函数是偶函数,当时,有,且当时,的值域是,则的值是( )
A. B. C. D.
【答案】C
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.已知集合A={x|lx≥3},B={x|x≥a},若A B,则实数a的取值范围是(-∞,c],其中的c=______.
【答案】0
14.已知函数f(x)是定义域为R的奇函数,且f(-1)=2,那么f(0)+f(1)=________.
【答案】-2
15. 函数f(x)=loga(a>0且a≠1),f(2)=3,则f(-2)的值为__________.
【答案】-3
16.已知集合P={x|≤x≤3},函数f(x)=log2(ax2-2x+2)的定义域为Q.
(1)若P∩Q=[,),P∪Q=(-2,3],则实数a的值为__________;
(2)若P∩Q= ,则实数a的取值范围为__________.
【答案】(1)a=- (2)a≤-4
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.设A是实数集,满足若a∈A,则∈A,a≠1且 .
(1)若2∈A,则A中至少还有几个元素?求出这几个元素.
(2)A能否为单元素集合?请说明理由.
(3)若a∈A,证明:1-∈A.
【答案】(1)∵ 2∈A,
∴==-1∈A;
∴==∈A;
∴==2∈A.
因此,A中至少还有两个元素:-1和.
(2)如果A为单元素集合,则a=,整理得a2-a+1=0,该方程无实数解,故在实数范围内,A不可能是单元素集.
(3)证明: a∈A∈A ∈A∈A,即1-∈A.
18.某造纸厂拟建一座平面图形为矩形且面积为162平方米的三级污水处理池,池的深度一定(平面图如图所示).如果池四周围墙建造单价为400元/米,中间两道隔墙建造单价为248元/米,池底建造单价为80元/平方米,水池所有墙的厚度忽略不计.
试设计污水处理池的长和宽,使总造价最低,并求出最低总造价
【答案】设污水处理池的宽为x米,则长为米,
则总造价
当且仅当
当长为16.2米,宽为10米时吗,总造价最低,,最低总造价为38880元。
19.已知定义在实数集上的奇函数有最小正周期2,且当时,
(Ⅰ)求函数在上的解析式; (Ⅱ)判断在上的单调性;
(Ⅲ)当取何值时,方程在上有实数解?
【答案】(Ⅰ)∵f(x)是x∈R上的奇函数,∴f(0)=0.
设x∈(-1,0), 则-x∈(0,1),
(Ⅱ)设,
∵,∴,
∴
∴f(x)在(0,1)上为减函数.
(Ⅲ)∵f(x)在(0,1)上为减函数,
∴
方程上有实数解.
20.已知定义在R上的函数f(x)对任意实数x,y恒有f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,又f(1)=-.
(1)求证:f(x)为奇函数;
(2)求证:f(x)在R上是减函数;
(3)求f(x)在[-3,6]上的最大值与最小值.
【答案】(1)令x=y=0,可得f(0)+f(0)=f(0+0),从而f(0)=0.
令y=-x,可得f(x)+f(-x)=f(x-x)=f(0)=0.
即f(-x)=-f(x),故f(x)为奇函数.
(2)证明:设x1,x2∈R,且x1>x2,则x1-x2>0,于是f(x1-x2)<0,从而f(x1)-f(x2)
=f[(x1-x2)+x2]-f(x2)
=f(x1-x2)+f(x2)-f(x2)
=f(x1-x2)<0.
∴f(x)为减函数.
(3)由(2)知,所求函数的最大值为f(-3),最小值为f(6).
f(-3)=-f(3)=-[f(2)+f(1)]
=-2f(1)-f(1)=-3f(1)=2,
f(6)=-f(-6)=-[f(-3)+f(-3)]=-2f(-3)=-4.
于是f(x)在[-3,6]上的最大值为2,最小值为-4.
21.若函数与的图象关于原点对称,且,
(1)求的解析式;
(2)解不等式
【答案】(1)由题意得
由,得
或
或
∴,即不等式的解集为
22.定义在-1,1上的奇函数f(x)是减函数,且f(1-a)+f(1-a2)>0,求实数a的取值范围。
【答案】f(1-a)+f(1-a2)>0,得:f(1-a) >f(a2-1)
, 1
同课章节目录
