2021-2022学年黑龙江省大庆市肇源县超等蒙古族乡学校等几校七年级(上)期中数学试卷(五四学制) (Word版含解析)
文档属性
| 名称 | 2021-2022学年黑龙江省大庆市肇源县超等蒙古族乡学校等几校七年级(上)期中数学试卷(五四学制) (Word版含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 517.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(五四学制) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 00:00:00 | ||
图片预览




文档简介
2021-2022学年黑龙江省大庆市肇源县超等蒙古族乡学校等几校七年级第一学期期中数学试卷(五四学制)
一、选择题:(每小题只有一个正确答案,每小题3分,共30分)
1.下列计算正确的是( )
A.a2 a3=a5
B.
C.
D.(x﹣y)2=x2﹣y2
2.下列各式中不能用平方差公式计算的是( )
A.(x+y)(﹣x+y) B.(﹣x+y)(﹣x﹣y)
C.(﹣x﹣y)(x﹣y) D.(x﹣y)(﹣x+y)
3.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂重物的质量x(kg)有下面的关系,那么弹簧总长y(cm)与所挂重物x(kg)之间的关系式为( )
x(kg) 0 1 2 3 4 5 6
y(cm) 12 12.5 13 13.5 14 14.5 15
A.y=0.5x+12 B.y=x+10.5 C.y=0.5x+10 D.y=x+12
4.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是( )
A.第一次右拐60°,第二次左拐120°
B.第一次左拐60°,第二次右拐60°
C.第一次左拐60°,第二次左拐120°
D.第一次右拐60°,第二次右拐60°
5.将一直角三角板与两边平行的纸条如图所示放置,下列结论:
(1)∠1=∠2;
(2)∠3=∠4;
(3)∠2+∠4=90°;
(4)∠4+∠5=180°,
其中正确的个数是( )
A.1 B.2 C.3 D.4
6.已知2m=3,2n=4,则23m﹣2n的值为( )
A. B. C. D.1
7.计算:2(a2)6﹣(a3)4的值为( )
A.﹣a12 B.a12 C.﹣a24 D.a24
8.如图,AB∥CD,∠AGE=128°,HM平分∠EHD,则∠MHD的度数是( )
A.46° B.23° C.26° D.24°
9.一个角的补角比这个角的余角大( )
A.70° B.80° C.90° D.100°
10.已知:a+b=m,ab=﹣4,化简(a﹣2)(b﹣2)的结果是( )
A.6 B.2m﹣8 C.2m D.﹣2m
二、耐心填一填(每题3分,共30分)
11.新冠病毒的直径约为0.000000003m,数据0.000000003m可用科学记数法表示为 .
12.如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置,若∠EFB=65°,则∠AED′等于 °.
13.若x2﹣mx+25是完全平方式,则m= .
14.汽车开始行驶时,油箱中有油40升,如果每小时耗油8升,则油箱内余油量y(升)与行驶时间x(小时)的关系式为 ,该汽车最多可行驶 小时.
15.多项式(mx+4)(2﹣3x)展开后不含x项,则m= .
16.a﹣=2,则a2= .
17.已知:如图,∠EAD=∠DCF,要得到AB∥CD,则需要的条件 .(填一个你认为正确的条件即可)
18.现规定一种运算:a※b=ab+a﹣b,其中a,b为实数,则a※b+(b﹣a)※b= .
19.如图,直线l1∥l2,AB⊥l1,垂足为O,BC与l2相交于点E,若∠1=43°,则∠2= 度.
20.∠AOB=45°,∠BOC=30°,则∠AOC= .
三、用心算一算:(本大题共8个小题,共60分。请认真在答题区域内作答。)
21.(16分)计算:
(1)m3 m2+m7÷m2+(m2)3;
(2)(π﹣3.14)0+(﹣0.125)2021×82021;
(3)(x+1)(x2﹣1)(x﹣1);
(4)2019×2021﹣20202(乘法公式计算);
(5)解方程:(2x+3)(x﹣4)﹣(x+2)(x﹣3)=x2+6.
22.已知a+b=8,ab=15,求下列式子的值:
(1)a2+b2;
(2)(a﹣b)2.
23.化简求值:已知x=3,y=2,求[(x+y)(x﹣y)﹣(x﹣2y)2﹣2y2]÷2y的值.
24.如图,∠1=∠2,DE⊥BC,AB⊥BC,那么∠A=∠3吗?说明理由.
解:∠A=∠3,理由如下:
∵DE⊥BC,AB⊥BC(已知)
∴∠DEB=∠ABC=90°( )
∴∠DEB+( )=180°
∴DE∥AB( )
∴∠1=∠A( )
∠2=∠3( )
∵∠1=∠2(已知)
∴∠A=∠3( )
25.如图,AB∥CD
(1)若∠A=30°,∠C=60°,则∠AEC= ;
(2)请猜想∠A、∠AEC、∠C之间有何数量关系?并说明理由.
26.已知:如图,∠1+∠2=180°,∠3=∠B,求证:∠AED=∠C.
27.若a2+b2﹣2a+4b+5=0,求a+b的值.
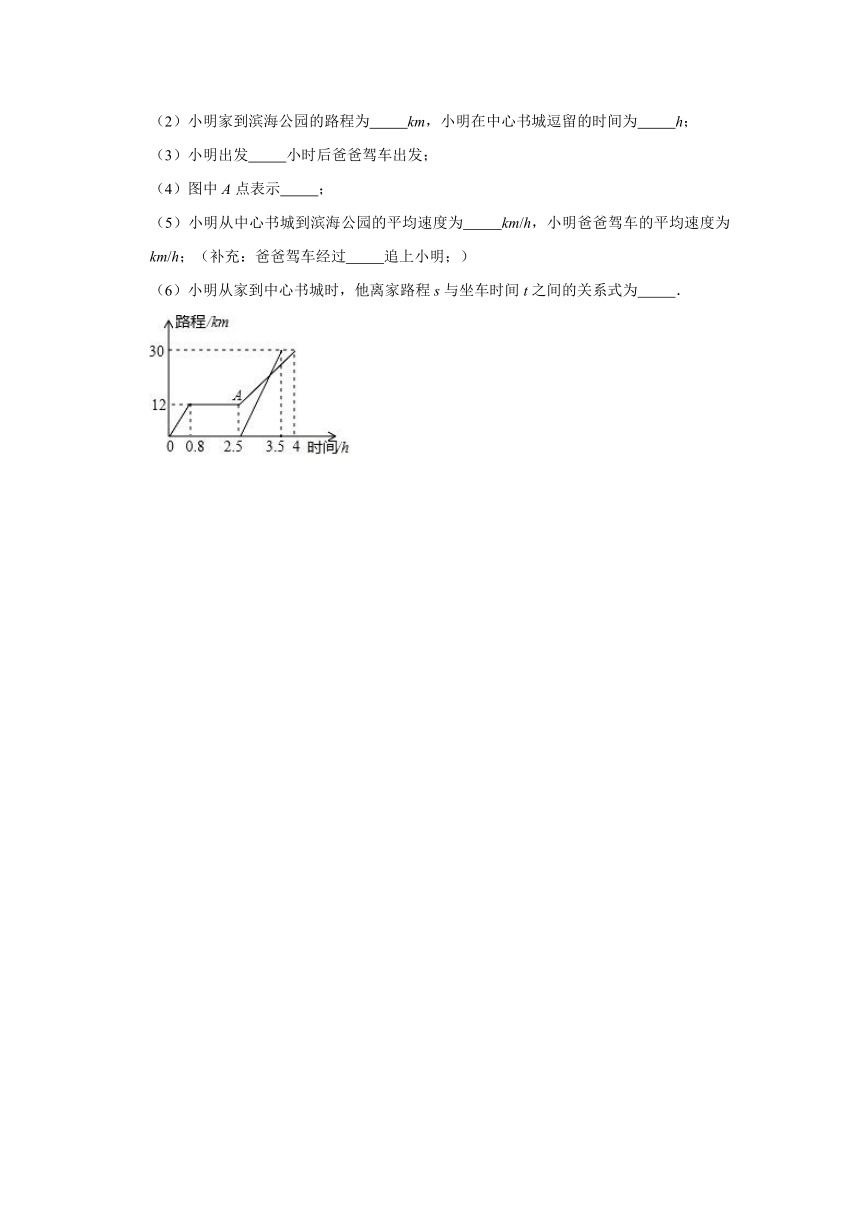
28.周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时后达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往滨海公园.如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)图中自变量是 ,因变量是 ;
(2)小明家到滨海公园的路程为 km,小明在中心书城逗留的时间为 h;
(3)小明出发 小时后爸爸驾车出发;
(4)图中A点表示 ;
(5)小明从中心书城到滨海公园的平均速度为 km/h,小明爸爸驾车的平均速度为 km/h;(补充:爸爸驾车经过 追上小明;)
(6)小明从家到中心书城时,他离家路程s与坐车时间t之间的关系式为 .
参考答案
一、选择题:(每小题只有一个正确答案,每小题3分,共30分)
1.下列计算正确的是( )
A.a2 a3=a5
B.
C.
D.(x﹣y)2=x2﹣y2
【分析】根据同底数幂的乘法、积的乘方与幂的乘方、负整数指数幂、完全平方公式解决此题.
解:A.根据同底数幂的乘法,a2 a3=a5,那么A正确,故A符合题意.
B.根据积的乘方与幂的乘方,,那么B不正确,故B不符合题意.
C.根据负整数指数幂,,那么C不正确,故C不符合题意.
D.根据完全平方公式,(x﹣y)2=x2﹣2xy+y2,那么D不正确,故D不符合题意.
故选:A.
2.下列各式中不能用平方差公式计算的是( )
A.(x+y)(﹣x+y) B.(﹣x+y)(﹣x﹣y)
C.(﹣x﹣y)(x﹣y) D.(x﹣y)(﹣x+y)
【分析】A:式子是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数;
B:式子是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数;
C:式子是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数;
D:式子是两个二项式相乘,并且这两个二项式中项完全相同,用完全平方公式计算.
解:A:原式=(x+y)(y﹣x)=y2﹣x2,∴不符合题意;
B:原式=(﹣x+y)(﹣x﹣y)=(﹣x)2﹣y2=x2﹣y2,∴不符合题意;
C:原式=(﹣y﹣x)(﹣y+x)=(﹣y)2﹣x2=y2﹣x2,∴不符合题意;
D:原式=﹣(x﹣y)(x﹣y)=﹣(x﹣y)2,∴符合题意;
故选:D.
3.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂重物的质量x(kg)有下面的关系,那么弹簧总长y(cm)与所挂重物x(kg)之间的关系式为( )
x(kg) 0 1 2 3 4 5 6
y(cm) 12 12.5 13 13.5 14 14.5 15
A.y=0.5x+12 B.y=x+10.5 C.y=0.5x+10 D.y=x+12
【分析】由上表可知12.5﹣12=0.5,13﹣12.5=0.5,13.5﹣13=0.5,14﹣13.5=0.5,14.5﹣14=0.5,15﹣14.5=0.5,0.5为常量,12也为常量.据此即可得出弹簧总长y(cm)与所挂重物x(kg)之间的函数关系式.
解:由表可知:常量为0.5;
所以,弹簧总长y(cm)与所挂重物x(kg)之间的函数关系式为y=0.5x+12.
故选:A.
4.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是( )
A.第一次右拐60°,第二次左拐120°
B.第一次左拐60°,第二次右拐60°
C.第一次左拐60°,第二次左拐120°
D.第一次右拐60°,第二次右拐60°
【分析】根据两条直线平行的性质:两条直线平行,同位角相等.再根据题意得:两次拐的方向不相同,但角度相等.
解:如图,第一次拐的角是∠1,第二次拐的角是∠2,由于平行前进,可以得到∠1=∠2.
故选:B.
5.将一直角三角板与两边平行的纸条如图所示放置,下列结论:
(1)∠1=∠2;
(2)∠3=∠4;
(3)∠2+∠4=90°;
(4)∠4+∠5=180°,
其中正确的个数是( )
A.1 B.2 C.3 D.4
【分析】根据两直线平行同位角相等,内错角相等,同旁内角互补,及直角三角板的特殊性解答.
解:∵纸条的两边平行,
∴(1)∠1=∠2(同位角);
(2)∠3=∠4(内错角);
(4)∠4+∠5=180°(同旁内角)均正确;
又∵直角三角板与纸条下线相交的角为90°,
∴(3)∠2+∠4=90°,正确.
故选:D.
6.已知2m=3,2n=4,则23m﹣2n的值为( )
A. B. C. D.1
【分析】逆向运用同底数幂的除法法则以及利用幂的乘方运算法则计算即可,同底数幂的除法法则:底数不变,指数相减;幂的乘方法则:底数不变,指数相乘.
解:∵2m=3,2n=4,
∴23m﹣2n=23m÷22n=(2m)3÷(2n)2=33÷42=.
故选:B.
7.计算:2(a2)6﹣(a3)4的值为( )
A.﹣a12 B.a12 C.﹣a24 D.a24
【分析】利用幂的乘方的法则以及合并同类项的法则对所求的式子进行运算即可.
解:2(a2)6﹣(a3)4
=2a12﹣a12
=a12.
故选:B.
8.如图,AB∥CD,∠AGE=128°,HM平分∠EHD,则∠MHD的度数是( )
A.46° B.23° C.26° D.24°
【分析】由题意可由平行线的性质,求出∠EHD的度数,再由HM平分∠EHD,即可求出∠MHD的度数.
解:由题意得:∠AGE=∠BGF=128°,
∵AB∥CD,
∴∠EHD=180°﹣∠BGF=52°,
又∵HM平分∠EHD,
∴∠MHD=∠EHD=26°.
故选:C.
9.一个角的补角比这个角的余角大( )
A.70° B.80° C.90° D.100°
【分析】根据余角与补角的定义解决此题.
解:设这个角为x,则这个角的余角为90°﹣x,补角为180°﹣x.
∵180°﹣x﹣(90°﹣x)=180°﹣x﹣90°+x=90°,
∴一个角的补角比这个角的余角大90°.
故选:C.
10.已知:a+b=m,ab=﹣4,化简(a﹣2)(b﹣2)的结果是( )
A.6 B.2m﹣8 C.2m D.﹣2m
【分析】(a﹣2)(b﹣2)=ab﹣2(a+b)+4,然后代入求值即可.
解:(a﹣2)(b﹣2)=ab﹣2(a+b)+4=﹣4﹣2m+4=﹣2m.
故选:D.
二、耐心填一填(每题3分,共30分)
11.新冠病毒的直径约为0.000000003m,数据0.000000003m可用科学记数法表示为 3×10﹣9m .
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数n由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.000000003m=3×10﹣9m,
故答案为:3×10﹣9m.
12.如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置,若∠EFB=65°,则∠AED′等于 50 °.
【分析】先根据平行线的性质得出∠DEF的度数,再根据翻折变换的性质得出∠D′EF的度数,根据平角的定义即可得出结论.
解:∵AD∥BC,∠EFB=65°,
∴∠DEF=65°,
又∵∠DEF=∠D′EF=65°,
∴∠D′EF=65°,
∴∠AED′=180°﹣65°﹣65°=50°.
故答案是:50.
13.若x2﹣mx+25是完全平方式,则m= ±10 .
【分析】原式利用完全平方公式的结构特征判断即可确定出m的值.
解:∵x2﹣mx+25是完全平方式,
∴m=±10,
故答案为:±10
14.汽车开始行驶时,油箱中有油40升,如果每小时耗油8升,则油箱内余油量y(升)与行驶时间x(小时)的关系式为 y=40﹣8x ,该汽车最多可行驶 5 小时.
【分析】根据:油箱内余油量=原有的油量﹣x小时消耗的油量,可列出函数关系式.
解:依题意得,油箱内余油量y(升)与行驶时间x(小时)的关系式为:y=40﹣8x,
当y=0时,40﹣8x=0,
解得:x=5,
即汽车最多可行驶5小时.
故答案为:y=40﹣8x;5.
15.多项式(mx+4)(2﹣3x)展开后不含x项,则m= 6 .
【分析】先将多项式展开,再合并同类项,然后根据题意即可解答.
解:∵(mx+4)(2﹣3x)
=2mx﹣3mx2+8﹣12x
=﹣3mx2+(2m﹣12)x+8
∵展开后不含x项
∴2m﹣12=0
即m=6
故填空答案:6.
16.a﹣=2,则a2= 6 .
【分析】将a﹣=2两边平方,即可求出答案.
解:(a﹣)2=a2﹣2+=4,
∴a2+=6,
故答案为:6
17.已知:如图,∠EAD=∠DCF,要得到AB∥CD,则需要的条件 ∠EAD=∠B .(填一个你认为正确的条件即可)
【分析】可以添加条件∠EAD=∠B,由已知,∠EAD=∠DCF,则∠B=∠DCF,由同位角相等,两直线平行,得出AB∥CD.
解:可以添加条件∠EAD=∠B,理由如下:
∵∠EAD=∠B,∠EAD=∠DCF,
∴∠B=∠DCF,
∴AB∥CD.
故答案为:∠EAD=∠B.
18.现规定一种运算:a※b=ab+a﹣b,其中a,b为实数,则a※b+(b﹣a)※b= b2﹣b .
【分析】根据规定的运算,进行转换式子,按照整式的运算法则计算即可.
解:a※b+(b﹣a)※b,
=ab+a﹣b+b(b﹣a)+b﹣a﹣b,
=b2﹣b.
19.如图,直线l1∥l2,AB⊥l1,垂足为O,BC与l2相交于点E,若∠1=43°,则∠2= 133 度.
【分析】两直线平行,同位角、内错角相等,据此即可解答.
解:过点B作BD∥l1,则BD∥l2,
∴∠ABD=∠AOF=90°,∠1=∠EBD=43°,
∴∠2=∠ABD+∠EBD=133°.
故答案为:133.
20.∠AOB=45°,∠BOC=30°,则∠AOC= 15°或75° .
【分析】利用角与角的位置关系计算.
解:此题要分情况:
当∠BOC在∠AOB的内部时,∠AOC=15°;
当∠BOC在∠AOB的外部时,∠AOC=75°.
故填15°或75°.
三、用心算一算:(本大题共8个小题,共60分。请认真在答题区域内作答。)
21.(16分)计算:
(1)m3 m2+m7÷m2+(m2)3;
(2)(π﹣3.14)0+(﹣0.125)2021×82021;
(3)(x+1)(x2﹣1)(x﹣1);
(4)2019×2021﹣20202(乘法公式计算);
(5)解方程:(2x+3)(x﹣4)﹣(x+2)(x﹣3)=x2+6.
【分析】(1)根据同底数幂的乘除法和幂的乘方可以解答本题;
(2)根据零指数幂和积的乘方可以解答本题;
(3)根据平方差公式和完全平方公式可以解答本题;
(4)根据平方差公式可以解答本题;
(5)根据解方程的方法:去括号、移项及合并同类项、系数化为1,可以求得该方程的解.
解:(1)m3 m2+m7÷m2+(m2)3
=m5+m5+m6
=2m5+m6;
(2)(π﹣3.14)0+(﹣0.125)2021×82021
=1+(﹣0.125×8)2021
=1+(﹣1)2021
=1+(﹣1)
=0;
(3)(x+1)(x2﹣1)(x﹣1)
=[(x+1)(x﹣1)](x2﹣1)
=(x2﹣1)(x2﹣1)
=x4﹣2x2+1;
(4)2019×2021﹣20202
=(2020﹣1)×(2020+1)﹣20202
=20202﹣1﹣20202
=﹣1;
(5)(2x+3)(x﹣4)﹣(x+2)(x﹣3)=x2+6,
去括号,得:2x2﹣5x﹣12﹣x2+x+6=x2+6,
移项及合并同类项,得:﹣4x=12,
系数化为1,得x=﹣3.
22.已知a+b=8,ab=15,求下列式子的值:
(1)a2+b2;
(2)(a﹣b)2.
【分析】(1)根据完全平方公式解决此题.
(2)根据完全平方公式解决此题.
解:(1)∵a+b=8,ab=15,
∴(a+b)2=a2+b2+2ab=a2+b2+30=64.
∴a2+b2=34.
(2)由(1)得:a2+b2=34.
∴(a﹣b)2=a2+b2﹣2ab=34﹣30=4.
23.化简求值:已知x=3,y=2,求[(x+y)(x﹣y)﹣(x﹣2y)2﹣2y2]÷2y的值.
【分析】根据整式的加减运算法则以及乘除运算法则进行化简,然后将x与y的值代入化简后的式子即可求出答案.
解:原式=[(x2﹣y2)﹣(x2﹣4xy+4y2)﹣2y2]÷2y
=(x2﹣y2﹣x2+4xy﹣4y2﹣2y2)÷2y
=(﹣7y2+4xy)÷2y,
=﹣3.5y+2x,
当x=3,y=2时,
原式=﹣7+6=﹣1.
24.如图,∠1=∠2,DE⊥BC,AB⊥BC,那么∠A=∠3吗?说明理由.
解:∠A=∠3,理由如下:
∵DE⊥BC,AB⊥BC(已知)
∴∠DEB=∠ABC=90°( 垂直的定义 )
∴∠DEB+( ∠ABC )=180°
∴DE∥AB( 同旁内角互补,两直线平行 )
∴∠1=∠A( 两直线平行,同位角相等 )
∠2=∠3( 两直线平行,内错角相等 )
∵∠1=∠2(已知)
∴∠A=∠3( 等量代换 )
【分析】先根据垂直定义得到∠DEC=∠ABC=90°,则利用平行线的判定可得DE∥AB,然后根据平行线得性质得到∠2=∠3,∠1=∠A,再利用等量代换可得∠A=∠3.
解:理由如下:
∵DE⊥BC,AB⊥BC(已知)
∴∠DEC=∠ABC=90°(垂直的定义),
∴∠DEB+(∠ABC)=180O
∴DE∥AB(同旁内角互补,两直线平行),
∴∠1=∠A (两直线平行,同位角相等),
由DE∥BC还可得到:
∠2=∠3 (两直线平行,内错角相等),
又∵∠1=∠2(已知)
∴∠A=∠3 (等量代换).
故答案为垂直的定义;∠ABC;同旁内角互补,两直线平行;两直线平行,同位角相等;两直线平行,内错角相等;等量代换.
25.如图,AB∥CD
(1)若∠A=30°,∠C=60°,则∠AEC= 90° ;
(2)请猜想∠A、∠AEC、∠C之间有何数量关系?并说明理由.
【分析】(1)过点E作EQ∥AB,即可得出EQ∥AB,AB∥CD.依据平行线的性质,即可得到∠AEC=∠AEQ+∠CEQ=∠A+∠C;
(2)方法同(1).
解:(1)如图,过点E作EQ∥AB.
∴∠AEQ=∠A(两直线平行,内错角相等)
∵EQ∥AB,AB∥CD.
∴EQ∥CD(平行于同一直线的两直线平行)
∴∠CEQ=∠C
∴∠AEC=∠AEQ+∠CEQ=∠A+∠C=90°,
故答案为:90°;
(2)如图,过点E作EQ∥AB.
∴∠AEQ=∠A(两直线平行,内错角相等)
∵EQ∥AB,AB∥CD.
∴EQ∥CD(平行于同一直线的两直线平行)
∴∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C,
即∠AEC=∠A+∠C.
26.已知:如图,∠1+∠2=180°,∠3=∠B,求证:∠AED=∠C.
【分析】要证明∠AED=∠C,则需证明DE∥BC.根据等角的补角相等,得∠DFE=∠2,根据内错角相等,得直线EF∥AB,则∠3=∠ADE,从而∠ADE=∠B,即可证明结论.
【解答】证明:∵∠1+∠2=180°,∠1+∠DFE=180°,
∴∠DFE=∠2,
∴EF∥AB,
∴∠3=∠ADE.
又∠3=∠B,
∴∠ADE=∠B,
∴DE∥BC,
∴∠AED=∠C.
27.若a2+b2﹣2a+4b+5=0,求a+b的值.
【分析】将a2+b2﹣2a+4b+5=0的左边分组配方,然后根据偶次方的非负性,可求出a,b的值,代入a+b即可.
解:∵a2+b2﹣2a+4b+5=0,
∴(a﹣1)2+(b+2)2=0,
∴a﹣1=0,b+2=0,
∴a=1,b=﹣2,
∴a+b=﹣1.
28.周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时后达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往滨海公园.如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)图中自变量是 t ,因变量是 ;
(2)小明家到滨海公园的路程为 30 km,小明在中心书城逗留的时间为 1.7 h;
(3)小明出发 2.5 小时后爸爸驾车出发;
(4)图中A点表示 2.5小时后小明继续坐公交车到滨海公园 ;
(5)小明从中心书城到滨海公园的平均速度为 12 km/h,小明爸爸驾车的平均速度为 30 km/h;(补充:爸爸驾车经过 h 追上小明;)
(6)小明从家到中心书城时,他离家路程s与坐车时间t之间的关系式为 s=15t(0≤t≤0.8) .
【分析】(1)根据图象进行判断,即可得出自变量与因变量;
(2)根据图象中数据进行计算,即可得到路程与时间;
(3)根据梯形即可得到爸爸驾车出发的时间;
(4)根据点A的坐标即可得到点A的实际意义;
(5)根据相应的路程除以时间,即可得出速度;
(6)根据小明从家到中心书城时的速度,即可得到离家路程s与坐车时间t之间的关系式.
解:(1)由图可得,自变量是t,因变量是s,
故答案为:t,s;
(2)由图可得,小明家到滨海公园的路程为30km,小明在中心书城逗留的时间为2.5﹣0.8=1.7(h);
故答案为:30,1.7;
(3)由图可得,小明出发2.5小时后爸爸驾车出发;
故答案为:2.5;
(4)由图可得,A点表示2.5小时后小明继续坐公交车到滨海公园;
故答案为:2.5小时后小明继续坐公交车到滨海公园;
(5)小明从中心书城到滨海公园的平均速度为=12km/h,
小明爸爸驾车的平均速度为=30km/h;
爸爸驾车经过=h追上小明;
故答案为:12,30,h;
(6)小明从家到中心书城时,他的速度为=15km/h,
∴他离家路程s与坐车时间t之间的关系式为s=15t(0≤t≤0.8),
故答案为:s=15t(0≤t≤0.8).
一、选择题:(每小题只有一个正确答案,每小题3分,共30分)
1.下列计算正确的是( )
A.a2 a3=a5
B.
C.
D.(x﹣y)2=x2﹣y2
2.下列各式中不能用平方差公式计算的是( )
A.(x+y)(﹣x+y) B.(﹣x+y)(﹣x﹣y)
C.(﹣x﹣y)(x﹣y) D.(x﹣y)(﹣x+y)
3.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂重物的质量x(kg)有下面的关系,那么弹簧总长y(cm)与所挂重物x(kg)之间的关系式为( )
x(kg) 0 1 2 3 4 5 6
y(cm) 12 12.5 13 13.5 14 14.5 15
A.y=0.5x+12 B.y=x+10.5 C.y=0.5x+10 D.y=x+12
4.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是( )
A.第一次右拐60°,第二次左拐120°
B.第一次左拐60°,第二次右拐60°
C.第一次左拐60°,第二次左拐120°
D.第一次右拐60°,第二次右拐60°
5.将一直角三角板与两边平行的纸条如图所示放置,下列结论:
(1)∠1=∠2;
(2)∠3=∠4;
(3)∠2+∠4=90°;
(4)∠4+∠5=180°,
其中正确的个数是( )
A.1 B.2 C.3 D.4
6.已知2m=3,2n=4,则23m﹣2n的值为( )
A. B. C. D.1
7.计算:2(a2)6﹣(a3)4的值为( )
A.﹣a12 B.a12 C.﹣a24 D.a24
8.如图,AB∥CD,∠AGE=128°,HM平分∠EHD,则∠MHD的度数是( )
A.46° B.23° C.26° D.24°
9.一个角的补角比这个角的余角大( )
A.70° B.80° C.90° D.100°
10.已知:a+b=m,ab=﹣4,化简(a﹣2)(b﹣2)的结果是( )
A.6 B.2m﹣8 C.2m D.﹣2m
二、耐心填一填(每题3分,共30分)
11.新冠病毒的直径约为0.000000003m,数据0.000000003m可用科学记数法表示为 .
12.如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置,若∠EFB=65°,则∠AED′等于 °.
13.若x2﹣mx+25是完全平方式,则m= .
14.汽车开始行驶时,油箱中有油40升,如果每小时耗油8升,则油箱内余油量y(升)与行驶时间x(小时)的关系式为 ,该汽车最多可行驶 小时.
15.多项式(mx+4)(2﹣3x)展开后不含x项,则m= .
16.a﹣=2,则a2= .
17.已知:如图,∠EAD=∠DCF,要得到AB∥CD,则需要的条件 .(填一个你认为正确的条件即可)
18.现规定一种运算:a※b=ab+a﹣b,其中a,b为实数,则a※b+(b﹣a)※b= .
19.如图,直线l1∥l2,AB⊥l1,垂足为O,BC与l2相交于点E,若∠1=43°,则∠2= 度.
20.∠AOB=45°,∠BOC=30°,则∠AOC= .
三、用心算一算:(本大题共8个小题,共60分。请认真在答题区域内作答。)
21.(16分)计算:
(1)m3 m2+m7÷m2+(m2)3;
(2)(π﹣3.14)0+(﹣0.125)2021×82021;
(3)(x+1)(x2﹣1)(x﹣1);
(4)2019×2021﹣20202(乘法公式计算);
(5)解方程:(2x+3)(x﹣4)﹣(x+2)(x﹣3)=x2+6.
22.已知a+b=8,ab=15,求下列式子的值:
(1)a2+b2;
(2)(a﹣b)2.
23.化简求值:已知x=3,y=2,求[(x+y)(x﹣y)﹣(x﹣2y)2﹣2y2]÷2y的值.
24.如图,∠1=∠2,DE⊥BC,AB⊥BC,那么∠A=∠3吗?说明理由.
解:∠A=∠3,理由如下:
∵DE⊥BC,AB⊥BC(已知)
∴∠DEB=∠ABC=90°( )
∴∠DEB+( )=180°
∴DE∥AB( )
∴∠1=∠A( )
∠2=∠3( )
∵∠1=∠2(已知)
∴∠A=∠3( )
25.如图,AB∥CD
(1)若∠A=30°,∠C=60°,则∠AEC= ;
(2)请猜想∠A、∠AEC、∠C之间有何数量关系?并说明理由.
26.已知:如图,∠1+∠2=180°,∠3=∠B,求证:∠AED=∠C.
27.若a2+b2﹣2a+4b+5=0,求a+b的值.
28.周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时后达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往滨海公园.如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)图中自变量是 ,因变量是 ;
(2)小明家到滨海公园的路程为 km,小明在中心书城逗留的时间为 h;
(3)小明出发 小时后爸爸驾车出发;
(4)图中A点表示 ;
(5)小明从中心书城到滨海公园的平均速度为 km/h,小明爸爸驾车的平均速度为 km/h;(补充:爸爸驾车经过 追上小明;)
(6)小明从家到中心书城时,他离家路程s与坐车时间t之间的关系式为 .
参考答案
一、选择题:(每小题只有一个正确答案,每小题3分,共30分)
1.下列计算正确的是( )
A.a2 a3=a5
B.
C.
D.(x﹣y)2=x2﹣y2
【分析】根据同底数幂的乘法、积的乘方与幂的乘方、负整数指数幂、完全平方公式解决此题.
解:A.根据同底数幂的乘法,a2 a3=a5,那么A正确,故A符合题意.
B.根据积的乘方与幂的乘方,,那么B不正确,故B不符合题意.
C.根据负整数指数幂,,那么C不正确,故C不符合题意.
D.根据完全平方公式,(x﹣y)2=x2﹣2xy+y2,那么D不正确,故D不符合题意.
故选:A.
2.下列各式中不能用平方差公式计算的是( )
A.(x+y)(﹣x+y) B.(﹣x+y)(﹣x﹣y)
C.(﹣x﹣y)(x﹣y) D.(x﹣y)(﹣x+y)
【分析】A:式子是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数;
B:式子是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数;
C:式子是两个二项式相乘,并且这两个二项式中有一项完全相同,另一项互为相反数;
D:式子是两个二项式相乘,并且这两个二项式中项完全相同,用完全平方公式计算.
解:A:原式=(x+y)(y﹣x)=y2﹣x2,∴不符合题意;
B:原式=(﹣x+y)(﹣x﹣y)=(﹣x)2﹣y2=x2﹣y2,∴不符合题意;
C:原式=(﹣y﹣x)(﹣y+x)=(﹣y)2﹣x2=y2﹣x2,∴不符合题意;
D:原式=﹣(x﹣y)(x﹣y)=﹣(x﹣y)2,∴符合题意;
故选:D.
3.弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂重物的质量x(kg)有下面的关系,那么弹簧总长y(cm)与所挂重物x(kg)之间的关系式为( )
x(kg) 0 1 2 3 4 5 6
y(cm) 12 12.5 13 13.5 14 14.5 15
A.y=0.5x+12 B.y=x+10.5 C.y=0.5x+10 D.y=x+12
【分析】由上表可知12.5﹣12=0.5,13﹣12.5=0.5,13.5﹣13=0.5,14﹣13.5=0.5,14.5﹣14=0.5,15﹣14.5=0.5,0.5为常量,12也为常量.据此即可得出弹簧总长y(cm)与所挂重物x(kg)之间的函数关系式.
解:由表可知:常量为0.5;
所以,弹簧总长y(cm)与所挂重物x(kg)之间的函数关系式为y=0.5x+12.
故选:A.
4.一辆汽车在笔直的公路上行驶,两次拐弯后,仍在原来的方向上平行前进,那么两次拐弯的角度是( )
A.第一次右拐60°,第二次左拐120°
B.第一次左拐60°,第二次右拐60°
C.第一次左拐60°,第二次左拐120°
D.第一次右拐60°,第二次右拐60°
【分析】根据两条直线平行的性质:两条直线平行,同位角相等.再根据题意得:两次拐的方向不相同,但角度相等.
解:如图,第一次拐的角是∠1,第二次拐的角是∠2,由于平行前进,可以得到∠1=∠2.
故选:B.
5.将一直角三角板与两边平行的纸条如图所示放置,下列结论:
(1)∠1=∠2;
(2)∠3=∠4;
(3)∠2+∠4=90°;
(4)∠4+∠5=180°,
其中正确的个数是( )
A.1 B.2 C.3 D.4
【分析】根据两直线平行同位角相等,内错角相等,同旁内角互补,及直角三角板的特殊性解答.
解:∵纸条的两边平行,
∴(1)∠1=∠2(同位角);
(2)∠3=∠4(内错角);
(4)∠4+∠5=180°(同旁内角)均正确;
又∵直角三角板与纸条下线相交的角为90°,
∴(3)∠2+∠4=90°,正确.
故选:D.
6.已知2m=3,2n=4,则23m﹣2n的值为( )
A. B. C. D.1
【分析】逆向运用同底数幂的除法法则以及利用幂的乘方运算法则计算即可,同底数幂的除法法则:底数不变,指数相减;幂的乘方法则:底数不变,指数相乘.
解:∵2m=3,2n=4,
∴23m﹣2n=23m÷22n=(2m)3÷(2n)2=33÷42=.
故选:B.
7.计算:2(a2)6﹣(a3)4的值为( )
A.﹣a12 B.a12 C.﹣a24 D.a24
【分析】利用幂的乘方的法则以及合并同类项的法则对所求的式子进行运算即可.
解:2(a2)6﹣(a3)4
=2a12﹣a12
=a12.
故选:B.
8.如图,AB∥CD,∠AGE=128°,HM平分∠EHD,则∠MHD的度数是( )
A.46° B.23° C.26° D.24°
【分析】由题意可由平行线的性质,求出∠EHD的度数,再由HM平分∠EHD,即可求出∠MHD的度数.
解:由题意得:∠AGE=∠BGF=128°,
∵AB∥CD,
∴∠EHD=180°﹣∠BGF=52°,
又∵HM平分∠EHD,
∴∠MHD=∠EHD=26°.
故选:C.
9.一个角的补角比这个角的余角大( )
A.70° B.80° C.90° D.100°
【分析】根据余角与补角的定义解决此题.
解:设这个角为x,则这个角的余角为90°﹣x,补角为180°﹣x.
∵180°﹣x﹣(90°﹣x)=180°﹣x﹣90°+x=90°,
∴一个角的补角比这个角的余角大90°.
故选:C.
10.已知:a+b=m,ab=﹣4,化简(a﹣2)(b﹣2)的结果是( )
A.6 B.2m﹣8 C.2m D.﹣2m
【分析】(a﹣2)(b﹣2)=ab﹣2(a+b)+4,然后代入求值即可.
解:(a﹣2)(b﹣2)=ab﹣2(a+b)+4=﹣4﹣2m+4=﹣2m.
故选:D.
二、耐心填一填(每题3分,共30分)
11.新冠病毒的直径约为0.000000003m,数据0.000000003m可用科学记数法表示为 3×10﹣9m .
【分析】绝对值小于1的正数也可以利用科学记数法表示,一般形式为a×10﹣n,与较大数的科学记数法不同的是其所使用的是负整数指数幂,指数n由原数左边起第一个不为零的数字前面的0的个数所决定.
解:0.000000003m=3×10﹣9m,
故答案为:3×10﹣9m.
12.如图,把一个长方形纸片沿EF折叠后,点D,C分别落在D′,C′的位置,若∠EFB=65°,则∠AED′等于 50 °.
【分析】先根据平行线的性质得出∠DEF的度数,再根据翻折变换的性质得出∠D′EF的度数,根据平角的定义即可得出结论.
解:∵AD∥BC,∠EFB=65°,
∴∠DEF=65°,
又∵∠DEF=∠D′EF=65°,
∴∠D′EF=65°,
∴∠AED′=180°﹣65°﹣65°=50°.
故答案是:50.
13.若x2﹣mx+25是完全平方式,则m= ±10 .
【分析】原式利用完全平方公式的结构特征判断即可确定出m的值.
解:∵x2﹣mx+25是完全平方式,
∴m=±10,
故答案为:±10
14.汽车开始行驶时,油箱中有油40升,如果每小时耗油8升,则油箱内余油量y(升)与行驶时间x(小时)的关系式为 y=40﹣8x ,该汽车最多可行驶 5 小时.
【分析】根据:油箱内余油量=原有的油量﹣x小时消耗的油量,可列出函数关系式.
解:依题意得,油箱内余油量y(升)与行驶时间x(小时)的关系式为:y=40﹣8x,
当y=0时,40﹣8x=0,
解得:x=5,
即汽车最多可行驶5小时.
故答案为:y=40﹣8x;5.
15.多项式(mx+4)(2﹣3x)展开后不含x项,则m= 6 .
【分析】先将多项式展开,再合并同类项,然后根据题意即可解答.
解:∵(mx+4)(2﹣3x)
=2mx﹣3mx2+8﹣12x
=﹣3mx2+(2m﹣12)x+8
∵展开后不含x项
∴2m﹣12=0
即m=6
故填空答案:6.
16.a﹣=2,则a2= 6 .
【分析】将a﹣=2两边平方,即可求出答案.
解:(a﹣)2=a2﹣2+=4,
∴a2+=6,
故答案为:6
17.已知:如图,∠EAD=∠DCF,要得到AB∥CD,则需要的条件 ∠EAD=∠B .(填一个你认为正确的条件即可)
【分析】可以添加条件∠EAD=∠B,由已知,∠EAD=∠DCF,则∠B=∠DCF,由同位角相等,两直线平行,得出AB∥CD.
解:可以添加条件∠EAD=∠B,理由如下:
∵∠EAD=∠B,∠EAD=∠DCF,
∴∠B=∠DCF,
∴AB∥CD.
故答案为:∠EAD=∠B.
18.现规定一种运算:a※b=ab+a﹣b,其中a,b为实数,则a※b+(b﹣a)※b= b2﹣b .
【分析】根据规定的运算,进行转换式子,按照整式的运算法则计算即可.
解:a※b+(b﹣a)※b,
=ab+a﹣b+b(b﹣a)+b﹣a﹣b,
=b2﹣b.
19.如图,直线l1∥l2,AB⊥l1,垂足为O,BC与l2相交于点E,若∠1=43°,则∠2= 133 度.
【分析】两直线平行,同位角、内错角相等,据此即可解答.
解:过点B作BD∥l1,则BD∥l2,
∴∠ABD=∠AOF=90°,∠1=∠EBD=43°,
∴∠2=∠ABD+∠EBD=133°.
故答案为:133.
20.∠AOB=45°,∠BOC=30°,则∠AOC= 15°或75° .
【分析】利用角与角的位置关系计算.
解:此题要分情况:
当∠BOC在∠AOB的内部时,∠AOC=15°;
当∠BOC在∠AOB的外部时,∠AOC=75°.
故填15°或75°.
三、用心算一算:(本大题共8个小题,共60分。请认真在答题区域内作答。)
21.(16分)计算:
(1)m3 m2+m7÷m2+(m2)3;
(2)(π﹣3.14)0+(﹣0.125)2021×82021;
(3)(x+1)(x2﹣1)(x﹣1);
(4)2019×2021﹣20202(乘法公式计算);
(5)解方程:(2x+3)(x﹣4)﹣(x+2)(x﹣3)=x2+6.
【分析】(1)根据同底数幂的乘除法和幂的乘方可以解答本题;
(2)根据零指数幂和积的乘方可以解答本题;
(3)根据平方差公式和完全平方公式可以解答本题;
(4)根据平方差公式可以解答本题;
(5)根据解方程的方法:去括号、移项及合并同类项、系数化为1,可以求得该方程的解.
解:(1)m3 m2+m7÷m2+(m2)3
=m5+m5+m6
=2m5+m6;
(2)(π﹣3.14)0+(﹣0.125)2021×82021
=1+(﹣0.125×8)2021
=1+(﹣1)2021
=1+(﹣1)
=0;
(3)(x+1)(x2﹣1)(x﹣1)
=[(x+1)(x﹣1)](x2﹣1)
=(x2﹣1)(x2﹣1)
=x4﹣2x2+1;
(4)2019×2021﹣20202
=(2020﹣1)×(2020+1)﹣20202
=20202﹣1﹣20202
=﹣1;
(5)(2x+3)(x﹣4)﹣(x+2)(x﹣3)=x2+6,
去括号,得:2x2﹣5x﹣12﹣x2+x+6=x2+6,
移项及合并同类项,得:﹣4x=12,
系数化为1,得x=﹣3.
22.已知a+b=8,ab=15,求下列式子的值:
(1)a2+b2;
(2)(a﹣b)2.
【分析】(1)根据完全平方公式解决此题.
(2)根据完全平方公式解决此题.
解:(1)∵a+b=8,ab=15,
∴(a+b)2=a2+b2+2ab=a2+b2+30=64.
∴a2+b2=34.
(2)由(1)得:a2+b2=34.
∴(a﹣b)2=a2+b2﹣2ab=34﹣30=4.
23.化简求值:已知x=3,y=2,求[(x+y)(x﹣y)﹣(x﹣2y)2﹣2y2]÷2y的值.
【分析】根据整式的加减运算法则以及乘除运算法则进行化简,然后将x与y的值代入化简后的式子即可求出答案.
解:原式=[(x2﹣y2)﹣(x2﹣4xy+4y2)﹣2y2]÷2y
=(x2﹣y2﹣x2+4xy﹣4y2﹣2y2)÷2y
=(﹣7y2+4xy)÷2y,
=﹣3.5y+2x,
当x=3,y=2时,
原式=﹣7+6=﹣1.
24.如图,∠1=∠2,DE⊥BC,AB⊥BC,那么∠A=∠3吗?说明理由.
解:∠A=∠3,理由如下:
∵DE⊥BC,AB⊥BC(已知)
∴∠DEB=∠ABC=90°( 垂直的定义 )
∴∠DEB+( ∠ABC )=180°
∴DE∥AB( 同旁内角互补,两直线平行 )
∴∠1=∠A( 两直线平行,同位角相等 )
∠2=∠3( 两直线平行,内错角相等 )
∵∠1=∠2(已知)
∴∠A=∠3( 等量代换 )
【分析】先根据垂直定义得到∠DEC=∠ABC=90°,则利用平行线的判定可得DE∥AB,然后根据平行线得性质得到∠2=∠3,∠1=∠A,再利用等量代换可得∠A=∠3.
解:理由如下:
∵DE⊥BC,AB⊥BC(已知)
∴∠DEC=∠ABC=90°(垂直的定义),
∴∠DEB+(∠ABC)=180O
∴DE∥AB(同旁内角互补,两直线平行),
∴∠1=∠A (两直线平行,同位角相等),
由DE∥BC还可得到:
∠2=∠3 (两直线平行,内错角相等),
又∵∠1=∠2(已知)
∴∠A=∠3 (等量代换).
故答案为垂直的定义;∠ABC;同旁内角互补,两直线平行;两直线平行,同位角相等;两直线平行,内错角相等;等量代换.
25.如图,AB∥CD
(1)若∠A=30°,∠C=60°,则∠AEC= 90° ;
(2)请猜想∠A、∠AEC、∠C之间有何数量关系?并说明理由.
【分析】(1)过点E作EQ∥AB,即可得出EQ∥AB,AB∥CD.依据平行线的性质,即可得到∠AEC=∠AEQ+∠CEQ=∠A+∠C;
(2)方法同(1).
解:(1)如图,过点E作EQ∥AB.
∴∠AEQ=∠A(两直线平行,内错角相等)
∵EQ∥AB,AB∥CD.
∴EQ∥CD(平行于同一直线的两直线平行)
∴∠CEQ=∠C
∴∠AEC=∠AEQ+∠CEQ=∠A+∠C=90°,
故答案为:90°;
(2)如图,过点E作EQ∥AB.
∴∠AEQ=∠A(两直线平行,内错角相等)
∵EQ∥AB,AB∥CD.
∴EQ∥CD(平行于同一直线的两直线平行)
∴∠CEQ=∠C
∴∠AEQ+∠CEQ=∠A+∠C,
即∠AEC=∠A+∠C.
26.已知:如图,∠1+∠2=180°,∠3=∠B,求证:∠AED=∠C.
【分析】要证明∠AED=∠C,则需证明DE∥BC.根据等角的补角相等,得∠DFE=∠2,根据内错角相等,得直线EF∥AB,则∠3=∠ADE,从而∠ADE=∠B,即可证明结论.
【解答】证明:∵∠1+∠2=180°,∠1+∠DFE=180°,
∴∠DFE=∠2,
∴EF∥AB,
∴∠3=∠ADE.
又∠3=∠B,
∴∠ADE=∠B,
∴DE∥BC,
∴∠AED=∠C.
27.若a2+b2﹣2a+4b+5=0,求a+b的值.
【分析】将a2+b2﹣2a+4b+5=0的左边分组配方,然后根据偶次方的非负性,可求出a,b的值,代入a+b即可.
解:∵a2+b2﹣2a+4b+5=0,
∴(a﹣1)2+(b+2)2=0,
∴a﹣1=0,b+2=0,
∴a=1,b=﹣2,
∴a+b=﹣1.
28.周末,小明坐公交车到滨海公园游玩,他从家出发0.8小时后达到中心书城,逗留一段时间后继续坐公交车到滨海公园,小明离家一段时间后,爸爸驾车沿相同的路线前往滨海公园.如图是他们离家路程s(km)与小明离家时间t(h)的关系图,请根据图回答下列问题:
(1)图中自变量是 t ,因变量是 ;
(2)小明家到滨海公园的路程为 30 km,小明在中心书城逗留的时间为 1.7 h;
(3)小明出发 2.5 小时后爸爸驾车出发;
(4)图中A点表示 2.5小时后小明继续坐公交车到滨海公园 ;
(5)小明从中心书城到滨海公园的平均速度为 12 km/h,小明爸爸驾车的平均速度为 30 km/h;(补充:爸爸驾车经过 h 追上小明;)
(6)小明从家到中心书城时,他离家路程s与坐车时间t之间的关系式为 s=15t(0≤t≤0.8) .
【分析】(1)根据图象进行判断,即可得出自变量与因变量;
(2)根据图象中数据进行计算,即可得到路程与时间;
(3)根据梯形即可得到爸爸驾车出发的时间;
(4)根据点A的坐标即可得到点A的实际意义;
(5)根据相应的路程除以时间,即可得出速度;
(6)根据小明从家到中心书城时的速度,即可得到离家路程s与坐车时间t之间的关系式.
解:(1)由图可得,自变量是t,因变量是s,
故答案为:t,s;
(2)由图可得,小明家到滨海公园的路程为30km,小明在中心书城逗留的时间为2.5﹣0.8=1.7(h);
故答案为:30,1.7;
(3)由图可得,小明出发2.5小时后爸爸驾车出发;
故答案为:2.5;
(4)由图可得,A点表示2.5小时后小明继续坐公交车到滨海公园;
故答案为:2.5小时后小明继续坐公交车到滨海公园;
(5)小明从中心书城到滨海公园的平均速度为=12km/h,
小明爸爸驾车的平均速度为=30km/h;
爸爸驾车经过=h追上小明;
故答案为:12,30,h;
(6)小明从家到中心书城时,他的速度为=15km/h,
∴他离家路程s与坐车时间t之间的关系式为s=15t(0≤t≤0.8),
故答案为:s=15t(0≤t≤0.8).
同课章节目录
