2021-2022学年安徽省合肥五十中东校九年级(上)期中数学试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年安徽省合肥五十中东校九年级(上)期中数学试卷(Word版 含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 880.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 07:18:15 | ||
图片预览



文档简介
2021-2022学年安徽省合肥五十中东校九年级第一学期期中数学试卷
一、选择题(本大题共10小题,每小题4分,满分40分)
1.将抛物线y=﹣2x2﹣3向左平移4个单位,再向上平移1个单位所得新抛物线的表达式为( )
A.y=﹣2(x﹣4)2﹣4 B.y=﹣2(x+4)2﹣2
C.y=﹣2x2+4 D.y=﹣2x2+4
2.把二次函数y=x2+4x﹣3化成y=a(x+h)2+k的形式,正确的是( )
A.y=(x+2)2﹣7 B.y=(x﹣2)2+7 C.y=(x﹣2)2﹣7 D.y=(x+2)2+1
3.对于二次函数y=﹣(x+2)2+3的图象,下列说法正确的是( )
A.开口向上 B.当x=2时,y有最小值是3
C.对称轴是x=2 D.顶点坐标是(﹣2,3)
4.下列四组线段中,成比例线段的有( )
A.1m、2m、3m、6dm B.2m、4m、9m、18cm
C.1m、m、m、m D.1m、2m、3m、4m
5.对于函数y=(k<0),下列说法错误的是( )
A.它的图象分布在二、四象限
B.它的图象既是轴对称图形又是中心对称图形
C.当x>0时,y的值随x的增大而增大
D.当x<0时,y的值随x的增大而减小
6.在比例尺为1:2000000的地图上,相距5cm的两地,它们的实际距离为( )
A.10km B.100km C.500km D.1000km
7.若点A(﹣3,y1)、B(﹣1,y2)、C(3,y3)都在反比例函数y=(k>0)的图象上,则y1、y2、y3的大小关系是( )
A.y1>y2>y3 B.y3>y1>y2 C.y2>y1>y3 D.y1>y3>y2
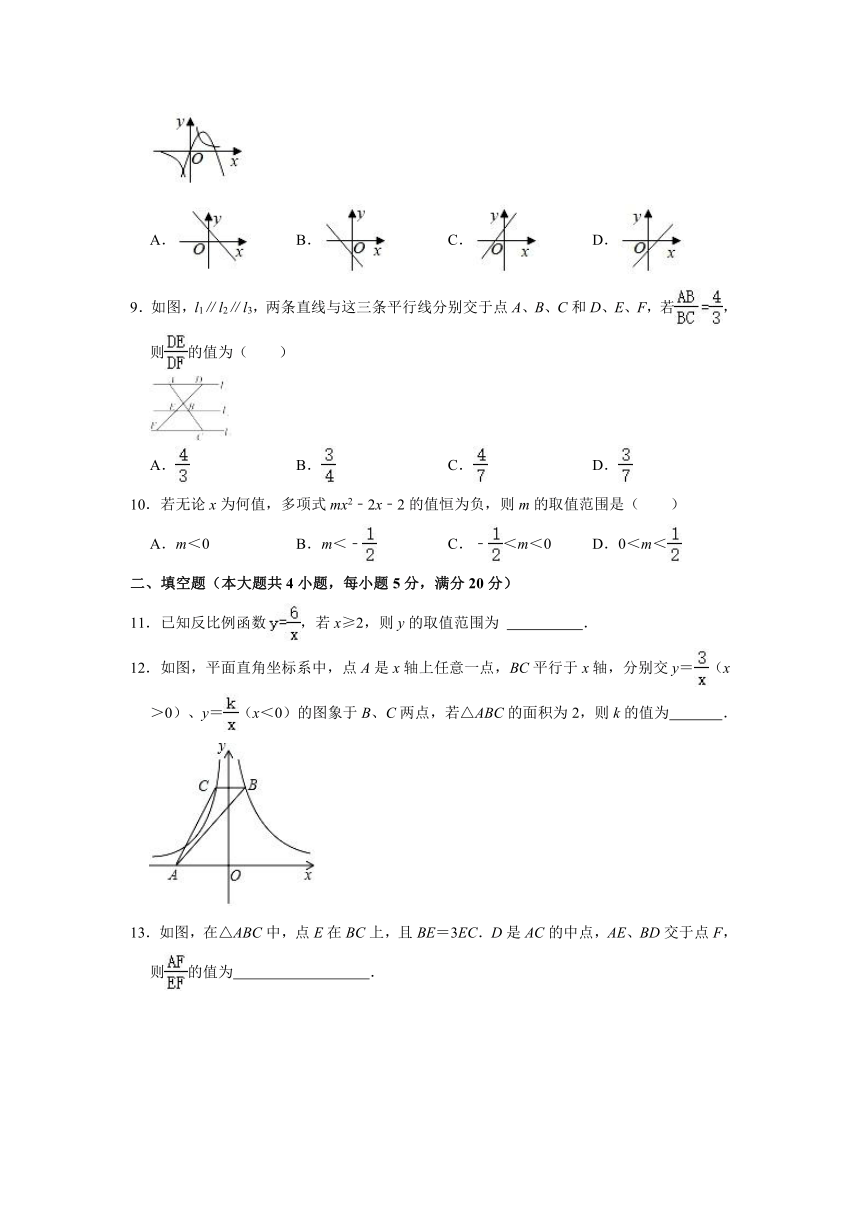
8.已知在同一直角坐标系中二次函数y=mx2+nx和反比例函数y=的图象如图所示,则一次函数y=x﹣n的图象可能是( )
A. B. C. D.
9.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F,若,则的值为( )
A. B. C. D.
10.若无论x为何值,多项式mx2﹣2x﹣2的值恒为负,则m的取值范围是( )
A.m<0 B.m<﹣ C.﹣<m<0 D.0<m<
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知反比例函数,若x≥2,则y的取值范围为 .
12.如图,平面直角坐标系中,点A是x轴上任意一点,BC平行于x轴,分别交y=(x>0)、y=(x<0)的图象于B、C两点,若△ABC的面积为2,则k的值为 .
13.如图,在△ABC中,点E在BC上,且BE=3EC.D是AC的中点,AE、BD交于点F,则的值为 .
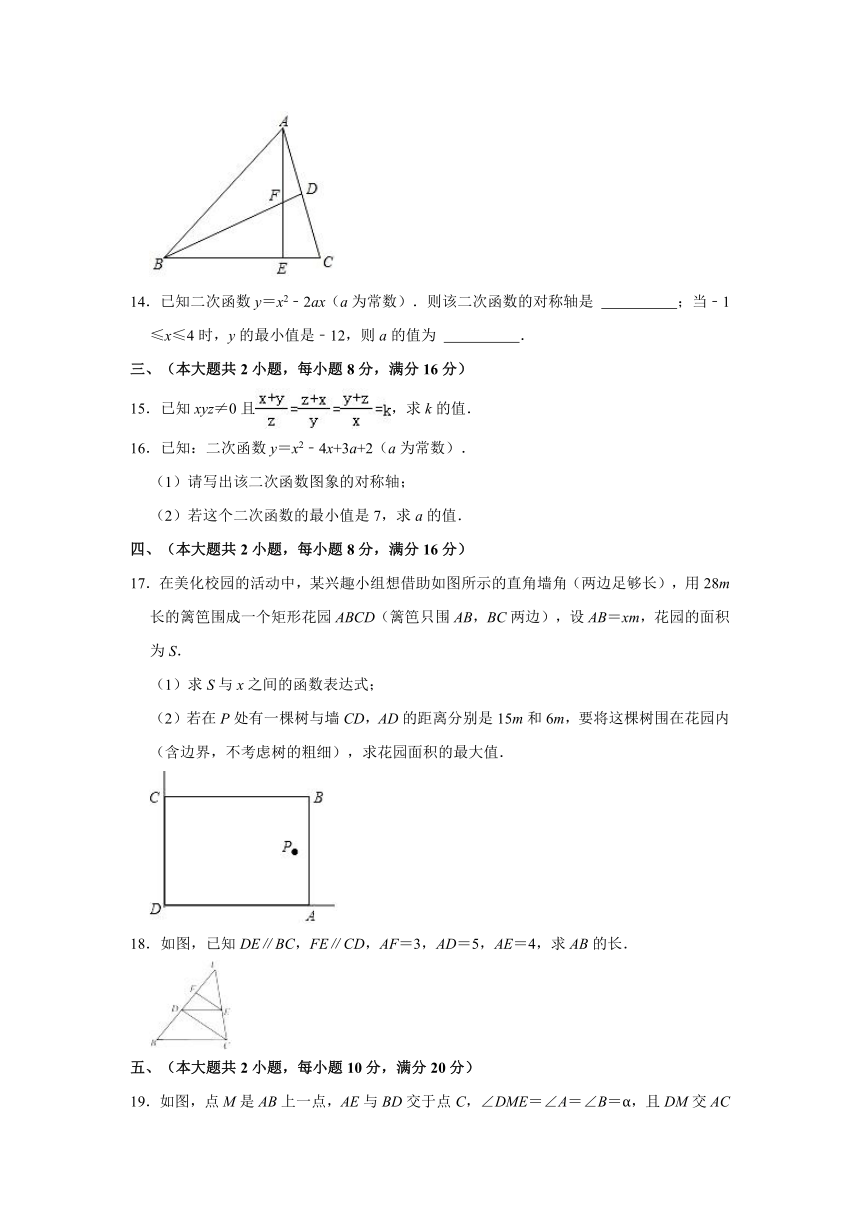
14.已知二次函数y=x2﹣2ax(a为常数).则该二次函数的对称轴是 ;当﹣1≤x≤4时,y的最小值是﹣12,则a的值为 .
三、(本大题共2小题,每小题8分,满分16分)
15.已知xyz≠0且,求k的值.
16.已知:二次函数y=x2﹣4x+3a+2(a为常数).
(1)请写出该二次函数图象的对称轴;
(2)若这个二次函数的最小值是7,求a的值.
四、(本大题共2小题,每小题8分,满分16分)
17.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm,花园的面积为S.
(1)求S与x之间的函数表达式;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积的最大值.
18.如图,已知DE∥BC,FE∥CD,AF=3,AD=5,AE=4,求AB的长.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,点M是AB上一点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.
(1)求证:△AMF∽△BGM;
(2)请你再写出两对相似三角形.
20.如图是抛物线型拱桥,当拱顶离水面8米时,水面宽AB为12米.当水面上升6米时达到警戒水位,此时拱桥内的水面宽度是多少米?下面是两个兴趣小组解决这个问题的两种方法,请补充完整:
方法一:如图1,以点A为原点,AB所在直线为x轴,建立平面直角坐标系xOy,此时点B的坐标为 ,抛物线的顶点坐标为 ,可求这条抛物线的解析式为 .
方法二:如图2,以抛物线顶点为原点,对称轴为y轴,建立平面直角坐标系xOy,这时这条抛物线所表示的二次函数的解析式为 .当取y=﹣2时,即可求出此时拱桥内的水面宽度为 ,解决了这个问题.
六、(本题满分12分)
21.如图,在直角坐标系中,点A(3,a)和点B是一次函数y=x﹣2和反比例函数y=图象的交点.
(1)求反比例函数的表达式和点B的坐标.
(2)利用图象,直接写出当x﹣2>时x的取值范围.
(3)C为线段AB上一点,且横坐标为正,作CD∥y轴与反比例函数y=交于点D,当△BCD的面积最大时,则C点的坐标为 .
七、(本题满分12分)
22.已知抛物线y1=ax2+bx+c的顶点A是直线y2=2x与y3=﹣2x+4的交点,且经过直线y3=﹣2x+4与y轴的交点B.
(1)求点A的坐标;
(2)求抛物线的表达式;
(3)写出当y1>y3时x的取值范围.
八、(本题满分14分)
23.某超市拟于中秋节前50天里销售某品牌月饼,其进价为18元/kg.设第x天的销售价格为y(元/kg),销售量为m(kg).该超市根据以往的销售经验得出以下的销售规律:①当1≤x≤30时,y=40;当31≤x≤50时,y与x满足一次函数关系,且当=36时,y=37;x=44时,y=33.②m与x的关系为m=5x+50.
(1)当31≤x≤50时,求y与x的关系式;
(2)x为多少时,当天的销售利润W(元)最大?最大利润为多少?
(3)若超市希望第31天到第35天的日销售利润W(元)随x的增大而增大,则需要在当天销售价格的基础上涨a元/kg,求a的取值范围.
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
1.将抛物线y=﹣2x2﹣3向左平移4个单位,再向上平移1个单位所得新抛物线的表达式为( )
A.y=﹣2(x﹣4)2﹣4 B.y=﹣2(x+4)2﹣2
C.y=﹣2x2+4 D.y=﹣2x2+4
【分析】根据平移的规律:左加右减,上加下减解答.
解:将抛物线y=﹣2x2﹣3向左平移4个单位,再向上平移1个单位所得新抛物线的表达式为y=﹣2(x+4)2﹣3+1,即y=﹣2(x+4)2﹣2.
故选:B.
2.把二次函数y=x2+4x﹣3化成y=a(x+h)2+k的形式,正确的是( )
A.y=(x+2)2﹣7 B.y=(x﹣2)2+7 C.y=(x﹣2)2﹣7 D.y=(x+2)2+1
【分析】利用配方法整理即可得解.
解:y=x2+4x﹣3
=x2+4x+4﹣7
=(x+2)2﹣7,
故选:A.
3.对于二次函数y=﹣(x+2)2+3的图象,下列说法正确的是( )
A.开口向上 B.当x=2时,y有最小值是3
C.对称轴是x=2 D.顶点坐标是(﹣2,3)
【分析】直接由顶点式得到对称轴、开口方向、顶点坐标和最值.
解:由y=﹣(x+2)2+3得,开口向下,对称轴为直线x=﹣2,顶点坐标为(﹣2,3),当x=﹣2时,y有最大值是3,
故选项A、B、C错误,选项D正确;
故选:D.
4.下列四组线段中,成比例线段的有( )
A.1m、2m、3m、6dm B.2m、4m、9m、18cm
C.1m、m、m、m D.1m、2m、3m、4m
【分析】如果其中两条线段的比(即它们的长度比)与另两条线段的比相等,则四条线段叫成比例线段.根据比例性质对选项一一分析,排除错误答案.
解:A、1×0.6≠2×3,故选项不符合题意;
B、2×0.18≠4×9,故选项不符合题意;
C、1×=,故选项符合题意;
D、1×4≠2×3,故选项不符合题意.
故选:C.
5.对于函数y=(k<0),下列说法错误的是( )
A.它的图象分布在二、四象限
B.它的图象既是轴对称图形又是中心对称图形
C.当x>0时,y的值随x的增大而增大
D.当x<0时,y的值随x的增大而减小
【分析】根据反比例函y=的性质:当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大,图象既是轴对称图形又是中心对称图形进行判断即可.
解:A、它的图象分布在二、四象限,说法正确,不符合题意;
B、它的图象既是轴对称图形又是中心对称图形,说法正确,不符合题意;
C、当x>0时,y的值随x的增大而增大,说法正确,不符合题意;
D、当x<0时,y的值随x的增大而减大,说法错误,符合题意;
故选:D.
6.在比例尺为1:2000000的地图上,相距5cm的两地,它们的实际距离为( )
A.10km B.100km C.500km D.1000km
【分析】根据图上距离除以比例尺,算出实际距离,进而把cm换算成km即可.
解:5÷=10000000(cm),
10000000cm=100km.
故选:B.
7.若点A(﹣3,y1)、B(﹣1,y2)、C(3,y3)都在反比例函数y=(k>0)的图象上,则y1、y2、y3的大小关系是( )
A.y1>y2>y3 B.y3>y1>y2 C.y2>y1>y3 D.y1>y3>y2
【分析】先根据反比例函数中k>0判断出函数图象所在的象限及增减性,再根据各点横坐标的特点即可得出结论.
解:∵反比例函数y=中k>0,
∴函数图象的两个分支分别位于一、三象限,且在每一象限内y随x的增大而减小.
∵﹣3<﹣1<0,
∴点A(﹣3,y1),B(﹣1,y2)位于第三象限,
∴y2<y1<0,
∵3>0,
∴点C(3,y3)位于第一象限,
∴y3>0,
∴y3>y1>y2.
故选:B.
8.已知在同一直角坐标系中二次函数y=mx2+nx和反比例函数y=的图象如图所示,则一次函数y=x﹣n的图象可能是( )
A. B. C. D.
【分析】根据反比例函数图象和二次函数图象经过的象限,即可得出m<0、n>0、a>0,由此即可得出<0,﹣n<0,即可得出一次函数y=x﹣n的图象经过二三四象限,再对照四个选项中的图象即可得出结论.
解:∵二次函数开口向下,
∴m<0;
∵二次函数的对称轴在y轴右侧,左同右异,
∴b符号与a相异,n>0;
∵反比例函数图象经过一三象限,
∴a>0,
∴<0,﹣n<0,
∴一次函数y=x﹣n的图象经过二三四象限.
故选:B.
9.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F,若,则的值为( )
A. B. C. D.
【分析】直接利用平行线分线段成比例定理进而得出,再将已知数据代入求出即可.
解:∵l1∥l2∥l3,
∴=,
∵,
∴=,
∴=.
故选:C.
10.若无论x为何值,多项式mx2﹣2x﹣2的值恒为负,则m的取值范围是( )
A.m<0 B.m<﹣ C.﹣<m<0 D.0<m<
【分析】设y=mx2﹣2x﹣2,函数值恒为负,则抛物线开口向下,且抛物线与x轴没有交点,得出关于m的不等式组,求解即可得出m的取值范围.
解:设y=mx2﹣2x﹣2,
∵函数值恒为负,
∴,
解得:m<,
故选:B.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知反比例函数,若x≥2,则y的取值范围为 0<y≤3 .
【分析】求得x=2时的函数值,然后根据反比例函数的性质即可得到y的取值范围.
解:∵反比例函数中,k=6>0,
∴图象在第一、三象限,且在每个象限y随x的增大而减小,
∵当x=2时,y=3,
∴当x≥2时,0<y≤3.
故答案:0<y≤3.
12.如图,平面直角坐标系中,点A是x轴上任意一点,BC平行于x轴,分别交y=(x>0)、y=(x<0)的图象于B、C两点,若△ABC的面积为2,则k的值为 ﹣1 .
【分析】连接OC、OB,如图,由于BC∥x轴,根据三角形面积公式得到S△ACB=S△OCB,再利用反比例函数系数k的几何意义得到 |3|+ |k|=2,然后解关于k的绝对值方程可得到满足条件的k的值.
解:连接OC、OB,如图,
∵BC∥x轴,
∴S△ACB=S△OCB,
而S△OCB= |3|+ |k|,
∴ |3|+ |k|=2,
而k<0,
∴k=﹣1.
故答案为:﹣1.
13.如图,在△ABC中,点E在BC上,且BE=3EC.D是AC的中点,AE、BD交于点F,则的值为 .
【分析】过E点作EH∥AC交BD于H,如图,根据平行线分线段成比例定理,由EH∥CD得到=,由于AD=CD,则=,然后利用EH∥AD,根据平行线分线段成比例定理得的值.
解:过E点作EH∥AC交BD于H,如图,
∵EH∥CD,
∴=,
∵BE=3EC,
∴==,
∵D是AC的中点,
∴AD=CD,
∴=,
∵EH∥AD,
∴==.
故答案为.
14.已知二次函数y=x2﹣2ax(a为常数).则该二次函数的对称轴是 直线x=a ;当﹣1≤x≤4时,y的最小值是﹣12,则a的值为 2或﹣6.5 .
【分析】把函数解析式化成顶点式即可求得对称轴,然后利用分类讨论的数学方法可以求得a的值.
解:∵y=x2﹣2ax=(x﹣a)2﹣a2,
∴该二次函数的对称轴是直线x=a,
∵当﹣1≤x≤4时,y的最小值是﹣12,
∴当a>4时,x=4取得最小值,则﹣12=(4﹣a)2﹣a2,解得,a=3.5(舍去),
当﹣1≤a≤4时,x=a取得最小值,则﹣12=(a﹣a)2﹣a2,解得,a=2,
当a<﹣1时,x=﹣1取得最小值,则﹣12=(﹣1﹣a)2﹣a2,解得,a=﹣6.5,
故答案为:直线x=a,2或﹣6.5.
三、(本大题共2小题,每小题8分,满分16分)
15.已知xyz≠0且,求k的值.
【分析】分①当x+y+z≠0时,利用等比性质解答,②当x+y+z=0时,用一个字母表示出另两个字母的和,然后求解即可.
解:∵xyz≠0,
∴x、y、z均不为0,
①当x+y+z≠0时,∵===k,
∴k==2,
②当x+y+z=0时,x+y=﹣z,z+x=﹣y,y+z=﹣x,
所以,k=﹣1,
综上所述,k=2或﹣1.
16.已知:二次函数y=x2﹣4x+3a+2(a为常数).
(1)请写出该二次函数图象的对称轴;
(2)若这个二次函数的最小值是7,求a的值.
【分析】(1)由x=﹣求得对称轴;
(2)将对称轴的x值代入函数解析式求得函数的最小值,然后求出a的值;
解:(1)对称轴为直线x=﹣=﹣=2.
(2)当x=2时,y最小值=22﹣4×2+3a+2=4﹣8+3a+2=3a﹣2,
∵最小值是7,
∴3a﹣2=7,
解得:a=3.
四、(本大题共2小题,每小题8分,满分16分)
17.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm,花园的面积为S.
(1)求S与x之间的函数表达式;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积的最大值.
【分析】(1)根据长方形的面积公式可得S关于x的函数解析式;
(2)由树与墙CD,AD的距离分别是15m和6m求出x的取值范围,再结合二次函数的性质可得答案.
解:(1)∵AB=xm,
∴BC=(28﹣x)m.
则S=AB BC=x(28﹣x)=﹣x2+28x.
即S=﹣x2+28x(0<x<28).
(2)由题意可知,,
解得6≤x≤13.
由(1)知,S=﹣x2+28x=﹣(x﹣14)2+196.
∵当6≤x≤13时,S随x的增大而增大,
∴当x=13时,S最大值=195,
即花园面积的最大值为195m2.
18.如图,已知DE∥BC,FE∥CD,AF=3,AD=5,AE=4,求AB的长.
【分析】根据平行线分线段成比例定理列出比例式,代入计算即可.
解:∵FE∥CD,
∴=,即=,
解得,AC=,
∵DE∥BC,
∴=,即=,
解得,AB=.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,点M是AB上一点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.
(1)求证:△AMF∽△BGM;
(2)请你再写出两对相似三角形.
【分析】(1)根据两角对应相等的两个三角形相似证明即可.
(2)根据相似三角形的判定解决问题即可.
【解答】(1)证明:∵∠DME=∠A=∠B=α,
∴∠AMF+∠BMG=180°﹣α,
∵∠A+∠AMF+∠AFM=180°,
∴∠AMF+∠AFM=180°﹣α,
∴∠AFM=∠BMG,
∴△AMF∽△BGM;
(2)解:∵∠D=∠D,∠DMG=∠DBM.
∴△DMG∽△DBM,
同法可证:△EMF∽△EAM.
20.如图是抛物线型拱桥,当拱顶离水面8米时,水面宽AB为12米.当水面上升6米时达到警戒水位,此时拱桥内的水面宽度是多少米?下面是两个兴趣小组解决这个问题的两种方法,请补充完整:
方法一:如图1,以点A为原点,AB所在直线为x轴,建立平面直角坐标系xOy,此时点B的坐标为 (12,0) ,抛物线的顶点坐标为 (6,8) ,可求这条抛物线的解析式为 y=﹣x2+ .
方法二:如图2,以抛物线顶点为原点,对称轴为y轴,建立平面直角坐标系xOy,这时这条抛物线所表示的二次函数的解析式为 y=﹣x2 .当取y=﹣2时,即可求出此时拱桥内的水面宽度为 6米 ,解决了这个问题.
【分析】方法一:根据已知条件得到B(12,0),顶点(6,8),设二次函数的解析式为y=a(x﹣6)2+8,把B点的坐标代入解方程即可得到结论;
方法二:设抛物线解析式为y=ax2,将点(6,﹣8)代入求得a的值,据此可得抛物线的解析式,再求y=﹣2时x的值从而求出水面宽.
解:方法一:A(0,0),B(12,0),顶点(6,8),
设二次函数的解析式为y=a(x﹣6)2+8,
把B点的坐标代入得,a=﹣,
∴y=﹣(x﹣6)2+8=﹣x2+,
∴二次函数的解析式为y=﹣x2+.
故答案为:(12,0);(6,8)y=﹣x2+x;
方法二:设二次函数的解析式为y=ax2,
把B(6,﹣8)代入得,a=﹣,
∴二次函数的解析式为y=﹣x2;
当y=﹣2时,﹣2=﹣x2,
解得:x=±3,
即可求出此时拱桥内的水面宽度为6米.
故答案为:y=﹣x2;6米.
六、(本题满分12分)
21.如图,在直角坐标系中,点A(3,a)和点B是一次函数y=x﹣2和反比例函数y=图象的交点.
(1)求反比例函数的表达式和点B的坐标.
(2)利用图象,直接写出当x﹣2>时x的取值范围.
(3)C为线段AB上一点,且横坐标为正,作CD∥y轴与反比例函数y=交于点D,当△BCD的面积最大时,则C点的坐标为 (1,﹣1) .
【分析】(1)由一次函数y=x﹣2求得A的坐标,然后根据待定系数法求得反比例函数的解析式,解析式联立成方程组,解方程组求得B的坐标;
(2)根据图象即可求得;
(3)设C(x,x﹣2)(x>0),则D(x,),求得CD=﹣x+2,由三角形面积公式可得S△BCD=x (﹣x+2)=﹣(x﹣1)2+2,所以当x=1时,△BCD的面积最大,此时,C的坐标为(1,﹣1).
解:(1)把A(3,a)代入y=x﹣2可得,
a=1,即A(3,1),
∴1=,解得m=3,
∴反比例函数表达式为y=,
解,得或,
∴B(﹣1,﹣3);
(2)由图象可得,
当x﹣2>时,﹣1<x<0或x>3;
(3)设C(x,x﹣2)(x>0),则D(x,),
∴CD=﹣x+2,
∴S△BCD=x (﹣x+2)=﹣(x﹣1)2+2,
∴当x=1时,△BCD的面积最大,此时,C的坐标为(1,﹣1).
故答案为:(1,﹣1).
七、(本题满分12分)
22.已知抛物线y1=ax2+bx+c的顶点A是直线y2=2x与y3=﹣2x+4的交点,且经过直线y3=﹣2x+4与y轴的交点B.
(1)求点A的坐标;
(2)求抛物线的表达式;
(3)写出当y1>y3时x的取值范围.
【分析】(1)y2=2x与y3=﹣2x+4联立,组成方程组,解方程组即可求得;
(2)根据待定系数法即可求得;
(3)根据二次函数的性质,结合A、B的坐标即可求得.
解:(1)解得,
∴A(1,2);
(2)在直线y3=﹣2x+4中,令x=0,则y=4,
∴B(0,4),
设抛物线的解析式为y=a(x﹣1)2+2,
代入B(0,4)得,4=a+2,
解得a=2,
∴抛物线的表达式为y=2(x﹣1)2+2=2x2﹣4x+4;
(3)∵抛物线与直线y3=﹣2x+4的交点为A(1,2),B(0,4),
∴当y1>y3时x的取值范围是x<0或x>1.
八、(本题满分14分)
23.某超市拟于中秋节前50天里销售某品牌月饼,其进价为18元/kg.设第x天的销售价格为y(元/kg),销售量为m(kg).该超市根据以往的销售经验得出以下的销售规律:①当1≤x≤30时,y=40;当31≤x≤50时,y与x满足一次函数关系,且当=36时,y=37;x=44时,y=33.②m与x的关系为m=5x+50.
(1)当31≤x≤50时,求y与x的关系式;
(2)x为多少时,当天的销售利润W(元)最大?最大利润为多少?
(3)若超市希望第31天到第35天的日销售利润W(元)随x的增大而增大,则需要在当天销售价格的基础上涨a元/kg,求a的取值范围.
【分析】(1)依据题意利用待定系数法,易得出当31≤x≤50时,y与x的关系式为:y=﹣x+55.
(2)根据销售利润=销售量×(售价﹣进价),列出每天的销售利润w(元)与销售价x(元/kg)之间的函数关系式,再依据函数的增减性求得最大利润.
(3)要使第31天到第35天的日销售利润W(元)随x的增大而增大,则对称轴=﹣>34.5,求得a即可.
解:(1)依题意,当x=36时,y=37;x=44时,y=33,
当31≤x≤50时,设y=kx+b,
则有,
解得,
∴y与x的关系式为:y=﹣x+55.
(2)依题意,
∵W=(y﹣18) m,
∴W=,
整理得,W=,
当1≤x≤30时,
∵W随x增大而增大,
∴x=30时,取最大值W=30×110+1100=4400,
当31≤x≤50时,
W=x2+160x+1850=﹣(x﹣32)2+4410,
∵﹣<0,
∴x=32时,W取得最大值,此时W=4410,
综上所述,x为32时,当天的销售利润W(元)最大,最大利润为4410元.
(3)依题意,得,
W=(y+a﹣18) m=﹣x2+(160+5a)x+1850+50a,
∵第31天到第35天的日销售利润W(元)随x的增大而增大,
∴对称轴x=﹣=﹣≥34.5,得a≥2.5,
故a的取值范围为a≥2.5.
一、选择题(本大题共10小题,每小题4分,满分40分)
1.将抛物线y=﹣2x2﹣3向左平移4个单位,再向上平移1个单位所得新抛物线的表达式为( )
A.y=﹣2(x﹣4)2﹣4 B.y=﹣2(x+4)2﹣2
C.y=﹣2x2+4 D.y=﹣2x2+4
2.把二次函数y=x2+4x﹣3化成y=a(x+h)2+k的形式,正确的是( )
A.y=(x+2)2﹣7 B.y=(x﹣2)2+7 C.y=(x﹣2)2﹣7 D.y=(x+2)2+1
3.对于二次函数y=﹣(x+2)2+3的图象,下列说法正确的是( )
A.开口向上 B.当x=2时,y有最小值是3
C.对称轴是x=2 D.顶点坐标是(﹣2,3)
4.下列四组线段中,成比例线段的有( )
A.1m、2m、3m、6dm B.2m、4m、9m、18cm
C.1m、m、m、m D.1m、2m、3m、4m
5.对于函数y=(k<0),下列说法错误的是( )
A.它的图象分布在二、四象限
B.它的图象既是轴对称图形又是中心对称图形
C.当x>0时,y的值随x的增大而增大
D.当x<0时,y的值随x的增大而减小
6.在比例尺为1:2000000的地图上,相距5cm的两地,它们的实际距离为( )
A.10km B.100km C.500km D.1000km
7.若点A(﹣3,y1)、B(﹣1,y2)、C(3,y3)都在反比例函数y=(k>0)的图象上,则y1、y2、y3的大小关系是( )
A.y1>y2>y3 B.y3>y1>y2 C.y2>y1>y3 D.y1>y3>y2
8.已知在同一直角坐标系中二次函数y=mx2+nx和反比例函数y=的图象如图所示,则一次函数y=x﹣n的图象可能是( )
A. B. C. D.
9.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F,若,则的值为( )
A. B. C. D.
10.若无论x为何值,多项式mx2﹣2x﹣2的值恒为负,则m的取值范围是( )
A.m<0 B.m<﹣ C.﹣<m<0 D.0<m<
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知反比例函数,若x≥2,则y的取值范围为 .
12.如图,平面直角坐标系中,点A是x轴上任意一点,BC平行于x轴,分别交y=(x>0)、y=(x<0)的图象于B、C两点,若△ABC的面积为2,则k的值为 .
13.如图,在△ABC中,点E在BC上,且BE=3EC.D是AC的中点,AE、BD交于点F,则的值为 .
14.已知二次函数y=x2﹣2ax(a为常数).则该二次函数的对称轴是 ;当﹣1≤x≤4时,y的最小值是﹣12,则a的值为 .
三、(本大题共2小题,每小题8分,满分16分)
15.已知xyz≠0且,求k的值.
16.已知:二次函数y=x2﹣4x+3a+2(a为常数).
(1)请写出该二次函数图象的对称轴;
(2)若这个二次函数的最小值是7,求a的值.
四、(本大题共2小题,每小题8分,满分16分)
17.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm,花园的面积为S.
(1)求S与x之间的函数表达式;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积的最大值.
18.如图,已知DE∥BC,FE∥CD,AF=3,AD=5,AE=4,求AB的长.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,点M是AB上一点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.
(1)求证:△AMF∽△BGM;
(2)请你再写出两对相似三角形.
20.如图是抛物线型拱桥,当拱顶离水面8米时,水面宽AB为12米.当水面上升6米时达到警戒水位,此时拱桥内的水面宽度是多少米?下面是两个兴趣小组解决这个问题的两种方法,请补充完整:
方法一:如图1,以点A为原点,AB所在直线为x轴,建立平面直角坐标系xOy,此时点B的坐标为 ,抛物线的顶点坐标为 ,可求这条抛物线的解析式为 .
方法二:如图2,以抛物线顶点为原点,对称轴为y轴,建立平面直角坐标系xOy,这时这条抛物线所表示的二次函数的解析式为 .当取y=﹣2时,即可求出此时拱桥内的水面宽度为 ,解决了这个问题.
六、(本题满分12分)
21.如图,在直角坐标系中,点A(3,a)和点B是一次函数y=x﹣2和反比例函数y=图象的交点.
(1)求反比例函数的表达式和点B的坐标.
(2)利用图象,直接写出当x﹣2>时x的取值范围.
(3)C为线段AB上一点,且横坐标为正,作CD∥y轴与反比例函数y=交于点D,当△BCD的面积最大时,则C点的坐标为 .
七、(本题满分12分)
22.已知抛物线y1=ax2+bx+c的顶点A是直线y2=2x与y3=﹣2x+4的交点,且经过直线y3=﹣2x+4与y轴的交点B.
(1)求点A的坐标;
(2)求抛物线的表达式;
(3)写出当y1>y3时x的取值范围.
八、(本题满分14分)
23.某超市拟于中秋节前50天里销售某品牌月饼,其进价为18元/kg.设第x天的销售价格为y(元/kg),销售量为m(kg).该超市根据以往的销售经验得出以下的销售规律:①当1≤x≤30时,y=40;当31≤x≤50时,y与x满足一次函数关系,且当=36时,y=37;x=44时,y=33.②m与x的关系为m=5x+50.
(1)当31≤x≤50时,求y与x的关系式;
(2)x为多少时,当天的销售利润W(元)最大?最大利润为多少?
(3)若超市希望第31天到第35天的日销售利润W(元)随x的增大而增大,则需要在当天销售价格的基础上涨a元/kg,求a的取值范围.
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
1.将抛物线y=﹣2x2﹣3向左平移4个单位,再向上平移1个单位所得新抛物线的表达式为( )
A.y=﹣2(x﹣4)2﹣4 B.y=﹣2(x+4)2﹣2
C.y=﹣2x2+4 D.y=﹣2x2+4
【分析】根据平移的规律:左加右减,上加下减解答.
解:将抛物线y=﹣2x2﹣3向左平移4个单位,再向上平移1个单位所得新抛物线的表达式为y=﹣2(x+4)2﹣3+1,即y=﹣2(x+4)2﹣2.
故选:B.
2.把二次函数y=x2+4x﹣3化成y=a(x+h)2+k的形式,正确的是( )
A.y=(x+2)2﹣7 B.y=(x﹣2)2+7 C.y=(x﹣2)2﹣7 D.y=(x+2)2+1
【分析】利用配方法整理即可得解.
解:y=x2+4x﹣3
=x2+4x+4﹣7
=(x+2)2﹣7,
故选:A.
3.对于二次函数y=﹣(x+2)2+3的图象,下列说法正确的是( )
A.开口向上 B.当x=2时,y有最小值是3
C.对称轴是x=2 D.顶点坐标是(﹣2,3)
【分析】直接由顶点式得到对称轴、开口方向、顶点坐标和最值.
解:由y=﹣(x+2)2+3得,开口向下,对称轴为直线x=﹣2,顶点坐标为(﹣2,3),当x=﹣2时,y有最大值是3,
故选项A、B、C错误,选项D正确;
故选:D.
4.下列四组线段中,成比例线段的有( )
A.1m、2m、3m、6dm B.2m、4m、9m、18cm
C.1m、m、m、m D.1m、2m、3m、4m
【分析】如果其中两条线段的比(即它们的长度比)与另两条线段的比相等,则四条线段叫成比例线段.根据比例性质对选项一一分析,排除错误答案.
解:A、1×0.6≠2×3,故选项不符合题意;
B、2×0.18≠4×9,故选项不符合题意;
C、1×=,故选项符合题意;
D、1×4≠2×3,故选项不符合题意.
故选:C.
5.对于函数y=(k<0),下列说法错误的是( )
A.它的图象分布在二、四象限
B.它的图象既是轴对称图形又是中心对称图形
C.当x>0时,y的值随x的增大而增大
D.当x<0时,y的值随x的增大而减小
【分析】根据反比例函y=的性质:当k<0,双曲线的两支分别位于第二、第四象限,在每一象限内y随x的增大而增大,图象既是轴对称图形又是中心对称图形进行判断即可.
解:A、它的图象分布在二、四象限,说法正确,不符合题意;
B、它的图象既是轴对称图形又是中心对称图形,说法正确,不符合题意;
C、当x>0时,y的值随x的增大而增大,说法正确,不符合题意;
D、当x<0时,y的值随x的增大而减大,说法错误,符合题意;
故选:D.
6.在比例尺为1:2000000的地图上,相距5cm的两地,它们的实际距离为( )
A.10km B.100km C.500km D.1000km
【分析】根据图上距离除以比例尺,算出实际距离,进而把cm换算成km即可.
解:5÷=10000000(cm),
10000000cm=100km.
故选:B.
7.若点A(﹣3,y1)、B(﹣1,y2)、C(3,y3)都在反比例函数y=(k>0)的图象上,则y1、y2、y3的大小关系是( )
A.y1>y2>y3 B.y3>y1>y2 C.y2>y1>y3 D.y1>y3>y2
【分析】先根据反比例函数中k>0判断出函数图象所在的象限及增减性,再根据各点横坐标的特点即可得出结论.
解:∵反比例函数y=中k>0,
∴函数图象的两个分支分别位于一、三象限,且在每一象限内y随x的增大而减小.
∵﹣3<﹣1<0,
∴点A(﹣3,y1),B(﹣1,y2)位于第三象限,
∴y2<y1<0,
∵3>0,
∴点C(3,y3)位于第一象限,
∴y3>0,
∴y3>y1>y2.
故选:B.
8.已知在同一直角坐标系中二次函数y=mx2+nx和反比例函数y=的图象如图所示,则一次函数y=x﹣n的图象可能是( )
A. B. C. D.
【分析】根据反比例函数图象和二次函数图象经过的象限,即可得出m<0、n>0、a>0,由此即可得出<0,﹣n<0,即可得出一次函数y=x﹣n的图象经过二三四象限,再对照四个选项中的图象即可得出结论.
解:∵二次函数开口向下,
∴m<0;
∵二次函数的对称轴在y轴右侧,左同右异,
∴b符号与a相异,n>0;
∵反比例函数图象经过一三象限,
∴a>0,
∴<0,﹣n<0,
∴一次函数y=x﹣n的图象经过二三四象限.
故选:B.
9.如图,l1∥l2∥l3,两条直线与这三条平行线分别交于点A、B、C和D、E、F,若,则的值为( )
A. B. C. D.
【分析】直接利用平行线分线段成比例定理进而得出,再将已知数据代入求出即可.
解:∵l1∥l2∥l3,
∴=,
∵,
∴=,
∴=.
故选:C.
10.若无论x为何值,多项式mx2﹣2x﹣2的值恒为负,则m的取值范围是( )
A.m<0 B.m<﹣ C.﹣<m<0 D.0<m<
【分析】设y=mx2﹣2x﹣2,函数值恒为负,则抛物线开口向下,且抛物线与x轴没有交点,得出关于m的不等式组,求解即可得出m的取值范围.
解:设y=mx2﹣2x﹣2,
∵函数值恒为负,
∴,
解得:m<,
故选:B.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知反比例函数,若x≥2,则y的取值范围为 0<y≤3 .
【分析】求得x=2时的函数值,然后根据反比例函数的性质即可得到y的取值范围.
解:∵反比例函数中,k=6>0,
∴图象在第一、三象限,且在每个象限y随x的增大而减小,
∵当x=2时,y=3,
∴当x≥2时,0<y≤3.
故答案:0<y≤3.
12.如图,平面直角坐标系中,点A是x轴上任意一点,BC平行于x轴,分别交y=(x>0)、y=(x<0)的图象于B、C两点,若△ABC的面积为2,则k的值为 ﹣1 .
【分析】连接OC、OB,如图,由于BC∥x轴,根据三角形面积公式得到S△ACB=S△OCB,再利用反比例函数系数k的几何意义得到 |3|+ |k|=2,然后解关于k的绝对值方程可得到满足条件的k的值.
解:连接OC、OB,如图,
∵BC∥x轴,
∴S△ACB=S△OCB,
而S△OCB= |3|+ |k|,
∴ |3|+ |k|=2,
而k<0,
∴k=﹣1.
故答案为:﹣1.
13.如图,在△ABC中,点E在BC上,且BE=3EC.D是AC的中点,AE、BD交于点F,则的值为 .
【分析】过E点作EH∥AC交BD于H,如图,根据平行线分线段成比例定理,由EH∥CD得到=,由于AD=CD,则=,然后利用EH∥AD,根据平行线分线段成比例定理得的值.
解:过E点作EH∥AC交BD于H,如图,
∵EH∥CD,
∴=,
∵BE=3EC,
∴==,
∵D是AC的中点,
∴AD=CD,
∴=,
∵EH∥AD,
∴==.
故答案为.
14.已知二次函数y=x2﹣2ax(a为常数).则该二次函数的对称轴是 直线x=a ;当﹣1≤x≤4时,y的最小值是﹣12,则a的值为 2或﹣6.5 .
【分析】把函数解析式化成顶点式即可求得对称轴,然后利用分类讨论的数学方法可以求得a的值.
解:∵y=x2﹣2ax=(x﹣a)2﹣a2,
∴该二次函数的对称轴是直线x=a,
∵当﹣1≤x≤4时,y的最小值是﹣12,
∴当a>4时,x=4取得最小值,则﹣12=(4﹣a)2﹣a2,解得,a=3.5(舍去),
当﹣1≤a≤4时,x=a取得最小值,则﹣12=(a﹣a)2﹣a2,解得,a=2,
当a<﹣1时,x=﹣1取得最小值,则﹣12=(﹣1﹣a)2﹣a2,解得,a=﹣6.5,
故答案为:直线x=a,2或﹣6.5.
三、(本大题共2小题,每小题8分,满分16分)
15.已知xyz≠0且,求k的值.
【分析】分①当x+y+z≠0时,利用等比性质解答,②当x+y+z=0时,用一个字母表示出另两个字母的和,然后求解即可.
解:∵xyz≠0,
∴x、y、z均不为0,
①当x+y+z≠0时,∵===k,
∴k==2,
②当x+y+z=0时,x+y=﹣z,z+x=﹣y,y+z=﹣x,
所以,k=﹣1,
综上所述,k=2或﹣1.
16.已知:二次函数y=x2﹣4x+3a+2(a为常数).
(1)请写出该二次函数图象的对称轴;
(2)若这个二次函数的最小值是7,求a的值.
【分析】(1)由x=﹣求得对称轴;
(2)将对称轴的x值代入函数解析式求得函数的最小值,然后求出a的值;
解:(1)对称轴为直线x=﹣=﹣=2.
(2)当x=2时,y最小值=22﹣4×2+3a+2=4﹣8+3a+2=3a﹣2,
∵最小值是7,
∴3a﹣2=7,
解得:a=3.
四、(本大题共2小题,每小题8分,满分16分)
17.在美化校园的活动中,某兴趣小组想借助如图所示的直角墙角(两边足够长),用28m长的篱笆围成一个矩形花园ABCD(篱笆只围AB,BC两边),设AB=xm,花园的面积为S.
(1)求S与x之间的函数表达式;
(2)若在P处有一棵树与墙CD,AD的距离分别是15m和6m,要将这棵树围在花园内(含边界,不考虑树的粗细),求花园面积的最大值.
【分析】(1)根据长方形的面积公式可得S关于x的函数解析式;
(2)由树与墙CD,AD的距离分别是15m和6m求出x的取值范围,再结合二次函数的性质可得答案.
解:(1)∵AB=xm,
∴BC=(28﹣x)m.
则S=AB BC=x(28﹣x)=﹣x2+28x.
即S=﹣x2+28x(0<x<28).
(2)由题意可知,,
解得6≤x≤13.
由(1)知,S=﹣x2+28x=﹣(x﹣14)2+196.
∵当6≤x≤13时,S随x的增大而增大,
∴当x=13时,S最大值=195,
即花园面积的最大值为195m2.
18.如图,已知DE∥BC,FE∥CD,AF=3,AD=5,AE=4,求AB的长.
【分析】根据平行线分线段成比例定理列出比例式,代入计算即可.
解:∵FE∥CD,
∴=,即=,
解得,AC=,
∵DE∥BC,
∴=,即=,
解得,AB=.
五、(本大题共2小题,每小题10分,满分20分)
19.如图,点M是AB上一点,AE与BD交于点C,∠DME=∠A=∠B=α,且DM交AC于F,ME交BC于G.
(1)求证:△AMF∽△BGM;
(2)请你再写出两对相似三角形.
【分析】(1)根据两角对应相等的两个三角形相似证明即可.
(2)根据相似三角形的判定解决问题即可.
【解答】(1)证明:∵∠DME=∠A=∠B=α,
∴∠AMF+∠BMG=180°﹣α,
∵∠A+∠AMF+∠AFM=180°,
∴∠AMF+∠AFM=180°﹣α,
∴∠AFM=∠BMG,
∴△AMF∽△BGM;
(2)解:∵∠D=∠D,∠DMG=∠DBM.
∴△DMG∽△DBM,
同法可证:△EMF∽△EAM.
20.如图是抛物线型拱桥,当拱顶离水面8米时,水面宽AB为12米.当水面上升6米时达到警戒水位,此时拱桥内的水面宽度是多少米?下面是两个兴趣小组解决这个问题的两种方法,请补充完整:
方法一:如图1,以点A为原点,AB所在直线为x轴,建立平面直角坐标系xOy,此时点B的坐标为 (12,0) ,抛物线的顶点坐标为 (6,8) ,可求这条抛物线的解析式为 y=﹣x2+ .
方法二:如图2,以抛物线顶点为原点,对称轴为y轴,建立平面直角坐标系xOy,这时这条抛物线所表示的二次函数的解析式为 y=﹣x2 .当取y=﹣2时,即可求出此时拱桥内的水面宽度为 6米 ,解决了这个问题.
【分析】方法一:根据已知条件得到B(12,0),顶点(6,8),设二次函数的解析式为y=a(x﹣6)2+8,把B点的坐标代入解方程即可得到结论;
方法二:设抛物线解析式为y=ax2,将点(6,﹣8)代入求得a的值,据此可得抛物线的解析式,再求y=﹣2时x的值从而求出水面宽.
解:方法一:A(0,0),B(12,0),顶点(6,8),
设二次函数的解析式为y=a(x﹣6)2+8,
把B点的坐标代入得,a=﹣,
∴y=﹣(x﹣6)2+8=﹣x2+,
∴二次函数的解析式为y=﹣x2+.
故答案为:(12,0);(6,8)y=﹣x2+x;
方法二:设二次函数的解析式为y=ax2,
把B(6,﹣8)代入得,a=﹣,
∴二次函数的解析式为y=﹣x2;
当y=﹣2时,﹣2=﹣x2,
解得:x=±3,
即可求出此时拱桥内的水面宽度为6米.
故答案为:y=﹣x2;6米.
六、(本题满分12分)
21.如图,在直角坐标系中,点A(3,a)和点B是一次函数y=x﹣2和反比例函数y=图象的交点.
(1)求反比例函数的表达式和点B的坐标.
(2)利用图象,直接写出当x﹣2>时x的取值范围.
(3)C为线段AB上一点,且横坐标为正,作CD∥y轴与反比例函数y=交于点D,当△BCD的面积最大时,则C点的坐标为 (1,﹣1) .
【分析】(1)由一次函数y=x﹣2求得A的坐标,然后根据待定系数法求得反比例函数的解析式,解析式联立成方程组,解方程组求得B的坐标;
(2)根据图象即可求得;
(3)设C(x,x﹣2)(x>0),则D(x,),求得CD=﹣x+2,由三角形面积公式可得S△BCD=x (﹣x+2)=﹣(x﹣1)2+2,所以当x=1时,△BCD的面积最大,此时,C的坐标为(1,﹣1).
解:(1)把A(3,a)代入y=x﹣2可得,
a=1,即A(3,1),
∴1=,解得m=3,
∴反比例函数表达式为y=,
解,得或,
∴B(﹣1,﹣3);
(2)由图象可得,
当x﹣2>时,﹣1<x<0或x>3;
(3)设C(x,x﹣2)(x>0),则D(x,),
∴CD=﹣x+2,
∴S△BCD=x (﹣x+2)=﹣(x﹣1)2+2,
∴当x=1时,△BCD的面积最大,此时,C的坐标为(1,﹣1).
故答案为:(1,﹣1).
七、(本题满分12分)
22.已知抛物线y1=ax2+bx+c的顶点A是直线y2=2x与y3=﹣2x+4的交点,且经过直线y3=﹣2x+4与y轴的交点B.
(1)求点A的坐标;
(2)求抛物线的表达式;
(3)写出当y1>y3时x的取值范围.
【分析】(1)y2=2x与y3=﹣2x+4联立,组成方程组,解方程组即可求得;
(2)根据待定系数法即可求得;
(3)根据二次函数的性质,结合A、B的坐标即可求得.
解:(1)解得,
∴A(1,2);
(2)在直线y3=﹣2x+4中,令x=0,则y=4,
∴B(0,4),
设抛物线的解析式为y=a(x﹣1)2+2,
代入B(0,4)得,4=a+2,
解得a=2,
∴抛物线的表达式为y=2(x﹣1)2+2=2x2﹣4x+4;
(3)∵抛物线与直线y3=﹣2x+4的交点为A(1,2),B(0,4),
∴当y1>y3时x的取值范围是x<0或x>1.
八、(本题满分14分)
23.某超市拟于中秋节前50天里销售某品牌月饼,其进价为18元/kg.设第x天的销售价格为y(元/kg),销售量为m(kg).该超市根据以往的销售经验得出以下的销售规律:①当1≤x≤30时,y=40;当31≤x≤50时,y与x满足一次函数关系,且当=36时,y=37;x=44时,y=33.②m与x的关系为m=5x+50.
(1)当31≤x≤50时,求y与x的关系式;
(2)x为多少时,当天的销售利润W(元)最大?最大利润为多少?
(3)若超市希望第31天到第35天的日销售利润W(元)随x的增大而增大,则需要在当天销售价格的基础上涨a元/kg,求a的取值范围.
【分析】(1)依据题意利用待定系数法,易得出当31≤x≤50时,y与x的关系式为:y=﹣x+55.
(2)根据销售利润=销售量×(售价﹣进价),列出每天的销售利润w(元)与销售价x(元/kg)之间的函数关系式,再依据函数的增减性求得最大利润.
(3)要使第31天到第35天的日销售利润W(元)随x的增大而增大,则对称轴=﹣>34.5,求得a即可.
解:(1)依题意,当x=36时,y=37;x=44时,y=33,
当31≤x≤50时,设y=kx+b,
则有,
解得,
∴y与x的关系式为:y=﹣x+55.
(2)依题意,
∵W=(y﹣18) m,
∴W=,
整理得,W=,
当1≤x≤30时,
∵W随x增大而增大,
∴x=30时,取最大值W=30×110+1100=4400,
当31≤x≤50时,
W=x2+160x+1850=﹣(x﹣32)2+4410,
∵﹣<0,
∴x=32时,W取得最大值,此时W=4410,
综上所述,x为32时,当天的销售利润W(元)最大,最大利润为4410元.
(3)依题意,得,
W=(y+a﹣18) m=﹣x2+(160+5a)x+1850+50a,
∵第31天到第35天的日销售利润W(元)随x的增大而增大,
∴对称轴x=﹣=﹣≥34.5,得a≥2.5,
故a的取值范围为a≥2.5.
同课章节目录
