2021-2022学年安徽省合肥五十中新校九年级(上)期中数学试卷(Word版 含解析)
文档属性
| 名称 | 2021-2022学年安徽省合肥五十中新校九年级(上)期中数学试卷(Word版 含解析) |

|
|
| 格式 | doc | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 00:00:00 | ||
图片预览



文档简介
2021-2022学年安徽省合肥五十中新校九年级第一学期期中数学试卷
一、选择题(本大题共10小题,每小题4分,满分40分)
1.已知y=(m+2)x|m|+2是关于x的二次函数,那么m的值为( )
A.﹣2 B.2 C.±2 D.0
2.抛物线y=﹣3(x+1)2﹣2经过平移得到抛物线y=﹣3x2,平移方法是( )
A.向左平移1个单位,再向下平移2个单位
B.向左平移1个单位,再向上平移2个单位
C.向右平移1个单位,再向下平移2个单位
D.向右平移1个单位,再向上平移2个单位
3.二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为( )
A.3 B.﹣3 C. D.﹣
4.大自然巧夺天工,一片小枫树叶,也蕴含着“黄金分割”.如图,P为AB的黄金分割点(AP>PB),如果AP的长度为8,那么AB的长度是( )
A.4﹣4 B.12﹣4 C.12+4 D.4+4
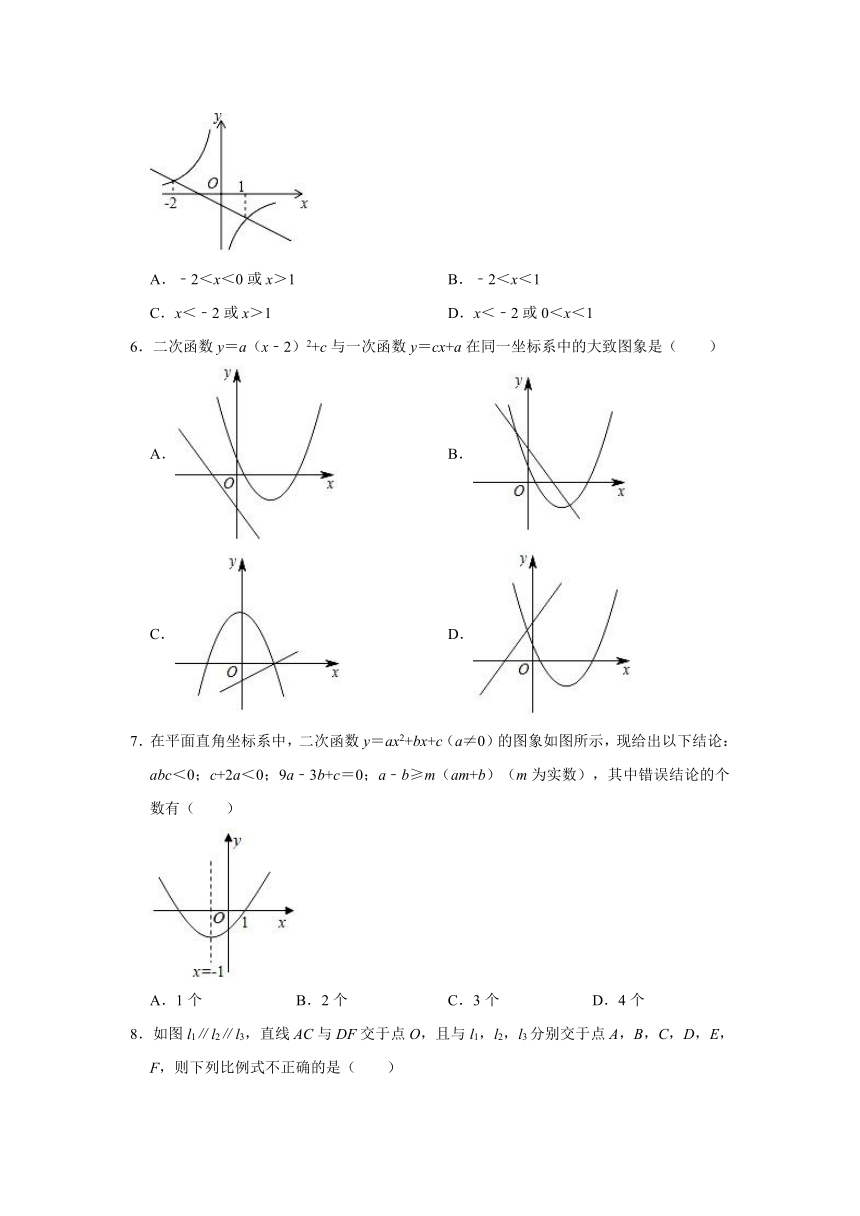
5.一次函数y1=k1x+b和反比例函数y2=(k1 k2≠0)的图象如图所示,若y1>y2,则x的取值范围是( )
A.﹣2<x<0或x>1 B.﹣2<x<1
C.x<﹣2或x>1 D.x<﹣2或0<x<1
6.二次函数y=a(x﹣2)2+c与一次函数y=cx+a在同一坐标系中的大致图象是( )
A. B.
C. D.
7.在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给出以下结论:abc<0;c+2a<0;9a﹣3b+c=0;a﹣b≥m(am+b)(m为实数),其中错误结论的个数有( )
A.1个 B.2个 C.3个 D.4个
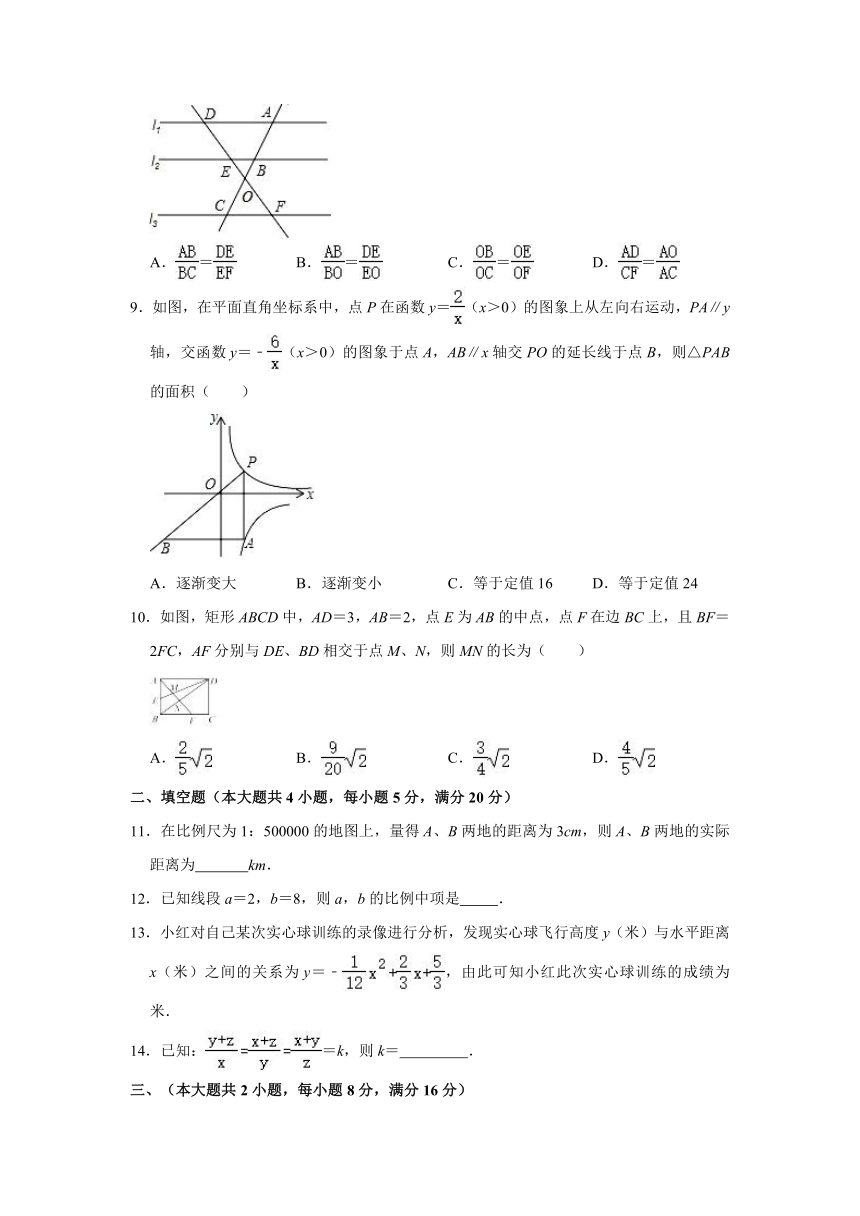
8.如图l1∥l2∥l3,直线AC与DF交于点O,且与l1,l2,l3分别交于点A,B,C,D,E,F,则下列比例式不正确的是( )
A.= B.= C.= D.=
9.如图,在平面直角坐标系中,点P在函数y=(x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣(x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )
A.逐渐变大 B.逐渐变小 C.等于定值16 D.等于定值24
10.如图,矩形ABCD中,AD=3,AB=2,点E为AB的中点,点F在边BC上,且BF=2FC,AF分别与DE、BD相交于点M、N,则MN的长为( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.在比例尺为1:500000的地图上,量得A、B两地的距离为3cm,则A、B两地的实际距离为 km.
12.已知线段a=2,b=8,则a,b的比例中项是 .
13.小红对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系为y=﹣,由此可知小红此次实心球训练的成绩为 米.
14.已知:=k,则k= .
三、(本大题共2小题,每小题8分,满分16分)
15.已知a、b、c是△ABC的三边,且满足==,a+b+c=12,试判断△ABC的形状,并说明理由.
16.已知抛物线y=﹣x2+bx+c过点(0,﹣3)和(2,1).
(1)试确定抛物线的解析式;
(2)求出抛物线与x轴的交点坐标和顶点坐标;
(3)画出函数图象、写出当y>0的x的取值范围.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,E是平行四边形ABCD的边BA延长线上一点,连接EC,交AD于F.
(1)写出图中的三对相似三角形(注意:不添加辅助线);
(2)请在你所找出的相似三角形中选一对,说明相似的理由.
18.如图:一次函数y=ax+b的图象与反比例函数y=的图象交于A(2,m)、B(﹣1,﹣4)两点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象直接写出,当x为何值时,ax+b﹣>0.
五、(本大题共2小题,每小题10分,满分20分)
19.为了预防流感,某学校用药熏消毒法对教室进行消毒.已知一瓶药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
(1)写出倾倒一瓶药物后,从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量不低于8毫克时,消毒有效,那么倾倒一瓶药物后,从药物释放开始,有效消毒时间是多少分钟?
20.如图,抛物线y=x2﹣bx+3与x轴相交于点A,B,且过点C(4,3).
(1)求b的值和该抛物线顶点P的坐标;
(2)将该抛物线向左平移,记平移后抛物线的顶点为P′,当四边形AP′PB为平行四边形时,求平移后抛物线的解析式.
六、(本题满分12分)
21.如图,在Rt△ABC中,∠A=90°,AB=8,AC=6.若动点D从点B出发,沿线段BA运动到点A为止,运动速度为每秒2个单位长度.过点D作DE∥BC交AC于点E,设动点D运动的时间为x秒,AE的长为y.
(1)求出y关于x的函数关系式,并写出自变量x的取值范围;
(2)求出△BDE的面积S与x之间的函数关系式;
(3)当x为何值时,△BDE的面积S有最大值,最大值为多少?
七、(本题满分12分)
22.某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额﹣生产费用)
(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,求今年可获得最大毛利润
八、(本题满分14分)
23.直线y=x﹣2与x、y轴分别交于点A、C.抛物线的图象经过A、C和点B(1,0).
(1)求抛物线的解析式和顶点G的坐标;
(2)在直线y=﹣1上是否存在点P,使得△PBG的周长最小?若存在,求出P点的坐标;若不存在,请说明理由.
(3)在直线AC上方的抛物线上有一动点D,当D与直线AC的距离DE最大时,求出点D的坐标,并求出最大距离是多少?
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
1.已知y=(m+2)x|m|+2是关于x的二次函数,那么m的值为( )
A.﹣2 B.2 C.±2 D.0
【分析】根据形如y=ax2+bx+c (a≠0)是二次函数,可得答案.
解:∵y=(m+2)x|m|+2是y关于x的二次函数,
∴|m|=2且m+2≠0.
解得m=2.
故选:B.
2.抛物线y=﹣3(x+1)2﹣2经过平移得到抛物线y=﹣3x2,平移方法是( )
A.向左平移1个单位,再向下平移2个单位
B.向左平移1个单位,再向上平移2个单位
C.向右平移1个单位,再向下平移2个单位
D.向右平移1个单位,再向上平移2个单位
【分析】由抛物线y=﹣3(x+1)2﹣2得到顶点坐标为(﹣1,﹣2),而平移后抛物线y=﹣3x2的顶点坐标为(0,0),根据顶点坐标的变化寻找平移方法.
解:∵抛物线y=﹣3(x+1)2﹣2的顶点坐标为(﹣1,﹣2),
平移后抛物线y=﹣3x2的顶点坐标为(0,0),
∴平移方法为:向右平移1个单位,再向上平移2个单位.
故选:D.
3.二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为( )
A.3 B.﹣3 C. D.﹣
【分析】根据函数图象中的数据,可以得到该函数的最小值,再根据一元二次方程ax2+bx+m=0有实数根,从而可以求得m的取值范围,从而可以得到m的最大值.
解:由图象可得,
二次函数y=ax2+bx的最小值是y=﹣3,
∵一元二次方程ax2+bx+m=0有实数根,
即一元二次方程ax2+bx=﹣m有实数根,
也就是y=ax2+bx与y=﹣m有交点,
∴﹣m≥﹣3,
解得:m≤3,
∴m的最大值是3,
故选:A.
4.大自然巧夺天工,一片小枫树叶,也蕴含着“黄金分割”.如图,P为AB的黄金分割点(AP>PB),如果AP的长度为8,那么AB的长度是( )
A.4﹣4 B.12﹣4 C.12+4 D.4+4
【分析】根据黄金分割的定义得到AP=AB,然后把AP的长度代入可求出AB的长.
解:∵P为AB的黄金分割点(AP>PB),
∴AP=AB,
∴AB=AP=×8=4+4,
故选:D.
5.一次函数y1=k1x+b和反比例函数y2=(k1 k2≠0)的图象如图所示,若y1>y2,则x的取值范围是( )
A.﹣2<x<0或x>1 B.﹣2<x<1
C.x<﹣2或x>1 D.x<﹣2或0<x<1
【分析】直接利用两函数图象的交点横坐标得出y1>y2时,x的取值范围.
解:如图所示:
若y1>y2,则x的取值范围是:x<﹣2或0<x<1.
故选:D.
6.二次函数y=a(x﹣2)2+c与一次函数y=cx+a在同一坐标系中的大致图象是( )
A. B.
C. D.
【分析】可先根据一次函数的图象判断a、b的符号,再判断二次函数图象与实际是否相符,判断正误.
解:A、一次函数y=cx+a的图象与y轴交于负半轴,a<0,与二次函数y=a(x﹣2)2+c的图象开口向上,即a>0相矛盾,故A错误;
B、一次函数y=cx+a的图象过一、二、四象限,a>0,c<0,二次函数y=a(x﹣2)2+c的图象开口向上,顶点为(2,c)在第四象限,a>0,c<0,故B正确;
C、二次函数y=a(x﹣2)2+c的对称轴x=2,在y轴右侧,故C错误;
D、一次函数y=cx+a的图象过一、二、三象限,c>0,与抛物线y=a(x﹣2)2+c的顶点(2,c)在第四象限,c<0相矛盾,故D错误;
故选:B.
7.在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给出以下结论:abc<0;c+2a<0;9a﹣3b+c=0;a﹣b≥m(am+b)(m为实数),其中错误结论的个数有( )
A.1个 B.2个 C.3个 D.4个
【分析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解:由抛物线可知:a>0,c<0,
对称轴x=﹣<0,
∴b>0,
∴abc<0;
由对称轴可知:﹣=﹣1,
∴b=2a,
∵x=1时,y=a+b+c=0,
∴c+3a=0,
∴c+2a=﹣3a+2a=﹣a<0;
(1,0)关于x=﹣1的对称点为(﹣3,0),
∴x=﹣3时,y=9a﹣3b+c=0;
当x=﹣1时,y的最小值为a﹣b+c,
∴x=m时,y=am2+bm+c,
∴am2+bm+c≥a﹣b+c,
即a﹣b≤m(am+b);
∴错误的为a﹣b≥m(am+b),有1个.
故选:A.
8.如图l1∥l2∥l3,直线AC与DF交于点O,且与l1,l2,l3分别交于点A,B,C,D,E,F,则下列比例式不正确的是( )
A.= B.= C.= D.=
【分析】平行线分线段成比例定理的内容是:一组平行线截两条直线,所截的线段对应成比例,根据以上内容判断即可.
解:A、∵l1∥l2∥l3,
∴=,故本选项错误;
B、∵l1∥l2∥l3,
∴=,故本选项错误;
C、∵l1∥l2∥l3,
∴=,故本选项错误;
D、∵l1∥l2∥l3,
∴=,故本选项正确;
故选:D.
9.如图,在平面直角坐标系中,点P在函数y=(x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣(x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )
A.逐渐变大 B.逐渐变小 C.等于定值16 D.等于定值24
【分析】根据反比例函数k的几何意义得出S△POC=×2=1,S矩形ACOD=6,即可得出=,从而得出=,通过证得
△POC∽△PBA,得出=()2=,即可得出S△PAB=16S△POC=16.
解:由题意可知S△POC=×2=1,S矩形ACOD=6,
∵S△POC=OC PC,S矩形ACOD=OC AC,
∴==,
∴=,
∴=,
∵AB∥x轴,
∴△POC∽△PBA,
∴=()2=,
∴S△PAB=16S△POC=16,
∴△PAB的面积等于定值16.
故选:C.
10.如图,矩形ABCD中,AD=3,AB=2,点E为AB的中点,点F在边BC上,且BF=2FC,AF分别与DE、BD相交于点M、N,则MN的长为( )
A. B. C. D.
【分析】过点F作FH⊥AD于H,交ED于O,得FH=AB=2,由勾股定理得AF=2,根据平行线分线段成比例得OH=,由相似三角形的性质得,求得AM,再根据相似三角形的性质求得AN=,即可得出结果.
解:如图,过点F作FH⊥AD于H,交ED于O,
则FH=AB=2,
∵BF=2FC,
∴BF=AH=2,FC=HD=1,
∴AF==2,
∵OH∥AE,
∴,
∴OF=FH﹣OH=2﹣=,
∵AE∥FO,
∴△AME∽△FMO,
∴,
∴AM=,
∵AD∥BF,
∴△AND∽△FNB,
∴,
∴AN=,
∴MN=AN﹣AM==,
故选:B.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.在比例尺为1:500000的地图上,量得A、B两地的距离为3cm,则A、B两地的实际距离为 15 km.
【分析】由在比例尺为1:50000的地图上,量得A、B两地的图上距离AB=3cm,根据比例尺的定义,可求得两地的实际距离.
解:∵比例尺为1:500000,量得两地的距离是3厘米,
∴A、B两地的实际距离3×500000=1500000cm=15km,
故答案为15.
12.已知线段a=2,b=8,则a,b的比例中项是 4 .
【分析】设线段a,b的比例中项为c,根据比例中项的定义可知,c2=ab,代入数据可直接求得c的值,注意两条线段的比例中项为正数.
解:设线段a,b的比例中项为c,
∵c是长度分别为2、8的两条线段的比例中项,
∴c2=ab=2×8,
即c2=16,
∴c=4(负数舍去).
故答案为:4.
13.小红对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系为y=﹣,由此可知小红此次实心球训练的成绩为 10 米.
【分析】根据铅球落地时,高度y=0,把实际问题可理解为当y=0时,求x的值即可.
解:当y=0时,y=﹣x2+x+=0,
解得:x1=﹣2(舍去),x2=10,
∴小红此次实心球训练的成绩为10米.
故答案为:10.
14.已知:=k,则k= 2或﹣1 .
【分析】能够根据比例的基本性质熟练进行比例式和等积式的互相转换.
解:此题要分情况考虑:
当x+y+z≠0时,则根据比例的等比性质,得k==2;
当x+y+z=0时,即x+y=﹣z,则k=﹣1,故填2或﹣1.
三、(本大题共2小题,每小题8分,满分16分)
15.已知a、b、c是△ABC的三边,且满足==,a+b+c=12,试判断△ABC的形状,并说明理由.
【分析】设===k,表示a、b、c的长,代入a+b+c=12中,计算k的值,可得三边的长,根据勾股定理的逆定理可得结论.
解:△ABC是直角三角形,理由是:
设===k,
则a=3k﹣4,b=2k﹣3,c=4k﹣8,
∵a+b+c=12,
∴3k﹣4+2k﹣3+4k﹣8=12,
∴k=3,
∴a=5,b=3,c=4,
∴b2+c2=32+42=25=a2,
∴△ABC是直角三角形.
16.已知抛物线y=﹣x2+bx+c过点(0,﹣3)和(2,1).
(1)试确定抛物线的解析式;
(2)求出抛物线与x轴的交点坐标和顶点坐标;
(3)画出函数图象、写出当y>0的x的取值范围.
【分析】(1)把(0,﹣3)和(2,1)代入抛物线,得出方程组,求出方程组的解,即可得出抛物线的解析式;
(2)把y=0代入解析式,求出x的值,即可得出抛物线与x轴的交点坐标,把抛物线解析式改写成顶点式即可;
(3)根据函数解析式,列表,描点,画图,根据图象即可求出当y>0时x的取值范围.
解:(1)∵抛物线y=﹣x2+bx+c过点(0,﹣3)和(2,1),
∴,
解得 ,
抛物线的解析式为y=﹣x2+4x﹣3;
(2)令y=0,得﹣x2+4x﹣3=0,即 x2﹣4x+3=0,
∴x1=1,x2=3,
∴抛物线与x轴的交点坐标为(1,0)、(3,0),
∵抛物线的解析式为y=﹣x2+4x﹣3=﹣(x﹣2)2+1,
∴顶点坐标为:(2,1);
(3)列表:
画图:
由图象可知,当y>0时,1<x<3.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,E是平行四边形ABCD的边BA延长线上一点,连接EC,交AD于F.
(1)写出图中的三对相似三角形(注意:不添加辅助线);
(2)请在你所找出的相似三角形中选一对,说明相似的理由.
【分析】(1)证明△EAF∽△EBC,△CDF∽△EBC,△CDF∽△EAF即可;
(2)根据平行线定理可求得∠EAF=∠B,进而可以求证△EAF∽△EBC即可解题.
解:(1)△EAF∽△EBC,△CDF∽△EBC,△CDF∽△EAF.
(2)选△EAF∽△EBC,
理由如下:在ABCD中AD∥BC,
∴∠EAF=∠B.
又∵∠E=∠E,
∴△EAF∽△EBC.
18.如图:一次函数y=ax+b的图象与反比例函数y=的图象交于A(2,m)、B(﹣1,﹣4)两点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象直接写出,当x为何值时,ax+b﹣>0.
【分析】(1)把点B坐标代入反比例函数求解析式,然后求出点A坐标,再将A,B坐标代入一次函数解析式求解.
(2)设直线AB与y轴交于点C,由S△AOB=S△BOC+S△AOC求解.
(3)由ax+b﹣>0得ax+b>,再根据图象交点横坐标求解.
解:(1)把(﹣1,﹣4)代入y=中得﹣4=,
解得k=4,
∴反比例函数解析式为y=,
把(2,m)代入y=中得m==2,
∴点A坐标为(2,2)
把(﹣1,﹣4),(2,2)代入y=ax+b得,
解得,
∴一次函数解析式为y=2x﹣2.
(2)设直线AB与y轴交于点C,
把x=0代入y=2x﹣2得y=﹣2,
∴OC=2.
∴S△AOB=S△BOC+S△AOC=×OC |xB|+×OC xA=×2×1+2×2=3.
(3)由ax+b﹣>0得ax+b>,
∵直线与双曲线交点为A(2,2)、B(﹣1,﹣4),
∴﹣1<x<0或x>2时ax+b>.
五、(本大题共2小题,每小题10分,满分20分)
19.为了预防流感,某学校用药熏消毒法对教室进行消毒.已知一瓶药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
(1)写出倾倒一瓶药物后,从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量不低于8毫克时,消毒有效,那么倾倒一瓶药物后,从药物释放开始,有效消毒时间是多少分钟?
【分析】(1)根据函数图象找出点的坐标,再根据点的坐标利用待定系数法即可求出一次函数和反比例函数的关系式;
(2)将y=8分别代入两函数关系式中求出x值,二者做差即可得出结论.
解:(1)当0≤x≤15时,设y=ax(a≠0);当x≥15时,设y=(k≠0).
将(15,20)代入y=ax,
20=15a,解得:a=,
∴y=x(0≤x≤15).
将(15,20)代入y=,
20=,解得:k=300,
∴y=(x≥15).
(2)当y=x=8时,x=6;
当y==8时,x=37.5.
37.5﹣6=31.5(分钟).
答:有效消毒时间是31.5分钟.
20.如图,抛物线y=x2﹣bx+3与x轴相交于点A,B,且过点C(4,3).
(1)求b的值和该抛物线顶点P的坐标;
(2)将该抛物线向左平移,记平移后抛物线的顶点为P′,当四边形AP′PB为平行四边形时,求平移后抛物线的解析式.
【分析】(1)根据抛物线y=x2﹣bx+3过点C(4,3),代入求出b的值即可,再利用配方法求出顶点坐标即可;
(2)首先求出AB的长,再根据四边形AP′PB为平行四边形,得出P′P=AB=2,进而得出P′的坐标,求出解析式即可.
解:(1)当x=4,y=3,代入y=x2﹣bx+3,
解得:b=4,
∴y=x2﹣4x+3=(x﹣2)2﹣1,
∴b的值为4,和该抛物线顶点P的坐标为:(2,﹣1);
(2)当y=0时,x2﹣4x+3=0,
解得:x1=1,x2=3,
∴AB=2,
∵四边形AP′PB为平行四边形,
∴P′P=AB=2,
∴P′的坐标是(0,﹣1),
∴抛物线的解析式是:y=x2﹣1.
六、(本题满分12分)
21.如图,在Rt△ABC中,∠A=90°,AB=8,AC=6.若动点D从点B出发,沿线段BA运动到点A为止,运动速度为每秒2个单位长度.过点D作DE∥BC交AC于点E,设动点D运动的时间为x秒,AE的长为y.
(1)求出y关于x的函数关系式,并写出自变量x的取值范围;
(2)求出△BDE的面积S与x之间的函数关系式;
(3)当x为何值时,△BDE的面积S有最大值,最大值为多少?
【分析】(1)由平行线得△ABC∽△ADE,根据相似形的性质得关系式;
(2)s= BD AE;
(3)运用函数性质求解.
解:(1)∵DE∥BC,
∴△ADE∽△ABC.
∴.
又∵AD=8﹣2x,AB=8,AE=y,AC=6,
∴.
∴.
自变量x的取值范围为0≤x≤4.
(2)S=BD AE= 2x y
=﹣x2+6x
(3)S=﹣x2+6x
=﹣x2+6x+9﹣9
=﹣(x﹣2)2+6.
∴当x=2时,S有最大值,且最大值为6.
七、(本题满分12分)
22.某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额﹣生产费用)
(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,求今年可获得最大毛利润
【分析】(1)利用待定系数法可求出y与x以及z与x之间的函数关系式;
(2)根据(1)的表达式及毛利润=销售额﹣生产费用,可得出w与x之间的函数关系式;
(3)首先求出x的取值范围,再利用二次函数增减性得出答案即可.
解:(1)图①可得函数经过点(100,1000),
设抛物线的解析式为y=ax2(a≠0),
将点(100,1000)代入得:1000=10000a,
解得:a=,
故y与x之间的关系式为y=x2,
图②可得:函数经过点(0,30)、(100,20),
设z=kx+b,则,
解得:,
故z与x之间的关系式为z=﹣x+30;
(2)w=zx﹣y
=﹣x2+30x﹣x2
=﹣x2+30x,
∴w与x之间的函数关系式为w=﹣x2+30x;
(3)令y=360,得x2=360,
解得:x=±60(负值舍去),
由图象可知,当0<y≤360时,0<x≤60,
w=﹣x2+30x
=﹣(x2﹣150x)
=﹣(x﹣75)2+1125,
∵﹣<0,
∴当x≤75时,w随x的增大而增大,
∵0<x≤60,
∴当x=60时,w有最大值,最大值为﹣(60﹣75)2+1125=1080,
答:今年最多可获得毛利润1080万元.
八、(本题满分14分)
23.直线y=x﹣2与x、y轴分别交于点A、C.抛物线的图象经过A、C和点B(1,0).
(1)求抛物线的解析式和顶点G的坐标;
(2)在直线y=﹣1上是否存在点P,使得△PBG的周长最小?若存在,求出P点的坐标;若不存在,请说明理由.
(3)在直线AC上方的抛物线上有一动点D,当D与直线AC的距离DE最大时,求出点D的坐标,并求出最大距离是多少?
【分析】(1)用待定系数法即可求解;
(2)作点B关于直线y=﹣1的对称点H(1,﹣2),连接GH交直线y=﹣1于点P,在点P为所求点,进而求解;
(3)由S△ACD=S梯形AGFC﹣S△CDF﹣S△ADG=(AG+FC) FG﹣FC FD﹣DG AG,即可求解.
解:(1)在直线解析式y=x﹣2中,令x=0,得y=﹣2;令y=0,得x=4,
∴A(4,0),C(0,﹣2).
设抛物线的解析式为y=ax2+bx+c,
∵点A(4,0),B(1,0),C(0,﹣2)在抛物线上,
则,解得,
∴抛物线的解析式为:y=﹣x2+x﹣2;
抛物线的对称轴为x=,当x=时,y=﹣x2+x﹣2=,故点G(,);
(2)在直线y=﹣1上存在点P,使得使得△PBG的周长最小,
作点B关于直线y=﹣1的对称点H(1,﹣2),连接GH交直线y=﹣1于点P,在点P为所求点,
理由:△PBG的周长=BG+BP+PG=BG+PH+PG=GH+GB为最小,
由点BG的坐标得,直线BG的表达式为y=x﹣,
当y=1=x﹣,解得x=,
故点P的坐标为(,﹣1);
(3)设点D坐标为(x,y),则y=﹣x2+x﹣2,
在Rt△AOC中,OA=4,OC=2,由勾股定理得:AC=2.
连接CD、AD,过点D作DF⊥y轴于点F,过点A作AG⊥FD交FD的延长线于点G,
则FD=x,DG=4﹣x,OF=AG=y,FC=y+2.
S△ACD=S梯形AGFC﹣S△CDF﹣S△ADG=(AG+FC) FG﹣FC FD﹣DG AG=(y+y+2)×4﹣(y+2) x﹣(4﹣x) y=2y﹣x+4,
将y=﹣x2+x﹣2代入得:S△ACD=2y﹣x+4=﹣x2+4x=﹣(x﹣2)2+4,
∴当x=2时,△ACD的面积最大,最大值为4.
当x=2时,y=1,∴D(2,1).
∵S△ACD=AC DE,AC=2,
∴当△ACD的面积最大时,高DE最大,
则DE的最大值为:.
∴当D与直线AC的距离DE最大时,点D的坐标为(2,1),最大距离为.
一、选择题(本大题共10小题,每小题4分,满分40分)
1.已知y=(m+2)x|m|+2是关于x的二次函数,那么m的值为( )
A.﹣2 B.2 C.±2 D.0
2.抛物线y=﹣3(x+1)2﹣2经过平移得到抛物线y=﹣3x2,平移方法是( )
A.向左平移1个单位,再向下平移2个单位
B.向左平移1个单位,再向上平移2个单位
C.向右平移1个单位,再向下平移2个单位
D.向右平移1个单位,再向上平移2个单位
3.二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为( )
A.3 B.﹣3 C. D.﹣
4.大自然巧夺天工,一片小枫树叶,也蕴含着“黄金分割”.如图,P为AB的黄金分割点(AP>PB),如果AP的长度为8,那么AB的长度是( )
A.4﹣4 B.12﹣4 C.12+4 D.4+4
5.一次函数y1=k1x+b和反比例函数y2=(k1 k2≠0)的图象如图所示,若y1>y2,则x的取值范围是( )
A.﹣2<x<0或x>1 B.﹣2<x<1
C.x<﹣2或x>1 D.x<﹣2或0<x<1
6.二次函数y=a(x﹣2)2+c与一次函数y=cx+a在同一坐标系中的大致图象是( )
A. B.
C. D.
7.在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给出以下结论:abc<0;c+2a<0;9a﹣3b+c=0;a﹣b≥m(am+b)(m为实数),其中错误结论的个数有( )
A.1个 B.2个 C.3个 D.4个
8.如图l1∥l2∥l3,直线AC与DF交于点O,且与l1,l2,l3分别交于点A,B,C,D,E,F,则下列比例式不正确的是( )
A.= B.= C.= D.=
9.如图,在平面直角坐标系中,点P在函数y=(x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣(x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )
A.逐渐变大 B.逐渐变小 C.等于定值16 D.等于定值24
10.如图,矩形ABCD中,AD=3,AB=2,点E为AB的中点,点F在边BC上,且BF=2FC,AF分别与DE、BD相交于点M、N,则MN的长为( )
A. B. C. D.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.在比例尺为1:500000的地图上,量得A、B两地的距离为3cm,则A、B两地的实际距离为 km.
12.已知线段a=2,b=8,则a,b的比例中项是 .
13.小红对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系为y=﹣,由此可知小红此次实心球训练的成绩为 米.
14.已知:=k,则k= .
三、(本大题共2小题,每小题8分,满分16分)
15.已知a、b、c是△ABC的三边,且满足==,a+b+c=12,试判断△ABC的形状,并说明理由.
16.已知抛物线y=﹣x2+bx+c过点(0,﹣3)和(2,1).
(1)试确定抛物线的解析式;
(2)求出抛物线与x轴的交点坐标和顶点坐标;
(3)画出函数图象、写出当y>0的x的取值范围.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,E是平行四边形ABCD的边BA延长线上一点,连接EC,交AD于F.
(1)写出图中的三对相似三角形(注意:不添加辅助线);
(2)请在你所找出的相似三角形中选一对,说明相似的理由.
18.如图:一次函数y=ax+b的图象与反比例函数y=的图象交于A(2,m)、B(﹣1,﹣4)两点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象直接写出,当x为何值时,ax+b﹣>0.
五、(本大题共2小题,每小题10分,满分20分)
19.为了预防流感,某学校用药熏消毒法对教室进行消毒.已知一瓶药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
(1)写出倾倒一瓶药物后,从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量不低于8毫克时,消毒有效,那么倾倒一瓶药物后,从药物释放开始,有效消毒时间是多少分钟?
20.如图,抛物线y=x2﹣bx+3与x轴相交于点A,B,且过点C(4,3).
(1)求b的值和该抛物线顶点P的坐标;
(2)将该抛物线向左平移,记平移后抛物线的顶点为P′,当四边形AP′PB为平行四边形时,求平移后抛物线的解析式.
六、(本题满分12分)
21.如图,在Rt△ABC中,∠A=90°,AB=8,AC=6.若动点D从点B出发,沿线段BA运动到点A为止,运动速度为每秒2个单位长度.过点D作DE∥BC交AC于点E,设动点D运动的时间为x秒,AE的长为y.
(1)求出y关于x的函数关系式,并写出自变量x的取值范围;
(2)求出△BDE的面积S与x之间的函数关系式;
(3)当x为何值时,△BDE的面积S有最大值,最大值为多少?
七、(本题满分12分)
22.某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额﹣生产费用)
(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,求今年可获得最大毛利润
八、(本题满分14分)
23.直线y=x﹣2与x、y轴分别交于点A、C.抛物线的图象经过A、C和点B(1,0).
(1)求抛物线的解析式和顶点G的坐标;
(2)在直线y=﹣1上是否存在点P,使得△PBG的周长最小?若存在,求出P点的坐标;若不存在,请说明理由.
(3)在直线AC上方的抛物线上有一动点D,当D与直线AC的距离DE最大时,求出点D的坐标,并求出最大距离是多少?
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)
1.已知y=(m+2)x|m|+2是关于x的二次函数,那么m的值为( )
A.﹣2 B.2 C.±2 D.0
【分析】根据形如y=ax2+bx+c (a≠0)是二次函数,可得答案.
解:∵y=(m+2)x|m|+2是y关于x的二次函数,
∴|m|=2且m+2≠0.
解得m=2.
故选:B.
2.抛物线y=﹣3(x+1)2﹣2经过平移得到抛物线y=﹣3x2,平移方法是( )
A.向左平移1个单位,再向下平移2个单位
B.向左平移1个单位,再向上平移2个单位
C.向右平移1个单位,再向下平移2个单位
D.向右平移1个单位,再向上平移2个单位
【分析】由抛物线y=﹣3(x+1)2﹣2得到顶点坐标为(﹣1,﹣2),而平移后抛物线y=﹣3x2的顶点坐标为(0,0),根据顶点坐标的变化寻找平移方法.
解:∵抛物线y=﹣3(x+1)2﹣2的顶点坐标为(﹣1,﹣2),
平移后抛物线y=﹣3x2的顶点坐标为(0,0),
∴平移方法为:向右平移1个单位,再向上平移2个单位.
故选:D.
3.二次函数y=ax2+bx的图象如图所示,若一元二次方程ax2+bx+m=0有实数根,则m的最大值为( )
A.3 B.﹣3 C. D.﹣
【分析】根据函数图象中的数据,可以得到该函数的最小值,再根据一元二次方程ax2+bx+m=0有实数根,从而可以求得m的取值范围,从而可以得到m的最大值.
解:由图象可得,
二次函数y=ax2+bx的最小值是y=﹣3,
∵一元二次方程ax2+bx+m=0有实数根,
即一元二次方程ax2+bx=﹣m有实数根,
也就是y=ax2+bx与y=﹣m有交点,
∴﹣m≥﹣3,
解得:m≤3,
∴m的最大值是3,
故选:A.
4.大自然巧夺天工,一片小枫树叶,也蕴含着“黄金分割”.如图,P为AB的黄金分割点(AP>PB),如果AP的长度为8,那么AB的长度是( )
A.4﹣4 B.12﹣4 C.12+4 D.4+4
【分析】根据黄金分割的定义得到AP=AB,然后把AP的长度代入可求出AB的长.
解:∵P为AB的黄金分割点(AP>PB),
∴AP=AB,
∴AB=AP=×8=4+4,
故选:D.
5.一次函数y1=k1x+b和反比例函数y2=(k1 k2≠0)的图象如图所示,若y1>y2,则x的取值范围是( )
A.﹣2<x<0或x>1 B.﹣2<x<1
C.x<﹣2或x>1 D.x<﹣2或0<x<1
【分析】直接利用两函数图象的交点横坐标得出y1>y2时,x的取值范围.
解:如图所示:
若y1>y2,则x的取值范围是:x<﹣2或0<x<1.
故选:D.
6.二次函数y=a(x﹣2)2+c与一次函数y=cx+a在同一坐标系中的大致图象是( )
A. B.
C. D.
【分析】可先根据一次函数的图象判断a、b的符号,再判断二次函数图象与实际是否相符,判断正误.
解:A、一次函数y=cx+a的图象与y轴交于负半轴,a<0,与二次函数y=a(x﹣2)2+c的图象开口向上,即a>0相矛盾,故A错误;
B、一次函数y=cx+a的图象过一、二、四象限,a>0,c<0,二次函数y=a(x﹣2)2+c的图象开口向上,顶点为(2,c)在第四象限,a>0,c<0,故B正确;
C、二次函数y=a(x﹣2)2+c的对称轴x=2,在y轴右侧,故C错误;
D、一次函数y=cx+a的图象过一、二、三象限,c>0,与抛物线y=a(x﹣2)2+c的顶点(2,c)在第四象限,c<0相矛盾,故D错误;
故选:B.
7.在平面直角坐标系中,二次函数y=ax2+bx+c(a≠0)的图象如图所示,现给出以下结论:abc<0;c+2a<0;9a﹣3b+c=0;a﹣b≥m(am+b)(m为实数),其中错误结论的个数有( )
A.1个 B.2个 C.3个 D.4个
【分析】由抛物线的开口方向判断a与0的关系,由抛物线与y轴的交点判断c与0的关系,然后根据对称轴及抛物线与x轴交点情况进行推理,进而对所得结论进行判断.
解:由抛物线可知:a>0,c<0,
对称轴x=﹣<0,
∴b>0,
∴abc<0;
由对称轴可知:﹣=﹣1,
∴b=2a,
∵x=1时,y=a+b+c=0,
∴c+3a=0,
∴c+2a=﹣3a+2a=﹣a<0;
(1,0)关于x=﹣1的对称点为(﹣3,0),
∴x=﹣3时,y=9a﹣3b+c=0;
当x=﹣1时,y的最小值为a﹣b+c,
∴x=m时,y=am2+bm+c,
∴am2+bm+c≥a﹣b+c,
即a﹣b≤m(am+b);
∴错误的为a﹣b≥m(am+b),有1个.
故选:A.
8.如图l1∥l2∥l3,直线AC与DF交于点O,且与l1,l2,l3分别交于点A,B,C,D,E,F,则下列比例式不正确的是( )
A.= B.= C.= D.=
【分析】平行线分线段成比例定理的内容是:一组平行线截两条直线,所截的线段对应成比例,根据以上内容判断即可.
解:A、∵l1∥l2∥l3,
∴=,故本选项错误;
B、∵l1∥l2∥l3,
∴=,故本选项错误;
C、∵l1∥l2∥l3,
∴=,故本选项错误;
D、∵l1∥l2∥l3,
∴=,故本选项正确;
故选:D.
9.如图,在平面直角坐标系中,点P在函数y=(x>0)的图象上从左向右运动,PA∥y轴,交函数y=﹣(x>0)的图象于点A,AB∥x轴交PO的延长线于点B,则△PAB的面积( )
A.逐渐变大 B.逐渐变小 C.等于定值16 D.等于定值24
【分析】根据反比例函数k的几何意义得出S△POC=×2=1,S矩形ACOD=6,即可得出=,从而得出=,通过证得
△POC∽△PBA,得出=()2=,即可得出S△PAB=16S△POC=16.
解:由题意可知S△POC=×2=1,S矩形ACOD=6,
∵S△POC=OC PC,S矩形ACOD=OC AC,
∴==,
∴=,
∴=,
∵AB∥x轴,
∴△POC∽△PBA,
∴=()2=,
∴S△PAB=16S△POC=16,
∴△PAB的面积等于定值16.
故选:C.
10.如图,矩形ABCD中,AD=3,AB=2,点E为AB的中点,点F在边BC上,且BF=2FC,AF分别与DE、BD相交于点M、N,则MN的长为( )
A. B. C. D.
【分析】过点F作FH⊥AD于H,交ED于O,得FH=AB=2,由勾股定理得AF=2,根据平行线分线段成比例得OH=,由相似三角形的性质得,求得AM,再根据相似三角形的性质求得AN=,即可得出结果.
解:如图,过点F作FH⊥AD于H,交ED于O,
则FH=AB=2,
∵BF=2FC,
∴BF=AH=2,FC=HD=1,
∴AF==2,
∵OH∥AE,
∴,
∴OF=FH﹣OH=2﹣=,
∵AE∥FO,
∴△AME∽△FMO,
∴,
∴AM=,
∵AD∥BF,
∴△AND∽△FNB,
∴,
∴AN=,
∴MN=AN﹣AM==,
故选:B.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.在比例尺为1:500000的地图上,量得A、B两地的距离为3cm,则A、B两地的实际距离为 15 km.
【分析】由在比例尺为1:50000的地图上,量得A、B两地的图上距离AB=3cm,根据比例尺的定义,可求得两地的实际距离.
解:∵比例尺为1:500000,量得两地的距离是3厘米,
∴A、B两地的实际距离3×500000=1500000cm=15km,
故答案为15.
12.已知线段a=2,b=8,则a,b的比例中项是 4 .
【分析】设线段a,b的比例中项为c,根据比例中项的定义可知,c2=ab,代入数据可直接求得c的值,注意两条线段的比例中项为正数.
解:设线段a,b的比例中项为c,
∵c是长度分别为2、8的两条线段的比例中项,
∴c2=ab=2×8,
即c2=16,
∴c=4(负数舍去).
故答案为:4.
13.小红对自己某次实心球训练的录像进行分析,发现实心球飞行高度y(米)与水平距离x(米)之间的关系为y=﹣,由此可知小红此次实心球训练的成绩为 10 米.
【分析】根据铅球落地时,高度y=0,把实际问题可理解为当y=0时,求x的值即可.
解:当y=0时,y=﹣x2+x+=0,
解得:x1=﹣2(舍去),x2=10,
∴小红此次实心球训练的成绩为10米.
故答案为:10.
14.已知:=k,则k= 2或﹣1 .
【分析】能够根据比例的基本性质熟练进行比例式和等积式的互相转换.
解:此题要分情况考虑:
当x+y+z≠0时,则根据比例的等比性质,得k==2;
当x+y+z=0时,即x+y=﹣z,则k=﹣1,故填2或﹣1.
三、(本大题共2小题,每小题8分,满分16分)
15.已知a、b、c是△ABC的三边,且满足==,a+b+c=12,试判断△ABC的形状,并说明理由.
【分析】设===k,表示a、b、c的长,代入a+b+c=12中,计算k的值,可得三边的长,根据勾股定理的逆定理可得结论.
解:△ABC是直角三角形,理由是:
设===k,
则a=3k﹣4,b=2k﹣3,c=4k﹣8,
∵a+b+c=12,
∴3k﹣4+2k﹣3+4k﹣8=12,
∴k=3,
∴a=5,b=3,c=4,
∴b2+c2=32+42=25=a2,
∴△ABC是直角三角形.
16.已知抛物线y=﹣x2+bx+c过点(0,﹣3)和(2,1).
(1)试确定抛物线的解析式;
(2)求出抛物线与x轴的交点坐标和顶点坐标;
(3)画出函数图象、写出当y>0的x的取值范围.
【分析】(1)把(0,﹣3)和(2,1)代入抛物线,得出方程组,求出方程组的解,即可得出抛物线的解析式;
(2)把y=0代入解析式,求出x的值,即可得出抛物线与x轴的交点坐标,把抛物线解析式改写成顶点式即可;
(3)根据函数解析式,列表,描点,画图,根据图象即可求出当y>0时x的取值范围.
解:(1)∵抛物线y=﹣x2+bx+c过点(0,﹣3)和(2,1),
∴,
解得 ,
抛物线的解析式为y=﹣x2+4x﹣3;
(2)令y=0,得﹣x2+4x﹣3=0,即 x2﹣4x+3=0,
∴x1=1,x2=3,
∴抛物线与x轴的交点坐标为(1,0)、(3,0),
∵抛物线的解析式为y=﹣x2+4x﹣3=﹣(x﹣2)2+1,
∴顶点坐标为:(2,1);
(3)列表:
画图:
由图象可知,当y>0时,1<x<3.
四、(本大题共2小题,每小题8分,满分16分)
17.如图,E是平行四边形ABCD的边BA延长线上一点,连接EC,交AD于F.
(1)写出图中的三对相似三角形(注意:不添加辅助线);
(2)请在你所找出的相似三角形中选一对,说明相似的理由.
【分析】(1)证明△EAF∽△EBC,△CDF∽△EBC,△CDF∽△EAF即可;
(2)根据平行线定理可求得∠EAF=∠B,进而可以求证△EAF∽△EBC即可解题.
解:(1)△EAF∽△EBC,△CDF∽△EBC,△CDF∽△EAF.
(2)选△EAF∽△EBC,
理由如下:在ABCD中AD∥BC,
∴∠EAF=∠B.
又∵∠E=∠E,
∴△EAF∽△EBC.
18.如图:一次函数y=ax+b的图象与反比例函数y=的图象交于A(2,m)、B(﹣1,﹣4)两点.
(1)求反比例函数和一次函数的解析式;
(2)求△AOB的面积;
(3)根据图象直接写出,当x为何值时,ax+b﹣>0.
【分析】(1)把点B坐标代入反比例函数求解析式,然后求出点A坐标,再将A,B坐标代入一次函数解析式求解.
(2)设直线AB与y轴交于点C,由S△AOB=S△BOC+S△AOC求解.
(3)由ax+b﹣>0得ax+b>,再根据图象交点横坐标求解.
解:(1)把(﹣1,﹣4)代入y=中得﹣4=,
解得k=4,
∴反比例函数解析式为y=,
把(2,m)代入y=中得m==2,
∴点A坐标为(2,2)
把(﹣1,﹣4),(2,2)代入y=ax+b得,
解得,
∴一次函数解析式为y=2x﹣2.
(2)设直线AB与y轴交于点C,
把x=0代入y=2x﹣2得y=﹣2,
∴OC=2.
∴S△AOB=S△BOC+S△AOC=×OC |xB|+×OC xA=×2×1+2×2=3.
(3)由ax+b﹣>0得ax+b>,
∵直线与双曲线交点为A(2,2)、B(﹣1,﹣4),
∴﹣1<x<0或x>2时ax+b>.
五、(本大题共2小题,每小题10分,满分20分)
19.为了预防流感,某学校用药熏消毒法对教室进行消毒.已知一瓶药物释放过程中,室内每立方米空气中的含药量y(毫克)与时间x(分钟)成正比例;药物释放完毕后,y与x成反比例,如图所示.根据图中提供的信息,解答下列问题:
(1)写出倾倒一瓶药物后,从药物释放开始,y与x之间的两个函数关系式及相应的自变量取值范围;
(2)据测定,当空气中每立方米的含药量不低于8毫克时,消毒有效,那么倾倒一瓶药物后,从药物释放开始,有效消毒时间是多少分钟?
【分析】(1)根据函数图象找出点的坐标,再根据点的坐标利用待定系数法即可求出一次函数和反比例函数的关系式;
(2)将y=8分别代入两函数关系式中求出x值,二者做差即可得出结论.
解:(1)当0≤x≤15时,设y=ax(a≠0);当x≥15时,设y=(k≠0).
将(15,20)代入y=ax,
20=15a,解得:a=,
∴y=x(0≤x≤15).
将(15,20)代入y=,
20=,解得:k=300,
∴y=(x≥15).
(2)当y=x=8时,x=6;
当y==8时,x=37.5.
37.5﹣6=31.5(分钟).
答:有效消毒时间是31.5分钟.
20.如图,抛物线y=x2﹣bx+3与x轴相交于点A,B,且过点C(4,3).
(1)求b的值和该抛物线顶点P的坐标;
(2)将该抛物线向左平移,记平移后抛物线的顶点为P′,当四边形AP′PB为平行四边形时,求平移后抛物线的解析式.
【分析】(1)根据抛物线y=x2﹣bx+3过点C(4,3),代入求出b的值即可,再利用配方法求出顶点坐标即可;
(2)首先求出AB的长,再根据四边形AP′PB为平行四边形,得出P′P=AB=2,进而得出P′的坐标,求出解析式即可.
解:(1)当x=4,y=3,代入y=x2﹣bx+3,
解得:b=4,
∴y=x2﹣4x+3=(x﹣2)2﹣1,
∴b的值为4,和该抛物线顶点P的坐标为:(2,﹣1);
(2)当y=0时,x2﹣4x+3=0,
解得:x1=1,x2=3,
∴AB=2,
∵四边形AP′PB为平行四边形,
∴P′P=AB=2,
∴P′的坐标是(0,﹣1),
∴抛物线的解析式是:y=x2﹣1.
六、(本题满分12分)
21.如图,在Rt△ABC中,∠A=90°,AB=8,AC=6.若动点D从点B出发,沿线段BA运动到点A为止,运动速度为每秒2个单位长度.过点D作DE∥BC交AC于点E,设动点D运动的时间为x秒,AE的长为y.
(1)求出y关于x的函数关系式,并写出自变量x的取值范围;
(2)求出△BDE的面积S与x之间的函数关系式;
(3)当x为何值时,△BDE的面积S有最大值,最大值为多少?
【分析】(1)由平行线得△ABC∽△ADE,根据相似形的性质得关系式;
(2)s= BD AE;
(3)运用函数性质求解.
解:(1)∵DE∥BC,
∴△ADE∽△ABC.
∴.
又∵AD=8﹣2x,AB=8,AE=y,AC=6,
∴.
∴.
自变量x的取值范围为0≤x≤4.
(2)S=BD AE= 2x y
=﹣x2+6x
(3)S=﹣x2+6x
=﹣x2+6x+9﹣9
=﹣(x﹣2)2+6.
∴当x=2时,S有最大值,且最大值为6.
七、(本题满分12分)
22.某市在党中央实施“精准扶贫”政策的号召下,大力开展科技扶贫工作,帮助农民组建农副产品销售公司,某农副产品的年产量不超过100万件,该产品的生产费用y(万元)与年产量x(万件)之间的函数图象是顶点为原点的抛物线的一部分(如图①所示);该产品的销售单价z(元/件)与年销售量x(万件)之间的函数图象是如图②所示的一条线段,生产出的产品都能在当年销售完,达到产销平衡,所获毛利润为w万元.(毛利润=销售额﹣生产费用)
(1)请直接写出y与x以及z与x之间的函数关系式;
(2)求w与x之间的函数关系式;
(3)由于受资金的影响,今年投入生产的费用不会超过360万元,求今年可获得最大毛利润
【分析】(1)利用待定系数法可求出y与x以及z与x之间的函数关系式;
(2)根据(1)的表达式及毛利润=销售额﹣生产费用,可得出w与x之间的函数关系式;
(3)首先求出x的取值范围,再利用二次函数增减性得出答案即可.
解:(1)图①可得函数经过点(100,1000),
设抛物线的解析式为y=ax2(a≠0),
将点(100,1000)代入得:1000=10000a,
解得:a=,
故y与x之间的关系式为y=x2,
图②可得:函数经过点(0,30)、(100,20),
设z=kx+b,则,
解得:,
故z与x之间的关系式为z=﹣x+30;
(2)w=zx﹣y
=﹣x2+30x﹣x2
=﹣x2+30x,
∴w与x之间的函数关系式为w=﹣x2+30x;
(3)令y=360,得x2=360,
解得:x=±60(负值舍去),
由图象可知,当0<y≤360时,0<x≤60,
w=﹣x2+30x
=﹣(x2﹣150x)
=﹣(x﹣75)2+1125,
∵﹣<0,
∴当x≤75时,w随x的增大而增大,
∵0<x≤60,
∴当x=60时,w有最大值,最大值为﹣(60﹣75)2+1125=1080,
答:今年最多可获得毛利润1080万元.
八、(本题满分14分)
23.直线y=x﹣2与x、y轴分别交于点A、C.抛物线的图象经过A、C和点B(1,0).
(1)求抛物线的解析式和顶点G的坐标;
(2)在直线y=﹣1上是否存在点P,使得△PBG的周长最小?若存在,求出P点的坐标;若不存在,请说明理由.
(3)在直线AC上方的抛物线上有一动点D,当D与直线AC的距离DE最大时,求出点D的坐标,并求出最大距离是多少?
【分析】(1)用待定系数法即可求解;
(2)作点B关于直线y=﹣1的对称点H(1,﹣2),连接GH交直线y=﹣1于点P,在点P为所求点,进而求解;
(3)由S△ACD=S梯形AGFC﹣S△CDF﹣S△ADG=(AG+FC) FG﹣FC FD﹣DG AG,即可求解.
解:(1)在直线解析式y=x﹣2中,令x=0,得y=﹣2;令y=0,得x=4,
∴A(4,0),C(0,﹣2).
设抛物线的解析式为y=ax2+bx+c,
∵点A(4,0),B(1,0),C(0,﹣2)在抛物线上,
则,解得,
∴抛物线的解析式为:y=﹣x2+x﹣2;
抛物线的对称轴为x=,当x=时,y=﹣x2+x﹣2=,故点G(,);
(2)在直线y=﹣1上存在点P,使得使得△PBG的周长最小,
作点B关于直线y=﹣1的对称点H(1,﹣2),连接GH交直线y=﹣1于点P,在点P为所求点,
理由:△PBG的周长=BG+BP+PG=BG+PH+PG=GH+GB为最小,
由点BG的坐标得,直线BG的表达式为y=x﹣,
当y=1=x﹣,解得x=,
故点P的坐标为(,﹣1);
(3)设点D坐标为(x,y),则y=﹣x2+x﹣2,
在Rt△AOC中,OA=4,OC=2,由勾股定理得:AC=2.
连接CD、AD,过点D作DF⊥y轴于点F,过点A作AG⊥FD交FD的延长线于点G,
则FD=x,DG=4﹣x,OF=AG=y,FC=y+2.
S△ACD=S梯形AGFC﹣S△CDF﹣S△ADG=(AG+FC) FG﹣FC FD﹣DG AG=(y+y+2)×4﹣(y+2) x﹣(4﹣x) y=2y﹣x+4,
将y=﹣x2+x﹣2代入得:S△ACD=2y﹣x+4=﹣x2+4x=﹣(x﹣2)2+4,
∴当x=2时,△ACD的面积最大,最大值为4.
当x=2时,y=1,∴D(2,1).
∵S△ACD=AC DE,AC=2,
∴当△ACD的面积最大时,高DE最大,
则DE的最大值为:.
∴当D与直线AC的距离DE最大时,点D的坐标为(2,1),最大距离为.
同课章节目录
