2021-2022学年高一上学期数学人教A版(2019)必修第一册5.1.1任意角课件(共23张PPT)
文档属性
| 名称 | 2021-2022学年高一上学期数学人教A版(2019)必修第一册5.1.1任意角课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 13:57:10 | ||
图片预览




文档简介
(共23张PPT)
必修第一册
5.1.1 任意角
深圳
SEOUL
SYDNEY
请问飞机从SYDNEY飞抵深圳后,乘客应如何校准手表 若再由深圳飞往SEOUL,又应如何校准手表
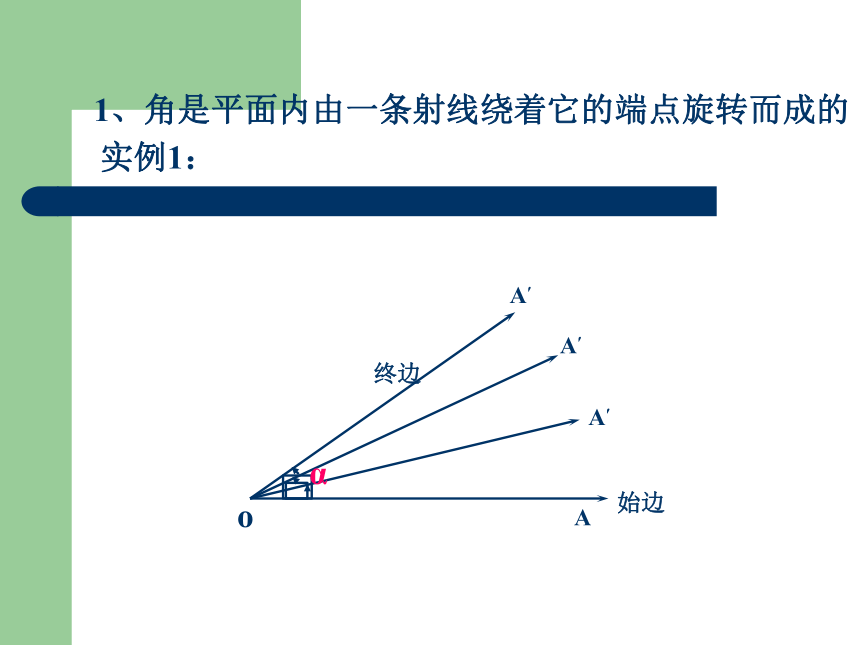
o
A
A′
A′
始边
A′
α
终边
1、角是平面内由一条射线绕着它的端点旋转而成的
实例1:
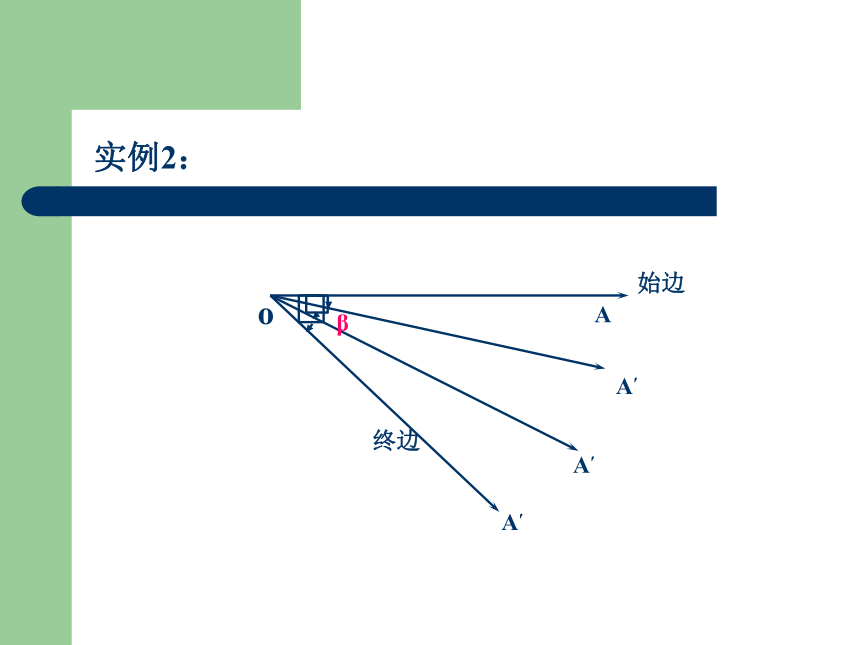
o
A
A′
A′
始边
β
A′
终边
实例2:
A
A′
A′
A′
A′
A′
A′
A′
A′
A′
A′
α′
实例3:
A′
A′
A′
A′
A′
A′
A′
A′
A′
α′
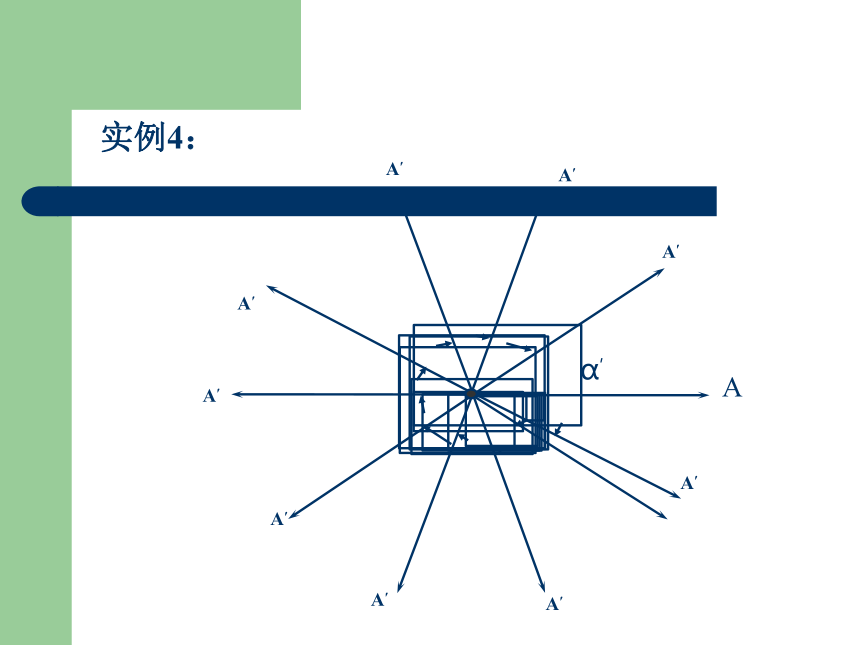
实例4:
A
按逆时针方向旋转所形成的角叫做正角;
按顺时针方向旋转所形成的角叫做负角;
如果射线没有作任何旋转,那么也把它看成一个角,叫做零角.
把角的概念推广到任意角
x
y
o
始边
终边
终边
终边
终边
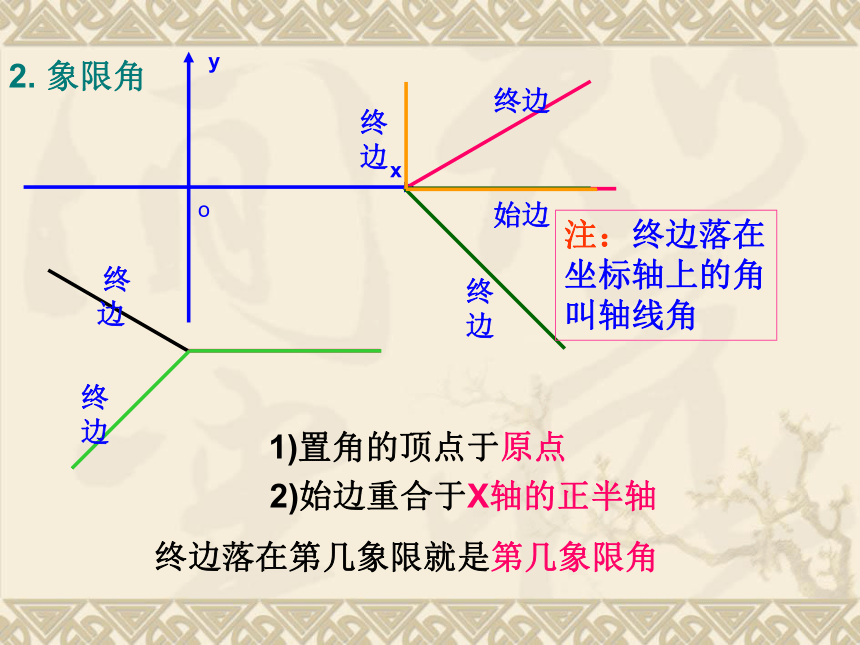
1)置角的顶点于原点
终边落在第几象限就是第几象限角
2)始边重合于X轴的正半轴
终边
注:终边落在坐标轴上的角叫轴线角
2. 象限角
x
y
o
300
3900
-3300
3900=3600+300
-3300=-3600+300
=1x3600+300
=-1x3600+ 300
300= =0x3600+300
2x3600+300 , -2x3600+ 300
3x3600+300 , -3x3600+ 300
… , … ,
与300终边相同的角的一般形
式为K·3600+ 300,K ∈ Z
与α终边相同的角的一般形式为
K·3600+α,K ∈ Z
S= { | =k·360°+ , k∈Z}
注意:⑴K ∈ Z ⑵α为任意角
⑶终边相同的角有无数个
3. 终边相同的角
例1 把下列各角写成K·3600 +α(00≤α<3600,k∈Z)的形式,并判定它们分别是第几象限角:
(1) 1990°12′; (2) -2010°;
解 : (1) 因为1990°12′=5×360°+190°12′
190°12′是与1990°12′终边相同的角
因为190°12′是第三象限的角,
所以1990°12′是第三象限的角
(2)因为-2010°
= (-6)×360°+150°
-2008°是与150°终边相同的角
所以-2010°是第二象限的角
判断角的象限方法
1.写成K·3600+α (00≤α<3600,
k∈Z)的形式
2.由α的象限得出结论
例2 写出终边落在各坐标半轴上的角的集合。
终边落在坐标轴上的情形
x
y
o
0°
90°
180°
270°
K·360°+
K·360°+
K·360°+
K·360°+
或K·360°+ 360°
例3 写出终边落在y轴上的角的集合。
解:终边落在y轴正半轴上的角的集合为
S1={β|β=K 360°+90°,K∈Z}
={β|β=2K 180°+90°,K∈Z}
={β|β=180°的偶数倍+90°}
终边落在y轴负半轴上的角的集合为
S2={β|β=K 360°+270°,K∈Z}
={β|β=2K 180°+180°+90°,K∈Z}
={β|β=(2K+1)180°+90° ,K∈Z}
={β|β=180°的奇数倍+90°}
S=S1∪S2
所以 终边落在y轴上的角的集合为
={β| β=180°的偶数倍+90°}
∪{β| β=180°的奇数倍+90°}
={β| β=180°+90° 的整数倍}
={β| β=K 180°+ 90° ,K∈Z}
{偶数}∪{奇数}
={整数}
X
Y
O
90°+K 360°
270°+k 360°
写出终边落在 轴上的角的集合。
解:终边落在 轴非负半轴上的角的集合为
S1={β|β=K 360°,K∈Z}
={β|β=2K 180°,K∈Z}
={β|β=180°的偶数倍}
终边落在 轴负半轴上的角的集合为
S2={β|β=K 360°+180°,K∈Z}
={β|β=2K 180°+180°,K∈Z}
={β|β=(2K+1)180° ,K∈Z}
={β|β=180°的奇数倍}
S=S1∪S2
所以 终边落在 x 轴上的角的集合为
={β| β=180° 的整数倍}
={β|β=K 180° ,K∈Z}
{偶数}∪{奇数}
={整数}
X
Y
O
K 360°
180°+k 360°
x
x
x
练习:
结论:
1.终边在x轴、y轴上的角的集合
终边在x轴上:
S={α|α=k·180°,k∈Z}.
终边在y轴上:
S={α|α=90°+k·180°,k∈Z}.
2.第一、二、三、四象限的角的集合
第一象限:
S={α|k·3600<α<900+k·3600,k∈Z};
第二象限:
S={α|900+k·3600<α<1800+k·3600,k∈Z};
第三象限:
S={α|1800+k·3600<α<2700+k·3600,k∈Z};
第四象限:
S={α|-900+k·3600<α例4.如果 是第三象限角,那么2 角终边的位置如
何 是哪个象限的角
解:
利用上述方法判断,可得如下结论:
x
y
o
1
2
3
4
1
2
3
4
练习 在0 o ~ 360 o之间,找出与下列各角终边相同的角,并判断各角所在的象限:
① -20 o ② 740 o ③ 950 o 48′
解:
①α=k·360 o -20 o
当k=1时, α =340 o
∴ -20 o与340 o终边相同都在第四象限。
②α=k·360 o+740 o
当k=-2时, α=20 o
∴ -20 o与740 o 终边相同都在第一象限。
③ α=k·360 o+950 o 48′
当k=-2时, α =230 o 48 ′
∴ -950 o 48′与230 o 48 ′ 终边相同都在第三象限
课本例3 写出终边在直线y=x上的角的集合s,并把s中适合不等式-360°≤ β<720°的元素β写出来.
小结:
1.任意角的概念
正角:射线按逆时针方向旋转形成的角
负角:射线按顺时针方向旋转形成的角
零角:射线不作旋转形成的角
1)置角的顶点于原点
2)始边重合于X轴的正半轴
2.象限角
3)终边落在第几象限就是第几象限角
3 . 终边与 角α相同的角
K·360°+α,K∈Z
4.轴线角:
5.区间角:
终边落在X轴正上的角
终边落在X轴负上的角
终边落在Y轴正上的角
终边落在Y轴负上的角
终边落在X轴上的角
终边落在X轴上的角
如(00,900)
作业
P9 A组1.2.3.4
必修第一册
5.1.1 任意角
深圳
SEOUL
SYDNEY
请问飞机从SYDNEY飞抵深圳后,乘客应如何校准手表 若再由深圳飞往SEOUL,又应如何校准手表
o
A
A′
A′
始边
A′
α
终边
1、角是平面内由一条射线绕着它的端点旋转而成的
实例1:
o
A
A′
A′
始边
β
A′
终边
实例2:
A
A′
A′
A′
A′
A′
A′
A′
A′
A′
A′
α′
实例3:
A′
A′
A′
A′
A′
A′
A′
A′
A′
α′
实例4:
A
按逆时针方向旋转所形成的角叫做正角;
按顺时针方向旋转所形成的角叫做负角;
如果射线没有作任何旋转,那么也把它看成一个角,叫做零角.
把角的概念推广到任意角
x
y
o
始边
终边
终边
终边
终边
1)置角的顶点于原点
终边落在第几象限就是第几象限角
2)始边重合于X轴的正半轴
终边
注:终边落在坐标轴上的角叫轴线角
2. 象限角
x
y
o
300
3900
-3300
3900=3600+300
-3300=-3600+300
=1x3600+300
=-1x3600+ 300
300= =0x3600+300
2x3600+300 , -2x3600+ 300
3x3600+300 , -3x3600+ 300
… , … ,
与300终边相同的角的一般形
式为K·3600+ 300,K ∈ Z
与α终边相同的角的一般形式为
K·3600+α,K ∈ Z
S= { | =k·360°+ , k∈Z}
注意:⑴K ∈ Z ⑵α为任意角
⑶终边相同的角有无数个
3. 终边相同的角
例1 把下列各角写成K·3600 +α(00≤α<3600,k∈Z)的形式,并判定它们分别是第几象限角:
(1) 1990°12′; (2) -2010°;
解 : (1) 因为1990°12′=5×360°+190°12′
190°12′是与1990°12′终边相同的角
因为190°12′是第三象限的角,
所以1990°12′是第三象限的角
(2)因为-2010°
= (-6)×360°+150°
-2008°是与150°终边相同的角
所以-2010°是第二象限的角
判断角的象限方法
1.写成K·3600+α (00≤α<3600,
k∈Z)的形式
2.由α的象限得出结论
例2 写出终边落在各坐标半轴上的角的集合。
终边落在坐标轴上的情形
x
y
o
0°
90°
180°
270°
K·360°+
K·360°+
K·360°+
K·360°+
或K·360°+ 360°
例3 写出终边落在y轴上的角的集合。
解:终边落在y轴正半轴上的角的集合为
S1={β|β=K 360°+90°,K∈Z}
={β|β=2K 180°+90°,K∈Z}
={β|β=180°的偶数倍+90°}
终边落在y轴负半轴上的角的集合为
S2={β|β=K 360°+270°,K∈Z}
={β|β=2K 180°+180°+90°,K∈Z}
={β|β=(2K+1)180°+90° ,K∈Z}
={β|β=180°的奇数倍+90°}
S=S1∪S2
所以 终边落在y轴上的角的集合为
={β| β=180°的偶数倍+90°}
∪{β| β=180°的奇数倍+90°}
={β| β=180°+90° 的整数倍}
={β| β=K 180°+ 90° ,K∈Z}
{偶数}∪{奇数}
={整数}
X
Y
O
90°+K 360°
270°+k 360°
写出终边落在 轴上的角的集合。
解:终边落在 轴非负半轴上的角的集合为
S1={β|β=K 360°,K∈Z}
={β|β=2K 180°,K∈Z}
={β|β=180°的偶数倍}
终边落在 轴负半轴上的角的集合为
S2={β|β=K 360°+180°,K∈Z}
={β|β=2K 180°+180°,K∈Z}
={β|β=(2K+1)180° ,K∈Z}
={β|β=180°的奇数倍}
S=S1∪S2
所以 终边落在 x 轴上的角的集合为
={β| β=180° 的整数倍}
={β|β=K 180° ,K∈Z}
{偶数}∪{奇数}
={整数}
X
Y
O
K 360°
180°+k 360°
x
x
x
练习:
结论:
1.终边在x轴、y轴上的角的集合
终边在x轴上:
S={α|α=k·180°,k∈Z}.
终边在y轴上:
S={α|α=90°+k·180°,k∈Z}.
2.第一、二、三、四象限的角的集合
第一象限:
S={α|k·3600<α<900+k·3600,k∈Z};
第二象限:
S={α|900+k·3600<α<1800+k·3600,k∈Z};
第三象限:
S={α|1800+k·3600<α<2700+k·3600,k∈Z};
第四象限:
S={α|-900+k·3600<α
何 是哪个象限的角
解:
利用上述方法判断,可得如下结论:
x
y
o
1
2
3
4
1
2
3
4
练习 在0 o ~ 360 o之间,找出与下列各角终边相同的角,并判断各角所在的象限:
① -20 o ② 740 o ③ 950 o 48′
解:
①α=k·360 o -20 o
当k=1时, α =340 o
∴ -20 o与340 o终边相同都在第四象限。
②α=k·360 o+740 o
当k=-2时, α=20 o
∴ -20 o与740 o 终边相同都在第一象限。
③ α=k·360 o+950 o 48′
当k=-2时, α =230 o 48 ′
∴ -950 o 48′与230 o 48 ′ 终边相同都在第三象限
课本例3 写出终边在直线y=x上的角的集合s,并把s中适合不等式-360°≤ β<720°的元素β写出来.
小结:
1.任意角的概念
正角:射线按逆时针方向旋转形成的角
负角:射线按顺时针方向旋转形成的角
零角:射线不作旋转形成的角
1)置角的顶点于原点
2)始边重合于X轴的正半轴
2.象限角
3)终边落在第几象限就是第几象限角
3 . 终边与 角α相同的角
K·360°+α,K∈Z
4.轴线角:
5.区间角:
终边落在X轴正上的角
终边落在X轴负上的角
终边落在Y轴正上的角
终边落在Y轴负上的角
终边落在X轴上的角
终边落在X轴上的角
如(00,900)
作业
P9 A组1.2.3.4
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
