初中几何:特殊角或特殊值解题时的妙用(九年级上期末及中考一轮复习专用,含答案)
文档属性
| 名称 | 初中几何:特殊角或特殊值解题时的妙用(九年级上期末及中考一轮复习专用,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 10:19:19 | ||
图片预览


文档简介
中小学教育资源及组卷应用平台
初中几何:特殊角或特殊值在解题时的妙用
初中数学 九年级上期末 或中考一轮复习专用
在解几何题时,我们常常会碰到一些特殊角:30 、45 、60 ,还有一些特殊数值:
,,。
不过有时还可能出现以下两种情况:
①有时特殊角是15 ,那么我们可以适当变换:15 =45 -30 =60 -45 ,或者利用倍角30 =2×15 (通常要用到外角定理);
②有时题目中特殊角或特殊值没有明确给出,比较隐含,需要我们去挖掘。
碰到含有这些特殊值的题目时,应该怎么办?不用怕,其实,这种题目有很强的解题方法和技巧!
当看到这些特殊角/值时,一般情况下,我们不用多想:直接利用特殊角或特殊值所表示的角或线段,构造直角三角形或等边三角形。
1、30°/60 特殊角的应用
例1、如图,平行四边形ABCD的对角线AC,BD相交于点O,AB=5,BC=6.
(1)求OD长的取值范围;
(2)若∠CBD=30°,求OD的长.
解:(1)提示:∵CD=5,BC=6,1<BD<11,OD为BD的一半
∴
(2)过C作CE⊥BD于E,(因为∠CBD=30°为特殊角,那么我们直接过点C作CE⊥BD,构造两个直角三角形)
Rt△CBE中,∵∠CBD=30°,BC=6,
∴CE=3,BE==3,
在Rt△CED中,CD2=DE2+CE2,
代入CD、CE的值,解得:DE=4,
∴BD=BE+DE=3+4,
∴OD=BD=+2,
则OD的长是+2.
2、45°特殊角的应用
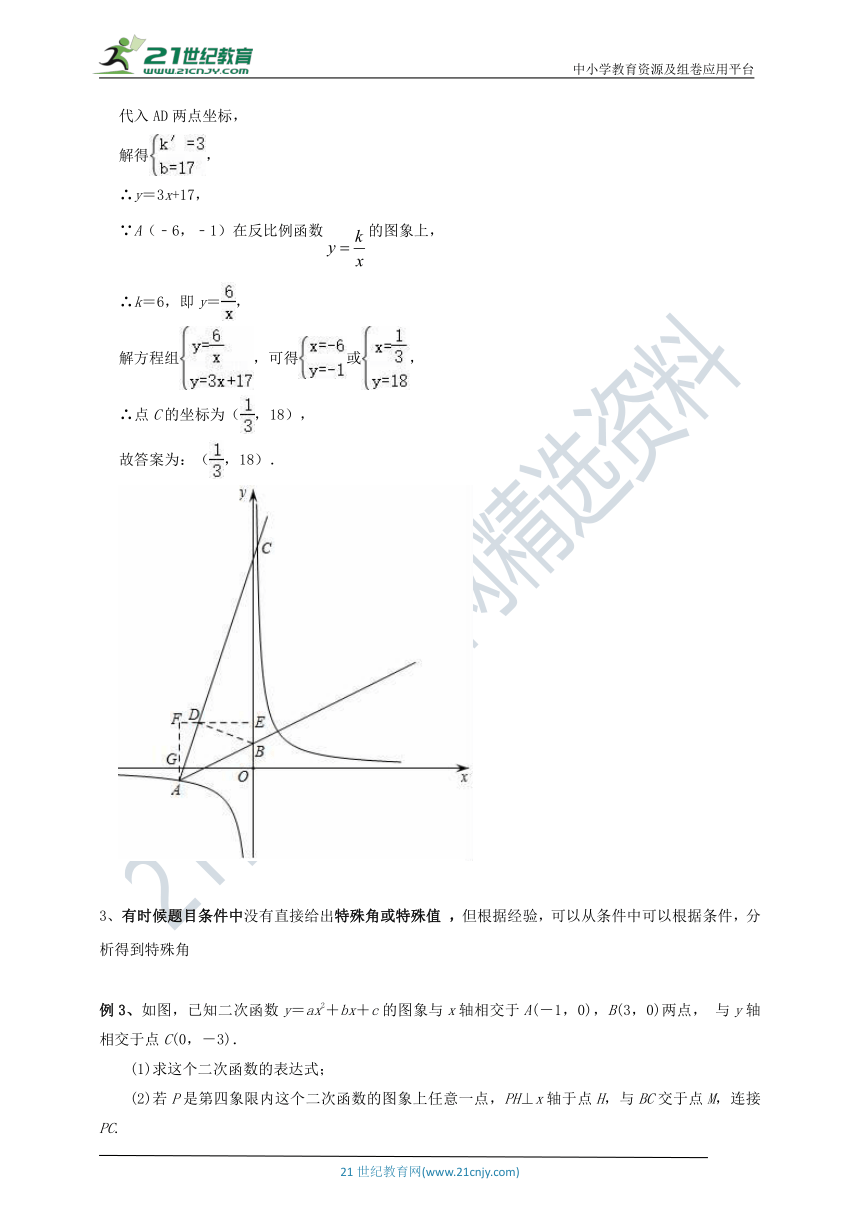
例2、如图,已知点B(0,2),A(﹣6,﹣1)在反比例函数的图象上,作射线AB,再将射线AB绕点A逆时针旋转45°后,交反比例函数图象于点C,则点C的坐标为 .
解:如图所示,过B作BD⊥AC于D,(因为∠CBD=30°为特殊角,那么我们直接过点C作CE⊥BD,构造两个直角三角形)
过D作DE⊥y轴于E,过A作AF⊥DE于F,则△ABD为等腰直角三角形,易得△AFD ≌△DEB,
设DF=BE=a,
∵B(0,2),A(﹣6,﹣1),
∴OE=a+2=GF,DE=6﹣a,AF=a+3,
∵AF=DE,
∴a+3=6﹣a,
解得a=,
∴D(,),
设直线AD的解析式为y=k'x+b,则
代入AD两点坐标,
解得,
∴y=3x+17,
∵A(﹣6,﹣1)在反比例函数的图象上,
∴k=6,即y=,
解方程组,可得或,
∴点C的坐标为(,18),
故答案为:(,18).
有时候题目条件中没有直接给出特殊角或特殊值 ,但根据经验,可以从条件中可以根据条件,分析得到特殊角
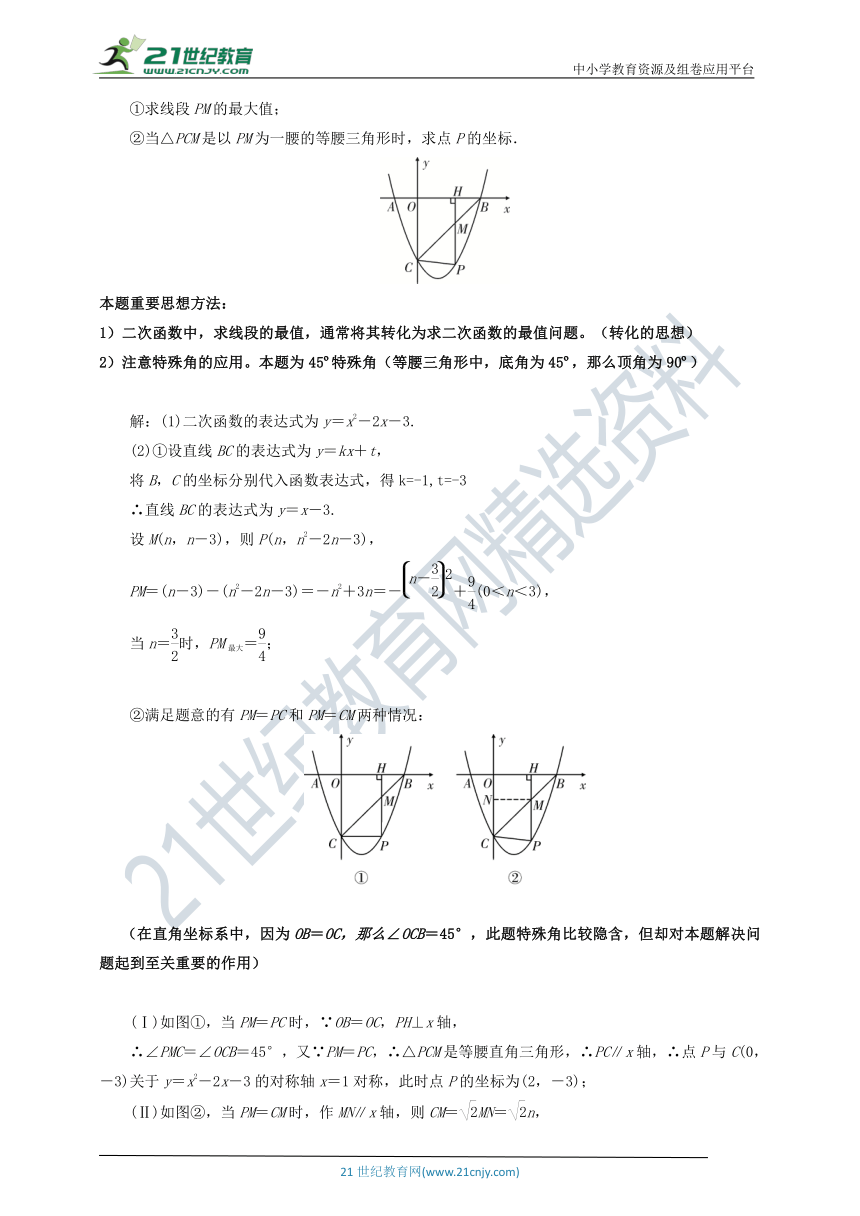
例3、如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(-1,0),B(3,0)两点, 与y轴相交于点C(0,-3).
(1)求这个二次函数的表达式;
(2)若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC.
①求线段PM的最大值;
②当△PCM是以PM为一腰的等腰三角形时,求点P的坐标.
本题重要思想方法:
1)二次函数中,求线段的最值,通常将其转化为求二次函数的最值问题。(转化的思想)
2)注意特殊角的应用。本题为45 特殊角(等腰三角形中,底角为45 ,那么顶角为90 )
解:(1)二次函数的表达式为y=x2-2x-3.
(2)①设直线BC的表达式为y=kx+t,
将B,C的坐标分别代入函数表达式,得k=-1,t=-3
∴直线BC的表达式为y=x-3.
设M(n,n-3),则P(n,n2-2n-3),
PM=(n-3)-(n2-2n-3)=-n2+3n=-+(0<n<3),
当n=时,PM最大=;
②满足题意的有PM=PC和PM=CM两种情况:
(在直角坐标系中,因为OB=OC,那么∠OCB=45°,此题特殊角比较隐含,但却对本题解决问题起到至关重要的作用)
(Ⅰ)如图①,当PM=PC时,∵OB=OC,PH⊥x轴,
∴∠PMC=∠OCB=45°,又∵PM=PC,∴△PCM是等腰直角三角形,∴PC∥x轴,∴点P与C(0,-3)关于y=x2-2x-3的对称轴x=1对称,此时点P的坐标为(2,-3);
(Ⅱ)如图②,当PM=CM时,作MN∥x轴,则CM=MN=n,
∴-n2+3n=n,∵n>0,∴n=3-,
又∵n2-2n-3=(n+1)(n-3)=2-4,
则此时P点坐标为(3-,2-4).
综上所述,点P的坐标为(2,-3)或(3-,2-4).
4、特殊值的应用(本题中特殊值为隐含条件)
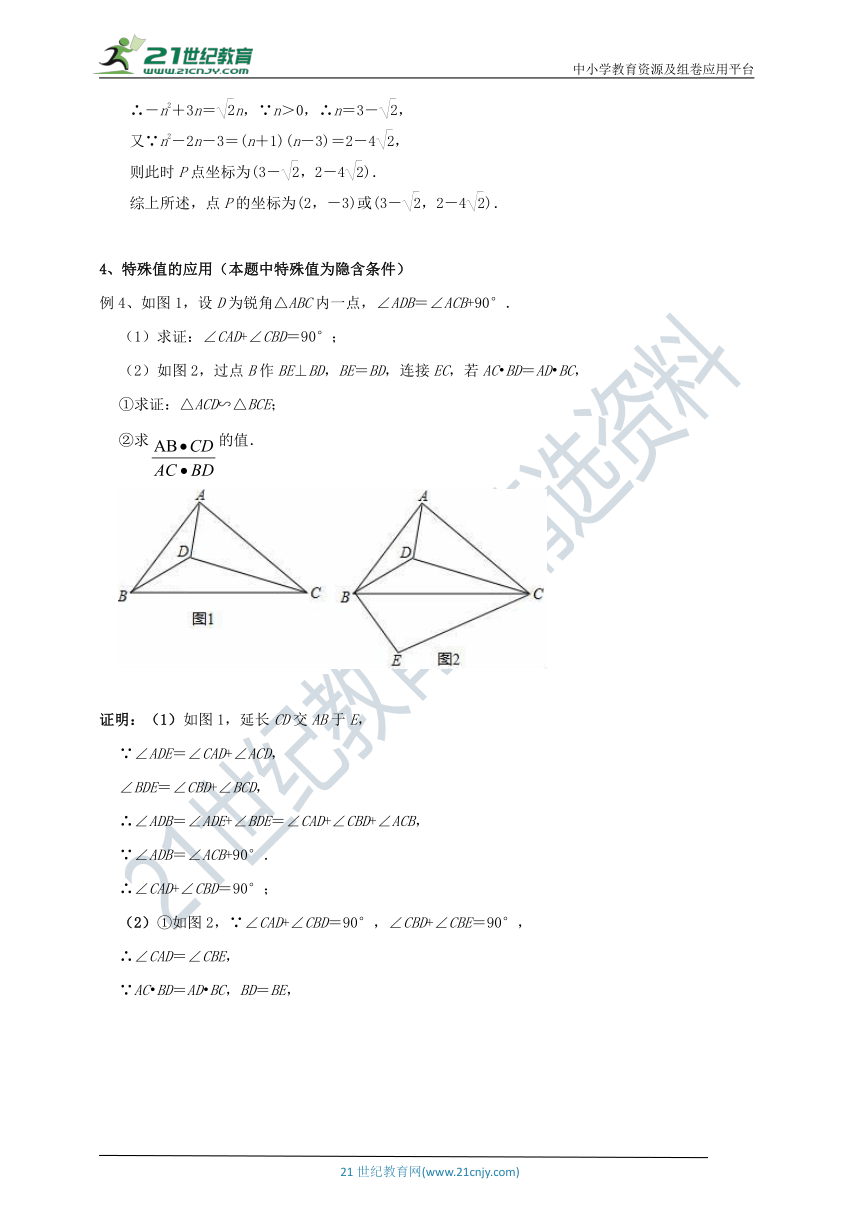
例4、如图1,设D为锐角△ABC内一点,∠ADB=∠ACB+90°.
(1)求证:∠CAD+∠CBD=90°;
(2)如图2,过点B作BE⊥BD,BE=BD,连接EC,若AC BD=AD BC,
①求证:△ACD∽△BCE;
②求的值.
证明:(1)如图1,延长CD交AB于E,
∵∠ADE=∠CAD+∠ACD,
∠BDE=∠CBD+∠BCD,
∴∠ADB=∠ADE+∠BDE=∠CAD+∠CBD+∠ACB,
∵∠ADB=∠ACB+90°.
∴∠CAD+∠CBD=90°;
(2)①如图2,∵∠CAD+∠CBD=90°,∠CBD+∠CBE=90°,
∴∠CAD=∠CBE,
∵AC BD=AD BC,BD=BE,
∴
∴△ACD∽△BCE;
②如图2,连接DE,
∵BE⊥BD,BE=BD,
∴△BDE是等腰直角三角形,
∴(首先算出本题中隐含的特殊值,连接DE,构造等腰直角三角形)
∵△ACD∽△BCE,
∴∠ACD=∠BCE,
∴∠ACB=∠DCE,
∵
∴△ACB∽△DCE,
∴
∴
新增:
如图1,在平面直角坐标系中将y=2x+1向下平移3个单位长度得到直线l1,直线l1与x轴交于点C;直线l2:y=x+2与x轴、y轴交于A、B两点,且与直线l1交于点D.
(1)填空:点A的坐标为 ,点B的坐标为 ;
(2)直线l1的表达式为 ;
(3)在直线l1上是否存在点E,使S△AOE=2S△ABO?若存在,则求出点E的坐标;若不存在,请说明理由.
(4)如图2,点P为线段AD上一点(不含端点),连接CP,一动点H从C出发,沿线段CP以每秒1个单位的速度运动到点P,再沿线段PD以每秒个单位的速度运动到点D后停止,求点H在整个运动过程中所用时间最少时点P的坐标.
如图1,在平面直角坐标系中将y=2x+1向下平移3个单位长度得到直线l1,直线l1与x轴交于点C;直线l2:y=x+2与x轴、y轴交于A、B两点,且与直线l1交于点D.
(1)填空:点A的坐标为 (﹣2,0) ,点B的坐标为 (0,2) ;
(2)直线l1的表达式为 y=2x﹣2 ;
(3)在直线l1上是否存在点E,使S△AOE=2S△ABO?若存在,则求出点E的坐标;若不存在,请说明理由.
(4)如图2,点P为线段AD上一点(不含端点),连接CP,一动点H从C出发,沿线段CP以每秒1个单位的速度运动到点P,再沿线段PD以每秒个单位的速度运动到点D后停止,求点H在整个运动过程中所用时间最少时点P的坐标.
【分析】(1)直线l2:y=x+2,令y=0,则x=﹣2,令y=0,则x=2,即可求解;
(2)根据平移的性质即可求解;
(3)S△AOE=2S△ABO,即:yE=2OB=4,即可求解;
(4)点H在整个运动过程中所用时间=+=PH+PC,当C、P、H在一条直线上时,PH+PC最小,即可求解.
【解答】解:(1)直线l2:y=x+2,令y=0,则x=﹣2,令y=0,则x=2,
故答案为(﹣2,0)、(0,2);
(2)y=2x+1向下平移3个单位长度得到直线l1,则直线l1的表达式为:y=2x﹣2,
故:答案为:y=2x﹣2;
(3)∵S△AOE=2S△ABO,
∴yE=2OB=±4,
将yE=4代入l1的表达式得:±4=2x﹣2,解得:x=3或﹣1,
则点E的坐标为(3,4)或(﹣1,﹣4);
(4)过点P、C分别作y轴的平行线,分别交过点D作x轴平行线于点H、H′,H′C交BD于点P′,
直线l2:y=x+2,则∠ABO=45°=∠HBD,PH=PD,
点H在整个运动过程中所用时间=+=PH+PC,
当C、P、H在一条直线上时,PH+PC最小,即为CH′=6,点P坐标(1,3),
故:点H在整个运动过程中所用最少时间为6秒,此时点P的坐标(1,3).
【点评】本题为一次函数综合题,主要考查了面积的计算方法、解直角三角形、点的对称性等,其中(4),所用的时间=+=PH+PC,是本题的难点,也是解此类问题的一种基本方法.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
初中几何:特殊角或特殊值在解题时的妙用
初中数学 九年级上期末 或中考一轮复习专用
在解几何题时,我们常常会碰到一些特殊角:30 、45 、60 ,还有一些特殊数值:
,,。
不过有时还可能出现以下两种情况:
①有时特殊角是15 ,那么我们可以适当变换:15 =45 -30 =60 -45 ,或者利用倍角30 =2×15 (通常要用到外角定理);
②有时题目中特殊角或特殊值没有明确给出,比较隐含,需要我们去挖掘。
碰到含有这些特殊值的题目时,应该怎么办?不用怕,其实,这种题目有很强的解题方法和技巧!
当看到这些特殊角/值时,一般情况下,我们不用多想:直接利用特殊角或特殊值所表示的角或线段,构造直角三角形或等边三角形。
1、30°/60 特殊角的应用
例1、如图,平行四边形ABCD的对角线AC,BD相交于点O,AB=5,BC=6.
(1)求OD长的取值范围;
(2)若∠CBD=30°,求OD的长.
解:(1)提示:∵CD=5,BC=6,1<BD<11,OD为BD的一半
∴
(2)过C作CE⊥BD于E,(因为∠CBD=30°为特殊角,那么我们直接过点C作CE⊥BD,构造两个直角三角形)
Rt△CBE中,∵∠CBD=30°,BC=6,
∴CE=3,BE==3,
在Rt△CED中,CD2=DE2+CE2,
代入CD、CE的值,解得:DE=4,
∴BD=BE+DE=3+4,
∴OD=BD=+2,
则OD的长是+2.
2、45°特殊角的应用
例2、如图,已知点B(0,2),A(﹣6,﹣1)在反比例函数的图象上,作射线AB,再将射线AB绕点A逆时针旋转45°后,交反比例函数图象于点C,则点C的坐标为 .
解:如图所示,过B作BD⊥AC于D,(因为∠CBD=30°为特殊角,那么我们直接过点C作CE⊥BD,构造两个直角三角形)
过D作DE⊥y轴于E,过A作AF⊥DE于F,则△ABD为等腰直角三角形,易得△AFD ≌△DEB,
设DF=BE=a,
∵B(0,2),A(﹣6,﹣1),
∴OE=a+2=GF,DE=6﹣a,AF=a+3,
∵AF=DE,
∴a+3=6﹣a,
解得a=,
∴D(,),
设直线AD的解析式为y=k'x+b,则
代入AD两点坐标,
解得,
∴y=3x+17,
∵A(﹣6,﹣1)在反比例函数的图象上,
∴k=6,即y=,
解方程组,可得或,
∴点C的坐标为(,18),
故答案为:(,18).
有时候题目条件中没有直接给出特殊角或特殊值 ,但根据经验,可以从条件中可以根据条件,分析得到特殊角
例3、如图,已知二次函数y=ax2+bx+c的图象与x轴相交于A(-1,0),B(3,0)两点, 与y轴相交于点C(0,-3).
(1)求这个二次函数的表达式;
(2)若P是第四象限内这个二次函数的图象上任意一点,PH⊥x轴于点H,与BC交于点M,连接PC.
①求线段PM的最大值;
②当△PCM是以PM为一腰的等腰三角形时,求点P的坐标.
本题重要思想方法:
1)二次函数中,求线段的最值,通常将其转化为求二次函数的最值问题。(转化的思想)
2)注意特殊角的应用。本题为45 特殊角(等腰三角形中,底角为45 ,那么顶角为90 )
解:(1)二次函数的表达式为y=x2-2x-3.
(2)①设直线BC的表达式为y=kx+t,
将B,C的坐标分别代入函数表达式,得k=-1,t=-3
∴直线BC的表达式为y=x-3.
设M(n,n-3),则P(n,n2-2n-3),
PM=(n-3)-(n2-2n-3)=-n2+3n=-+(0<n<3),
当n=时,PM最大=;
②满足题意的有PM=PC和PM=CM两种情况:
(在直角坐标系中,因为OB=OC,那么∠OCB=45°,此题特殊角比较隐含,但却对本题解决问题起到至关重要的作用)
(Ⅰ)如图①,当PM=PC时,∵OB=OC,PH⊥x轴,
∴∠PMC=∠OCB=45°,又∵PM=PC,∴△PCM是等腰直角三角形,∴PC∥x轴,∴点P与C(0,-3)关于y=x2-2x-3的对称轴x=1对称,此时点P的坐标为(2,-3);
(Ⅱ)如图②,当PM=CM时,作MN∥x轴,则CM=MN=n,
∴-n2+3n=n,∵n>0,∴n=3-,
又∵n2-2n-3=(n+1)(n-3)=2-4,
则此时P点坐标为(3-,2-4).
综上所述,点P的坐标为(2,-3)或(3-,2-4).
4、特殊值的应用(本题中特殊值为隐含条件)
例4、如图1,设D为锐角△ABC内一点,∠ADB=∠ACB+90°.
(1)求证:∠CAD+∠CBD=90°;
(2)如图2,过点B作BE⊥BD,BE=BD,连接EC,若AC BD=AD BC,
①求证:△ACD∽△BCE;
②求的值.
证明:(1)如图1,延长CD交AB于E,
∵∠ADE=∠CAD+∠ACD,
∠BDE=∠CBD+∠BCD,
∴∠ADB=∠ADE+∠BDE=∠CAD+∠CBD+∠ACB,
∵∠ADB=∠ACB+90°.
∴∠CAD+∠CBD=90°;
(2)①如图2,∵∠CAD+∠CBD=90°,∠CBD+∠CBE=90°,
∴∠CAD=∠CBE,
∵AC BD=AD BC,BD=BE,
∴
∴△ACD∽△BCE;
②如图2,连接DE,
∵BE⊥BD,BE=BD,
∴△BDE是等腰直角三角形,
∴(首先算出本题中隐含的特殊值,连接DE,构造等腰直角三角形)
∵△ACD∽△BCE,
∴∠ACD=∠BCE,
∴∠ACB=∠DCE,
∵
∴△ACB∽△DCE,
∴
∴
新增:
如图1,在平面直角坐标系中将y=2x+1向下平移3个单位长度得到直线l1,直线l1与x轴交于点C;直线l2:y=x+2与x轴、y轴交于A、B两点,且与直线l1交于点D.
(1)填空:点A的坐标为 ,点B的坐标为 ;
(2)直线l1的表达式为 ;
(3)在直线l1上是否存在点E,使S△AOE=2S△ABO?若存在,则求出点E的坐标;若不存在,请说明理由.
(4)如图2,点P为线段AD上一点(不含端点),连接CP,一动点H从C出发,沿线段CP以每秒1个单位的速度运动到点P,再沿线段PD以每秒个单位的速度运动到点D后停止,求点H在整个运动过程中所用时间最少时点P的坐标.
如图1,在平面直角坐标系中将y=2x+1向下平移3个单位长度得到直线l1,直线l1与x轴交于点C;直线l2:y=x+2与x轴、y轴交于A、B两点,且与直线l1交于点D.
(1)填空:点A的坐标为 (﹣2,0) ,点B的坐标为 (0,2) ;
(2)直线l1的表达式为 y=2x﹣2 ;
(3)在直线l1上是否存在点E,使S△AOE=2S△ABO?若存在,则求出点E的坐标;若不存在,请说明理由.
(4)如图2,点P为线段AD上一点(不含端点),连接CP,一动点H从C出发,沿线段CP以每秒1个单位的速度运动到点P,再沿线段PD以每秒个单位的速度运动到点D后停止,求点H在整个运动过程中所用时间最少时点P的坐标.
【分析】(1)直线l2:y=x+2,令y=0,则x=﹣2,令y=0,则x=2,即可求解;
(2)根据平移的性质即可求解;
(3)S△AOE=2S△ABO,即:yE=2OB=4,即可求解;
(4)点H在整个运动过程中所用时间=+=PH+PC,当C、P、H在一条直线上时,PH+PC最小,即可求解.
【解答】解:(1)直线l2:y=x+2,令y=0,则x=﹣2,令y=0,则x=2,
故答案为(﹣2,0)、(0,2);
(2)y=2x+1向下平移3个单位长度得到直线l1,则直线l1的表达式为:y=2x﹣2,
故:答案为:y=2x﹣2;
(3)∵S△AOE=2S△ABO,
∴yE=2OB=±4,
将yE=4代入l1的表达式得:±4=2x﹣2,解得:x=3或﹣1,
则点E的坐标为(3,4)或(﹣1,﹣4);
(4)过点P、C分别作y轴的平行线,分别交过点D作x轴平行线于点H、H′,H′C交BD于点P′,
直线l2:y=x+2,则∠ABO=45°=∠HBD,PH=PD,
点H在整个运动过程中所用时间=+=PH+PC,
当C、P、H在一条直线上时,PH+PC最小,即为CH′=6,点P坐标(1,3),
故:点H在整个运动过程中所用最少时间为6秒,此时点P的坐标(1,3).
【点评】本题为一次函数综合题,主要考查了面积的计算方法、解直角三角形、点的对称性等,其中(4),所用的时间=+=PH+PC,是本题的难点,也是解此类问题的一种基本方法.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://21世纪教育网(www.21cnjy.com)
" 21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 特殊平行四边形
- 1 菱形的性质与判定
- 2 矩形的性质与判定
- 3 正方形的性质与判定
- 第二章 一元二次方程
- 1 认识一元二次方程
- 2 用配方法求解一元二次方程
- 3 用公式法求解一元二次方程
- 4 用因式分解法求解一元二次方程
- 5 一元二次方程的根与系数的关系
- 6 应用一元二次方程
- 第三章 概率的进一步认识
- 1 用树状图或表格求概率
- 2 用频率估计概率
- 第四章 图形的相似
- 1 成比例线段
- 2 平行线分线段成比例
- 3 相似多边形
- 4 探索三角形相似的条件
- 5 相似三角形判定定理的证明
- 6 利用相似三角形测高
- 7 相似三角形的性质
- 8 图形的位似
- 第五章 投影与视图
- 1 投影
- 2 视图
- 第六章 反比例函数
- 1 反比例函数
- 2 反比例函数的图象与性质
- 3 反比例函数的应用
