鲁教版(五四学制)数学六年级上册 4.2解一元一次方程(1) 课件(25张)
文档属性
| 名称 | 鲁教版(五四学制)数学六年级上册 4.2解一元一次方程(1) 课件(25张) |  | |
| 格式 | pptx | ||
| 文件大小 | 276.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 08:35:45 | ||
图片预览







文档简介
(共25张PPT)
4.2 解一元一次方程(1)
(1) x-2x+4x
(2)5y+y-2y
(3)2a-1.5a-0.5a
=(1-2+4)x
=3x
=(5+1 -2)y
=4y
=(2-1.5-0.5)a
合并同类项
=0
知识准备
解下列方程
(1)x-4=29
(2)-x+4=29
(3)
2
2
5
5
= -
x
(1) X=33
(2) X=-25
(3)
知识准备
应用等式的性质解方程
问题1:
某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍,前年这个学校购买了多少台计算机?
设前年购买x台。可以表示出:去年购买计算机 台,今年购买计算机 台。你能找出问题中的相等关系吗?
2 x
4 x
前年购买量+去年购买量+今年购买量=140台
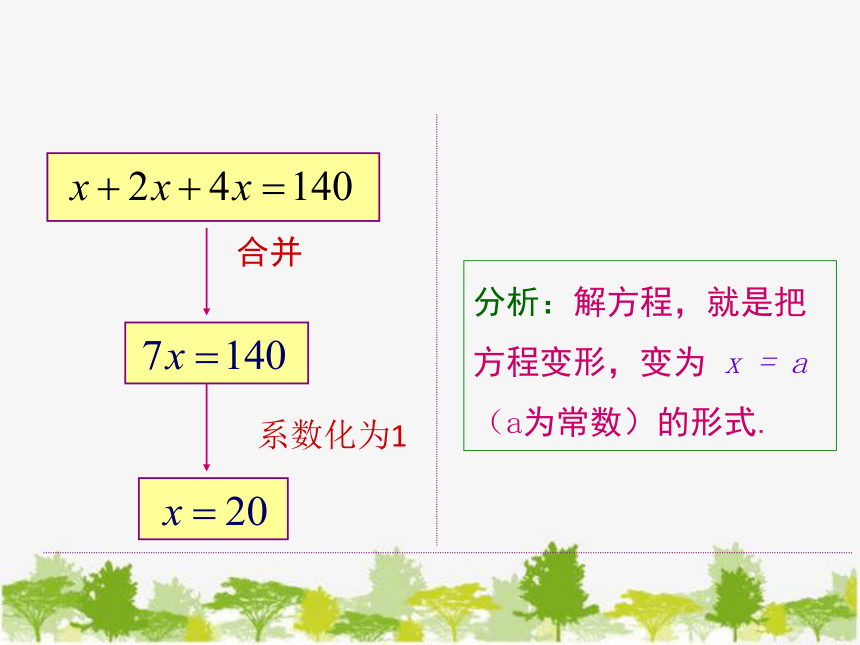
x+2x+4x=140
“总量=各部分量的和”是一个基本的相等关系.
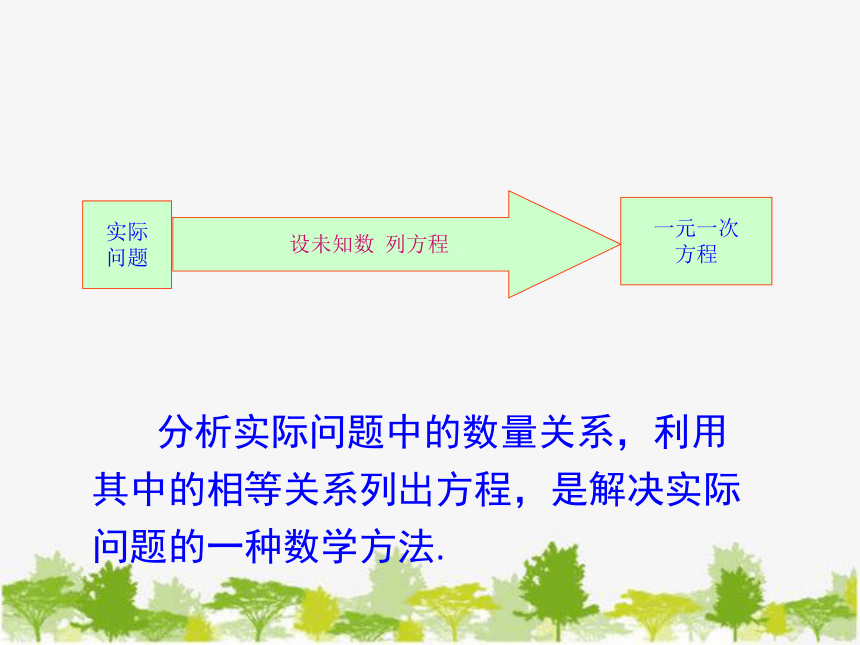
实际
问题
一元一次
方程
分析实际问题中的数量关系,利用其中的相等关系列出方程,是解决实际问题的一种数学方法.
设未知数 列方程
分析:解方程,就是把方程变形,变为 x = a(a为常数)的形式.
合并
系数化为1
解方程中“合并”起了什么作用?
解方程中的“合并”是利用分配律将含有未知数的项和常数项分别合并为一项.它使方程变得简单,更接近x = a的形式.
思考?
解:合并同类项,得
2x=-10
系数化为1,得
x=-5.
例1:解方程
(1)5x-3x=-10
例题解析
解:合并同类项,得
系数化为1,得
X=60
例题变式:
解方程:
合并同类项
系数化成1
x=5
2x=-10
5x-3x=-10
解简单方程的步骤
1、小明在解方程3x–4x=7时,是这样写解的过程的:
3x–4x=7=-x=7=x=-7
(1)小明这样写对不对?
(2)应该怎样写?
练习
2、解下列方程
(1)x-3x=-4
(2) -x+3x=4
(3) 3x-x=8-0.5×8
(4) -x+3x-6=-2
注意: 1.解方程的步骤的格式
2.符号合并时的符号问题.
3.已知:y1 = 2x+1, y2 = 4 -5x.当x取何值时, y1 + y2= -7?
解:由题意,得
2x+1+ 4 -5x =-7
合并同类项,得 - 3x+5=-7
两边减5,得 - 3x=-12
系数化为1,得 x=4.
所以当x=4时, y1 = y2 .
例2:有一列整数,按一定的规律成 1,-3,9,
-27,81,···,其中某三个相邻数的和为-1701,这三个数各是多少
解:设这三个相邻数中的第1个数为x,
那么第2个数就是-3x,
第3个数就是-3×(-3x)=9x.
根据这三个数的和是-1701,得
x-3x+9x=-1701
合并同类项,得
7x=-1701
系数化为1,得
x=-243.
所以 -3x=729,
9x=-2187
答:这三个数是-243,729,-2187
注意:应用题要作“答”哟!
1、 有一列整数,按一定的规律成 2,-4,8,-16,32, -64,···,
(1)试写出第8、第9个数分别是多少?
(2)如果2是这组第一个数,-4是第二个数,,8是第三个数···那么第n个数是什么?试用n表示出来。
(3)若其中某三个相邻数的和为1 536,这三个数各是多少
( 4)若其中四个相邻数的和可能为-2014吗?
例题变式:
解:(1)第8第9个数分别是128、-256
(2)
( 3)设这三个相邻数中的第1个数为x,
那么第2个数就是-2x,
第3个数就是-2×(-2x)=4x.
根据这三个数的和是1536,得
x-2x+4x=1 536.
(4)相邻四个数的和为:x-2x+4x-8x=-5x,一定是
5的倍数,不可能等于-2014
合并同类项,得
3x=1 536.
系数化为1,得
x=512.
所以 -2x=-1 024,
4x=2 048.
答:这三个数是512、-1 024、2 048.
2、有一列整数,按一定的规律成3,5,9,17,33,65, ···试写出第8、第9个数分别是多少? (1)如果是这组第一个数,5是第二个数,,9是第三个数···那么第n个数是什么?试用n表示出来.
(2)若其中某三个相邻数的和为227,这三个数各是多少
1.简单方程解法步骤
合并同类项;
系数化为1.
小 结
2.用一元一次方程分析并解决实际问题的基本过程:
实际问题
数学问题
(一元一次方程)
实际问题
的答案
数学问题的解
(x=a)
检验
列方程
解方程
1. 若方程x+9=8的解也是方程ax+3x=7解,则a= ______.
2.若x=4是方程 的解,则
的值为__________.
-10
10
练习
3.解下列方程.
(1) 、-3x+0.5x=10
(2)、7x-4.5x+1=2.5×3-5
4. 有一列整数,按一定的规律成,2,4,6,8,,10,12, 6···若其中某三个相邻数的和为6042,这三个数各是多少
练习
5.在某月内,李老师要参加三天的学习培训,现在知道这三天的日期的数字之和是39.
(1)培训时间是连续的三天,你知道这几天分别是当月的哪几号吗?
(2)若培训时间是连续三周的周六,那这几天又分是当月的哪几号?
(1)12、13、14
(2)6、13、20
练习
4.2 解一元一次方程(1)
(1) x-2x+4x
(2)5y+y-2y
(3)2a-1.5a-0.5a
=(1-2+4)x
=3x
=(5+1 -2)y
=4y
=(2-1.5-0.5)a
合并同类项
=0
知识准备
解下列方程
(1)x-4=29
(2)-x+4=29
(3)
2
2
5
5
= -
x
(1) X=33
(2) X=-25
(3)
知识准备
应用等式的性质解方程
问题1:
某校三年共购买计算机140台,去年购买数量是前年的2倍,今年购买数量又是去年的2倍,前年这个学校购买了多少台计算机?
设前年购买x台。可以表示出:去年购买计算机 台,今年购买计算机 台。你能找出问题中的相等关系吗?
2 x
4 x
前年购买量+去年购买量+今年购买量=140台
x+2x+4x=140
“总量=各部分量的和”是一个基本的相等关系.
实际
问题
一元一次
方程
分析实际问题中的数量关系,利用其中的相等关系列出方程,是解决实际问题的一种数学方法.
设未知数 列方程
分析:解方程,就是把方程变形,变为 x = a(a为常数)的形式.
合并
系数化为1
解方程中“合并”起了什么作用?
解方程中的“合并”是利用分配律将含有未知数的项和常数项分别合并为一项.它使方程变得简单,更接近x = a的形式.
思考?
解:合并同类项,得
2x=-10
系数化为1,得
x=-5.
例1:解方程
(1)5x-3x=-10
例题解析
解:合并同类项,得
系数化为1,得
X=60
例题变式:
解方程:
合并同类项
系数化成1
x=5
2x=-10
5x-3x=-10
解简单方程的步骤
1、小明在解方程3x–4x=7时,是这样写解的过程的:
3x–4x=7=-x=7=x=-7
(1)小明这样写对不对?
(2)应该怎样写?
练习
2、解下列方程
(1)x-3x=-4
(2) -x+3x=4
(3) 3x-x=8-0.5×8
(4) -x+3x-6=-2
注意: 1.解方程的步骤的格式
2.符号合并时的符号问题.
3.已知:y1 = 2x+1, y2 = 4 -5x.当x取何值时, y1 + y2= -7?
解:由题意,得
2x+1+ 4 -5x =-7
合并同类项,得 - 3x+5=-7
两边减5,得 - 3x=-12
系数化为1,得 x=4.
所以当x=4时, y1 = y2 .
例2:有一列整数,按一定的规律成 1,-3,9,
-27,81,···,其中某三个相邻数的和为-1701,这三个数各是多少
解:设这三个相邻数中的第1个数为x,
那么第2个数就是-3x,
第3个数就是-3×(-3x)=9x.
根据这三个数的和是-1701,得
x-3x+9x=-1701
合并同类项,得
7x=-1701
系数化为1,得
x=-243.
所以 -3x=729,
9x=-2187
答:这三个数是-243,729,-2187
注意:应用题要作“答”哟!
1、 有一列整数,按一定的规律成 2,-4,8,-16,32, -64,···,
(1)试写出第8、第9个数分别是多少?
(2)如果2是这组第一个数,-4是第二个数,,8是第三个数···那么第n个数是什么?试用n表示出来。
(3)若其中某三个相邻数的和为1 536,这三个数各是多少
( 4)若其中四个相邻数的和可能为-2014吗?
例题变式:
解:(1)第8第9个数分别是128、-256
(2)
( 3)设这三个相邻数中的第1个数为x,
那么第2个数就是-2x,
第3个数就是-2×(-2x)=4x.
根据这三个数的和是1536,得
x-2x+4x=1 536.
(4)相邻四个数的和为:x-2x+4x-8x=-5x,一定是
5的倍数,不可能等于-2014
合并同类项,得
3x=1 536.
系数化为1,得
x=512.
所以 -2x=-1 024,
4x=2 048.
答:这三个数是512、-1 024、2 048.
2、有一列整数,按一定的规律成3,5,9,17,33,65, ···试写出第8、第9个数分别是多少? (1)如果是这组第一个数,5是第二个数,,9是第三个数···那么第n个数是什么?试用n表示出来.
(2)若其中某三个相邻数的和为227,这三个数各是多少
1.简单方程解法步骤
合并同类项;
系数化为1.
小 结
2.用一元一次方程分析并解决实际问题的基本过程:
实际问题
数学问题
(一元一次方程)
实际问题
的答案
数学问题的解
(x=a)
检验
列方程
解方程
1. 若方程x+9=8的解也是方程ax+3x=7解,则a= ______.
2.若x=4是方程 的解,则
的值为__________.
-10
10
练习
3.解下列方程.
(1) 、-3x+0.5x=10
(2)、7x-4.5x+1=2.5×3-5
4. 有一列整数,按一定的规律成,2,4,6,8,,10,12, 6···若其中某三个相邻数的和为6042,这三个数各是多少
练习
5.在某月内,李老师要参加三天的学习培训,现在知道这三天的日期的数字之和是39.
(1)培训时间是连续的三天,你知道这几天分别是当月的哪几号吗?
(2)若培训时间是连续三周的周六,那这几天又分是当月的哪几号?
(1)12、13、14
(2)6、13、20
练习
