2021--2022学年冀教版数学九年级上册26.4解直角三角形的应用课件(21张)
文档属性
| 名称 | 2021--2022学年冀教版数学九年级上册26.4解直角三角形的应用课件(21张) |  | |
| 格式 | pptx | ||
| 文件大小 | 322.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 冀教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 08:40:02 | ||
图片预览


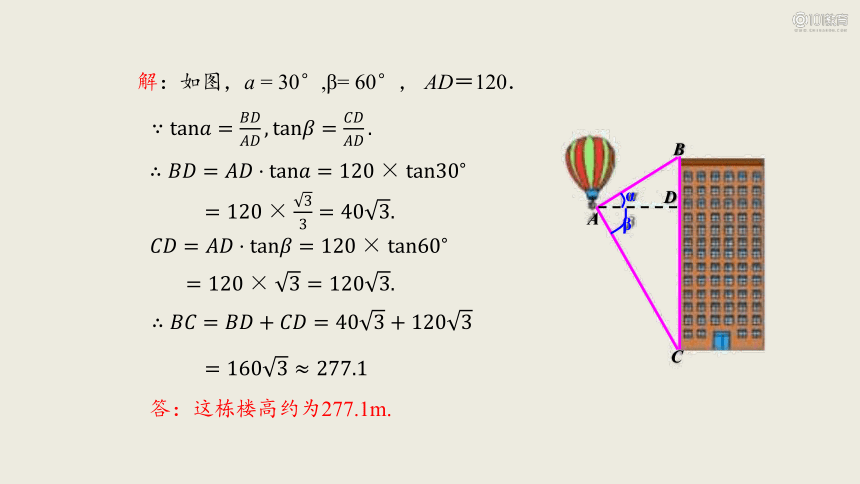


文档简介
(共21张PPT)
26.4 解直角三角形的应用
1.复习并巩固解直角三角形的相关知识.
2.能够解决与仰角、俯角有关的实际问题. (重点、难点)
3.能够解决与坡度、坡角有关的实际问题. (重点、难点)
学习目标
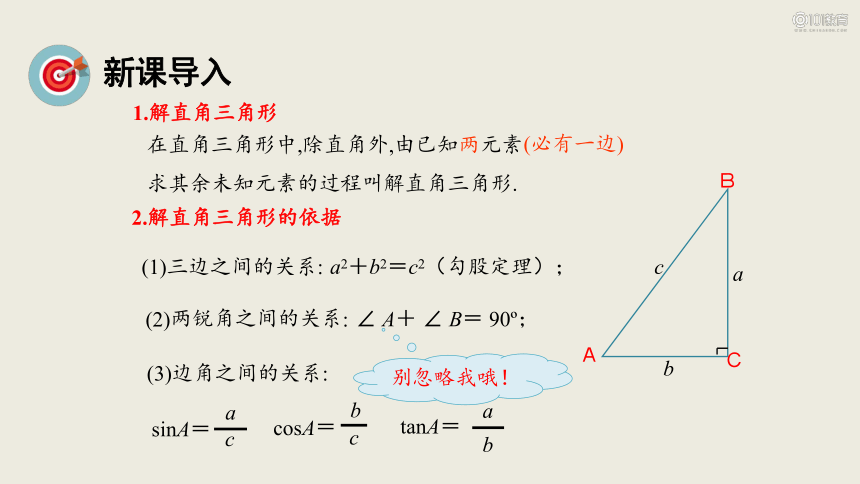
在直角三角形中,除直角外,由已知两元素
求其余未知元素的过程叫解直角三角形.
1.解直角三角形
(1)三边之间的关系:
a2+b2=c2(勾股定理);
2.解直角三角形的依据
(2)两锐角之间的关系:
∠ A+ ∠ B= 90 ;
(3)边角之间的关系:
tanA=
a
b
sinA=
a
c
cosA=
b
c
(必有一边)
A
C
B
a
b
c
别忽略我哦!
新课导入
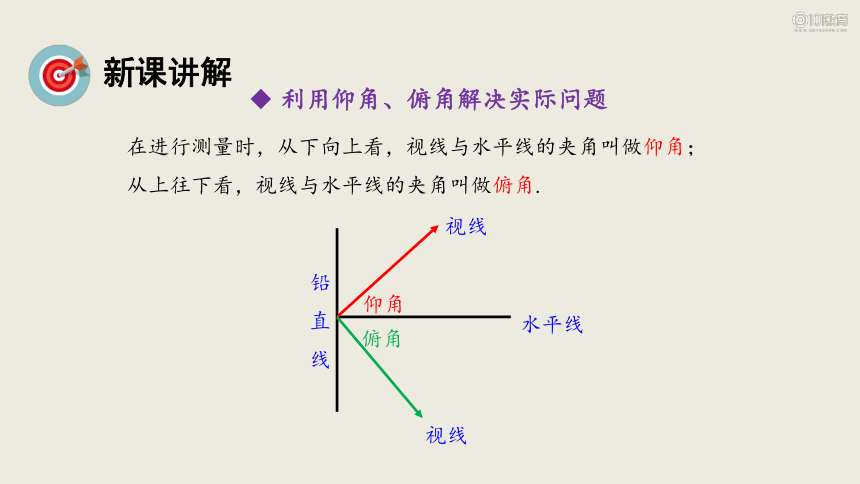
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
利用仰角、俯角解决实际问题
新课讲解
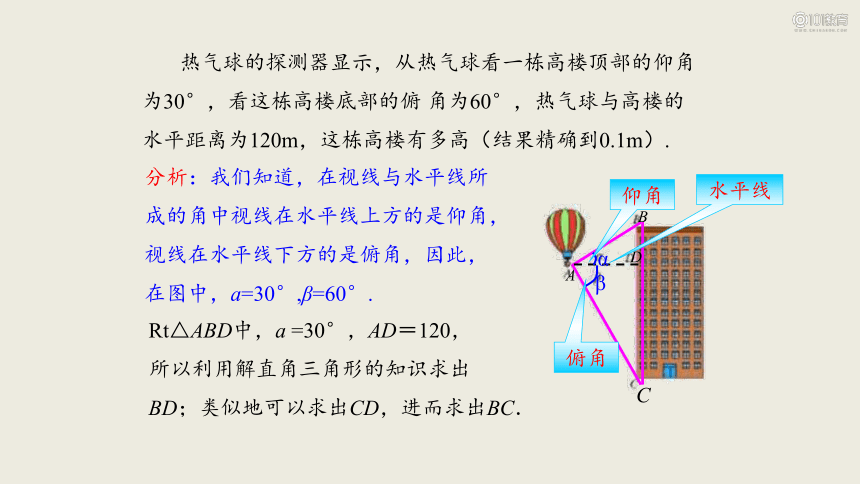
热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯 角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m).
分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,a=30°,β=60°.
Rt△ABD中,a =30°,AD=120,
所以利用解直角三角形的知识求出
BD;类似地可以求出CD,进而求出BC.
A
B
C
D
α
β
仰角
水平线
俯角
解:如图,a = 30°,β= 60°, AD=120.
答:这栋楼高约为277.1m.
A
B
C
D
α
β
建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶部A的仰角54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).
A
B
C
D
40m
54°
45°
解:在等腰三角形BCD中∠ACD=90°,
BC=DC=40m.
在Rt△ACD中
所以AB=AC-BC=55.2-40=15.2.
答:棋杆的高度为15.2m.
利用坡度、坡角解决实际问题
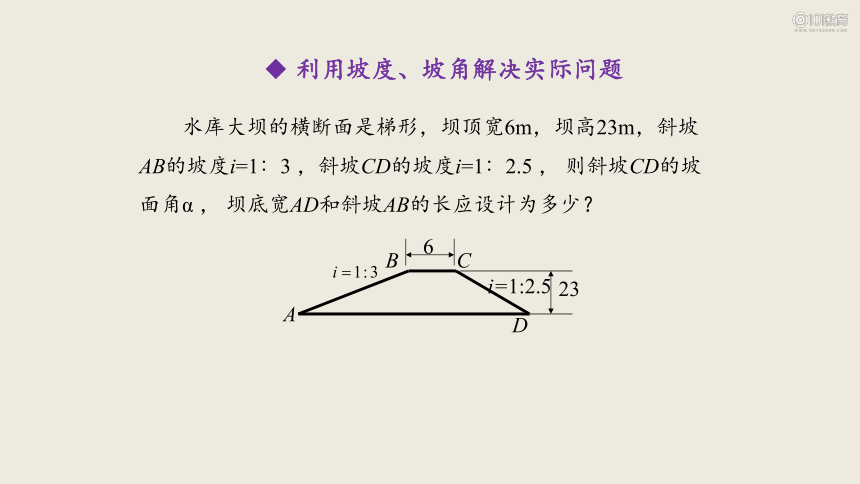
水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3 ,斜坡CD的坡度i=1∶2.5 , 则斜坡CD的坡面角α , 坝底宽AD和斜坡AB的长应设计为多少?
A
D
B
C
i=1:2.5
23
6
α
l
h
i= h : l
1.坡角
坡面与水平面的夹角叫做坡角,记作α .
2.坡度(或坡比)
坡度通常写成1∶m的形式,如i=1∶6.
如图所示,坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面的坡度(或坡比),记作i, 即
3.坡度与坡角的关系
坡度等于坡角的正切值
坡面
水平面
1.斜坡的坡度是 ,则坡角α=______度.
2.斜坡的坡角是45° ,则坡比是 _______.
3.斜坡长是12米,坡高6米,则坡比是_______.
α
l
h
30
1:1
例:水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,求:
(1)坝底AD与斜坡AB的长度(精确到0.1m );
(2)斜坡CD的坡角α(精确到 1°).
E
F
A
D
B
C
i=1:2.5
23
6
α
分析:由坡度i会想到产生铅垂高度,即分别过点B、C 作AD的垂线;
垂线BE、CF将梯形分割成Rt△ABE,Rt△CFD和矩形BEFC,则AD=AE+EF+FD, EF=BC=6m,AE、DF可结合坡度,通过解Rt△ABE和Rt△CDF求出;
斜坡AB的长度以及斜坡CD的坡角的问题实质上就是解Rt△ ABE和Rt△ CDF.
解:(1)分别过点B、C作BE⊥AD,CF⊥AD,垂足分别为点E、 F,由题意可知
E
F
A
D
B
C
i=1:2.5
23
6
α
BE=CF=23m , EF=BC=6m.
在Rt△ABE中
在Rt△DCF中,同理可得
=69+6+57.5=132.5m.
在Rt△ABE中,由勾股定理可得
(2) 斜坡CD的坡度i=tanα=1:2.5=0.4,
由计算器可算得
答:坝底宽AD为132.5米,斜坡AB的长约为72.7米.斜坡CD的坡角α约为22°.
如图,拦水坝的横断面为梯形ABCD(图中i=1:3是指坡面的铅直高度DE与水平宽度CE的比),根据图中数据求:
(1)坡角a和β;
(2)坝顶宽AD和斜坡AB的长(精确到0.1m).
B
A
D
F
E
C
6m
α
β
i=1:3
i=1:1.5
解:(1)在Rt△AFB中,∠AFB=90°
在Rt△CDE中,∠CED=90°
完成第(2)题
1.如图(2),在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC=_________米.
2.如图(3),两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为_____米.
100
随堂练习
3.如图3,从地面上的C,D两点测得树顶A仰角分别是45°和30°,已知CD=200米,点C在BD上,则树高AB等于 (根号保留).
4.如图4,将宽为1cm的纸条沿BC折叠,使∠CAB=45°,则折叠后重叠部分的面积为 (根号保留).
图3
图4
5.一段路基的横断面是梯形,高为4米,上底的宽是12米,路基的坡面与地面的倾角分别是45°和30°,求路基下底的宽(精确到0.1米, ).
45°
30°
4米
12米
A
B
C
E
F
D
解:作DE⊥AB,CF⊥AB,垂足分别为E、F.由题意可知
DE=CF=4(米),
CD=EF=12(米).
在Rt△ADE中,
在Rt△BCF中,同理可得
因此AB=AE+EF+BF≈4+12+6.93≈22.93(米).
答: 路基下底的宽约为22.93米.
45°
30°
4米
12米
A
B
C
E
F
D
6.如下图,在一次数学课外活动中,测得电线杆底部B与钢缆固定点O的距离为4米,钢缆与地面的夹角∠BOA为60 ,则这条钢缆在电线杆上的固定点A到地面的距离AB是多少米(结果保留根号).
解:在Rt△ABO中,
∵tan∠BOA= =tan60°=
∴AB=BO tan60°=4 ×=4 (米)
答:这条钢缆在电线杆上的固定点A到地面的距离AB是4 米.
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
课堂小结
26.4 解直角三角形的应用
1.复习并巩固解直角三角形的相关知识.
2.能够解决与仰角、俯角有关的实际问题. (重点、难点)
3.能够解决与坡度、坡角有关的实际问题. (重点、难点)
学习目标
在直角三角形中,除直角外,由已知两元素
求其余未知元素的过程叫解直角三角形.
1.解直角三角形
(1)三边之间的关系:
a2+b2=c2(勾股定理);
2.解直角三角形的依据
(2)两锐角之间的关系:
∠ A+ ∠ B= 90 ;
(3)边角之间的关系:
tanA=
a
b
sinA=
a
c
cosA=
b
c
(必有一边)
A
C
B
a
b
c
别忽略我哦!
新课导入
铅直线
水平线
视线
视线
仰角
俯角
在进行测量时,从下向上看,视线与水平线的夹角叫做仰角;
从上往下看,视线与水平线的夹角叫做俯角.
利用仰角、俯角解决实际问题
新课讲解
热气球的探测器显示,从热气球看一栋高楼顶部的仰角为30°,看这栋高楼底部的俯 角为60°,热气球与高楼的水平距离为120m,这栋高楼有多高(结果精确到0.1m).
分析:我们知道,在视线与水平线所成的角中视线在水平线上方的是仰角,视线在水平线下方的是俯角,因此,在图中,a=30°,β=60°.
Rt△ABD中,a =30°,AD=120,
所以利用解直角三角形的知识求出
BD;类似地可以求出CD,进而求出BC.
A
B
C
D
α
β
仰角
水平线
俯角
解:如图,a = 30°,β= 60°, AD=120.
答:这栋楼高约为277.1m.
A
B
C
D
α
β
建筑物BC上有一旗杆AB,由距BC40m的D处观察旗杆顶部A的仰角54°,观察底部B的仰角为45°,求旗杆的高度(精确到0.1m).
A
B
C
D
40m
54°
45°
解:在等腰三角形BCD中∠ACD=90°,
BC=DC=40m.
在Rt△ACD中
所以AB=AC-BC=55.2-40=15.2.
答:棋杆的高度为15.2m.
利用坡度、坡角解决实际问题
水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3 ,斜坡CD的坡度i=1∶2.5 , 则斜坡CD的坡面角α , 坝底宽AD和斜坡AB的长应设计为多少?
A
D
B
C
i=1:2.5
23
6
α
l
h
i= h : l
1.坡角
坡面与水平面的夹角叫做坡角,记作α .
2.坡度(或坡比)
坡度通常写成1∶m的形式,如i=1∶6.
如图所示,坡面的铅垂高度(h)和水平长度(l)
的比叫做坡面的坡度(或坡比),记作i, 即
3.坡度与坡角的关系
坡度等于坡角的正切值
坡面
水平面
1.斜坡的坡度是 ,则坡角α=______度.
2.斜坡的坡角是45° ,则坡比是 _______.
3.斜坡长是12米,坡高6米,则坡比是_______.
α
l
h
30
1:1
例:水库大坝的横断面是梯形,坝顶宽6m,坝高23m,斜坡AB的坡度i=1∶3,斜坡CD的坡度i=1∶2.5,求:
(1)坝底AD与斜坡AB的长度(精确到0.1m );
(2)斜坡CD的坡角α(精确到 1°).
E
F
A
D
B
C
i=1:2.5
23
6
α
分析:由坡度i会想到产生铅垂高度,即分别过点B、C 作AD的垂线;
垂线BE、CF将梯形分割成Rt△ABE,Rt△CFD和矩形BEFC,则AD=AE+EF+FD, EF=BC=6m,AE、DF可结合坡度,通过解Rt△ABE和Rt△CDF求出;
斜坡AB的长度以及斜坡CD的坡角的问题实质上就是解Rt△ ABE和Rt△ CDF.
解:(1)分别过点B、C作BE⊥AD,CF⊥AD,垂足分别为点E、 F,由题意可知
E
F
A
D
B
C
i=1:2.5
23
6
α
BE=CF=23m , EF=BC=6m.
在Rt△ABE中
在Rt△DCF中,同理可得
=69+6+57.5=132.5m.
在Rt△ABE中,由勾股定理可得
(2) 斜坡CD的坡度i=tanα=1:2.5=0.4,
由计算器可算得
答:坝底宽AD为132.5米,斜坡AB的长约为72.7米.斜坡CD的坡角α约为22°.
如图,拦水坝的横断面为梯形ABCD(图中i=1:3是指坡面的铅直高度DE与水平宽度CE的比),根据图中数据求:
(1)坡角a和β;
(2)坝顶宽AD和斜坡AB的长(精确到0.1m).
B
A
D
F
E
C
6m
α
β
i=1:3
i=1:1.5
解:(1)在Rt△AFB中,∠AFB=90°
在Rt△CDE中,∠CED=90°
完成第(2)题
1.如图(2),在高出海平面100米的悬崖顶A处,观测海平面上一艘小船B,并测得它的俯角为45°,则船与观测者之间的水平距离BC=_________米.
2.如图(3),两建筑物AB和CD的水平距离为30米,从A点测得D点的俯角为30°,测得C点的俯角为60°,则建筑物CD的高为_____米.
100
随堂练习
3.如图3,从地面上的C,D两点测得树顶A仰角分别是45°和30°,已知CD=200米,点C在BD上,则树高AB等于 (根号保留).
4.如图4,将宽为1cm的纸条沿BC折叠,使∠CAB=45°,则折叠后重叠部分的面积为 (根号保留).
图3
图4
5.一段路基的横断面是梯形,高为4米,上底的宽是12米,路基的坡面与地面的倾角分别是45°和30°,求路基下底的宽(精确到0.1米, ).
45°
30°
4米
12米
A
B
C
E
F
D
解:作DE⊥AB,CF⊥AB,垂足分别为E、F.由题意可知
DE=CF=4(米),
CD=EF=12(米).
在Rt△ADE中,
在Rt△BCF中,同理可得
因此AB=AE+EF+BF≈4+12+6.93≈22.93(米).
答: 路基下底的宽约为22.93米.
45°
30°
4米
12米
A
B
C
E
F
D
6.如下图,在一次数学课外活动中,测得电线杆底部B与钢缆固定点O的距离为4米,钢缆与地面的夹角∠BOA为60 ,则这条钢缆在电线杆上的固定点A到地面的距离AB是多少米(结果保留根号).
解:在Rt△ABO中,
∵tan∠BOA= =tan60°=
∴AB=BO tan60°=4 ×=4 (米)
答:这条钢缆在电线杆上的固定点A到地面的距离AB是4 米.
利用解直角三角形的知识解决实际问题的一般过程是:
(1)将实际问题抽象为数学问题(画出平面图形,转化为解直角三角形的问题);
(2)根据条件的特点,适当选用锐角三角函数等去解直角三角形;
(3)得到数学问题的答案;
(4)得到实际问题的答案.
课堂小结
同课章节目录
- 第23章 数据分析
- 23.1 平均数与加权平均数
- 23.2 中位数与众数
- 23.3 方差
- 23.4 用样本估计总体
- 第24章 一元二次方程
- 24.1 一元二次方程
- 24.2 解一元二次方程
- 24.3 一元二次方程根与系数的关系
- 24.4 一元二次方程的应用
- 第25章 图形的相似
- 25.1 比例线段
- 25.2 平行线分线段成比例
- 25.3 相似三角形
- 25.4 相似三角形的判定
- 25.5 相似三角形的性质
- 25.6 相似三角形的应用
- 25.7 相似多边形和图形的位似
- 第26章 解直角三角形
- 26.1 锐角三角函数
- 26.2 锐角三角函数的计算
- 26.3 解直角三角形
- 26.4 解直角三角形的应用
- 第27章 反比例函数
- 27.1 反比例函数
- 27.2 反比例函数的图像和性质
- 27.3 反比例函数的应用
- 第28章 圆
- 28.1 圆的概念和性质
- 28.2 过三点的圆
- 28.3 圆心角和圆周角
- 28.4 垂径定理
- 28.5 弧长和扇形面积
