山东省烟台招远市(五四制)2021-2022学年七年级上学期期中考试数学试卷(word版含答案)
文档属性
| 名称 | 山东省烟台招远市(五四制)2021-2022学年七年级上学期期中考试数学试卷(word版含答案) | 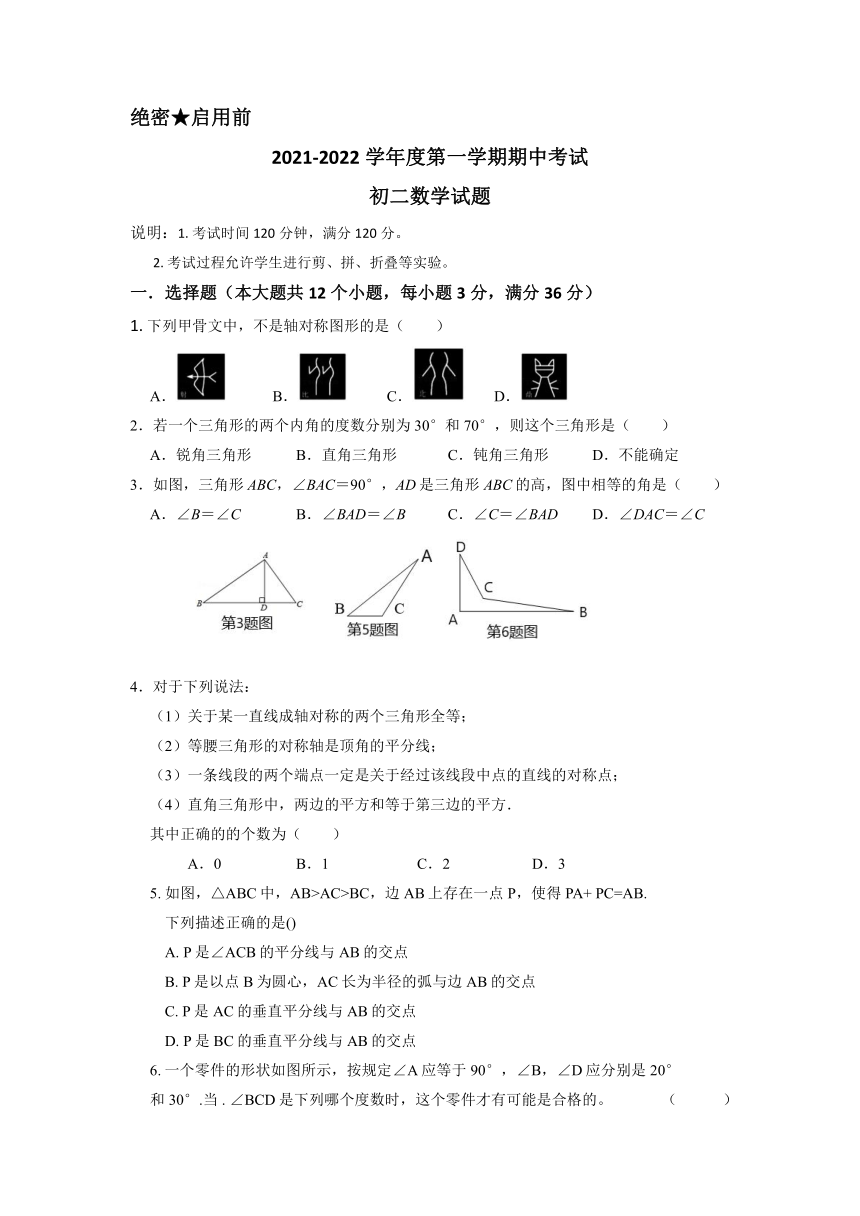 | |
| 格式 | docx | ||
| 文件大小 | 511.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-16 23:14:48 | ||
图片预览



文档简介
绝密★启用前
2021-2022学年度第一学期期中考试
初二数学试题
说明:1. 考试时间120分钟,满分120分。
2. 考试过程允许学生进行剪、拼、折叠等实验。
一.选择题(本大题共12个小题,每小题3分,满分36分)
1. 下列甲骨文中,不是轴对称图形的是( )
A. B. C. D.
2.若一个三角形的两个内角的度数分别为30°和70°,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
3.如图,三角形ABC,∠BAC=90°,AD是三角形ABC的高,图中相等的角是( )
A.∠B=∠C B.∠BAD=∠B C.∠C=∠BAD D.∠DAC=∠C
4.对于下列说法:
(1)关于某一直线成轴对称的两个三角形全等;
(2)等腰三角形的对称轴是顶角的平分线;
(3)一条线段的两个端点一定是关于经过该线段中点的直线的对称点;
(4)直角三角形中,两边的平方和等于第三边的平方.
其中正确的的个数为( )
A.0 B.1 C.2 D.3
5. 如图,△ABC中,AB>AC>BC,边AB上存在一点P,使得PA+ PC=AB.
下列描述正确的是()
P是∠ACB的平分线与AB的交点
P是以点B为圆心,AC长为半径的弧与边AB的交点
P是AC的垂直平分线与AB的交点
P是BC的垂直平分线与AB的交点
6. 一个零件的形状如图所示,按规定∠A应等于90°,∠B,∠D应分别是20°
和30°.当 . ∠BCD是下列哪个度数时,这个零件才有可能是合格的。 ( )
A.150° B.140° C.130 ° D.120°
7. 如图,在Rt△ABC中,∠C=90 ,AD平分∠BAC,交BC于点D,AB=10,
S△ABD=25,则CD的长为( )
A.2.5 B.4 C.5 D.10
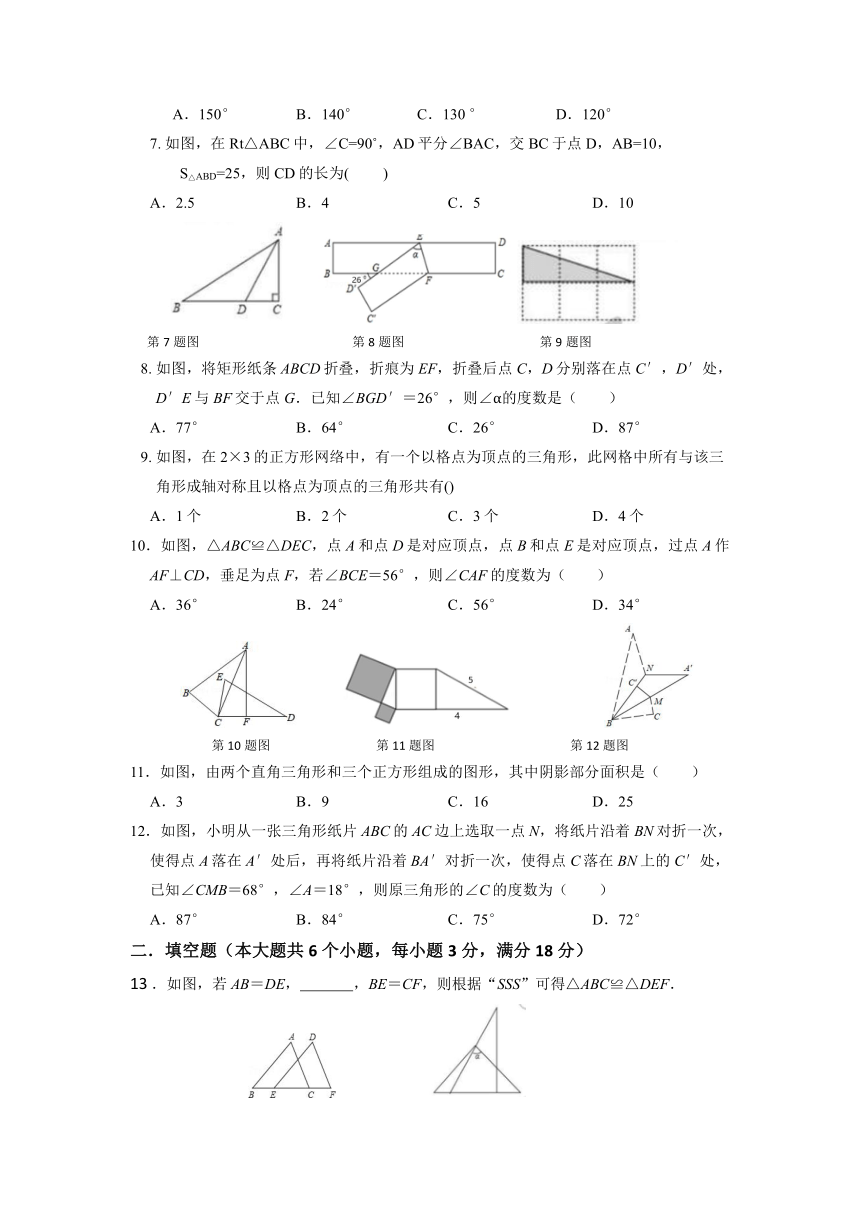
第7题图 第8题图 第9题图
如图,将矩形纸条ABCD折叠,折痕为EF,折叠后点C,D分别落在点C′,D′处,
D′E与BF交于点G.已知∠BGD′=26°,则∠α的度数是( )
A.77° B.64° C.26° D.87°
如图,在2×3的正方形网络中,有一个以格点为顶点的三角形,此网格中所有与该三
角形成轴对称且以格点为顶点的三角形共有()
A.1个 B.2个 C.3个 D.4个
10.如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=56°,则∠CAF的度数为( )
A.36° B.24° C.56° D.34°
第10题图 第11题图 第12题图
11.如图,由两个直角三角形和三个正方形组成的图形,其中阴影部分面积是( )
A.3 B.9 C.16 D.25
12.如图,小明从一张三角形纸片ABC的AC边上选取一点N,将纸片沿着BN对折一次,使得点A落在A′处后,再将纸片沿着BA′对折一次,使得点C落在BN上的C′处,已知∠CMB=68°,∠A=18°,则原三角形的∠C的度数为( )
A.87° B.84° C.75° D.72°
二.填空题(本大题共6个小题,每小题3分,满分18分)
13 .如图,若AB=DE, ,BE=CF,则根据“SSS”可得△ABC≌△DEF.
第13题图 第14题图
一副三角板如图叠放在一起,则图中α的度数为 .
15.已知等腰三角形腰长为5,一腰上的高为3,则以底边为边长的正方形的面积为 .
16. 如图,小明在计算机上用“几何画板”画了一个Rt△ABC,∠C=90 ,并画出了两锐角的角平分线AD, BE及其交点F..小明发现,无论怎祥变动Rt△ABC的形状和大小,∠AFB的度数是定值.这个定值为 .
17.如图,直线a过正方形ABCD的顶点A,点B、D到直线a的距离分别为5、12,则正方形的周长为 .
第16题图 第17题图 第18题图
18.如图,在△ABC中,AB=8,AC=11,AD⊥BC,垂足为D,M为AD上任一点,则MC2﹣MB2等于 .
三.解答题(本大题共7个小题,共66分.请在答题卡指定区域内作答.)
19.如图,在△ABC中,点P是AC上一点,连接BP,求作一点M,使得点M到AB和AC两边的距离相等,并且到点B和点P的距离相等.(不写作法,保留作图痕迹)
20. 在数学活动课上,王老师要求学生将图1所示的3×3正方形方格纸,涂黑其中三个方格,使剩下的部分成为轴对称图形.规定:凡通过旋转能重合的图形视为同一种图形,如图2的四幅图就视为同一种设计方案(阴影部分为涂黑部分)
请在图中画出4种不同的设计方案,将每种方案中三个方格涂黑(每个3×3的正方形方格画一种,例图除外,并且画上对称轴)
21.如图,AB=CB,AD=CD,AC,BD交于点O,OE⊥AB,OF⊥CB,垂足为E,F.说明OE=OF的理由.
第21题图 第22题图 第23题图
22.如图,一高层住宅发生火灾,消防车立即赶到距大厦9米处(车尾到大厦墙面),升起云梯到火灾窗口,已知云梯长15米,云梯底部距地面3米,问:发生火灾的住户窗口距离地面BD有多高?
23.如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD=BE.
(1)△ABD和△ECB全等吗?请说明理由
(2)若∠BDC=65°,求∠ADB的度数.
24.课本33页“想一想”,“如图,A,B两点分别位于一个池塘的两端,小明和小颖想用绳子测量A,B两点间的距离,他们想出了这样一个办法:先在地上取一个可以直接到达点A和点B的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度,DE 的长度就是A、B两点间的距离”
(1)你能说明其中的道理吗?
(2)你还有别的不同的方法吗?(可以使用直角工具)请写出具体方法,并说明理由。
图1 图2
25.如图,△BEF和△AGE是等腰直角三角形.
图3
(1)探究FG和AB的数量关系并说明理由;
(2)延长FG和AB交于点C,利用图2补全图形,求∠ACF的度数.
(3)当△BEF和△AGE如图3的位置时,请直接写出线段FG和AB的关系: .
2021—2022学年度第一学期期中考试
初二数学参考答案及评分意见
一.选择题(本大题共12个小题,每小题3分,满分36分)
1.B 2.A 3.C 4.B 5.D 6.B 7.C 8.A 9.C 10.D 11.B 12. B
二.填空题(本大题共6个小题,每小题3分,满分18分)
13.AC=DF 14.75° 15. 10或90 16.135° . 17.52 18.57
三.解答题(本大题共7个小题,共66分.请在答题卡指定区域内作答.)
19.解:
………………………………………………..5分
所以,点M就是所要求作的点 ………………………………………………..6分
20. 解:
………………………………………………..8分
21. 解:在△ABD和△CBD中,
由已知条件可知:AB=CB,AD=CD,
又因为BD是公共边 ,所以BD=BD
根据边边边定理可知,△ABD≌△CBD,………………………………………………..4分
因为全等三角形对应角相等,所以∠ABD=∠CBD,
即:BD是∠ABC的角平分线.
又因为OE⊥AB,OF⊥CB,
根据角平分线上的点到角两边的距离相等
所以OE=OF. ………………………………………………..8分
22. 解:过点A作AC⊥BD,垂足为C,
由题意可知: AE=CD=3,AC=9,AB=15;
在Rt△ABC中,根据勾股定理,得 ………………………………………………..3分
即,
BC=12 ………………………………………………..6分
∴BD=BC+CD=12+3=15;
答:发生火灾的住户窗口距离地面15米 ………………………………………………..8分
23. 解:(1)△ABD≌△ECB ………………………………………………..1分
理由:因为AD∥BC,
根据两直线平行,内错角相等可得:∠ADB=∠EBC,
又因为∠A=∠BEC,且AD=BE.
根据角边角定理,可得△ABD≌△ECB ………………………………………………..5分
(2)因为△ABD≌△ECB,
所以 BD=BC, ………………………………………………..7分
所以∠BDC=∠BCD=65°,
所以∠DBC=44°,
所以∠ADB=∠DBC=44°. …………………………..10分
24. 解:(1)在△ABC和△DEC中,
因为CA = CD,∠ACB= ∠DCE,CB = CE.
所以△ABC≌△DEC.
所以AB = DE.
即DE的长度就是A,B两点间的距离. ……..4分
(2)方法:在地面上取一个可以直接到达点A和点B的点C,连接AC,BC,使∠ACB=90°,然后在AC的延长线上确定点D,使CD=AC,连接BD并测量BD的长度,BD的长度就是A、B两点之间的距离。
………………………………………………..8分
理由:在△ABC和△DBC中,
因为CA = CD,∠ACB= ∠DCB,CB = CB.
所以△ABC≌△DBC.
AB=AD,
所以,通过测量BD的长可得AB的长.………………………………………………..12分
25.解:(1)FG=AB, ………………………………………………..1分
理由如下:
因为△BEF和△AGE是等腰直角三角形,
所以EF=EB,EA=EG,∠FEB=∠AEG=90°,
所以∠FEB﹣∠BEG=∠AEG﹣∠BEG,
即∠FEG=∠BEA,
在△FEG和△BEA中,
,
所以△FEG≌△BEA(SAS), ………………………………………………..5分
所以FG=AB; ………………………………………………..6分
(2)如图,即为补全的图形,
………………………………………………..7分
由(1)知△FEG≌△BEA,
所以∠EFG=∠EBA,
因为△BEF是等腰直角三角形,
所以∠EFB=∠EBF=45°,
所以∠CFB+∠CBF=∠CFB+∠EBF+∠CBE=∠EFB+∠EBF=90°,
所以∠FCB=108°-(∠CFB+∠CBF)=90°,
即CF⊥AB ………………………………………………..11分
(3)出线段FG和AB的关系:FG=AB且FG⊥AB …………………………………..14分
2021-2022学年度第一学期期中考试
初二数学试题
说明:1. 考试时间120分钟,满分120分。
2. 考试过程允许学生进行剪、拼、折叠等实验。
一.选择题(本大题共12个小题,每小题3分,满分36分)
1. 下列甲骨文中,不是轴对称图形的是( )
A. B. C. D.
2.若一个三角形的两个内角的度数分别为30°和70°,则这个三角形是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不能确定
3.如图,三角形ABC,∠BAC=90°,AD是三角形ABC的高,图中相等的角是( )
A.∠B=∠C B.∠BAD=∠B C.∠C=∠BAD D.∠DAC=∠C
4.对于下列说法:
(1)关于某一直线成轴对称的两个三角形全等;
(2)等腰三角形的对称轴是顶角的平分线;
(3)一条线段的两个端点一定是关于经过该线段中点的直线的对称点;
(4)直角三角形中,两边的平方和等于第三边的平方.
其中正确的的个数为( )
A.0 B.1 C.2 D.3
5. 如图,△ABC中,AB>AC>BC,边AB上存在一点P,使得PA+ PC=AB.
下列描述正确的是()
P是∠ACB的平分线与AB的交点
P是以点B为圆心,AC长为半径的弧与边AB的交点
P是AC的垂直平分线与AB的交点
P是BC的垂直平分线与AB的交点
6. 一个零件的形状如图所示,按规定∠A应等于90°,∠B,∠D应分别是20°
和30°.当 . ∠BCD是下列哪个度数时,这个零件才有可能是合格的。 ( )
A.150° B.140° C.130 ° D.120°
7. 如图,在Rt△ABC中,∠C=90 ,AD平分∠BAC,交BC于点D,AB=10,
S△ABD=25,则CD的长为( )
A.2.5 B.4 C.5 D.10
第7题图 第8题图 第9题图
如图,将矩形纸条ABCD折叠,折痕为EF,折叠后点C,D分别落在点C′,D′处,
D′E与BF交于点G.已知∠BGD′=26°,则∠α的度数是( )
A.77° B.64° C.26° D.87°
如图,在2×3的正方形网络中,有一个以格点为顶点的三角形,此网格中所有与该三
角形成轴对称且以格点为顶点的三角形共有()
A.1个 B.2个 C.3个 D.4个
10.如图,△ABC≌△DEC,点A和点D是对应顶点,点B和点E是对应顶点,过点A作AF⊥CD,垂足为点F,若∠BCE=56°,则∠CAF的度数为( )
A.36° B.24° C.56° D.34°
第10题图 第11题图 第12题图
11.如图,由两个直角三角形和三个正方形组成的图形,其中阴影部分面积是( )
A.3 B.9 C.16 D.25
12.如图,小明从一张三角形纸片ABC的AC边上选取一点N,将纸片沿着BN对折一次,使得点A落在A′处后,再将纸片沿着BA′对折一次,使得点C落在BN上的C′处,已知∠CMB=68°,∠A=18°,则原三角形的∠C的度数为( )
A.87° B.84° C.75° D.72°
二.填空题(本大题共6个小题,每小题3分,满分18分)
13 .如图,若AB=DE, ,BE=CF,则根据“SSS”可得△ABC≌△DEF.
第13题图 第14题图
一副三角板如图叠放在一起,则图中α的度数为 .
15.已知等腰三角形腰长为5,一腰上的高为3,则以底边为边长的正方形的面积为 .
16. 如图,小明在计算机上用“几何画板”画了一个Rt△ABC,∠C=90 ,并画出了两锐角的角平分线AD, BE及其交点F..小明发现,无论怎祥变动Rt△ABC的形状和大小,∠AFB的度数是定值.这个定值为 .
17.如图,直线a过正方形ABCD的顶点A,点B、D到直线a的距离分别为5、12,则正方形的周长为 .
第16题图 第17题图 第18题图
18.如图,在△ABC中,AB=8,AC=11,AD⊥BC,垂足为D,M为AD上任一点,则MC2﹣MB2等于 .
三.解答题(本大题共7个小题,共66分.请在答题卡指定区域内作答.)
19.如图,在△ABC中,点P是AC上一点,连接BP,求作一点M,使得点M到AB和AC两边的距离相等,并且到点B和点P的距离相等.(不写作法,保留作图痕迹)
20. 在数学活动课上,王老师要求学生将图1所示的3×3正方形方格纸,涂黑其中三个方格,使剩下的部分成为轴对称图形.规定:凡通过旋转能重合的图形视为同一种图形,如图2的四幅图就视为同一种设计方案(阴影部分为涂黑部分)
请在图中画出4种不同的设计方案,将每种方案中三个方格涂黑(每个3×3的正方形方格画一种,例图除外,并且画上对称轴)
21.如图,AB=CB,AD=CD,AC,BD交于点O,OE⊥AB,OF⊥CB,垂足为E,F.说明OE=OF的理由.
第21题图 第22题图 第23题图
22.如图,一高层住宅发生火灾,消防车立即赶到距大厦9米处(车尾到大厦墙面),升起云梯到火灾窗口,已知云梯长15米,云梯底部距地面3米,问:发生火灾的住户窗口距离地面BD有多高?
23.如图,在四边形ABCD中,AD∥BC,点E为对角线BD上一点,∠A=∠BEC,且AD=BE.
(1)△ABD和△ECB全等吗?请说明理由
(2)若∠BDC=65°,求∠ADB的度数.
24.课本33页“想一想”,“如图,A,B两点分别位于一个池塘的两端,小明和小颖想用绳子测量A,B两点间的距离,他们想出了这样一个办法:先在地上取一个可以直接到达点A和点B的点C,连接AC并延长到D,使CD=CA;连接BC并延长到E,使CE=CB;连接DE并测量出它的长度,DE 的长度就是A、B两点间的距离”
(1)你能说明其中的道理吗?
(2)你还有别的不同的方法吗?(可以使用直角工具)请写出具体方法,并说明理由。
图1 图2
25.如图,△BEF和△AGE是等腰直角三角形.
图3
(1)探究FG和AB的数量关系并说明理由;
(2)延长FG和AB交于点C,利用图2补全图形,求∠ACF的度数.
(3)当△BEF和△AGE如图3的位置时,请直接写出线段FG和AB的关系: .
2021—2022学年度第一学期期中考试
初二数学参考答案及评分意见
一.选择题(本大题共12个小题,每小题3分,满分36分)
1.B 2.A 3.C 4.B 5.D 6.B 7.C 8.A 9.C 10.D 11.B 12. B
二.填空题(本大题共6个小题,每小题3分,满分18分)
13.AC=DF 14.75° 15. 10或90 16.135° . 17.52 18.57
三.解答题(本大题共7个小题,共66分.请在答题卡指定区域内作答.)
19.解:
………………………………………………..5分
所以,点M就是所要求作的点 ………………………………………………..6分
20. 解:
………………………………………………..8分
21. 解:在△ABD和△CBD中,
由已知条件可知:AB=CB,AD=CD,
又因为BD是公共边 ,所以BD=BD
根据边边边定理可知,△ABD≌△CBD,………………………………………………..4分
因为全等三角形对应角相等,所以∠ABD=∠CBD,
即:BD是∠ABC的角平分线.
又因为OE⊥AB,OF⊥CB,
根据角平分线上的点到角两边的距离相等
所以OE=OF. ………………………………………………..8分
22. 解:过点A作AC⊥BD,垂足为C,
由题意可知: AE=CD=3,AC=9,AB=15;
在Rt△ABC中,根据勾股定理,得 ………………………………………………..3分
即,
BC=12 ………………………………………………..6分
∴BD=BC+CD=12+3=15;
答:发生火灾的住户窗口距离地面15米 ………………………………………………..8分
23. 解:(1)△ABD≌△ECB ………………………………………………..1分
理由:因为AD∥BC,
根据两直线平行,内错角相等可得:∠ADB=∠EBC,
又因为∠A=∠BEC,且AD=BE.
根据角边角定理,可得△ABD≌△ECB ………………………………………………..5分
(2)因为△ABD≌△ECB,
所以 BD=BC, ………………………………………………..7分
所以∠BDC=∠BCD=65°,
所以∠DBC=44°,
所以∠ADB=∠DBC=44°. …………………………..10分
24. 解:(1)在△ABC和△DEC中,
因为CA = CD,∠ACB= ∠DCE,CB = CE.
所以△ABC≌△DEC.
所以AB = DE.
即DE的长度就是A,B两点间的距离. ……..4分
(2)方法:在地面上取一个可以直接到达点A和点B的点C,连接AC,BC,使∠ACB=90°,然后在AC的延长线上确定点D,使CD=AC,连接BD并测量BD的长度,BD的长度就是A、B两点之间的距离。
………………………………………………..8分
理由:在△ABC和△DBC中,
因为CA = CD,∠ACB= ∠DCB,CB = CB.
所以△ABC≌△DBC.
AB=AD,
所以,通过测量BD的长可得AB的长.………………………………………………..12分
25.解:(1)FG=AB, ………………………………………………..1分
理由如下:
因为△BEF和△AGE是等腰直角三角形,
所以EF=EB,EA=EG,∠FEB=∠AEG=90°,
所以∠FEB﹣∠BEG=∠AEG﹣∠BEG,
即∠FEG=∠BEA,
在△FEG和△BEA中,
,
所以△FEG≌△BEA(SAS), ………………………………………………..5分
所以FG=AB; ………………………………………………..6分
(2)如图,即为补全的图形,
………………………………………………..7分
由(1)知△FEG≌△BEA,
所以∠EFG=∠EBA,
因为△BEF是等腰直角三角形,
所以∠EFB=∠EBF=45°,
所以∠CFB+∠CBF=∠CFB+∠EBF+∠CBE=∠EFB+∠EBF=90°,
所以∠FCB=108°-(∠CFB+∠CBF)=90°,
即CF⊥AB ………………………………………………..11分
(3)出线段FG和AB的关系:FG=AB且FG⊥AB …………………………………..14分
同课章节目录
