陕西省宁强县天津高级中学高一物理《探究弹力与弹簧伸长的关系》课件
文档属性
| 名称 | 陕西省宁强县天津高级中学高一物理《探究弹力与弹簧伸长的关系》课件 |
|
|
| 格式 | zip | ||
| 文件大小 | 401.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 物理 | ||
| 更新时间 | 2012-09-25 00:00:00 | ||
图片预览





文档简介
(共16张PPT)
二、实验原理
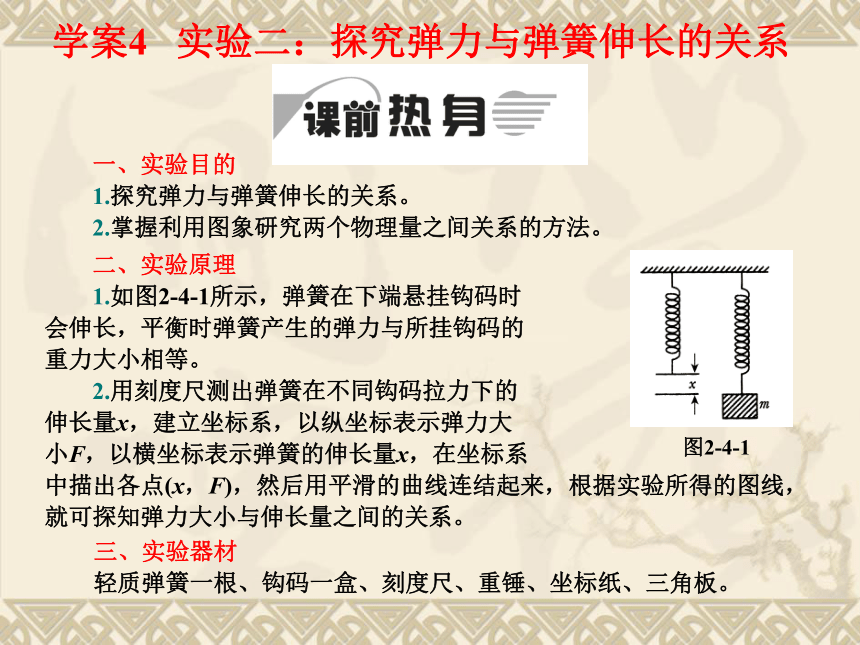
1.如图2-4-1所示,弹簧在下端悬挂钩码时
会伸长,平衡时弹簧产生的弹力与所挂钩码的
重力大小相等。
2.用刻度尺测出弹簧在不同钩码拉力下的
伸长量x,建立坐标系,以纵坐标表示弹力大
小F,以横坐标表示弹簧的伸长量x,在坐标系
中描出各点(x,F),然后用平滑的曲线连结起来,根据实验所得的图线,就可探知弹力大小与伸长量之间的关系。
图2-4-1
三、实验器材
轻质弹簧一根、钩码一盒、刻度尺、重锤、坐标纸、三角板。
一、实验目的
1.探究弹力与弹簧伸长的关系。
2.掌握利用图象研究两个物理量之间关系的方法。
学案4 实验二:探究弹力与弹簧伸长的关系
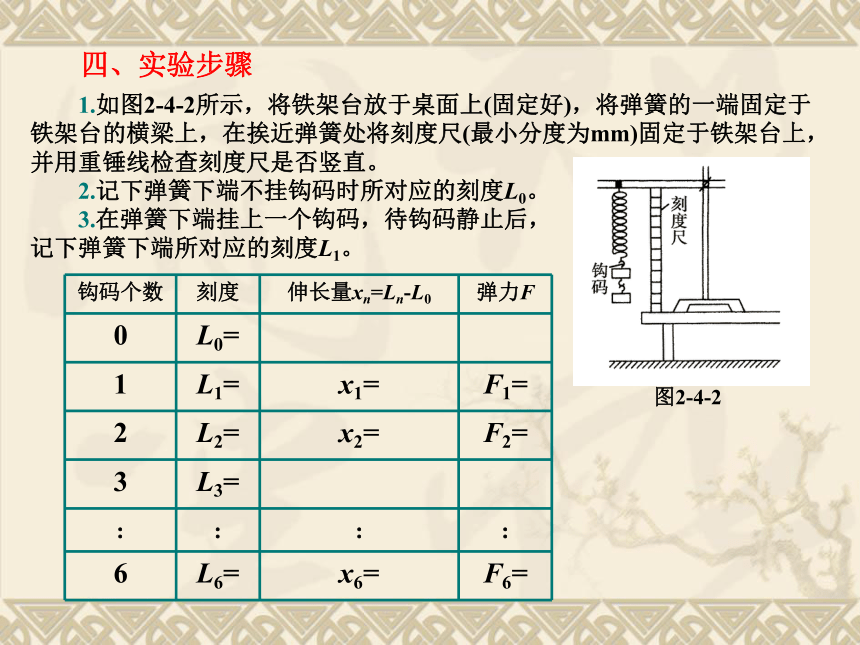
1.如图2-4-2所示,将铁架台放于桌面上(固定好),将弹簧的一端固定于铁架台的横梁上,在挨近弹簧处将刻度尺(最小分度为mm)固定于铁架台上,并用重锤线检查刻度尺是否竖直。
2.记下弹簧下端不挂钩码时所对应的刻度L0。
3.在弹簧下端挂上一个钩码,待钩码静止后,
记下弹簧下端所对应的刻度L1。
图2-4-2
钩码个数 刻度 伸长量xn=Ln-L0 弹力F
0 L0=
1 L1= x1= F1=
2 L2= x2= F2=
3 L3=
﹕ ﹕ ﹕ ﹕
6 L6= x6= F6=
四、实验步骤
4.用上面方法,记下弹簧下端挂2个、3个、4个…钩码时,弹簧下端所对应的刻度L2、L3、L4…,并将所得数据记录在表格中。
5.用xn=Ln-L0计算出弹簧挂1个、2个、3个…钩码时弹簧的伸长量,并根据当地重力加速度值g,计算出所挂钩码的总重量,这个总重量就是弹簧弹力的大小,将所得数据填入表格。
6.在坐标纸上建立坐标系,以弹力为纵坐标,弹簧伸长量为横坐标,描出每一组数据(x,F)所对应的点。
7.根据所描各点的分布与走向,作出一条平滑的曲线(不能画成折线)。
8.以弹簧伸长量为自变量,弹力大小为因变量,写出曲线所代表的函数。首先尝试写成一次函数的形式,如果不行,写成二次函数的形式或其他形式。
9.研究并解释函数表达式中常数的物理意义。
五、注意事项
1.安装时,要保持刻度尺竖直并靠近弹簧。
2.实验时,要尽量选择长度较大、匝数较多,但软硬程度(劲度系数)适中的弹簧,以每挂一个钩码(20 g)弹簧伸长量增大1~2 cm为宜。
3.读取弹簧下端所对应的刻度时,要用三角板,并且视线垂直于刻度,力求读数准确,并且要等钩码静止时,再读数。
4.实验中悬挂钩码时注意不要太多,以免弹簧被过分拉伸,超过弹簧的弹性限度。
5.要使用轻质弹簧,且要尽量多测几组数据。
6.建立坐标系时,要选择合适标度,以使所画曲线占据整个坐标纸。
7.画图线时,不一定要让所有各点都正好在曲线上,但应注意使曲线两侧的点大致相同,偏离太远的点要舍弃。
在物理学中经常用图象处理物理问
题,要特别注意:①图线斜率的意
义(或曲线切线斜率的意义);②图线与纵轴横轴交点的物理意义。
六、误差分析
本实验的误差主要来自以下两个方面:
1.弹簧的长度测量不精确。
2.描点、画图不精确。
本题主要考查使用弹簧时应注意的问题,还有用图象法来描述弹簧的弹力与其伸长量间的关系。
(1)实验中应以所研究的一根弹簧为实验对象,在弹性限度内通过增减钩码的数目来改变对弹簧的拉力,以探究弹力与弹簧伸长的关系,并且拉力和重力平衡,所以选A、B。
(2)由于考虑弹簧自身重力的影响,当不挂钩码时,弹簧的伸长量x 0,所以选C。
【例1】(1)在“探究弹力与弹簧伸长的关系”的实验中,以下说法正确的是 ( )
A.弹簧被拉伸时,不能超出它的弹性限度
B.用悬挂钩码的方法给弹簧施加拉力,应保证弹簧位于竖直位置且处于平衡状态
C.用直尺测得弹簧的长度即为弹簧的伸长量
D.用几个不同的弹簧,分别测出几组拉力与伸长量,得出拉力与伸长量之比相等
(2)某同学做“探究弹力与弹簧伸长的关系”的实验,他先把弹簧平放在桌面上使其
自然伸长,用直尺测出弹簧的原长L0,再把弹簧竖直悬挂起来,挂上钩码后测
出弹簧伸长后的长度L,把L-L0作为弹簧的伸长量x,这样操作,由于弹簧的自
身重力的影响,最后画出的图线可能是图中的 ( )
AB
C
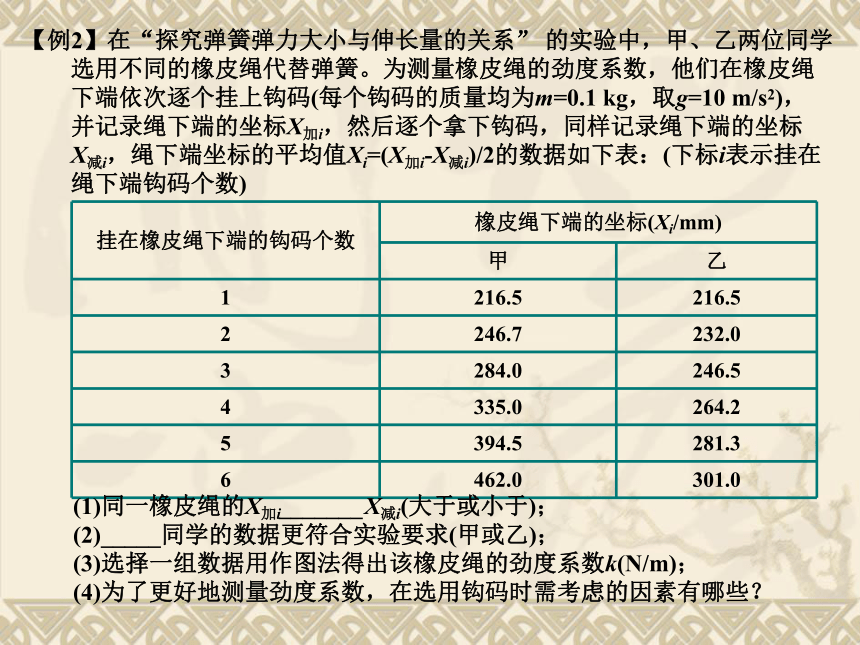
【例2】在“探究弹簧弹力大小与伸长量的关系” 的实验中,甲、乙两位同学
选用不同的橡皮绳代替弹簧。为测量橡皮绳的劲度系数,他们在橡皮绳
下端依次逐个挂上钩码(每个钩码的质量均为m=0.1 kg,取g=10 m/s2),
并记录绳下端的坐标X加i,然后逐个拿下钩码,同样记录绳下端的坐标
X减i,绳下端坐标的平均值Xi=(X加i-X减i)/2的数据如下表:(下标i表示挂在
绳下端钩码个数)
挂在橡皮绳下端的钩码个数 橡皮绳下端的坐标(Xi/mm)
甲 乙
1 216.5 216.5
2 246.7 232.0
3 284.0 246.5
4 335.0 264.2
5 394.5 281.3
6 462.0 301.0
(1)同一橡皮绳的X加i_______X减i(大于或小于);
(2)_____同学的数据更符合实验要求(甲或乙);
(3)选择一组数据用作图法得出该橡皮绳的劲度系数k(N/m);
(4)为了更好地测量劲度系数,在选用钩码时需考虑的因素有哪些?
(1)小于 (2)乙 (3)63 N/m (4)见解析
(1)由甲、乙两同学测量数据看,橡皮绳所受拉力接近或超过了其弹性限度,其恢复能力要差一些,而且拉伸越长恢复能力越差。故X加i小于X减i。
(2)乙同学的数据更符合实验要求,每增加一个钩码橡皮绳形变量大致相同,而甲同学所用橡皮绳的形变量差别非常大,表明已超过了弹性限度。
(3)以乙同学数据作图象如图所示。
(4)尽可能使橡皮绳伸长量在弹性
限度内,同时有足够大的伸长量,以
减小长度测量误差。
1.做“探究弹力与弹簧伸长的关系”的实验步骤如下:
A.以弹簧伸长量为横坐标,以弹力大小为纵坐标,描出各组数据(x,F)对
应的点,并用平滑的曲线连结起来;
B.记下弹簧不挂钩码时,其下端在刻度尺上的刻度L0;
C.将铁架台固定于桌子上(也可在横梁的另一侧挂上一定的配重),并将弹
簧的一端系于横梁上,在弹簧附近竖直固定一刻度尺;
D.依次在弹簧下端挂上2个、3个、4个…钩码,并分别记下钩码静止时,
弹簧下端所对应的刻度并记录在表格内,然后取下钩码;
E.以弹簧伸长量x为自变量,写出弹力大小F与伸长量x的关系式。首先尝
试写成一次函数,如果不行,再尝试着写成二次函数;
F.解释函数表达式中常数的物理意义;
G.整理仪器。
请将以上步骤按操作的先后顺序排列起来:___________________。
C B D A E F G
(1)根据所测数据,在如图2-4-4所示的坐标纸上作出弹簧指针所指的标尺刻度x与钩码质量m的关系曲线。
(2)根据所测得的数据和关系曲线可以判断,在____N范围内弹力大小与弹簧伸长量关系满足胡克定律,这种规律的弹簧的劲度系数为____N/m。
2.某同学用如图2-4-3所示的装置做的探究弹力和弹簧伸长量关系的实验。他
先测出不挂钩码时弹簧下端指针所指的标尺刻度,然后在弹簧下端挂上钩
码,并逐个增加钩码,测出指针所指的标尺刻度,所得数据列表如下:(重
力加速度取g=9.8 m/s2)
4.9
图2-4-4
图2-4-3
钩码质量
m/102g 0 1.00 2.00 3.00 4.00 5.00 6.00 7.00
标尺刻度
x/10-2m 15.00 18.94 22.82 26.78 30.66 34.60 42.00 54.50
25
(1)根据题目所测量的数据进行描点,然后用平滑的曲线(或直线)连接各点,在连接时让尽量多的点落在线上(偏差比较大的点舍去),不在线上的点尽量平均分配在线的两侧,如图所示。
2.如图2-4-5所示,一个弹簧一端固定在传感器上,传感器与电脑相连。当对弹簧
施加变化的作用力(拉力或压力)时,在电脑上得到了弹簧形变量与弹簧产生弹力
大小的关系图象(如图乙),则下列判断正确的是 ( )
A.弹簧产生的弹力和弹簧的长度成正比
B.弹簧长度的增加量与对应的弹力增加量成正比
C.该弹簧的劲度系数是200 N/m
D.该弹簧受到反向压力时,劲度系数不变
1.在“探究弹力与弹簧伸长的关系”的实验中关于操作步骤的先后顺序,下列说法
中正确的是 ( )
A.先测量原长,后竖直悬挂
B.先竖直悬挂,后测量原长
C.先后顺序对实验结果无影响
D.先后顺序对实验结果的影响程度取决于弹簧的自重
B D
B C D
图2-4-5
3.某实验小组研究橡皮筋伸长与所受拉力的关系。实验时,将
原长约200 mm的橡皮筋上端固定,在竖直悬挂的橡皮筋下端
逐一增挂钩码(质量均为20 g),每增挂一只钩码均记下对应的
橡皮筋伸长量;当挂上10只钩码后,再逐一把钩码取下,每
取下一只钩码,也记下对应的橡皮筋伸
长量。根据测量数据,作出增挂钩码和
减挂钩码时的橡皮筋伸长量 l与拉力F
关系的图象如图2-4-6所示。从图象中可
以得出_____。(填选项前的字母)
A.增挂钩码时 l与F成正比,而减挂钩码时 l与F不成正比
B.当所挂钩码数相同时,增挂钩码时橡皮筋的伸长量比减
挂钩码时的大
C.当所挂钩码数相同时,增挂钩码时橡皮筋的伸长量与减
挂钩码时的相等
D.增挂钩码时所挂钩码数过多,导致橡皮筋超出弹性限度
D
图2-4-6
4.下表是一位同学探究弹力大小与弹簧伸长量之间的关系所
测的几组数据:
图2-4-7
①在如图2-4-7所示的坐标上作出F-x图线。
②写出曲线的函数表达式(x用cm作单位):
_________________。
③函数表达式中常数的物理意义:。
弹力(F/N) 0.5 1.0 1.5 2.0 2.5
弹簧原来长度(L0/cm) 15 15 15 15 15
弹簧后来长度(L/cm) 16.2 17.3 18.5 19.6 20.8
弹簧伸长量(x/cm) 1.2 2.3 3.5 4.6 5.8
弹簧的劲度系数
F=0.43x
5.如图2-4-8所示,某同学和你一起探究弹力与弹簧伸
长的关系,并测弹簧的劲度系数k。做法是先将待测
弹簧的一端固定在铁架台上,然后将最小刻度是毫
米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的
指针恰好落在刻度尺上。当弹簧自然下垂时,指针
指示的刻度值记作L0;弹簧下端挂一个50 g的砝码时,
指针指示的刻度数值记作L1;弹簧下端挂两个50 g的
砝码时,指针指示的刻度数值记作L2;……挂七个50 g的砝码时,指针指示
的刻度数值记作L7。
(1)下表记录的是该同学已测出的6个值,其中有两个数值在记录时有误,它
们的代表符号分别是_____和______。
(2)测量记录表:
图2-4-8
代表符号 L0 L1 L2 L3 L4 L5 L6 L7
刻度数值/ cm 1.70 3.40 5.10 8.60 10.3 12.1
实验中,L3和L7两个值还没有测定,请你根据上图将这两个测量值填入记录表中。
(3)为充分利用测量数据,该同学将所测得的数值按如下方
法逐一求差,分别计算出了三个差值:d1=L4-L0=6.90 cm,
d2=L5-L1=6.90 cm,d3=L6-L2=7.00 cm。
请你给出第四个差值:d4=______=______ cm。
(4)根据以上差值,可以求出每增加50 g砝码的弹簧平均伸长
量 L。 L用d1、d2、d3、d4表示的式子为: L=________。
代入数据解得 L=_____ cm。
(5)计算弹簧的劲度系数k=______ N/m。(取g=9.8 m/s2)
(1)L5 L6
(2)6.85(6.84~6.86) 14.05(14.04~14.06)
(3)L7-L3 7.20(7.18~7.22)
(4)(d1+d2+d3+d4)/(4×4) 1.75
(5)28
二、实验原理
1.如图2-4-1所示,弹簧在下端悬挂钩码时
会伸长,平衡时弹簧产生的弹力与所挂钩码的
重力大小相等。
2.用刻度尺测出弹簧在不同钩码拉力下的
伸长量x,建立坐标系,以纵坐标表示弹力大
小F,以横坐标表示弹簧的伸长量x,在坐标系
中描出各点(x,F),然后用平滑的曲线连结起来,根据实验所得的图线,就可探知弹力大小与伸长量之间的关系。
图2-4-1
三、实验器材
轻质弹簧一根、钩码一盒、刻度尺、重锤、坐标纸、三角板。
一、实验目的
1.探究弹力与弹簧伸长的关系。
2.掌握利用图象研究两个物理量之间关系的方法。
学案4 实验二:探究弹力与弹簧伸长的关系
1.如图2-4-2所示,将铁架台放于桌面上(固定好),将弹簧的一端固定于铁架台的横梁上,在挨近弹簧处将刻度尺(最小分度为mm)固定于铁架台上,并用重锤线检查刻度尺是否竖直。
2.记下弹簧下端不挂钩码时所对应的刻度L0。
3.在弹簧下端挂上一个钩码,待钩码静止后,
记下弹簧下端所对应的刻度L1。
图2-4-2
钩码个数 刻度 伸长量xn=Ln-L0 弹力F
0 L0=
1 L1= x1= F1=
2 L2= x2= F2=
3 L3=
﹕ ﹕ ﹕ ﹕
6 L6= x6= F6=
四、实验步骤
4.用上面方法,记下弹簧下端挂2个、3个、4个…钩码时,弹簧下端所对应的刻度L2、L3、L4…,并将所得数据记录在表格中。
5.用xn=Ln-L0计算出弹簧挂1个、2个、3个…钩码时弹簧的伸长量,并根据当地重力加速度值g,计算出所挂钩码的总重量,这个总重量就是弹簧弹力的大小,将所得数据填入表格。
6.在坐标纸上建立坐标系,以弹力为纵坐标,弹簧伸长量为横坐标,描出每一组数据(x,F)所对应的点。
7.根据所描各点的分布与走向,作出一条平滑的曲线(不能画成折线)。
8.以弹簧伸长量为自变量,弹力大小为因变量,写出曲线所代表的函数。首先尝试写成一次函数的形式,如果不行,写成二次函数的形式或其他形式。
9.研究并解释函数表达式中常数的物理意义。
五、注意事项
1.安装时,要保持刻度尺竖直并靠近弹簧。
2.实验时,要尽量选择长度较大、匝数较多,但软硬程度(劲度系数)适中的弹簧,以每挂一个钩码(20 g)弹簧伸长量增大1~2 cm为宜。
3.读取弹簧下端所对应的刻度时,要用三角板,并且视线垂直于刻度,力求读数准确,并且要等钩码静止时,再读数。
4.实验中悬挂钩码时注意不要太多,以免弹簧被过分拉伸,超过弹簧的弹性限度。
5.要使用轻质弹簧,且要尽量多测几组数据。
6.建立坐标系时,要选择合适标度,以使所画曲线占据整个坐标纸。
7.画图线时,不一定要让所有各点都正好在曲线上,但应注意使曲线两侧的点大致相同,偏离太远的点要舍弃。
在物理学中经常用图象处理物理问
题,要特别注意:①图线斜率的意
义(或曲线切线斜率的意义);②图线与纵轴横轴交点的物理意义。
六、误差分析
本实验的误差主要来自以下两个方面:
1.弹簧的长度测量不精确。
2.描点、画图不精确。
本题主要考查使用弹簧时应注意的问题,还有用图象法来描述弹簧的弹力与其伸长量间的关系。
(1)实验中应以所研究的一根弹簧为实验对象,在弹性限度内通过增减钩码的数目来改变对弹簧的拉力,以探究弹力与弹簧伸长的关系,并且拉力和重力平衡,所以选A、B。
(2)由于考虑弹簧自身重力的影响,当不挂钩码时,弹簧的伸长量x 0,所以选C。
【例1】(1)在“探究弹力与弹簧伸长的关系”的实验中,以下说法正确的是 ( )
A.弹簧被拉伸时,不能超出它的弹性限度
B.用悬挂钩码的方法给弹簧施加拉力,应保证弹簧位于竖直位置且处于平衡状态
C.用直尺测得弹簧的长度即为弹簧的伸长量
D.用几个不同的弹簧,分别测出几组拉力与伸长量,得出拉力与伸长量之比相等
(2)某同学做“探究弹力与弹簧伸长的关系”的实验,他先把弹簧平放在桌面上使其
自然伸长,用直尺测出弹簧的原长L0,再把弹簧竖直悬挂起来,挂上钩码后测
出弹簧伸长后的长度L,把L-L0作为弹簧的伸长量x,这样操作,由于弹簧的自
身重力的影响,最后画出的图线可能是图中的 ( )
AB
C
【例2】在“探究弹簧弹力大小与伸长量的关系” 的实验中,甲、乙两位同学
选用不同的橡皮绳代替弹簧。为测量橡皮绳的劲度系数,他们在橡皮绳
下端依次逐个挂上钩码(每个钩码的质量均为m=0.1 kg,取g=10 m/s2),
并记录绳下端的坐标X加i,然后逐个拿下钩码,同样记录绳下端的坐标
X减i,绳下端坐标的平均值Xi=(X加i-X减i)/2的数据如下表:(下标i表示挂在
绳下端钩码个数)
挂在橡皮绳下端的钩码个数 橡皮绳下端的坐标(Xi/mm)
甲 乙
1 216.5 216.5
2 246.7 232.0
3 284.0 246.5
4 335.0 264.2
5 394.5 281.3
6 462.0 301.0
(1)同一橡皮绳的X加i_______X减i(大于或小于);
(2)_____同学的数据更符合实验要求(甲或乙);
(3)选择一组数据用作图法得出该橡皮绳的劲度系数k(N/m);
(4)为了更好地测量劲度系数,在选用钩码时需考虑的因素有哪些?
(1)小于 (2)乙 (3)63 N/m (4)见解析
(1)由甲、乙两同学测量数据看,橡皮绳所受拉力接近或超过了其弹性限度,其恢复能力要差一些,而且拉伸越长恢复能力越差。故X加i小于X减i。
(2)乙同学的数据更符合实验要求,每增加一个钩码橡皮绳形变量大致相同,而甲同学所用橡皮绳的形变量差别非常大,表明已超过了弹性限度。
(3)以乙同学数据作图象如图所示。
(4)尽可能使橡皮绳伸长量在弹性
限度内,同时有足够大的伸长量,以
减小长度测量误差。
1.做“探究弹力与弹簧伸长的关系”的实验步骤如下:
A.以弹簧伸长量为横坐标,以弹力大小为纵坐标,描出各组数据(x,F)对
应的点,并用平滑的曲线连结起来;
B.记下弹簧不挂钩码时,其下端在刻度尺上的刻度L0;
C.将铁架台固定于桌子上(也可在横梁的另一侧挂上一定的配重),并将弹
簧的一端系于横梁上,在弹簧附近竖直固定一刻度尺;
D.依次在弹簧下端挂上2个、3个、4个…钩码,并分别记下钩码静止时,
弹簧下端所对应的刻度并记录在表格内,然后取下钩码;
E.以弹簧伸长量x为自变量,写出弹力大小F与伸长量x的关系式。首先尝
试写成一次函数,如果不行,再尝试着写成二次函数;
F.解释函数表达式中常数的物理意义;
G.整理仪器。
请将以上步骤按操作的先后顺序排列起来:___________________。
C B D A E F G
(1)根据所测数据,在如图2-4-4所示的坐标纸上作出弹簧指针所指的标尺刻度x与钩码质量m的关系曲线。
(2)根据所测得的数据和关系曲线可以判断,在____N范围内弹力大小与弹簧伸长量关系满足胡克定律,这种规律的弹簧的劲度系数为____N/m。
2.某同学用如图2-4-3所示的装置做的探究弹力和弹簧伸长量关系的实验。他
先测出不挂钩码时弹簧下端指针所指的标尺刻度,然后在弹簧下端挂上钩
码,并逐个增加钩码,测出指针所指的标尺刻度,所得数据列表如下:(重
力加速度取g=9.8 m/s2)
4.9
图2-4-4
图2-4-3
钩码质量
m/102g 0 1.00 2.00 3.00 4.00 5.00 6.00 7.00
标尺刻度
x/10-2m 15.00 18.94 22.82 26.78 30.66 34.60 42.00 54.50
25
(1)根据题目所测量的数据进行描点,然后用平滑的曲线(或直线)连接各点,在连接时让尽量多的点落在线上(偏差比较大的点舍去),不在线上的点尽量平均分配在线的两侧,如图所示。
2.如图2-4-5所示,一个弹簧一端固定在传感器上,传感器与电脑相连。当对弹簧
施加变化的作用力(拉力或压力)时,在电脑上得到了弹簧形变量与弹簧产生弹力
大小的关系图象(如图乙),则下列判断正确的是 ( )
A.弹簧产生的弹力和弹簧的长度成正比
B.弹簧长度的增加量与对应的弹力增加量成正比
C.该弹簧的劲度系数是200 N/m
D.该弹簧受到反向压力时,劲度系数不变
1.在“探究弹力与弹簧伸长的关系”的实验中关于操作步骤的先后顺序,下列说法
中正确的是 ( )
A.先测量原长,后竖直悬挂
B.先竖直悬挂,后测量原长
C.先后顺序对实验结果无影响
D.先后顺序对实验结果的影响程度取决于弹簧的自重
B D
B C D
图2-4-5
3.某实验小组研究橡皮筋伸长与所受拉力的关系。实验时,将
原长约200 mm的橡皮筋上端固定,在竖直悬挂的橡皮筋下端
逐一增挂钩码(质量均为20 g),每增挂一只钩码均记下对应的
橡皮筋伸长量;当挂上10只钩码后,再逐一把钩码取下,每
取下一只钩码,也记下对应的橡皮筋伸
长量。根据测量数据,作出增挂钩码和
减挂钩码时的橡皮筋伸长量 l与拉力F
关系的图象如图2-4-6所示。从图象中可
以得出_____。(填选项前的字母)
A.增挂钩码时 l与F成正比,而减挂钩码时 l与F不成正比
B.当所挂钩码数相同时,增挂钩码时橡皮筋的伸长量比减
挂钩码时的大
C.当所挂钩码数相同时,增挂钩码时橡皮筋的伸长量与减
挂钩码时的相等
D.增挂钩码时所挂钩码数过多,导致橡皮筋超出弹性限度
D
图2-4-6
4.下表是一位同学探究弹力大小与弹簧伸长量之间的关系所
测的几组数据:
图2-4-7
①在如图2-4-7所示的坐标上作出F-x图线。
②写出曲线的函数表达式(x用cm作单位):
_________________。
③函数表达式中常数的物理意义:。
弹力(F/N) 0.5 1.0 1.5 2.0 2.5
弹簧原来长度(L0/cm) 15 15 15 15 15
弹簧后来长度(L/cm) 16.2 17.3 18.5 19.6 20.8
弹簧伸长量(x/cm) 1.2 2.3 3.5 4.6 5.8
弹簧的劲度系数
F=0.43x
5.如图2-4-8所示,某同学和你一起探究弹力与弹簧伸
长的关系,并测弹簧的劲度系数k。做法是先将待测
弹簧的一端固定在铁架台上,然后将最小刻度是毫
米的刻度尺竖直放在弹簧一侧,并使弹簧另一端的
指针恰好落在刻度尺上。当弹簧自然下垂时,指针
指示的刻度值记作L0;弹簧下端挂一个50 g的砝码时,
指针指示的刻度数值记作L1;弹簧下端挂两个50 g的
砝码时,指针指示的刻度数值记作L2;……挂七个50 g的砝码时,指针指示
的刻度数值记作L7。
(1)下表记录的是该同学已测出的6个值,其中有两个数值在记录时有误,它
们的代表符号分别是_____和______。
(2)测量记录表:
图2-4-8
代表符号 L0 L1 L2 L3 L4 L5 L6 L7
刻度数值/ cm 1.70 3.40 5.10 8.60 10.3 12.1
实验中,L3和L7两个值还没有测定,请你根据上图将这两个测量值填入记录表中。
(3)为充分利用测量数据,该同学将所测得的数值按如下方
法逐一求差,分别计算出了三个差值:d1=L4-L0=6.90 cm,
d2=L5-L1=6.90 cm,d3=L6-L2=7.00 cm。
请你给出第四个差值:d4=______=______ cm。
(4)根据以上差值,可以求出每增加50 g砝码的弹簧平均伸长
量 L。 L用d1、d2、d3、d4表示的式子为: L=________。
代入数据解得 L=_____ cm。
(5)计算弹簧的劲度系数k=______ N/m。(取g=9.8 m/s2)
(1)L5 L6
(2)6.85(6.84~6.86) 14.05(14.04~14.06)
(3)L7-L3 7.20(7.18~7.22)
(4)(d1+d2+d3+d4)/(4×4) 1.75
(5)28
同课章节目录
- 第一章 运动的描述
- 绪论
- 1 质点 参考系和坐标系
- 2 时间和位移
- 3 运动快慢的描述──速度
- 4 实验:用打点计时器测速度
- 5 速度变化快慢的描述──加速度
- 第二章 匀变速直线运动的研究
- 1 实验:探究小车速度随时间变化的规律
- 2 匀变速直线运动的速度与时间的关系
- 3 匀变速直线运动的位移与时间的关系
- 4 匀变速直线运动的位移与速度的关系
- 5 自由落体运动
- 6 伽利略对自由落体运动的研究
- 第三章 相互作用
- 1 重力 基本相互作用
- 2 弹力
- 3 摩擦力
- 4 力的合成
- 5 力的分解
- 第四章 牛顿运动定律
- 1 牛顿第一定律
- 2 实验:探究加速度与力、质量的关系
- 3 牛顿第二定律
- 4 力学单位制
- 5 牛顿第三定律
- 6 用牛顿定律解决问题(一)
- 7 用牛顿定律解决问题(二)
