高中物理 人教版(2019)必修第二册6.3 向心加速度课件(共35张PPT)
文档属性
| 名称 | 高中物理 人教版(2019)必修第二册6.3 向心加速度课件(共35张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.4MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(2019) | ||
| 科目 | 物理 | ||
| 更新时间 | 2021-11-16 16:08:11 | ||
图片预览










文档简介
(共35张PPT)
3.向心加速度
必备知识·自主学习
关键能力·合作探究
随堂演练·达标自测
学习目标
(1)知道向心加速度的概念.
(2)会用矢量图表示速度变化量与速度间的关系.
(3)能运用数学方法,结合加速度定义式推导向心加速度的公式.
必备知识·自主学习
一、匀速圆周运动的加速度方向
1.定义:物体做匀速圆周运动时的加速度总指向圆心,把它叫作向心加速度(centripetal acceleration).
2.方向:向心加速度的方向沿半径指向圆心,即向心加速度的方向与速度方向垂直.
导学:向心加速度与周期、转速、线速度、角速度关系的推导
由线速度与周期的关系v=代入a=得a=r.
由T=(n取r/s)代入a=
得a=4π2n2r.
由v=ωr代入a=得a==v·=ωv.
二、匀速圆周运动的加速度大小
1.推导:向心加速度与向心力的关系符合牛顿第二定律,则有:Fn=man=m=mω2r.
2.向心加速度公式:an=________=________.
3.作用效果:只改变线速度的方向,不改变线速度的大小.
w2r
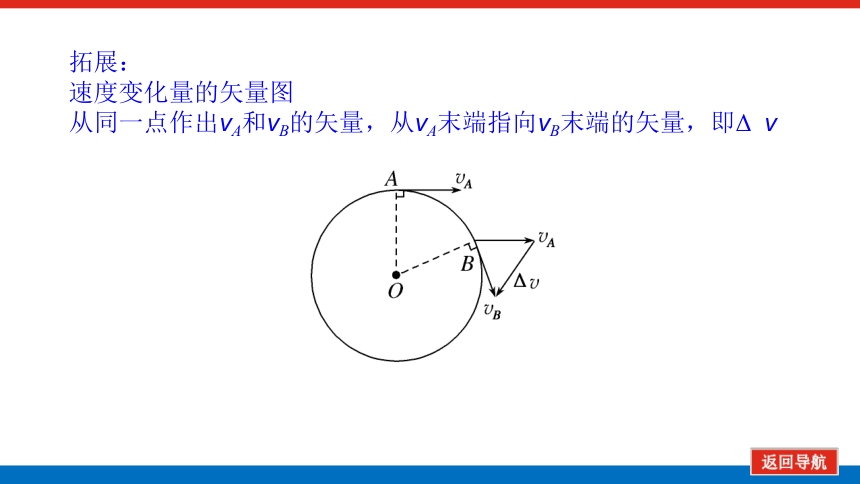
拓展:
速度变化量的矢量图
从同一点作出vA和vB的矢量,从vA末端指向vB末端的矢量,即Δ v
【思考辨析】 判断正误,正确的画“√”,错误的画“×”.
(1)匀速圆周运动是匀变速曲线运动.( )
(2)做匀速圆周运动的物体,其向心加速度恒定.( )
(3)物体做匀速圆周运动时,其相等时间内的位移相等.( )
(4)物体做匀速圆周运动时,相等时间内的速度变化量不同.( )
(5)根据an=可知加速度与半径成反比.( )
(6)根据an=ω2r可知当角速度一定时,加速度与半径成正比.( )
×
×
×
√
×
√
关键能力·合作探究
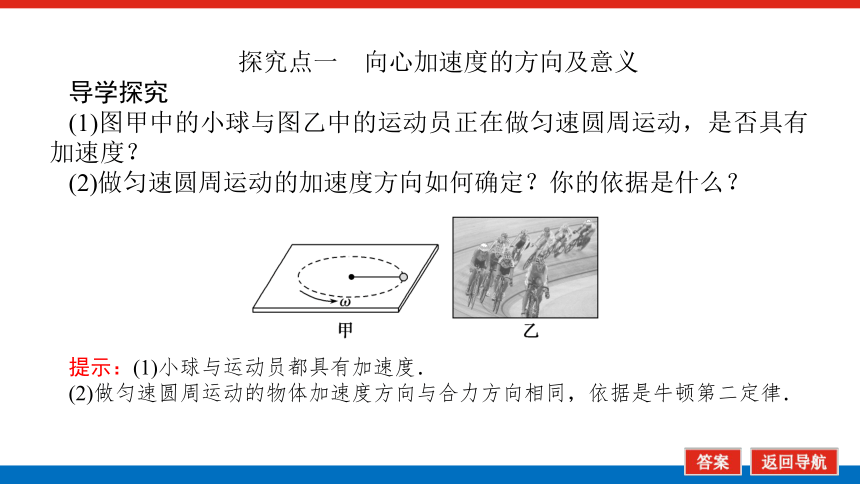
探究点一 向心加速度的方向及意义
导学探究
(1)图甲中的小球与图乙中的运动员正在做匀速圆周运动,是否具有加速度?
(2)做匀速圆周运动的加速度方向如何确定?你的依据是什么?
提示:(1)小球与运动员都具有加速度.
(2)做匀速圆周运动的物体加速度方向与合力方向相同,依据是牛顿第二定律.
探究总结
1.向心加速度的方向特点:
(1)指向圆心:无论匀速圆周运动,还是变速圆周运动,向心加速度的方向都指向圆心,或者说与线速度的方向垂直.
(2)时刻改变:无论向心加速度的大小是否变化,向心加速度的方向随线速度方向的改变而改变.所以一切圆周运动都是变加速曲线运动.
2.匀速圆周运动中的“变”与“不变”:
(1)“不变”量:匀速圆周运动的角速度、周期、转速不变;线速度、加速度这两个矢量的大小不变.
(2)“变化”量:匀速圆周运动的线速度、加速度这两个矢量的方向时刻改变.
3.物理意义:向心加速度描述圆周运动中线速度改变的快慢.
典例示范
【例1】 下列关于向心加速度的说法中正确的是( )
A.向心加速度表示做圆周运动的物体速率改变的快慢
B.匀速圆周运动的向心加速度是不变的
C.匀速圆周运动的向心加速度大小不变
D.只要是圆周运动,其加速度都是不变的
【解析】 圆周运动有两种情形:一是匀速圆周运动,二是非匀速圆周运动.在匀速圆周运动中,加速度的方向指向圆心,叫向心加速度,其大小不变,方向时刻改变;非匀速圆周运动中加速度可以分解为向心加速度和切向加速度,向心加速度改变线速度的方向,切向加速度改变线速度的大小.故选项C正确.
【答案】 C
练1 荡秋千是儿童喜爱的一项体育运动,如图所示,当秋千荡到最高点时,小孩的加速度方向是图中的( )
A.a方向 B.b方向
C.c方向 D.d方向
解析:当秋千荡到最高点时,小孩的速度为零,沿半径方向的向心加速度为零,加速度方向沿圆弧的切线方向,即图中的b方向,B正确.
答案:B
练2 (多选)关于匀速圆周运动和向心加速度,下列说法正确的是 ( )
A.匀速圆周运动的速度大小保持不变,所以做匀速圆周运动的物体没有加速度
B.做匀速圆周运动的物体,虽然速度大小不变,但方向时刻在变,所以必有加速度
C.做匀速圆周运动的物体,向心加速度的大小保持不变,所以是匀变速曲线运动
D.匀速圆周运动的向心加速度大小虽然不变,但方向始终指向圆心,时刻发生变化,所以匀速圆周运动不是匀变速运动
答案:BD
解析:做匀速圆周运动的物体,速度的大小不变,但方向时刻在变,所以必有加速度,且向心加速度大小不变,方向时刻指向圆心,向心加速度不恒定,因此匀速圆周运动不是匀变速运动,故A、C错误,B、D正确.
探究点二 向心加速度公式的理解与应用
探究总结
1.向心加速度公式
(1)基本公式:①an=,②an=ω2r.
(2)拓展公式:①an=r,②an=4π2n2r.
2.对向心加速度大小与半径关系的理解
(1)当r一定时,an∝v2,an∝ω2.
(2)当v一定时,an∝.
(3)当ω一定时,an∝r.
3.向心加速度与半径的关系:
典例示范
题型一 对向心加速度公式的理解
【例2】 (多选)如图所示为甲、乙两球在不同轨道上做匀速圆周运动的向心加速度随半径变化的图像,由图像可知( )
A.甲球运动时,线速度大小保持不变
B.甲球运动时,角速度大小保持不变
C.乙球运动时,线速度大小保持不变
D.乙球运动时,角速度大小保持不变
【解析】 A对,B错:由a=知,v不变时,a与R成反比,图像为双曲线的一支.C错,D对:由a=ω2R知,ω不变时,a与R成正比,图像为过原点的倾斜直线.
【答案】 AD
题型二 向心加速度公式的应用
【例3】飞机在做俯冲拉起运动时,可以看成是做圆周运动,如图所示,若在最低点附近做半径为R=240 m的圆周运动,飞行员的质量m=60 kg,飞机经过最低点P时的速度为v=360 km/h,试计算:
(1)此时飞机的向心加速度a的大小;
(2)此时飞行员对座椅的压力FN是多大.(g取10 m/s2)
解析】 (1)v=360 km/h=100 m/s
则a== m/s2= m/s2.
(2)对飞行员进行受力分析,则飞行员在最低点受重力和座椅的支持力,向心力由二力的合力提供.
所以FN-mg=ma
得FN=mg+ma
代入数据得FN=3 100 N
根据牛顿第三定律可知,飞行员对座椅的压力大小也为3 100 N.
题型三 传动装置中向心加速度的分析
【例4】如图所示,两轮用皮带传动,皮带不打滑.图中有A、B、C三点,这三点所在处半径关系为rA>rB=rC,则这三点的向心加速度aA、aB、aC之间的关系是( )
A.aA=aB=aC B.aC>aA>aB
C.aCaA
【解析】 A、B两点通过同一条皮带传动,线速度大小相等,即vA=vB,由于rA>rB,根据a=可知aArC,根据a=ω2r可知aC【答案】 C
思维方法
分析此类问题要“看”“找”“选”
练3 如图所示为两级皮带传动装置,转动时皮带均不打滑,中间两个轮子是固定在一起的,轮1的半径和轮2的半径相同,轮3的半径和轮4的半径相同,且为轮1和轮2半径的一半,则轮1边缘的a点和轮4边缘的c点相比 ( )
A.线速度之比为1∶4
B.角速度之比为4∶1
C.向心加速度之比为8∶1
D.向心加速度之比为1∶8
解析:A错:由题意知va=v3,v2=vc,又轮2与轮3同轴传动,角速度相同,v2=2v3,所以va∶vc=1∶2.B错:角速度之比为=∶=.C错,D对:设轮4的半径为r,则aa====ac,即aa∶ac=1∶8.
答案:D
练4 A、B两艘快艇在湖面上做匀速圆周运动(如图),在相同时间内,它们通过的路程之比是4∶3,运动方向改变的角度之比是3∶2,则它们( )
A.线速度大小之比为4∶3
B.角速度大小之比为3∶4
C.圆周运动的半径之比为2∶1
D.向心加速度大小之比为1∶2
解析:由圆周运动公式有,通过的路程s=Rθ=vt,转过的角度θ=ωt,已知在相同的时间内,通过的路程之比是4∶3,转过的角度之比是3∶2,则A、B的线速度大小之比是4∶3,角速度大小之比是3∶2,则选项A正确,B错误;由R=,得半径之比为=·==8∶9,由向心加速度a=ω2R,得向心加速度大小之比为=·==2∶1,选项C、D错误.
答案:A
随堂演练·达标自测
随堂演练·达标自测——突出创新性 素养达标
1.下列关于向心加速度的说法中正确的是( )
A.向心加速度越大,物体速率变化越快
B.向心加速度的大小与轨道半径成反比
C.向心加速度的方向始终与线速度的方向垂直
D.在匀速圆周运动中向心加速度是恒量
解析:A错:在匀速圆周运动中,速率不变.B错:向心加速度的大小可用an=或an=ω2r表示,当v一定时,an与r成反比;当ω一定时,an与r成正比.可见an与r的比例关系是有条件的.C对:向心加速度的方向始终与线速度的方向垂直.D错:在匀速圆周运动中,向心加速度的大小恒定,但方向始终指向圆心,即其方向时刻变化,所以向心加速度不是恒量.
答案:C
2. 转篮球是一项需要技巧的活动,如图所示,让篮球在指尖上匀速转动,指尖刚好静止在篮球球心的正下方.下列判断正确的是 ( )
A.篮球上的各点做圆周运动的圆心均在
指尖与篮球的接触处
B.篮球上各点的向心力是由手指提供的
C.篮球上各点做圆周运动的角速度相等
D.篮球上各点离转轴越近,做圆周运动
的向心加速度越大
答案:C
解析:A错:篮球上的各点做圆周运动的圆心在篮球的轴线上,类似于地球的自转轴.B错:手指并没有与篮球上别的点接触,不可能提供所有点的向心力.C对:篮球上各点做圆周运动的周期相等,角速度相等.D错:篮球上各点离转轴越近,由a=rω2可知,做圆周运动的向心加速度越小.
3.如图所示,一个凹形桥模拟器固定在水平地面上,其凹形轨道是半径为0.4 m的半圆,且在半圆最低点装有一个压力传感器(图中未画出).一质量为0.4 kg的玩具小车经过凹形轨道最低点时,传感器的示数为 8 N,则此时小车的(g取10 m/s2)( )
A.速度大小为1 m/s
B.速度大小为4 m/s
C.向心加速度大小为10 m/s2
D.向心加速度大小为20 m/s2
解析:当小车经过最低点时,受到的支持力与重力的合力提供向心力,则FN-mg=m,代入数据得v=2 m/s,向心加速度an==10 m/s2.
答案:C
4.如图所示,甲、乙、丙、丁四个可视为质点的小物体放置在匀速转动的水平转盘上,与转轴的距离分别为4r、2r、2r、r,甲、丙位于转盘的边缘处,两转盘边缘接触,靠摩擦传递动力,转盘与转盘之间、物体与盘面之间均未发生相对滑动,则向心加速度最大的是( )
A.甲 B.乙 C.丙 D.丁
解析:先根据an=ω2r分析同一转盘上两物体的向心加速度关系,再根据an=分析不同转盘上两物体的向心加速度关系.所以选项C正确.
答案:C
5.如图所示,自行车的小齿轮A、大齿轮B、后轮C是相互关联的三个转动部分,且半径RB=4RA、RC=8RA.当自行车正常骑行时,A、B、C三轮边缘的向心加速度的大小之比aA∶aB∶aC等于( )
A.1∶1∶8 B.4∶1∶4
C.4∶1∶32 D.1∶2∶4
解析:A、B的线速度大小相等,RA∶RB=1∶4,根据a=知,aA∶aB=4∶1.A、C的角速度大小相等,RA∶RC=1∶8,根据a=ω2r知,aA∶aC=1∶8,所以aA∶aB∶aC=4∶1∶32.
答案:C
3.向心加速度
必备知识·自主学习
关键能力·合作探究
随堂演练·达标自测
学习目标
(1)知道向心加速度的概念.
(2)会用矢量图表示速度变化量与速度间的关系.
(3)能运用数学方法,结合加速度定义式推导向心加速度的公式.
必备知识·自主学习
一、匀速圆周运动的加速度方向
1.定义:物体做匀速圆周运动时的加速度总指向圆心,把它叫作向心加速度(centripetal acceleration).
2.方向:向心加速度的方向沿半径指向圆心,即向心加速度的方向与速度方向垂直.
导学:向心加速度与周期、转速、线速度、角速度关系的推导
由线速度与周期的关系v=代入a=得a=r.
由T=(n取r/s)代入a=
得a=4π2n2r.
由v=ωr代入a=得a==v·=ωv.
二、匀速圆周运动的加速度大小
1.推导:向心加速度与向心力的关系符合牛顿第二定律,则有:Fn=man=m=mω2r.
2.向心加速度公式:an=________=________.
3.作用效果:只改变线速度的方向,不改变线速度的大小.
w2r
拓展:
速度变化量的矢量图
从同一点作出vA和vB的矢量,从vA末端指向vB末端的矢量,即Δ v
【思考辨析】 判断正误,正确的画“√”,错误的画“×”.
(1)匀速圆周运动是匀变速曲线运动.( )
(2)做匀速圆周运动的物体,其向心加速度恒定.( )
(3)物体做匀速圆周运动时,其相等时间内的位移相等.( )
(4)物体做匀速圆周运动时,相等时间内的速度变化量不同.( )
(5)根据an=可知加速度与半径成反比.( )
(6)根据an=ω2r可知当角速度一定时,加速度与半径成正比.( )
×
×
×
√
×
√
关键能力·合作探究
探究点一 向心加速度的方向及意义
导学探究
(1)图甲中的小球与图乙中的运动员正在做匀速圆周运动,是否具有加速度?
(2)做匀速圆周运动的加速度方向如何确定?你的依据是什么?
提示:(1)小球与运动员都具有加速度.
(2)做匀速圆周运动的物体加速度方向与合力方向相同,依据是牛顿第二定律.
探究总结
1.向心加速度的方向特点:
(1)指向圆心:无论匀速圆周运动,还是变速圆周运动,向心加速度的方向都指向圆心,或者说与线速度的方向垂直.
(2)时刻改变:无论向心加速度的大小是否变化,向心加速度的方向随线速度方向的改变而改变.所以一切圆周运动都是变加速曲线运动.
2.匀速圆周运动中的“变”与“不变”:
(1)“不变”量:匀速圆周运动的角速度、周期、转速不变;线速度、加速度这两个矢量的大小不变.
(2)“变化”量:匀速圆周运动的线速度、加速度这两个矢量的方向时刻改变.
3.物理意义:向心加速度描述圆周运动中线速度改变的快慢.
典例示范
【例1】 下列关于向心加速度的说法中正确的是( )
A.向心加速度表示做圆周运动的物体速率改变的快慢
B.匀速圆周运动的向心加速度是不变的
C.匀速圆周运动的向心加速度大小不变
D.只要是圆周运动,其加速度都是不变的
【解析】 圆周运动有两种情形:一是匀速圆周运动,二是非匀速圆周运动.在匀速圆周运动中,加速度的方向指向圆心,叫向心加速度,其大小不变,方向时刻改变;非匀速圆周运动中加速度可以分解为向心加速度和切向加速度,向心加速度改变线速度的方向,切向加速度改变线速度的大小.故选项C正确.
【答案】 C
练1 荡秋千是儿童喜爱的一项体育运动,如图所示,当秋千荡到最高点时,小孩的加速度方向是图中的( )
A.a方向 B.b方向
C.c方向 D.d方向
解析:当秋千荡到最高点时,小孩的速度为零,沿半径方向的向心加速度为零,加速度方向沿圆弧的切线方向,即图中的b方向,B正确.
答案:B
练2 (多选)关于匀速圆周运动和向心加速度,下列说法正确的是 ( )
A.匀速圆周运动的速度大小保持不变,所以做匀速圆周运动的物体没有加速度
B.做匀速圆周运动的物体,虽然速度大小不变,但方向时刻在变,所以必有加速度
C.做匀速圆周运动的物体,向心加速度的大小保持不变,所以是匀变速曲线运动
D.匀速圆周运动的向心加速度大小虽然不变,但方向始终指向圆心,时刻发生变化,所以匀速圆周运动不是匀变速运动
答案:BD
解析:做匀速圆周运动的物体,速度的大小不变,但方向时刻在变,所以必有加速度,且向心加速度大小不变,方向时刻指向圆心,向心加速度不恒定,因此匀速圆周运动不是匀变速运动,故A、C错误,B、D正确.
探究点二 向心加速度公式的理解与应用
探究总结
1.向心加速度公式
(1)基本公式:①an=,②an=ω2r.
(2)拓展公式:①an=r,②an=4π2n2r.
2.对向心加速度大小与半径关系的理解
(1)当r一定时,an∝v2,an∝ω2.
(2)当v一定时,an∝.
(3)当ω一定时,an∝r.
3.向心加速度与半径的关系:
典例示范
题型一 对向心加速度公式的理解
【例2】 (多选)如图所示为甲、乙两球在不同轨道上做匀速圆周运动的向心加速度随半径变化的图像,由图像可知( )
A.甲球运动时,线速度大小保持不变
B.甲球运动时,角速度大小保持不变
C.乙球运动时,线速度大小保持不变
D.乙球运动时,角速度大小保持不变
【解析】 A对,B错:由a=知,v不变时,a与R成反比,图像为双曲线的一支.C错,D对:由a=ω2R知,ω不变时,a与R成正比,图像为过原点的倾斜直线.
【答案】 AD
题型二 向心加速度公式的应用
【例3】飞机在做俯冲拉起运动时,可以看成是做圆周运动,如图所示,若在最低点附近做半径为R=240 m的圆周运动,飞行员的质量m=60 kg,飞机经过最低点P时的速度为v=360 km/h,试计算:
(1)此时飞机的向心加速度a的大小;
(2)此时飞行员对座椅的压力FN是多大.(g取10 m/s2)
解析】 (1)v=360 km/h=100 m/s
则a== m/s2= m/s2.
(2)对飞行员进行受力分析,则飞行员在最低点受重力和座椅的支持力,向心力由二力的合力提供.
所以FN-mg=ma
得FN=mg+ma
代入数据得FN=3 100 N
根据牛顿第三定律可知,飞行员对座椅的压力大小也为3 100 N.
题型三 传动装置中向心加速度的分析
【例4】如图所示,两轮用皮带传动,皮带不打滑.图中有A、B、C三点,这三点所在处半径关系为rA>rB=rC,则这三点的向心加速度aA、aB、aC之间的关系是( )
A.aA=aB=aC B.aC>aA>aB
C.aC
【解析】 A、B两点通过同一条皮带传动,线速度大小相等,即vA=vB,由于rA>rB,根据a=可知aA
思维方法
分析此类问题要“看”“找”“选”
练3 如图所示为两级皮带传动装置,转动时皮带均不打滑,中间两个轮子是固定在一起的,轮1的半径和轮2的半径相同,轮3的半径和轮4的半径相同,且为轮1和轮2半径的一半,则轮1边缘的a点和轮4边缘的c点相比 ( )
A.线速度之比为1∶4
B.角速度之比为4∶1
C.向心加速度之比为8∶1
D.向心加速度之比为1∶8
解析:A错:由题意知va=v3,v2=vc,又轮2与轮3同轴传动,角速度相同,v2=2v3,所以va∶vc=1∶2.B错:角速度之比为=∶=.C错,D对:设轮4的半径为r,则aa====ac,即aa∶ac=1∶8.
答案:D
练4 A、B两艘快艇在湖面上做匀速圆周运动(如图),在相同时间内,它们通过的路程之比是4∶3,运动方向改变的角度之比是3∶2,则它们( )
A.线速度大小之比为4∶3
B.角速度大小之比为3∶4
C.圆周运动的半径之比为2∶1
D.向心加速度大小之比为1∶2
解析:由圆周运动公式有,通过的路程s=Rθ=vt,转过的角度θ=ωt,已知在相同的时间内,通过的路程之比是4∶3,转过的角度之比是3∶2,则A、B的线速度大小之比是4∶3,角速度大小之比是3∶2,则选项A正确,B错误;由R=,得半径之比为=·==8∶9,由向心加速度a=ω2R,得向心加速度大小之比为=·==2∶1,选项C、D错误.
答案:A
随堂演练·达标自测
随堂演练·达标自测——突出创新性 素养达标
1.下列关于向心加速度的说法中正确的是( )
A.向心加速度越大,物体速率变化越快
B.向心加速度的大小与轨道半径成反比
C.向心加速度的方向始终与线速度的方向垂直
D.在匀速圆周运动中向心加速度是恒量
解析:A错:在匀速圆周运动中,速率不变.B错:向心加速度的大小可用an=或an=ω2r表示,当v一定时,an与r成反比;当ω一定时,an与r成正比.可见an与r的比例关系是有条件的.C对:向心加速度的方向始终与线速度的方向垂直.D错:在匀速圆周运动中,向心加速度的大小恒定,但方向始终指向圆心,即其方向时刻变化,所以向心加速度不是恒量.
答案:C
2. 转篮球是一项需要技巧的活动,如图所示,让篮球在指尖上匀速转动,指尖刚好静止在篮球球心的正下方.下列判断正确的是 ( )
A.篮球上的各点做圆周运动的圆心均在
指尖与篮球的接触处
B.篮球上各点的向心力是由手指提供的
C.篮球上各点做圆周运动的角速度相等
D.篮球上各点离转轴越近,做圆周运动
的向心加速度越大
答案:C
解析:A错:篮球上的各点做圆周运动的圆心在篮球的轴线上,类似于地球的自转轴.B错:手指并没有与篮球上别的点接触,不可能提供所有点的向心力.C对:篮球上各点做圆周运动的周期相等,角速度相等.D错:篮球上各点离转轴越近,由a=rω2可知,做圆周运动的向心加速度越小.
3.如图所示,一个凹形桥模拟器固定在水平地面上,其凹形轨道是半径为0.4 m的半圆,且在半圆最低点装有一个压力传感器(图中未画出).一质量为0.4 kg的玩具小车经过凹形轨道最低点时,传感器的示数为 8 N,则此时小车的(g取10 m/s2)( )
A.速度大小为1 m/s
B.速度大小为4 m/s
C.向心加速度大小为10 m/s2
D.向心加速度大小为20 m/s2
解析:当小车经过最低点时,受到的支持力与重力的合力提供向心力,则FN-mg=m,代入数据得v=2 m/s,向心加速度an==10 m/s2.
答案:C
4.如图所示,甲、乙、丙、丁四个可视为质点的小物体放置在匀速转动的水平转盘上,与转轴的距离分别为4r、2r、2r、r,甲、丙位于转盘的边缘处,两转盘边缘接触,靠摩擦传递动力,转盘与转盘之间、物体与盘面之间均未发生相对滑动,则向心加速度最大的是( )
A.甲 B.乙 C.丙 D.丁
解析:先根据an=ω2r分析同一转盘上两物体的向心加速度关系,再根据an=分析不同转盘上两物体的向心加速度关系.所以选项C正确.
答案:C
5.如图所示,自行车的小齿轮A、大齿轮B、后轮C是相互关联的三个转动部分,且半径RB=4RA、RC=8RA.当自行车正常骑行时,A、B、C三轮边缘的向心加速度的大小之比aA∶aB∶aC等于( )
A.1∶1∶8 B.4∶1∶4
C.4∶1∶32 D.1∶2∶4
解析:A、B的线速度大小相等,RA∶RB=1∶4,根据a=知,aA∶aB=4∶1.A、C的角速度大小相等,RA∶RC=1∶8,根据a=ω2r知,aA∶aC=1∶8,所以aA∶aB∶aC=4∶1∶32.
答案:C
