人教版数学九年级下册第二十七章 相似27.2.2相似三角形的性质 课件(共23张PPT)
文档属性
| 名称 | 人教版数学九年级下册第二十七章 相似27.2.2相似三角形的性质 课件(共23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 00:00:00 | ||
图片预览






文档简介
(共23张PPT)
27.2.2相似三角形
的性质
Part 1
新知 导入
新知导入
1.三角形相似的判定方法有那些?
两个角对应相等的两个三角形相似。
两边对应成比例且夹角相等的两个三角形相似 。
三边对应成比例的两个三角形相似。
2.相似三角形的有哪些性质
相似三角形的_________________, 各对应边——————。
对应角相等
成比例
思考?
相似三角形还有哪些性质
Part2
探索 新知
新知讲解
如图,已知△ABC∽△ A′B′C′,相似比是k,其中AD 、 A′D′分别是BC 、 B′C′边 上的高。
1)△ABD 与△ A′B′D′相似吗?
∵△ABC∽△ A′B′C′
∴∠B=∠B′(相似三角形对应角相等)
又∠ADB=∠A ′ D ′ B′ = 90°
∴△ABD ∽△ A′B′D′(两个角对应相等的两个三角形相似)
2) AD 、 A′D′有什么关系呢?
∵ △ABD ∽△ A′B′D′
=
B′
A′
k
=
AB
A′D′
AD
∴
结论:相似三角形对应高的比等于相似比
新知讲解
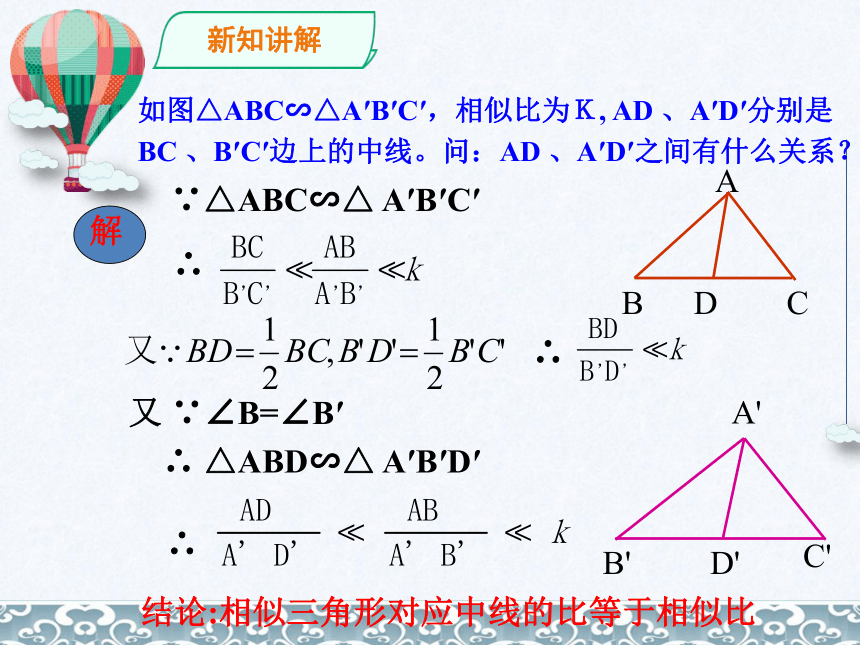
如图△ABC∽△A′B′C′,相似比为K, AD 、A′D′分别是
BC 、B′C′边上的中线。问:AD 、A′D′之间有什么关系?
解
∵△ABC∽△ A′B′C′
∴
∴
又 ∵∠B=∠B′
∴ △ABD∽△ A′B′D′
∴
结论:相似三角形对应中线的比等于相似比
D
C
B
A
D'
C'
B'
A'
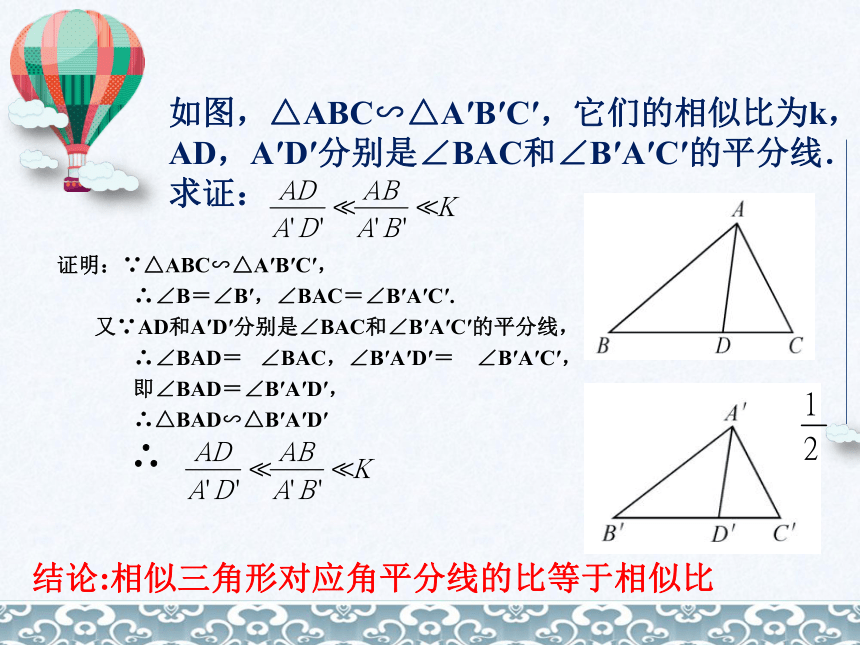
如图,△ABC∽△A′B′C′,它们的相似比为k,
AD,A′D′分别是∠BAC和∠B′A′C′的平分线.
求证:
证明:∵△ABC∽△A′B′C′,
∴∠B=∠B′,∠BAC=∠B′A′C′.
又∵AD和A′D′分别是∠BAC和∠B′A′C′的平分线,
∴∠BAD= ∠BAC,∠B′A′D′= ∠B′A′C′,
即∠BAD=∠B′A′D′,
∴△BAD∽△B′A′D′
∴
结论:相似三角形对应角平分线的比等于相似比
新知讲解
角平分线
角平分线
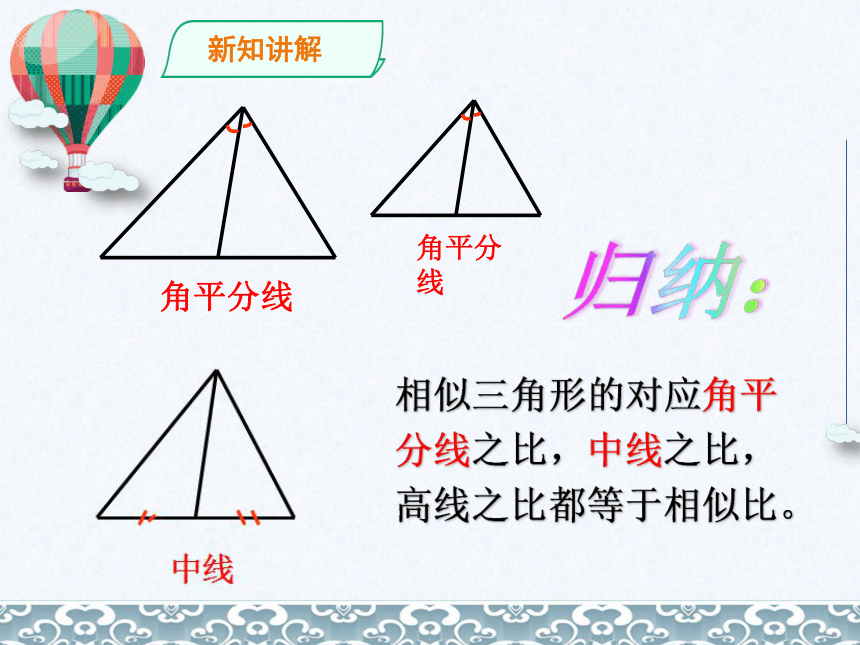
归纳:
相似三角形的对应角平分线之比,中线之比,高线之比都等于相似比。
巩固练习
1、已知△ABC∽△A B C ,AD、A D 分别是对应
边BC、B C 上的高,若BC=8cm,B C =6cm,
AD=4cm,则A D 等于( )
A 16cm B 12 cm C 3 cm D 6 cm
C
2、两个相似三角形对应高的比为3∶7,它们的
对应角平分线的比为( )
A 7∶3 B 49∶9 C 9∶49 D 3∶7
D
思考
如果两个三角形相似,它们的周长之间有什么
关系?两个相似多边形呢?
相似三角形周长的比等于相似比。
相似多边形周长的比等于相似比。
A
B
C
A/
B/
C/
思考?
(1)如图ΔABC∽ΔA/B/C/ ,相似比为k,
它们的面积比是多少?
A
B
C
D
A /
B /
C /
D /
①相似三角形面积的比等于相似比的平方.
思考?
(2)如图,四边ABCD相似于四边形A'B'C'D'
,相似比为k,它们的面积比是多少?
A
B
C
D
A /
B /
C /
D /
②相似多边形面积的比等于相似比的平方.
相似三角形(多边形)的性质:
(1)相似三角形对应的 比等于相似比.
中线
高线
角平分线
(2)相似 周长的比等于相似比.
三角形
多边形
(3)相似 面积的比等于相似比的平方.
三角形
多边形
Part 3
巩固 练习
(三)知识应用,拓展思维
填空:
(1)如果两个相似三角形对应边的比为3∶5 ,那么它们的相似比为________,周长的比为______,面积的比为________.
(2)如果两个相似三角形面积的比为3∶5 ,那么它们的相似比为________,周长的比为______.
(3)连结三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于______.
(4)两个相似三角形对应的中线长分别是6 cm
和18 cm,若较大三角形的周长是42 cm ,面积
是12 cm 2,则较小三角形的周长为________cm
,面积为_____cm 2.
判断题:
(1)如果把一个三角形各边同时扩大为原来的5倍,那么它的周长也扩大为原来的5倍。
(2)如果把一个三角形的面积扩大为原来的9倍,那么它的三边也扩大为原来的9倍。
拓展提高
如图,在△ABC中,D是AB的中点,
DE∥ BC,则:
(1)S △ADE : S △ABC =
(2)S △ADE: S 梯形DBCE =
拓展提高
如图,△ABC,DE// FG// BC ,且△ADE的面积,梯形FBCG的面积,梯形DFGE的面积均相等,则△ADE与△ABC的
相似比是_____________;
△AFG与△ABC的
相似比是_____________.
B
A
D
E
C
F
G
拓展提高
Part 4
总结 归纳
课堂总结
结论:相似三角形对应高的比等于相似比.
结论:相似三角形对应中线的比等于相似比.
结论:相似三角形对应角平分线的比等于相似比.
结论:相似三角形面积的比等于相似比的平方.
结论:相似四边形面积的比等于相似比的平方.
结论:相似多边形面积的比等于相似比的平方.
Thanks
27.2.2相似三角形
的性质
Part 1
新知 导入
新知导入
1.三角形相似的判定方法有那些?
两个角对应相等的两个三角形相似。
两边对应成比例且夹角相等的两个三角形相似 。
三边对应成比例的两个三角形相似。
2.相似三角形的有哪些性质
相似三角形的_________________, 各对应边——————。
对应角相等
成比例
思考?
相似三角形还有哪些性质
Part2
探索 新知
新知讲解
如图,已知△ABC∽△ A′B′C′,相似比是k,其中AD 、 A′D′分别是BC 、 B′C′边 上的高。
1)△ABD 与△ A′B′D′相似吗?
∵△ABC∽△ A′B′C′
∴∠B=∠B′(相似三角形对应角相等)
又∠ADB=∠A ′ D ′ B′ = 90°
∴△ABD ∽△ A′B′D′(两个角对应相等的两个三角形相似)
2) AD 、 A′D′有什么关系呢?
∵ △ABD ∽△ A′B′D′
=
B′
A′
k
=
AB
A′D′
AD
∴
结论:相似三角形对应高的比等于相似比
新知讲解
如图△ABC∽△A′B′C′,相似比为K, AD 、A′D′分别是
BC 、B′C′边上的中线。问:AD 、A′D′之间有什么关系?
解
∵△ABC∽△ A′B′C′
∴
∴
又 ∵∠B=∠B′
∴ △ABD∽△ A′B′D′
∴
结论:相似三角形对应中线的比等于相似比
D
C
B
A
D'
C'
B'
A'
如图,△ABC∽△A′B′C′,它们的相似比为k,
AD,A′D′分别是∠BAC和∠B′A′C′的平分线.
求证:
证明:∵△ABC∽△A′B′C′,
∴∠B=∠B′,∠BAC=∠B′A′C′.
又∵AD和A′D′分别是∠BAC和∠B′A′C′的平分线,
∴∠BAD= ∠BAC,∠B′A′D′= ∠B′A′C′,
即∠BAD=∠B′A′D′,
∴△BAD∽△B′A′D′
∴
结论:相似三角形对应角平分线的比等于相似比
新知讲解
角平分线
角平分线
归纳:
相似三角形的对应角平分线之比,中线之比,高线之比都等于相似比。
巩固练习
1、已知△ABC∽△A B C ,AD、A D 分别是对应
边BC、B C 上的高,若BC=8cm,B C =6cm,
AD=4cm,则A D 等于( )
A 16cm B 12 cm C 3 cm D 6 cm
C
2、两个相似三角形对应高的比为3∶7,它们的
对应角平分线的比为( )
A 7∶3 B 49∶9 C 9∶49 D 3∶7
D
思考
如果两个三角形相似,它们的周长之间有什么
关系?两个相似多边形呢?
相似三角形周长的比等于相似比。
相似多边形周长的比等于相似比。
A
B
C
A/
B/
C/
思考?
(1)如图ΔABC∽ΔA/B/C/ ,相似比为k,
它们的面积比是多少?
A
B
C
D
A /
B /
C /
D /
①相似三角形面积的比等于相似比的平方.
思考?
(2)如图,四边ABCD相似于四边形A'B'C'D'
,相似比为k,它们的面积比是多少?
A
B
C
D
A /
B /
C /
D /
②相似多边形面积的比等于相似比的平方.
相似三角形(多边形)的性质:
(1)相似三角形对应的 比等于相似比.
中线
高线
角平分线
(2)相似 周长的比等于相似比.
三角形
多边形
(3)相似 面积的比等于相似比的平方.
三角形
多边形
Part 3
巩固 练习
(三)知识应用,拓展思维
填空:
(1)如果两个相似三角形对应边的比为3∶5 ,那么它们的相似比为________,周长的比为______,面积的比为________.
(2)如果两个相似三角形面积的比为3∶5 ,那么它们的相似比为________,周长的比为______.
(3)连结三角形两边中点的线段把三角形截成的一个小三角形与原三角形的周长比等于______,面积比等于______.
(4)两个相似三角形对应的中线长分别是6 cm
和18 cm,若较大三角形的周长是42 cm ,面积
是12 cm 2,则较小三角形的周长为________cm
,面积为_____cm 2.
判断题:
(1)如果把一个三角形各边同时扩大为原来的5倍,那么它的周长也扩大为原来的5倍。
(2)如果把一个三角形的面积扩大为原来的9倍,那么它的三边也扩大为原来的9倍。
拓展提高
如图,在△ABC中,D是AB的中点,
DE∥ BC,则:
(1)S △ADE : S △ABC =
(2)S △ADE: S 梯形DBCE =
拓展提高
如图,△ABC,DE// FG// BC ,且△ADE的面积,梯形FBCG的面积,梯形DFGE的面积均相等,则△ADE与△ABC的
相似比是_____________;
△AFG与△ABC的
相似比是_____________.
B
A
D
E
C
F
G
拓展提高
Part 4
总结 归纳
课堂总结
结论:相似三角形对应高的比等于相似比.
结论:相似三角形对应中线的比等于相似比.
结论:相似三角形对应角平分线的比等于相似比.
结论:相似三角形面积的比等于相似比的平方.
结论:相似四边形面积的比等于相似比的平方.
结论:相似多边形面积的比等于相似比的平方.
Thanks
