2021-2022学年人教版数学九年级上册24.2.2 直线和圆的位置关系(2)课件(共19张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学九年级上册24.2.2 直线和圆的位置关系(2)课件(共19张PPT) |
|
|
| 格式 | zip | ||
| 文件大小 | 714.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 09:39:27 | ||
图片预览




文档简介
(共19张PPT)
复习检测
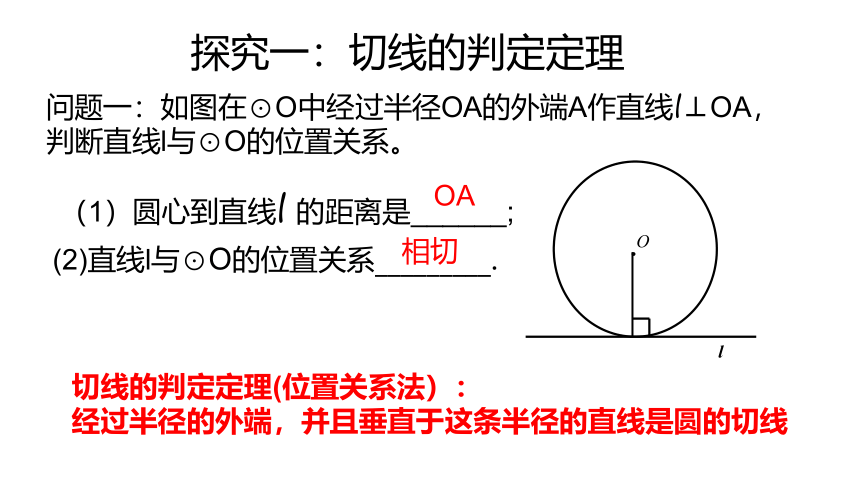
回顾直线与圆的位置关系
设⊙O的半径为r,圆心到直线l的距离为d,可以看出
若d若d=r,直线与⊙O____________
若d>r,直线与⊙O____________
相交
相切
相离
思考:你是怎样判定直线是圆的切线的呢?
1、定义法:与圆只有一个交点的直线是圆的切线;
2、数量关系法:圆心到直线的距离d与半径r 相等时,直线与圆相切。
3、能否从这条直线与某条特定半径的位置关系来判定呢?
24.2.2 直线和圆的位置关系
第2课时 切线的判定与性质
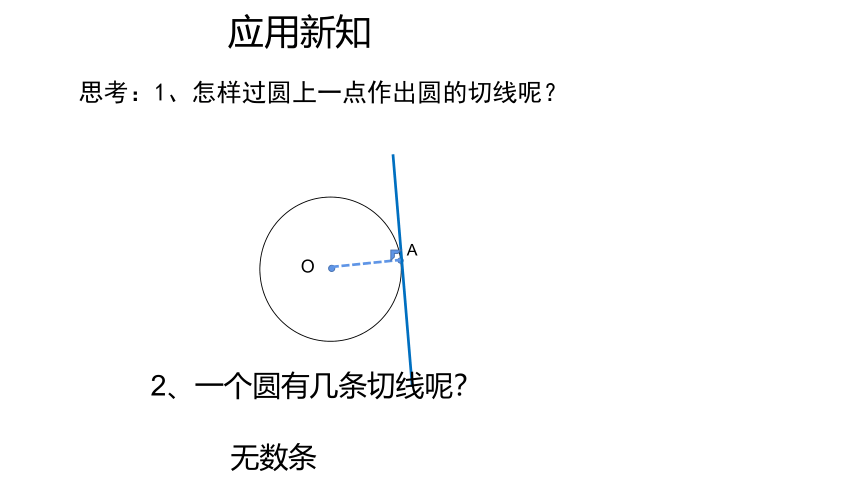
问题一:如图在⊙O中经过半径OA的外端A作直线l⊥OA,
判断直线l与⊙O的位置关系。
O
l
(1)圆心到直线l 的距离是______;
(2)直线l与⊙O的位置关系_________.
切线的判定定理(位置关系法):
经过半径的外端,并且垂直于这条半径的直线是圆的切线
探究一:切线的判定定理
OA
相切
A
O
思考:1、怎样过圆上一点作出圆的切线呢?
应用新知
2、一个圆有几条切线呢?
无数条
例1 如图, 直线AB经过⊙O上的点C,并且OA=OB, CA=CB. 求证:直线AB是⊙O的切线.
A
C
B
O
分析:由于AB过⊙O上的点C,所以连接OC,只要证明AB⊥OC即可.
证明:连接OC ,
∵ CA=CB
∴ C是AB 的中点
∵ OA=OB
∴ OA⊥OC
∴ 直线AB是⊙O的切线.
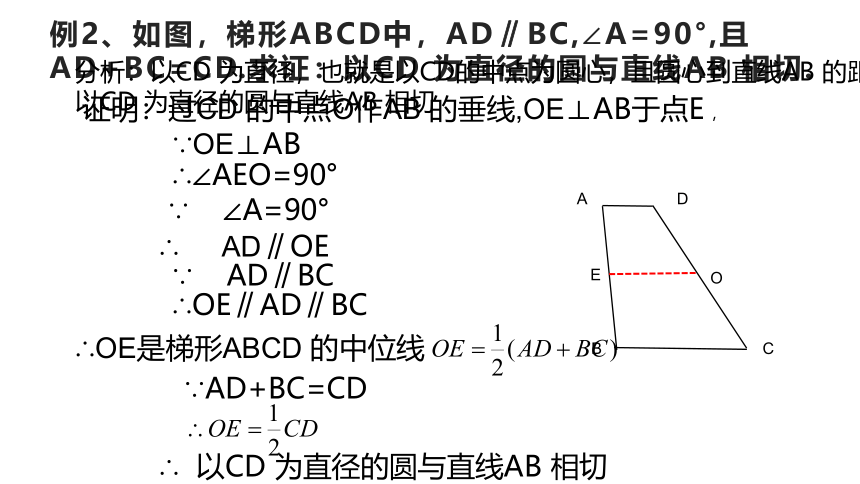
例2、如图,梯形ABCD中,AD∥BC,∠A=90°,且AD+BC=CD.求证:以CD 为直径的圆与直线AB 相切.
A
B
C
D
分析:以CD 为直径,也就是以CD的中点为圆心,且圆心到直线AB 的距离等于半径时,
以CD 为直径的圆与直线AB 相切
证明:过CD 的中点O作AB 的垂线,OE⊥AB于点E ,
O
E
∵OE⊥AB
∴∠AEO=90°
∵ ∠A=90°
∴ AD∥OE
∵ AD∥BC
∴OE∥AD∥BC
∴OE是梯形ABCD 的中位线
∵AD+BC=CD
∴ 以CD 为直径的圆与直线AB 相切
(1) 当证明某直线是圆的切线时,如果已知直线过圆上一点,则作出过这一点的半径,证明直线垂直于半径,简记为“连半径,证垂直” ;(例1)
(2) 如果直线和圆的公共点没有确定,则应过圆心作直线的垂线,证明圆心到直线的距离等于半径,简记为“作垂直,证距离等于半径”(例2)
证切线时辅助线的添加方法
要点归纳
实际生活中的切线
1.下雨天快速转动的雨伞,飞出的水珠所在直线与圆相切,
2.在砂轮上打磨工件时,飞出的火星所在的轨迹与砂轮相切
3.打陀螺时,绳子与陀螺是相切的关系
思考:如图,如果直线l是⊙O 的切线,点A为切点,那么OA与直线l垂直吗?
A
l
O
探究二:切线的性质定理
结论:半径OA与直线l垂直
如何证明你的结论呢?
分析:直线l与半径OA的位置关系只有两种位置关系:要么直线l垂直于OA,要么直线l不垂直于OA,否定一个位置关系,肯定另一个位置关系成立。
证明:假设直线l不垂直于OA
过点O作OM⊥l (作垂线段)
∴ OMOM(d)∴直线l与⊙O相交
这与条件直线l与⊙O相切相矛盾,顾假设不成立。
∴l⊥OA
切线的性质定理 :
圆的切线垂直于经过切点的半径.
∵直线l是⊙O 的切线,A是切点,
∴直线l ⊥OA.
A
l
O
几何语言:
例 已知:△ABC 为等腰三角形,O 是底边 BC 的中点,AB 与⊙O 相切于点 D.
求证: AC 是⊙O 的切线.
A
B
O
D
C
证明:如图,过点O作OE⊥AC,
垂足为E,连接OD,OA.
∵⊙O与AB相切于点D,
∴OD⊥AB.
又△ABC为等腰三角形,
O是底边BC的中点,
∴AO是∠BAC的平分线.
∴OE=OD,即OE是⊙O的半径.
∵AC经过⊙O的半径OE的外端E,并且垂直于半径OE
∴AC与⊙O相切.
A
B
O
D
C
E
证明:连接DO,
∵点D是BC的中点,
∴CD=BD.
∵AB是直径,
∴∠ADB=90°
∴AD⊥BC.
∴AC=AB
∴∠C=∠B.
随堂练习
1.如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于点E,连接AD,求证:DE是⊙O的切线.
∵OD=OB
∴∠B=∠ODB,
∴∠ODB=∠C
∴OD∥AC.
∵DE⊥AC,
∴∠ODE=∠CED=90°
∴DE⊥OD.
∴ED是⊙O的切线.
2.如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连接AC,将△ACE沿AC翻折得到△ACF,直线FC与直线AB相交于点G.
(1)直线FC与⊙O有何位置关系?并说明理由;
(2)若OB=BG=2,求CD的长.
解:(1)直线FC与⊙O相切.
理由如下:连接OC.
∵OA=OC,
∴∠1=∠2.
由翻折,得∠1=∠3,∠F=∠AEC=90°.
∴∠2=∠3.
∴OC∥AF.
∴∠OCG=∠F=90°.
∴OC⊥FG.
∴直线FC与⊙O相切.
(2)∵直线GF与⊙O相切,
∴OC⊥FG.
∵OC=OB=BG,∴∠G=30°.
∴∠COG=60°,∴∠OCE=30°.
∴OE=1.∴CE= .
∵直径AB垂直于弦CD,
∴
课堂小结
1、切线的判定方法
2、切线的性质
(1)定义法
(2)数量关系法
(3)切线的判定定理
(1)切线的性质定理
(2)直线与圆只有1个公共点
(3)d=r
3、证切线时常用辅助线添加方法:
①有公共点,连半径,证垂直;
②无公共点,作垂直,证半径
复习检测
回顾直线与圆的位置关系
设⊙O的半径为r,圆心到直线l的距离为d,可以看出
若d
若d>r,直线与⊙O____________
相交
相切
相离
思考:你是怎样判定直线是圆的切线的呢?
1、定义法:与圆只有一个交点的直线是圆的切线;
2、数量关系法:圆心到直线的距离d与半径r 相等时,直线与圆相切。
3、能否从这条直线与某条特定半径的位置关系来判定呢?
24.2.2 直线和圆的位置关系
第2课时 切线的判定与性质
问题一:如图在⊙O中经过半径OA的外端A作直线l⊥OA,
判断直线l与⊙O的位置关系。
O
l
(1)圆心到直线l 的距离是______;
(2)直线l与⊙O的位置关系_________.
切线的判定定理(位置关系法):
经过半径的外端,并且垂直于这条半径的直线是圆的切线
探究一:切线的判定定理
OA
相切
A
O
思考:1、怎样过圆上一点作出圆的切线呢?
应用新知
2、一个圆有几条切线呢?
无数条
例1 如图, 直线AB经过⊙O上的点C,并且OA=OB, CA=CB. 求证:直线AB是⊙O的切线.
A
C
B
O
分析:由于AB过⊙O上的点C,所以连接OC,只要证明AB⊥OC即可.
证明:连接OC ,
∵ CA=CB
∴ C是AB 的中点
∵ OA=OB
∴ OA⊥OC
∴ 直线AB是⊙O的切线.
例2、如图,梯形ABCD中,AD∥BC,∠A=90°,且AD+BC=CD.求证:以CD 为直径的圆与直线AB 相切.
A
B
C
D
分析:以CD 为直径,也就是以CD的中点为圆心,且圆心到直线AB 的距离等于半径时,
以CD 为直径的圆与直线AB 相切
证明:过CD 的中点O作AB 的垂线,OE⊥AB于点E ,
O
E
∵OE⊥AB
∴∠AEO=90°
∵ ∠A=90°
∴ AD∥OE
∵ AD∥BC
∴OE∥AD∥BC
∴OE是梯形ABCD 的中位线
∵AD+BC=CD
∴ 以CD 为直径的圆与直线AB 相切
(1) 当证明某直线是圆的切线时,如果已知直线过圆上一点,则作出过这一点的半径,证明直线垂直于半径,简记为“连半径,证垂直” ;(例1)
(2) 如果直线和圆的公共点没有确定,则应过圆心作直线的垂线,证明圆心到直线的距离等于半径,简记为“作垂直,证距离等于半径”(例2)
证切线时辅助线的添加方法
要点归纳
实际生活中的切线
1.下雨天快速转动的雨伞,飞出的水珠所在直线与圆相切,
2.在砂轮上打磨工件时,飞出的火星所在的轨迹与砂轮相切
3.打陀螺时,绳子与陀螺是相切的关系
思考:如图,如果直线l是⊙O 的切线,点A为切点,那么OA与直线l垂直吗?
A
l
O
探究二:切线的性质定理
结论:半径OA与直线l垂直
如何证明你的结论呢?
分析:直线l与半径OA的位置关系只有两种位置关系:要么直线l垂直于OA,要么直线l不垂直于OA,否定一个位置关系,肯定另一个位置关系成立。
证明:假设直线l不垂直于OA
过点O作OM⊥l (作垂线段)
∴ OM
这与条件直线l与⊙O相切相矛盾,顾假设不成立。
∴l⊥OA
切线的性质定理 :
圆的切线垂直于经过切点的半径.
∵直线l是⊙O 的切线,A是切点,
∴直线l ⊥OA.
A
l
O
几何语言:
例 已知:△ABC 为等腰三角形,O 是底边 BC 的中点,AB 与⊙O 相切于点 D.
求证: AC 是⊙O 的切线.
A
B
O
D
C
证明:如图,过点O作OE⊥AC,
垂足为E,连接OD,OA.
∵⊙O与AB相切于点D,
∴OD⊥AB.
又△ABC为等腰三角形,
O是底边BC的中点,
∴AO是∠BAC的平分线.
∴OE=OD,即OE是⊙O的半径.
∵AC经过⊙O的半径OE的外端E,并且垂直于半径OE
∴AC与⊙O相切.
A
B
O
D
C
E
证明:连接DO,
∵点D是BC的中点,
∴CD=BD.
∵AB是直径,
∴∠ADB=90°
∴AD⊥BC.
∴AC=AB
∴∠C=∠B.
随堂练习
1.如图,AB是⊙O的直径,⊙O交BC的中点于D,DE⊥AC于点E,连接AD,求证:DE是⊙O的切线.
∵OD=OB
∴∠B=∠ODB,
∴∠ODB=∠C
∴OD∥AC.
∵DE⊥AC,
∴∠ODE=∠CED=90°
∴DE⊥OD.
∴ED是⊙O的切线.
2.如图,在⊙O中,直径AB垂直于弦CD,垂足为E,连接AC,将△ACE沿AC翻折得到△ACF,直线FC与直线AB相交于点G.
(1)直线FC与⊙O有何位置关系?并说明理由;
(2)若OB=BG=2,求CD的长.
解:(1)直线FC与⊙O相切.
理由如下:连接OC.
∵OA=OC,
∴∠1=∠2.
由翻折,得∠1=∠3,∠F=∠AEC=90°.
∴∠2=∠3.
∴OC∥AF.
∴∠OCG=∠F=90°.
∴OC⊥FG.
∴直线FC与⊙O相切.
(2)∵直线GF与⊙O相切,
∴OC⊥FG.
∵OC=OB=BG,∴∠G=30°.
∴∠COG=60°,∴∠OCE=30°.
∴OE=1.∴CE= .
∵直径AB垂直于弦CD,
∴
课堂小结
1、切线的判定方法
2、切线的性质
(1)定义法
(2)数量关系法
(3)切线的判定定理
(1)切线的性质定理
(2)直线与圆只有1个公共点
(3)d=r
3、证切线时常用辅助线添加方法:
①有公共点,连半径,证垂直;
②无公共点,作垂直,证半径
同课章节目录
