2021-2022学年人教版数学 九年级上册第二十四章 圆24.1.4 圆周角课件(共58张PPT)
文档属性
| 名称 | 2021-2022学年人教版数学 九年级上册第二十四章 圆24.1.4 圆周角课件(共58张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 00:00:00 | ||
图片预览







文档简介
(共58张PPT)
人教版数学 九年级上册
第二十四章 圆
24.1 圆的有关性质
24.1.4 圆周角
问题1: 什么叫圆心角?指出图中的圆心角?
顶点在圆心的角叫圆心角, ∠BOC.
问题2: 如图,∠BAC的顶点和边有哪些特点
A
∠BAC的顶点在☉O上,角的两边分别交☉O于B、C两点.
导入新知
1. 理解圆周角的概念,会叙述并证明圆周角定理.
2. 掌握圆周角与圆心角的关系并能运用圆周角定理解决简单的几何问题.
3. 理解掌握圆周角定理的推论及其证明过程.
4. 掌握圆内接多边形的概念及圆内接四边形的性质并能运用其性质进行计算.
学习目标
顶点在圆上,并且两边都与圆相交的角叫做圆周角.
(两个条件必须同时具备,缺一不可)
新知一 圆周角的定义
合作探究
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
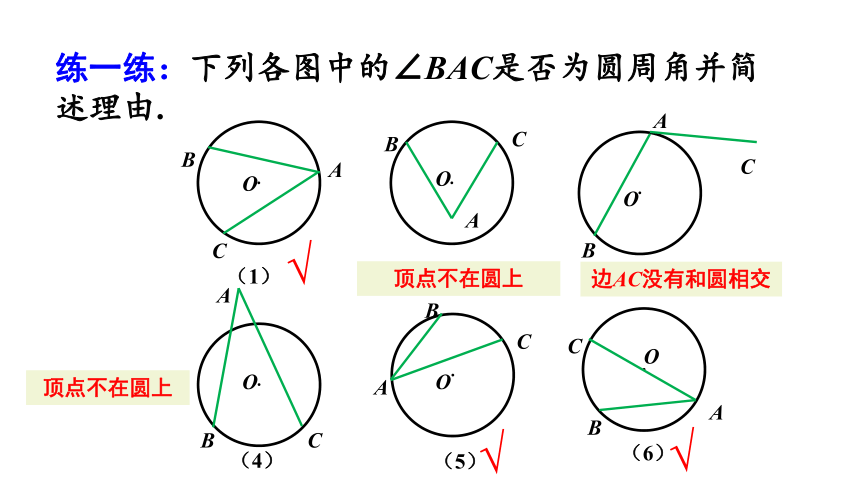
练一练:下列各图中的∠BAC是否为圆周角并简述理由.
(2)
(1)
(3)
(5)
(6)
顶点不在圆上
顶点不在圆上
边AC没有和圆相交
√
√
√
(4)
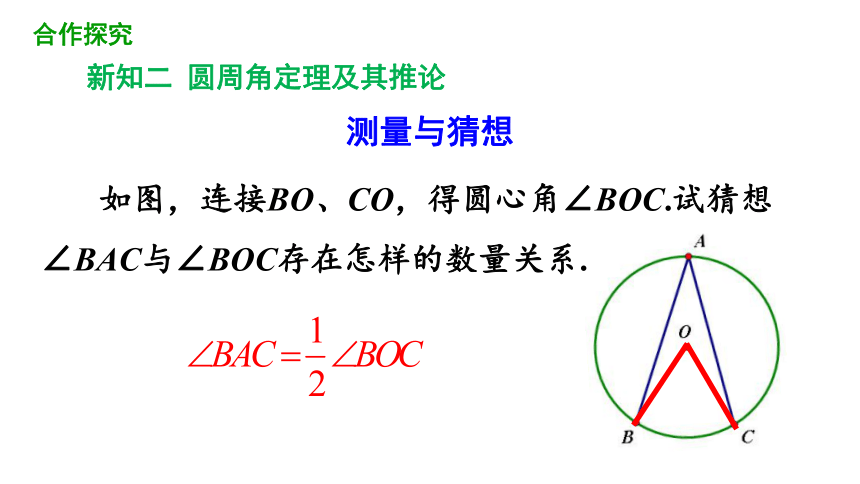
如图,连接BO、CO,得圆心角∠BOC.试猜想∠BAC与∠BOC存在怎样的数量关系.
新知二 圆周角定理及其推论
测量与猜想
合作探究
圆心O 在∠BAC 的 内部
圆心O在∠BAC的一边上
圆心O在∠BAC
的外部
推导与论证
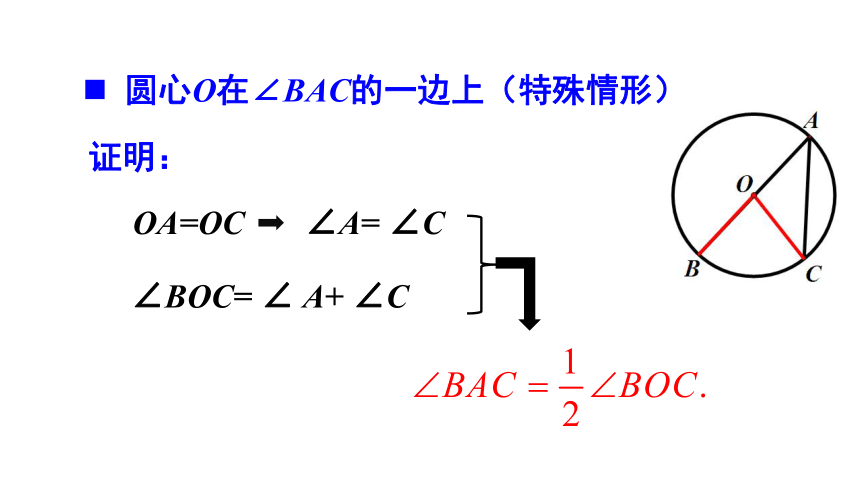
圆心O在∠BAC的一边上(特殊情形)
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
证明:
O
A
B
C
D
圆心O在∠BAC的内部
证明:连接AO并延长交⊙O于D.
B
C
O
A
D
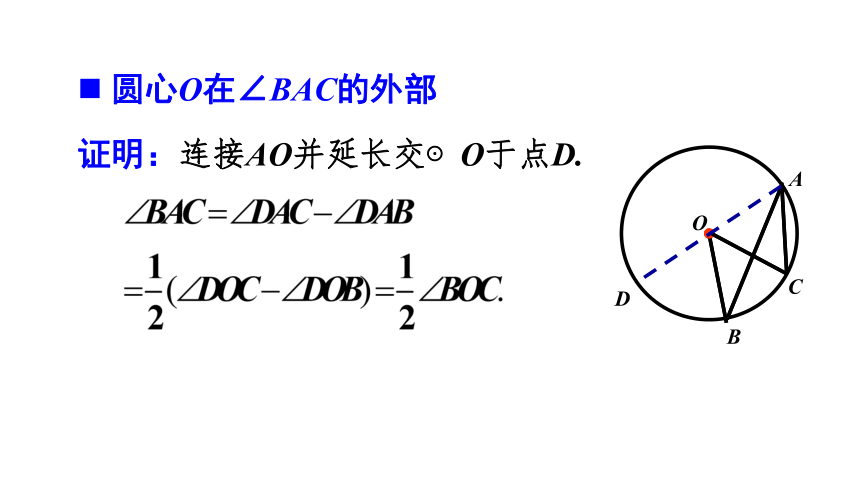
圆心O在∠BAC的外部
证明:连接AO并延长交⊙O于点D.
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半;
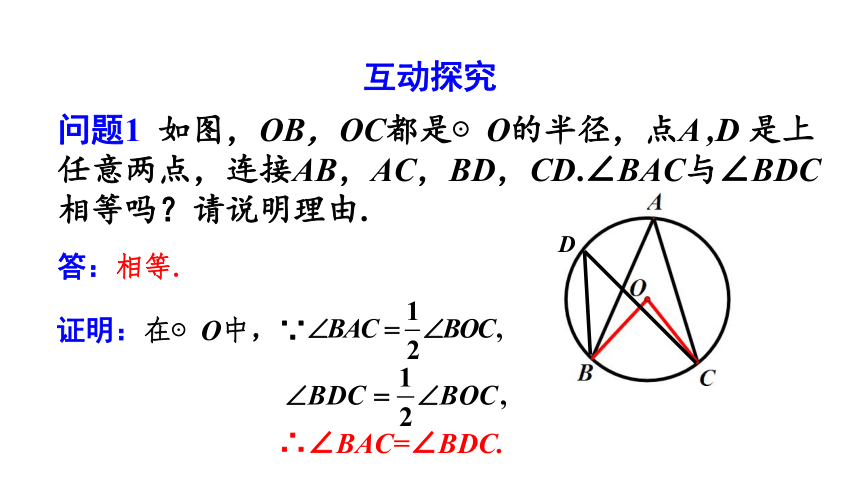
问题1 如图,OB,OC都是⊙O的半径,点A ,D 是上任意两点,连接AB,AC,BD,CD.∠BAC与∠BDC相等吗?请说明理由.
D
∴∠BAC=∠BDC.
答:相等.
证明:在⊙O中,∵
互动探究
D
A
B
O
C
E
F
问题2 如图,若 ∠A与∠B相等吗?
答:相等.
想一想:(1)反过来,若∠A=∠B,那么 成立吗?
(2)若CD是直径,你能求出∠A的度数吗?
证明:连接OC,OE,OD,OF
成立
90°
D
A
B
O
C
E
F
问题3 如图,若 ∠A与∠B相等吗?
答:相等.
证明:连接OC,OE,OD,OF,
∵
∴
∴
A1
A2
A3
圆周角定理的推论
同弧或等弧所对的圆周角相等.
试一试
如图,点A、B、C、D在☉O上,点A与点D在点B、C所在直线的同侧,∠BAC=35 .
(1)∠BOC= ,理由
是 ;
(2)∠BDC= ,理由是 .
70
35
同弧所对的圆周角相等
一条弧所对的圆周角等于它所对的圆心角的一半
如图,线段AB是☉O的直径,点C是 ☉O上的任意一点(除点A、B外),那么,∠ACB就是直径AB所对的圆周角,想一想,∠ACB会是怎样的角?
·
O
A
C
B
解:∵OA=OB=OC,
∴△AOC、△BOC都是等腰三角形.
∴ ∠OAC=∠OCA,∠OBC=∠OCB.
又∵ ∠OAC+∠OBC+∠ACB=180°.
∴ ∠ACB=∠OCA+∠OCB=180°÷2=90°.
圆周角和直径的关系
半圆或直径所对的圆周角是直角,
90°的圆周角所对的弦是直径.
例1 如图,AB是☉O的直径,∠A=80°.求∠ABC的大小.
O
C
A
B
解: ①∵AB是☉O的直径,
∴∠ACB=90°
∴∠ABC=180°-∠A-∠ACB
=180°-90°-80°=10°.
利用圆周角定理及推论求角的度数
典例精析
如图,AB是⊙O的直径,∠A=10°,
则∠ABC=______.
80°
巩固练习
例2 如图,分别求出图中∠x的大小.
60°
x
30°
20°
x
解:(1)∵同弧所对圆周角相等,∴∠x=60°.
A
D
B
E
C
(2)连接BF,
F
∵同弧所对圆周角相等,
∴∠ABF=∠D=20°,∠FBC=∠E=30°.
∴∠x=∠ABF+∠FBC=50°.
60°
x
A
B
D
C
典例精析
如图,正方形ABCD的顶点都在☉O上,P是弧DC上的一点,则∠BPC=_____.
45°
巩固练习
例3 如图,⊙O的直径AC为10cm,弦AD为6cm.
(1)求DC的长;
(2)若∠ADC的平分线交⊙O于B, 求AB、BC的长.
B
解:(1)∵AC是直径,
∴ ∠ADC=90°.
在Rt△ADC中,
利用圆周角定理及推论进行计算及证明线段相等
典例精析
在Rt△ABC中,AB2+BC2=AC2,
(2) ∵ AC是直径,
∴ ∠ABC=90°.
∵BD平分∠ADC,
∴∠ADB=∠CDB.
又∵∠ACB=∠ADB ,∠BAC=∠BDC .
∴ ∠BAC=∠ACB,
∴AB=BC.
B
∴
如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为( )
A.30° B.45° C.60° D.75°
C
巩固练习
如果一个多边形所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
新知三 圆内接四边形
合作探究
如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外接圆.
猜想:∠A与∠C, ∠B与∠D之间
的关系为:
∠A+ ∠C=180 ,
∠B+ ∠D=180 .
想一想:如何证明你的猜想呢?
探究性质
∵ 弧BCD和弧BAD所对的圆心角的和是周角,
∴∠A+∠C=180°,
同理∠B+∠D=180°,
推论:圆内接四边形的对角互补.
证明:
C
O
D
B
A
∵ 弧BCD和弧BAD所对的圆心角的和是周角,
∴∠A+∠C=180°,
同理∠B+∠D=180°,
E
∵∠BCD+∠DCE=180°.
∴∠A=∠DCE.
想一想:图中∠A与∠DCE的大小有何关系?
推论:圆的内接四边形的任何一个外角都等于它的内对角.
C
O
D
B
A
E
例 如图,AB为⊙O的直径,CF⊥AB于E,交⊙O于D,AF交⊙O于G. 求证:∠FGD=∠ADC.
证明:∵四边形ACDG内接于⊙O,
∴∠FGD=∠ACD.
又∵AB为⊙O的直径,CF⊥AB于E,
∴AB垂直平分CD,
∴AC=AD,
∴∠ADC=∠ACD,
∴∠FGD=∠ADC.
素养考点3
圆内接四边形性质的应用
典例精析
如图,在⊙O的内接四边形ABCD中,∠BOD=120°,那么∠BCD是( )
A.120° B.100°
C.80° D.60°
A
巩固练习
1.判断.
(1)同一个圆中等弧所对的圆周角相等( )
(2)相等的弦所对的圆周角也相等( )
(3)同弦所对的圆周角相等( )
√
×
×
课堂练习
2.已知△ABC的三个顶点在⊙O上,∠BAC=50°,
∠ABC=47°, 则∠AOB= .
B
A
C
O
166°
3. 如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为( )
A.30° B.40°
C.50° D.60°
A
A
B
C
D
O
4.如图,四边形ABCD内接于⊙O,如∠BOD=130°则∠BCD的度数是( )
A. 115° B. 130°
C. 65° D. 50°
C
A
O
B
C
∴∠ACB=2∠BAC.
证明:
5.如图,OA,OB,OC都是⊙O的半径,∠AOB=
2∠BOC. 求证:∠ACB=2∠BAC.
∠AOB=2∠BOC,
∵
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆周角定理的推论
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等
1.90°的圆周角所对的弦是直径;
2.圆内接四边形的对角互补
1.顶点在圆上,2.两边都与圆相交的角(二者必须同时具备)
圆周角与直
径的关系
半圆或直径所对的圆周角是直角
归纳新知
1.如图,点A,B,D在⊙O上,若∠BOD=130°,则∠BAD的度数是( )
A.50° B.60° C.65° D.80°
C
课后练习
B
3.如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=35°,则∠CAB的度数为( )
A.35° B.45° C.55° D.65°
C
B
5.如图,在⊙O中,CD⊥AB于点E,若∠B=60°,则∠A=_________.
30°
6.如图,⊙O的弦AB,CD的延长线相交于点P,且AB=CD.求证:PA=PC.
证明:如图,连接AC,
7.如图,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是( )
A.80° B.90° C.100° D.120°
D
8.(2020·镇江)如图,AB是半圆的直径,C,D是半圆上的两点,∠ADC=106°,则∠CAB等于( )
A.10° B.14° C.16° D.26°
C
D
10.(2020·陕西)如图,点A,B,C在⊙O上,BC∥OA,连接BO并延长,交⊙O于点D,连接AC,DC.若∠A=25°,则∠D的大小为( )
A.25° B.30° C.40° D.50°
C
D
12.如图,⊙C经过坐标原点,且与两坐标轴分别交于点A,B,点A的坐标为(0,4),M是圆上一点,∠BMO=120°.求⊙C的半径.
13.如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC,AC于点D,E,且点D为边BC的中点.
(1)求证:△ABC为等边三角形;
(2)求DE的长.
14.(教材P87例4变式)如图,已知四边形ADBC是⊙O的内接四边形,AB是直径,AB=10 cm,BC=8 cm,CD平分∠ACB.
(1)求AC与BD的长;
(2)求四边形ADBC的面积.
15.(2020·南京)如图,在△ABC中,AC=BC,D是AB上一点,⊙O经过点A,C,D,交BC于点E,过点D作DF∥BC,交⊙O于点F.求证:
(1)四边形DBCF是平行四边形;
(2)AF=EF.
证明:(1)∵AC=BC,∴∠BAC=∠B,∵DF∥BC,∴∠ADF=∠B,∵∠BAC=∠CFD,∴∠ADF=∠CFD,∴BD∥CF,∵DF∥BC,∴四边形DBCF是平行四边形
(2)如图,连接AE,∵∠ADF=∠B,∠ADF=∠AEF,∴∠AEF=∠B,∵四边形AECF是⊙O的内接四边形,∴∠ECF+∠EAF=180°,∵BD∥CF,∴∠ECF+∠B=180°,∴∠EAF=∠B,∴∠AEF=∠EAF,∴AF=EF
再 见
人教版数学 九年级上册
第二十四章 圆
24.1 圆的有关性质
24.1.4 圆周角
问题1: 什么叫圆心角?指出图中的圆心角?
顶点在圆心的角叫圆心角, ∠BOC.
问题2: 如图,∠BAC的顶点和边有哪些特点
A
∠BAC的顶点在☉O上,角的两边分别交☉O于B、C两点.
导入新知
1. 理解圆周角的概念,会叙述并证明圆周角定理.
2. 掌握圆周角与圆心角的关系并能运用圆周角定理解决简单的几何问题.
3. 理解掌握圆周角定理的推论及其证明过程.
4. 掌握圆内接多边形的概念及圆内接四边形的性质并能运用其性质进行计算.
学习目标
顶点在圆上,并且两边都与圆相交的角叫做圆周角.
(两个条件必须同时具备,缺一不可)
新知一 圆周角的定义
合作探究
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
·
C
O
A
B
·
C
O
B
·
C
O
B
A
A
练一练:下列各图中的∠BAC是否为圆周角并简述理由.
(2)
(1)
(3)
(5)
(6)
顶点不在圆上
顶点不在圆上
边AC没有和圆相交
√
√
√
(4)
如图,连接BO、CO,得圆心角∠BOC.试猜想∠BAC与∠BOC存在怎样的数量关系.
新知二 圆周角定理及其推论
测量与猜想
合作探究
圆心O 在∠BAC 的 内部
圆心O在∠BAC的一边上
圆心O在∠BAC
的外部
推导与论证
圆心O在∠BAC的一边上(特殊情形)
OA=OC
∠A= ∠C
∠BOC= ∠ A+ ∠C
证明:
O
A
B
C
D
圆心O在∠BAC的内部
证明:连接AO并延长交⊙O于D.
B
C
O
A
D
圆心O在∠BAC的外部
证明:连接AO并延长交⊙O于点D.
圆周角定理
一条弧所对的圆周角等于它所对的圆心角的一半;
问题1 如图,OB,OC都是⊙O的半径,点A ,D 是上任意两点,连接AB,AC,BD,CD.∠BAC与∠BDC相等吗?请说明理由.
D
∴∠BAC=∠BDC.
答:相等.
证明:在⊙O中,∵
互动探究
D
A
B
O
C
E
F
问题2 如图,若 ∠A与∠B相等吗?
答:相等.
想一想:(1)反过来,若∠A=∠B,那么 成立吗?
(2)若CD是直径,你能求出∠A的度数吗?
证明:连接OC,OE,OD,OF
成立
90°
D
A
B
O
C
E
F
问题3 如图,若 ∠A与∠B相等吗?
答:相等.
证明:连接OC,OE,OD,OF,
∵
∴
∴
A1
A2
A3
圆周角定理的推论
同弧或等弧所对的圆周角相等.
试一试
如图,点A、B、C、D在☉O上,点A与点D在点B、C所在直线的同侧,∠BAC=35 .
(1)∠BOC= ,理由
是 ;
(2)∠BDC= ,理由是 .
70
35
同弧所对的圆周角相等
一条弧所对的圆周角等于它所对的圆心角的一半
如图,线段AB是☉O的直径,点C是 ☉O上的任意一点(除点A、B外),那么,∠ACB就是直径AB所对的圆周角,想一想,∠ACB会是怎样的角?
·
O
A
C
B
解:∵OA=OB=OC,
∴△AOC、△BOC都是等腰三角形.
∴ ∠OAC=∠OCA,∠OBC=∠OCB.
又∵ ∠OAC+∠OBC+∠ACB=180°.
∴ ∠ACB=∠OCA+∠OCB=180°÷2=90°.
圆周角和直径的关系
半圆或直径所对的圆周角是直角,
90°的圆周角所对的弦是直径.
例1 如图,AB是☉O的直径,∠A=80°.求∠ABC的大小.
O
C
A
B
解: ①∵AB是☉O的直径,
∴∠ACB=90°
∴∠ABC=180°-∠A-∠ACB
=180°-90°-80°=10°.
利用圆周角定理及推论求角的度数
典例精析
如图,AB是⊙O的直径,∠A=10°,
则∠ABC=______.
80°
巩固练习
例2 如图,分别求出图中∠x的大小.
60°
x
30°
20°
x
解:(1)∵同弧所对圆周角相等,∴∠x=60°.
A
D
B
E
C
(2)连接BF,
F
∵同弧所对圆周角相等,
∴∠ABF=∠D=20°,∠FBC=∠E=30°.
∴∠x=∠ABF+∠FBC=50°.
60°
x
A
B
D
C
典例精析
如图,正方形ABCD的顶点都在☉O上,P是弧DC上的一点,则∠BPC=_____.
45°
巩固练习
例3 如图,⊙O的直径AC为10cm,弦AD为6cm.
(1)求DC的长;
(2)若∠ADC的平分线交⊙O于B, 求AB、BC的长.
B
解:(1)∵AC是直径,
∴ ∠ADC=90°.
在Rt△ADC中,
利用圆周角定理及推论进行计算及证明线段相等
典例精析
在Rt△ABC中,AB2+BC2=AC2,
(2) ∵ AC是直径,
∴ ∠ABC=90°.
∵BD平分∠ADC,
∴∠ADB=∠CDB.
又∵∠ACB=∠ADB ,∠BAC=∠BDC .
∴ ∠BAC=∠ACB,
∴AB=BC.
B
∴
如图,BD是⊙O的直径,∠CBD=30°,则∠A的度数为( )
A.30° B.45° C.60° D.75°
C
巩固练习
如果一个多边形所有顶点都在同一个圆上,这个多边形叫做圆内接多边形,这个圆叫做这个多边形的外接圆.
新知三 圆内接四边形
合作探究
如图,四边形ABCD为⊙O的内接四边形,⊙O为四边形ABCD的外接圆.
猜想:∠A与∠C, ∠B与∠D之间
的关系为:
∠A+ ∠C=180 ,
∠B+ ∠D=180 .
想一想:如何证明你的猜想呢?
探究性质
∵ 弧BCD和弧BAD所对的圆心角的和是周角,
∴∠A+∠C=180°,
同理∠B+∠D=180°,
推论:圆内接四边形的对角互补.
证明:
C
O
D
B
A
∵ 弧BCD和弧BAD所对的圆心角的和是周角,
∴∠A+∠C=180°,
同理∠B+∠D=180°,
E
∵∠BCD+∠DCE=180°.
∴∠A=∠DCE.
想一想:图中∠A与∠DCE的大小有何关系?
推论:圆的内接四边形的任何一个外角都等于它的内对角.
C
O
D
B
A
E
例 如图,AB为⊙O的直径,CF⊥AB于E,交⊙O于D,AF交⊙O于G. 求证:∠FGD=∠ADC.
证明:∵四边形ACDG内接于⊙O,
∴∠FGD=∠ACD.
又∵AB为⊙O的直径,CF⊥AB于E,
∴AB垂直平分CD,
∴AC=AD,
∴∠ADC=∠ACD,
∴∠FGD=∠ADC.
素养考点3
圆内接四边形性质的应用
典例精析
如图,在⊙O的内接四边形ABCD中,∠BOD=120°,那么∠BCD是( )
A.120° B.100°
C.80° D.60°
A
巩固练习
1.判断.
(1)同一个圆中等弧所对的圆周角相等( )
(2)相等的弦所对的圆周角也相等( )
(3)同弦所对的圆周角相等( )
√
×
×
课堂练习
2.已知△ABC的三个顶点在⊙O上,∠BAC=50°,
∠ABC=47°, 则∠AOB= .
B
A
C
O
166°
3. 如图,已知BD是⊙O的直径,⊙O的弦AC⊥BD于点E,若∠AOD=60°,则∠DBC的度数为( )
A.30° B.40°
C.50° D.60°
A
A
B
C
D
O
4.如图,四边形ABCD内接于⊙O,如∠BOD=130°则∠BCD的度数是( )
A. 115° B. 130°
C. 65° D. 50°
C
A
O
B
C
∴∠ACB=2∠BAC.
证明:
5.如图,OA,OB,OC都是⊙O的半径,∠AOB=
2∠BOC. 求证:∠ACB=2∠BAC.
∠AOB=2∠BOC,
∵
圆心角
类比
圆周角
圆周角定义
圆周角定理
圆周角定理的推论
在同圆或等圆中,同弧或等弧所对的圆周角相等,都等于该弧所对的圆心角的一半;相等的圆周角所对的弧相等
1.90°的圆周角所对的弦是直径;
2.圆内接四边形的对角互补
1.顶点在圆上,2.两边都与圆相交的角(二者必须同时具备)
圆周角与直
径的关系
半圆或直径所对的圆周角是直角
归纳新知
1.如图,点A,B,D在⊙O上,若∠BOD=130°,则∠BAD的度数是( )
A.50° B.60° C.65° D.80°
C
课后练习
B
3.如图,AB为⊙O的直径,CD是⊙O的弦,∠ADC=35°,则∠CAB的度数为( )
A.35° B.45° C.55° D.65°
C
B
5.如图,在⊙O中,CD⊥AB于点E,若∠B=60°,则∠A=_________.
30°
6.如图,⊙O的弦AB,CD的延长线相交于点P,且AB=CD.求证:PA=PC.
证明:如图,连接AC,
7.如图,四边形ABCD为⊙O的内接四边形,∠BCD=120°,则∠BOD的大小是( )
A.80° B.90° C.100° D.120°
D
8.(2020·镇江)如图,AB是半圆的直径,C,D是半圆上的两点,∠ADC=106°,则∠CAB等于( )
A.10° B.14° C.16° D.26°
C
D
10.(2020·陕西)如图,点A,B,C在⊙O上,BC∥OA,连接BO并延长,交⊙O于点D,连接AC,DC.若∠A=25°,则∠D的大小为( )
A.25° B.30° C.40° D.50°
C
D
12.如图,⊙C经过坐标原点,且与两坐标轴分别交于点A,B,点A的坐标为(0,4),M是圆上一点,∠BMO=120°.求⊙C的半径.
13.如图,在△ABC中,AB=BC=2,以AB为直径的⊙O分别交BC,AC于点D,E,且点D为边BC的中点.
(1)求证:△ABC为等边三角形;
(2)求DE的长.
14.(教材P87例4变式)如图,已知四边形ADBC是⊙O的内接四边形,AB是直径,AB=10 cm,BC=8 cm,CD平分∠ACB.
(1)求AC与BD的长;
(2)求四边形ADBC的面积.
15.(2020·南京)如图,在△ABC中,AC=BC,D是AB上一点,⊙O经过点A,C,D,交BC于点E,过点D作DF∥BC,交⊙O于点F.求证:
(1)四边形DBCF是平行四边形;
(2)AF=EF.
证明:(1)∵AC=BC,∴∠BAC=∠B,∵DF∥BC,∴∠ADF=∠B,∵∠BAC=∠CFD,∴∠ADF=∠CFD,∴BD∥CF,∵DF∥BC,∴四边形DBCF是平行四边形
(2)如图,连接AE,∵∠ADF=∠B,∠ADF=∠AEF,∴∠AEF=∠B,∵四边形AECF是⊙O的内接四边形,∴∠ECF+∠EAF=180°,∵BD∥CF,∴∠ECF+∠B=180°,∴∠EAF=∠B,∴∠AEF=∠EAF,∴AF=EF
再 见
同课章节目录
