人教版九年级上册数学第二十二章 二次函数22.3实际问题与二次函数--拱桥问题训练(word版含答案)
文档属性
| 名称 | 人教版九年级上册数学第二十二章 二次函数22.3实际问题与二次函数--拱桥问题训练(word版含答案) | 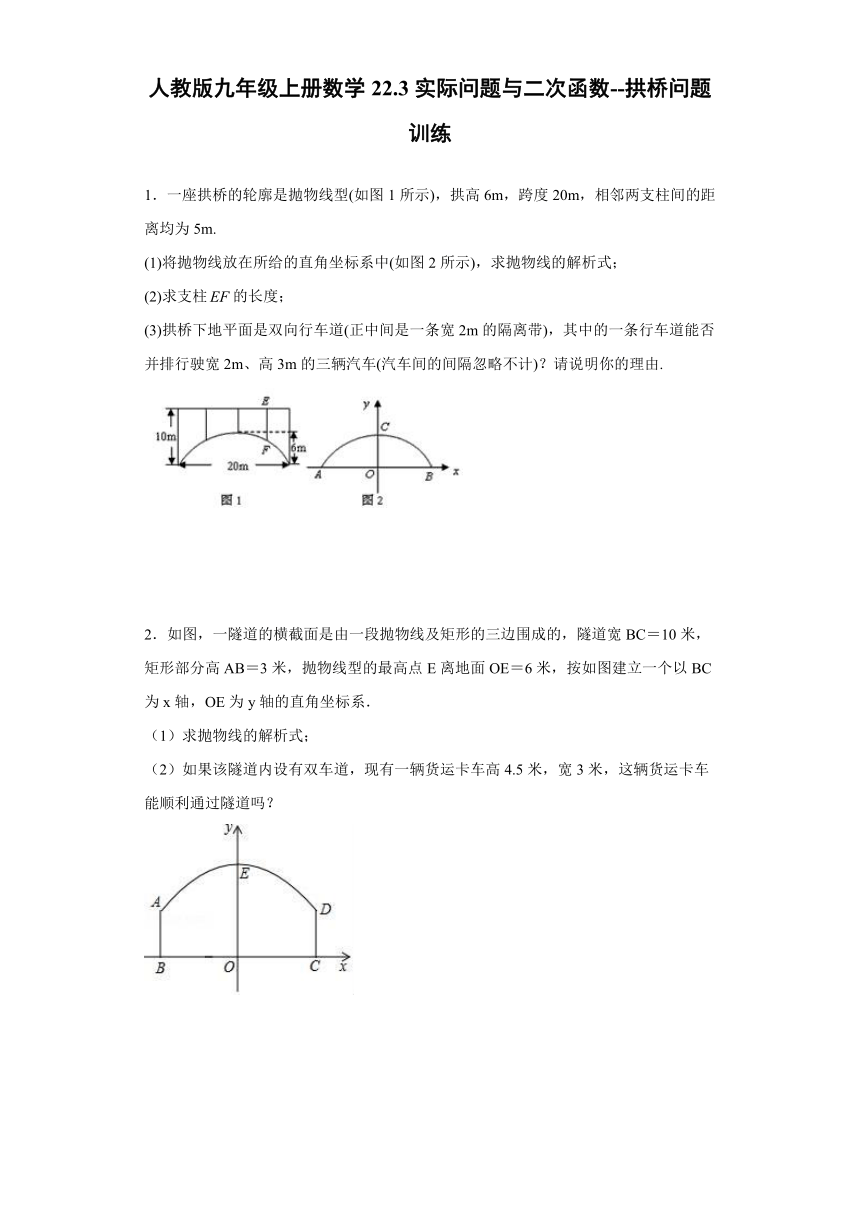 | |
| 格式 | doc | ||
| 文件大小 | 620.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 09:59:41 | ||
图片预览




文档简介
人教版九年级上册数学22.3实际问题与二次函数--拱桥问题训练
1.一座拱桥的轮廓是抛物线型(如图1所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.
(1)将抛物线放在所给的直角坐标系中(如图2所示),求抛物线的解析式;
(2)求支柱的长度;
(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说明你的理由.
2.如图,一隧道的横截面是由一段抛物线及矩形的三边围成的,隧道宽BC=10米,矩形部分高AB=3米,抛物线型的最高点E离地面OE=6米,按如图建立一个以BC为x轴,OE为y轴的直角坐标系.
(1)求抛物线的解析式;
(2)如果该隧道内设有双车道,现有一辆货运卡车高4.5米,宽3米,这辆货运卡车能顺利通过隧道吗?
3.如图,隧道的截面由抛物线和长方形构成.长方形的长是,宽是,抛物线可以用表示.
一辆货运卡车高,宽,它能通过该隧道吗?
如果该隧道内设双行道,那么这辆货运卡车是否可以通过?
4.建立适当的坐标系,运用函数知识解决下面的问题:
如图,是某条河上的一座抛物线形拱桥,拱桥顶部点E到桥下水面的距离EF为3米时,水面宽AB为6米,一场大雨过后,河水上涨,水面宽度变为CD,且CD=2米,此时水位上升了多少米?
5.如图所示,有一座抛物线形拱桥,桥下面在正常水位时,AB宽20 m,水位上升到警戒线CD时,CD到拱桥顶E的距离仅为1 m,这时水面宽度为10 m.
(1)在如图所示的坐标系中求抛物线的解析式;
(2)若洪水到来时,水位以每小时0.3 m的速度上升,从正常水位开始,持续多少小时到达警戒线?
6.如图所示的是水面一桥拱的示意图,它的形状类似于抛物线,在正常水位时,该桥下水面宽度为20米,拱顶距离正常水面4米,建立平面直角坐标系如图所示,求抛物线的解析式.
7.如图,东湖隧道的截面由抛物线和长方形构成,长方形的长OA为12 m,宽OB为4 m,隧道顶端D到路面的距离为10 m,建立如图所示的直角坐标系.
(1)求该抛物线的表达式;
(2)一辆货车载有一个长方体集装箱,集装箱最高处与地面距离为6 m,宽为4 m,隧道内设双向行车道,问这辆货车能否安全通过?
(3)在抛物线形拱壁上需要安装两排离地面高度相等的灯,如果灯离地面的高度不超过8.5 m,那么这两排灯的水平距离最小是多少米?
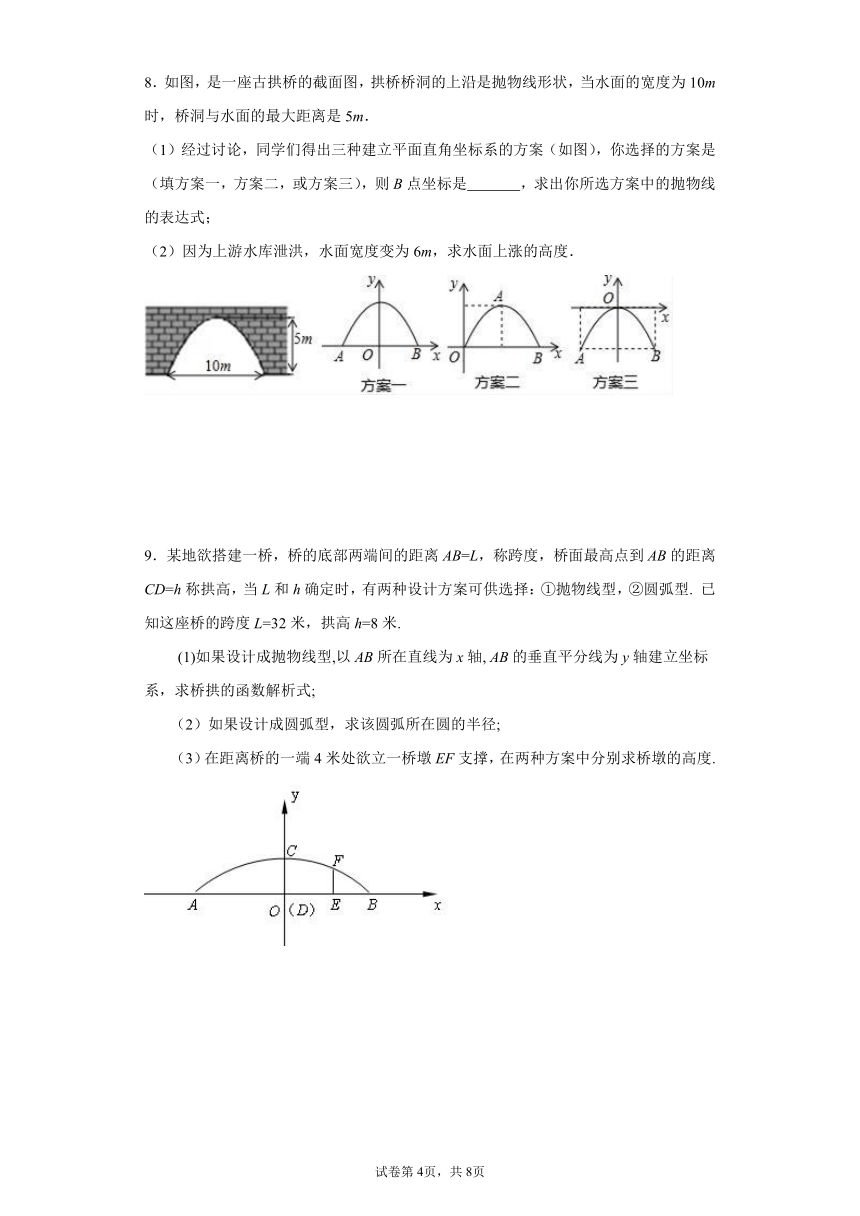
8.如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面的最大距离是5m.
(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如图),你选择的方案是 (填方案一,方案二,或方案三),则B点坐标是 ,求出你所选方案中的抛物线的表达式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.
9.某地欲搭建一桥,桥的底部两端间的距离AB=L,称跨度,桥面最高点到AB的距离CD=h称拱高,当L和h确定时,有两种设计方案可供选择:①抛物线型,②圆弧型. 已知这座桥的跨度L=32米,拱高h=8米.
(1)如果设计成抛物线型,以AB所在直线为x轴, AB的垂直平分线为y轴建立坐标系,求桥拱的函数解析式;
(2)如果设计成圆弧型,求该圆弧所在圆的半径;
(3)在距离桥的一端4米处欲立一桥墩EF支撑,在两种方案中分别求桥墩的高度.
10.某菜农搭建了一个横截面为抛物线的大棚,尺寸如图:
(1)如图建立平面直角坐标系,使抛物线对称轴为y轴,求该抛物线的解析式;
(2)若需要开一个截面为矩形的门(如图所示),已知门的高度为1.60米,那么门的宽度最大是多少米(不考虑材料厚度) (结果保留根号)
11.如图,是一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是,拱桥的跨度为,桥洞与水面的最大距离是,桥洞两侧壁上各有一盏距离水面的景观灯,把拱桥的截面图放在平面直角坐标系中.
(1)求抛物线对应的函数解析式,并写出自变量的取值范围;
(2)求两盏景观灯之间的水平距离.
12.如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE、ED、DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的距离是11m,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
(1)求抛物线的解析式;
(2)已知从某时刻开始的40h内,水面与河底ED的距离h(单位:m)随时间t(单位:h)的变化满足函数关系h=-(t-19)2+8(0≤t≤40)且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
13.施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系(如图1所示).
(1)求出这条抛物线的函数解析式,并写出自变量x的取值范围;
(2)隧道下的公路是双向行车道(正中间是一条宽1米的隔离带),其中的一条行车道能否行驶宽2.5米、高5米的特种车辆?请通过计算说明;
(3)施工队计划在隧道门口搭建一个矩形脚手架CDAB,使A、D点在抛物线上.B、C点在地面OM线上(如图2所示).为了筹备材料,需测算“脚手架”三根钢杆AB、AD、DC的长度之和的最大值是多少,请你帮施工队计算一下.
14.有一个抛物线形的桥洞,桥洞离水面的最大高度BM为3米,跨度OA为6米,以OA所在直线为x轴,O为原点建立直角坐标系(如图所示).
(1)请你直接写出O、A、M三点的坐标;
(2)一艘小船平放着一些长3米,宽2米且厚度均匀的矩形木板,要使该小船能通过此桥洞,问这些木板最高可堆放多少米(设船身底板与水面同一平面)?
15.一隧道内设双行公路,隧道的高MN为6米.下图是隧道的截面示意图,并建立如图所示的直角坐标系,它是由一段抛物线和一个矩形CDEF的三条边围成的,矩形的长DE是8米,宽CD是2米.
(1)求该抛物线的解析式;
(2)为了保证安全,要求行驶的车辆顶部与隧道顶部至少要有0.5米的距离.若行车道总宽度PQ(居中,两边为人行道)为6米,一辆高3.2米的货运卡车(设为长方形)靠近最右边行驶能否安全?请写出判断过程;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABHG,使H、G两点在抛物线上,A、B两点在地面DE上,设GH长为n米,“脚手架”三根木杆AG、GH、HB的长度之和为L,当n为何值时L最大,最大值为多少?
16.某工厂大门是一抛物线水泥建筑物(如图),大门地面宽AB=4 m,顶部C离地面高为4.4 m.
(1)以AB所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,求该抛物线对应的函数表达式;
(2)现有一辆载满货物的汽车欲通过大门,货物顶点距地面2.8 m,装货宽度为2.4 m,请通过计算,判断这辆汽车能否顺利通过大门.
17.某涵洞是抛物线形,它的截面如图所示,现测得水面宽AB=1.6m,涵洞顶点O到水面的距离为2.4m,在图中直角坐标系内,求涵洞所在抛物线的函数表达式.
18.如图:河上有一座抛物线形桥洞,已知桥下的水面离桥拱顶部3m时,水面宽AB=6m,建立如图所示的坐标系.
(1)当水位上升0.5m时,求水面宽度CD为多少米?(结果可保留根号)
(2)有一艘游船它的左右两边缘最宽处有一个长方体形状的遮阳棚,此船正对着桥洞在上述河流中航行,若这船宽(最大宽度)2米,从水面到棚顶高度为1.8米.问这艘船能否从桥下洞通过?
参考答案
1.
解:(1)根据题目条件,A、B、C的坐标分别是(-10,0)、(10,0)、(0,6).
设抛物线的解析式为y=ax2+c,
将B、C的坐标代入y=ax2+c,得
解得a=,c=6.
所以抛物线的表达式是y=x2+6.
(2)可设,于是,
从而支柱EF的长度是10-4.5=5.5米.
(3)设DN是隔离带的宽,NG是三辆车的宽度和,则G点坐标是.
过G点作GH垂直AB交抛物线于H,则.
根据抛物线的特点,可知一条行车道能并排行驶这样的三辆汽车.
2.
(1)设抛物线的解析式为y=ax2+c.
∵点E(0,6),点A(﹣5,3)在此抛物线上,∴,得:,∴此抛物线的解析式为y6;
(2)当x=±3时,y6=4.92>4.5,即这辆货运卡车能顺利通过隧道.
3.
解:把代入得:
,
解得,
∴此时可通过物体的宽度为,
∴能通过;
∵一辆货运卡车高,隧道的截面由抛物线和长方形构成.长方形的长是,宽是,
∴货车上面有,在矩形上面,当时,
,
解得,
∵,
∴能通过.
4.
以点E为原点、EF所在直线为y轴,垂直EF的直线为x轴建立平面直角坐标系,
根据题意知E(0,0)、A(﹣3,﹣3)、B(3,﹣3),
设y=kx2(k<0),
将点(3,﹣3)代入,得:k=﹣,
∴y=﹣x2,
将x=代入,得:y=﹣2,
∴上升了1米.
5.
解:(1)设所求抛物线的解析式为y=ax2.
∵CD=10 m,CD到拱桥顶E的距离仅为1 m,
∴C(-5,-1).
把点C的坐标代入y=ax2,
得a=-,
故抛物线的解析式为y=-x2.
(2)∵AB宽20 m,
∴可设A(-10,b).
把点A的坐标代入抛物线的解析式y=-x2中,
解得b=-4,
∴点A的坐标为(-10,-4).
设AB与y轴交于点F,则F(0,-4),
∴EF=3 m.
∵水位以每小时0.3 m的速度上升,
∴3÷0.3=10(时).
答:从正常水位开始,持续10小时到达警戒线.
6.
试题解析:设抛物线解析式为
把点代入解析式得:
解得:
∴抛物线的解析式为
7.
试题分析:(1)设出抛物线的解析式,根据抛物线顶点坐标,代入解析式;
(2)令x=10,求出y与6作比较;
(3)求出y=8.5时x的值即可得.
试题解析:(1)根据题意,该抛物线的顶点坐标为(6,10),
设抛物线解析式为:y=+10,
将点B(0,4)代入,得:36a+10=4,
解得:a=,
故该抛物线解析式为y=+10;
(2)根据题意,当x=6+4=10时,y=×16+10=>6,
∴这辆货车能安全通过.
(3)当y=8.5时,有:+10=8.5,
解得:=3,=9,
∴﹣=6,
答:两排灯的水平距离最小是6米.
考点:二次函数的应用.
8.
:解:方案1:(1)点B的坐标为(5,0),设抛物线的解析式为:.由题意可以得到抛物线的顶点为(0,5),代入解析式可得:,∴抛物线的解析式为:;
(2)由题意:把代入,解得:=3.2,∴水面上涨的高度为3.2m.
方案2:(1)点B的坐标为(10,0).设抛物线的解析式为:.
由题意可以得到抛物线的顶点为(5,5),代入解析式可得:,∴抛物线的解析式为:;
(2)由题意:把代入解得:=3.2,∴水面上涨的高度为3.2m.
方案3:(1)点B的坐标为(5, ),由题意可以得到抛物线的顶点为(0,0).
设抛物线的解析式为:,把点B的坐标(5, ),代入解析式可得:,
∴抛物线的解析式为:;
(2)由题意:把代入解得:=,∴水面上涨的高度为3.2m.
9.
解析:(1)抛物线的解析式为y=ax2+c,
又∵抛物线经过点C(0,8)和点B(16,0),
∴0=256a+8,a=-.
∴抛物线的解析式为y=-x2+8(-16≤x≤16);
(2)设弧AB所在的圆心为O,C为弧AB的中点,CD⊥AB于D,延长CD经过O点,
设⊙O的半径为R,
在Rt△OBD中,OB2=OD2+DB2
∴R2=(R-8)2+162,解得R=20;
(3)①在抛物线型中设点F(x,y)在抛物线上,x=OE=16-4=12,
EF=y=3.5米;
②在圆弧型中设点F′在弧AB上,作F′E′⊥AB于E′,
OH⊥F′E′于H,则OH=D E′=16-4=12,O F′=R=20,
在Rt△OH F′中,H F′= ,
∵HE′=OD=OC-CD=20-8=12,E′F′=HF′-HE′=16-12=4(米)
∴在离桥的一端4米处,抛物线型桥墩高3.5米; 圆弧型桥墩高4米.
10.
解:(1)由图可设抛物线的解析式为:y=ax2+2,
由图知抛物线与x轴正半轴的交点为(2,0),则:a×22+2=0,
∴a=﹣,
∴抛物线的解析式为y=﹣x2+2;
(2)当y=1.60时,知1.6=﹣x2+2,
解得:x=,
所以门的宽度最大为2×=米.
考点:二次函数的应用.
11.
(1)抛物线的顶点坐标为(5,5),与y轴交点坐标是(0,1),设抛物线的解析式是y=a(x﹣5)2+5,把(0,1)代入y=a(x﹣5)2+5,得:a=﹣,∴y=﹣(x﹣5)2+5(0≤x≤10),即(0≤x≤10);
(2)由已知得两景观灯的纵坐标都是4,∴4=﹣(x﹣5)2+5,∴(x﹣5)2=1,∴x1=,x2=,∴两景观灯间的距离为 ﹣=5米.
12.
二次函数的应用,待定系数法,曲线上点的坐标与方程的关系.
(1)根据抛物线特点设出二次函数解析式,把B坐标代入即可求解.
(2)水面到顶点C的距离不大于5米时,即水面与河底ED的距离h至多为6,把6代入所给二次函数关系式,求得t的值,相减即可得到禁止船只通行的时间.
13.
(1)∵M(12,0),P(6,6).
∴设这条抛物线的函数解析式为y=a(x-6)2+6,
∵把(0,0)代入解得a=-,
∴这条抛物线的函数解析式为y=-(x-6)2+6,
即y=-x2+2x(0≤x≤12);
(2)当x=6-0.5-2.5=3(或x=6+0.5+2.5=9)时,y=4.5<5
∴不能行驶宽2.5米、高5米的特种车辆;
(3)设点A的坐标为(m,-m2+2m),
∴OB=m,AB=DC=-m2+2m
根据抛物线的轴对称可得OB=CM=m,
∴BC=12-2m,即AD=12-2m
∴L=AB+AD+DC=-m2+2m+12=-(m-3)2+15
∴当m=3,即OB=3米时,三根木杆长度之和L的最大值为15米.
14.
解:(1)0(0,0),A(6,0),M(3,3).
(2)设抛物线的关系式为y=a(x-3)2+3,
因为抛物线过点(0,0),
所以0=a(0-3)2+3,
解得a=,
所以,
要使木板堆放最高,依据题意,得B点应是木板宽CD的中点,
把x=2代入,
得,所以这些木板最高可堆放米.
15.
解:(1)由题意得M(0,4),F(4,0)
可设抛物线的解析式为y=ax2+4,
将F(4,0)代入y=ax2+4中,得a=-,
∴抛物线的解析式为y=-x2+4;
(2)当x=3,y=,
+2-=3.253.2,∴能安全通过;
(3)由GH=n,可设H(),
∴GH+GA+BH=n+()×2+2×2=,
∴L=,
∵a<0,抛物线开口向下,
∴当n=-=4时,L有最大值,最大值为14.
16.
解:(1)如图,过AB的中点作AB的垂直平分线,建立平面直角坐标系.点A,B,C的坐标分别为 A(-2,0),B(2,0),C(0,4.4).
设抛物线的表达式为y=a(x-2)(x+2).
将点C(0,4.4)代入得
a(0-2)(0+2)=4.4,解得a=-1.1,
∴y=-1.1(x-2)(x+2)=-1.1x2+4.4.
故此抛物线的表达式为y=-1.1x2+4.4.
(2)∵货物顶点距地面2.8 m,装货宽度为2.4,
∴只要判断点(-1.2,2.8)或点(1.2,2.8)与抛物线的位置关系即可.
将x=1.2代入抛物线,得 y=2.816>2.8,
∴点(-1.2,2.8)和点(1.2,2.8)都在抛物线内.
∴这辆汽车能够通过大门.
17.
解:设此抛物线所对应的函数表达式为:,
∵,涵洞顶点到水面的距离为,
∴点坐标应该是,
把点代入得:,
解得:,
故涵洞所在抛物线的函数表达式.
18.
(1)设抛物线形桥洞的函数解析式为y=ax2+c,
把A(3,0),E(0,3)代入得:
解得:
∴
由题意得:点C与D的纵坐标为0.5,
∴
解得:
∴(米),
则水面的宽度CD为米;
(2)当x=1时,
∵
∴这艘游船能从桥洞下通过.
试卷第2页,共8页
1.一座拱桥的轮廓是抛物线型(如图1所示),拱高6m,跨度20m,相邻两支柱间的距离均为5m.
(1)将抛物线放在所给的直角坐标系中(如图2所示),求抛物线的解析式;
(2)求支柱的长度;
(3)拱桥下地平面是双向行车道(正中间是一条宽2m的隔离带),其中的一条行车道能否并排行驶宽2m、高3m的三辆汽车(汽车间的间隔忽略不计)?请说明你的理由.
2.如图,一隧道的横截面是由一段抛物线及矩形的三边围成的,隧道宽BC=10米,矩形部分高AB=3米,抛物线型的最高点E离地面OE=6米,按如图建立一个以BC为x轴,OE为y轴的直角坐标系.
(1)求抛物线的解析式;
(2)如果该隧道内设有双车道,现有一辆货运卡车高4.5米,宽3米,这辆货运卡车能顺利通过隧道吗?
3.如图,隧道的截面由抛物线和长方形构成.长方形的长是,宽是,抛物线可以用表示.
一辆货运卡车高,宽,它能通过该隧道吗?
如果该隧道内设双行道,那么这辆货运卡车是否可以通过?
4.建立适当的坐标系,运用函数知识解决下面的问题:
如图,是某条河上的一座抛物线形拱桥,拱桥顶部点E到桥下水面的距离EF为3米时,水面宽AB为6米,一场大雨过后,河水上涨,水面宽度变为CD,且CD=2米,此时水位上升了多少米?
5.如图所示,有一座抛物线形拱桥,桥下面在正常水位时,AB宽20 m,水位上升到警戒线CD时,CD到拱桥顶E的距离仅为1 m,这时水面宽度为10 m.
(1)在如图所示的坐标系中求抛物线的解析式;
(2)若洪水到来时,水位以每小时0.3 m的速度上升,从正常水位开始,持续多少小时到达警戒线?
6.如图所示的是水面一桥拱的示意图,它的形状类似于抛物线,在正常水位时,该桥下水面宽度为20米,拱顶距离正常水面4米,建立平面直角坐标系如图所示,求抛物线的解析式.
7.如图,东湖隧道的截面由抛物线和长方形构成,长方形的长OA为12 m,宽OB为4 m,隧道顶端D到路面的距离为10 m,建立如图所示的直角坐标系.
(1)求该抛物线的表达式;
(2)一辆货车载有一个长方体集装箱,集装箱最高处与地面距离为6 m,宽为4 m,隧道内设双向行车道,问这辆货车能否安全通过?
(3)在抛物线形拱壁上需要安装两排离地面高度相等的灯,如果灯离地面的高度不超过8.5 m,那么这两排灯的水平距离最小是多少米?
8.如图,是一座古拱桥的截面图,拱桥桥洞的上沿是抛物线形状,当水面的宽度为10m时,桥洞与水面的最大距离是5m.
(1)经过讨论,同学们得出三种建立平面直角坐标系的方案(如图),你选择的方案是 (填方案一,方案二,或方案三),则B点坐标是 ,求出你所选方案中的抛物线的表达式;
(2)因为上游水库泄洪,水面宽度变为6m,求水面上涨的高度.
9.某地欲搭建一桥,桥的底部两端间的距离AB=L,称跨度,桥面最高点到AB的距离CD=h称拱高,当L和h确定时,有两种设计方案可供选择:①抛物线型,②圆弧型. 已知这座桥的跨度L=32米,拱高h=8米.
(1)如果设计成抛物线型,以AB所在直线为x轴, AB的垂直平分线为y轴建立坐标系,求桥拱的函数解析式;
(2)如果设计成圆弧型,求该圆弧所在圆的半径;
(3)在距离桥的一端4米处欲立一桥墩EF支撑,在两种方案中分别求桥墩的高度.
10.某菜农搭建了一个横截面为抛物线的大棚,尺寸如图:
(1)如图建立平面直角坐标系,使抛物线对称轴为y轴,求该抛物线的解析式;
(2)若需要开一个截面为矩形的门(如图所示),已知门的高度为1.60米,那么门的宽度最大是多少米(不考虑材料厚度) (结果保留根号)
11.如图,是一座古拱桥的截面图,拱桥桥洞上沿是抛物线形状,抛物线两端点与水面的距离都是,拱桥的跨度为,桥洞与水面的最大距离是,桥洞两侧壁上各有一盏距离水面的景观灯,把拱桥的截面图放在平面直角坐标系中.
(1)求抛物线对应的函数解析式,并写出自变量的取值范围;
(2)求两盏景观灯之间的水平距离.
12.如图,小河上有一拱桥,拱桥及河道的截面轮廓线由抛物线的一部分ACB和矩形的三边AE、ED、DB组成,已知河底ED是水平的,ED=16m,AE=8m,抛物线的顶点C到ED的距离是11m,以ED所在的直线为x轴,抛物线的对称轴为y轴建立平面直角坐标系.
(1)求抛物线的解析式;
(2)已知从某时刻开始的40h内,水面与河底ED的距离h(单位:m)随时间t(单位:h)的变化满足函数关系h=-(t-19)2+8(0≤t≤40)且当水面到顶点C的距离不大于5m时,需禁止船只通行,请通过计算说明:在这一时段内,需多少小时禁止船只通行?
13.施工队要修建一个横断面为抛物线的公路隧道,其高度为6米,宽度OM为12米.现以O点为原点,OM所在直线为x轴建立直角坐标系(如图1所示).
(1)求出这条抛物线的函数解析式,并写出自变量x的取值范围;
(2)隧道下的公路是双向行车道(正中间是一条宽1米的隔离带),其中的一条行车道能否行驶宽2.5米、高5米的特种车辆?请通过计算说明;
(3)施工队计划在隧道门口搭建一个矩形脚手架CDAB,使A、D点在抛物线上.B、C点在地面OM线上(如图2所示).为了筹备材料,需测算“脚手架”三根钢杆AB、AD、DC的长度之和的最大值是多少,请你帮施工队计算一下.
14.有一个抛物线形的桥洞,桥洞离水面的最大高度BM为3米,跨度OA为6米,以OA所在直线为x轴,O为原点建立直角坐标系(如图所示).
(1)请你直接写出O、A、M三点的坐标;
(2)一艘小船平放着一些长3米,宽2米且厚度均匀的矩形木板,要使该小船能通过此桥洞,问这些木板最高可堆放多少米(设船身底板与水面同一平面)?
15.一隧道内设双行公路,隧道的高MN为6米.下图是隧道的截面示意图,并建立如图所示的直角坐标系,它是由一段抛物线和一个矩形CDEF的三条边围成的,矩形的长DE是8米,宽CD是2米.
(1)求该抛物线的解析式;
(2)为了保证安全,要求行驶的车辆顶部与隧道顶部至少要有0.5米的距离.若行车道总宽度PQ(居中,两边为人行道)为6米,一辆高3.2米的货运卡车(设为长方形)靠近最右边行驶能否安全?请写出判断过程;
(3)施工队计划在隧道门口搭建一个矩形“脚手架”ABHG,使H、G两点在抛物线上,A、B两点在地面DE上,设GH长为n米,“脚手架”三根木杆AG、GH、HB的长度之和为L,当n为何值时L最大,最大值为多少?
16.某工厂大门是一抛物线水泥建筑物(如图),大门地面宽AB=4 m,顶部C离地面高为4.4 m.
(1)以AB所在直线为x轴,抛物线的对称轴为y轴,建立平面直角坐标系,求该抛物线对应的函数表达式;
(2)现有一辆载满货物的汽车欲通过大门,货物顶点距地面2.8 m,装货宽度为2.4 m,请通过计算,判断这辆汽车能否顺利通过大门.
17.某涵洞是抛物线形,它的截面如图所示,现测得水面宽AB=1.6m,涵洞顶点O到水面的距离为2.4m,在图中直角坐标系内,求涵洞所在抛物线的函数表达式.
18.如图:河上有一座抛物线形桥洞,已知桥下的水面离桥拱顶部3m时,水面宽AB=6m,建立如图所示的坐标系.
(1)当水位上升0.5m时,求水面宽度CD为多少米?(结果可保留根号)
(2)有一艘游船它的左右两边缘最宽处有一个长方体形状的遮阳棚,此船正对着桥洞在上述河流中航行,若这船宽(最大宽度)2米,从水面到棚顶高度为1.8米.问这艘船能否从桥下洞通过?
参考答案
1.
解:(1)根据题目条件,A、B、C的坐标分别是(-10,0)、(10,0)、(0,6).
设抛物线的解析式为y=ax2+c,
将B、C的坐标代入y=ax2+c,得
解得a=,c=6.
所以抛物线的表达式是y=x2+6.
(2)可设,于是,
从而支柱EF的长度是10-4.5=5.5米.
(3)设DN是隔离带的宽,NG是三辆车的宽度和,则G点坐标是.
过G点作GH垂直AB交抛物线于H,则.
根据抛物线的特点,可知一条行车道能并排行驶这样的三辆汽车.
2.
(1)设抛物线的解析式为y=ax2+c.
∵点E(0,6),点A(﹣5,3)在此抛物线上,∴,得:,∴此抛物线的解析式为y6;
(2)当x=±3时,y6=4.92>4.5,即这辆货运卡车能顺利通过隧道.
3.
解:把代入得:
,
解得,
∴此时可通过物体的宽度为,
∴能通过;
∵一辆货运卡车高,隧道的截面由抛物线和长方形构成.长方形的长是,宽是,
∴货车上面有,在矩形上面,当时,
,
解得,
∵,
∴能通过.
4.
以点E为原点、EF所在直线为y轴,垂直EF的直线为x轴建立平面直角坐标系,
根据题意知E(0,0)、A(﹣3,﹣3)、B(3,﹣3),
设y=kx2(k<0),
将点(3,﹣3)代入,得:k=﹣,
∴y=﹣x2,
将x=代入,得:y=﹣2,
∴上升了1米.
5.
解:(1)设所求抛物线的解析式为y=ax2.
∵CD=10 m,CD到拱桥顶E的距离仅为1 m,
∴C(-5,-1).
把点C的坐标代入y=ax2,
得a=-,
故抛物线的解析式为y=-x2.
(2)∵AB宽20 m,
∴可设A(-10,b).
把点A的坐标代入抛物线的解析式y=-x2中,
解得b=-4,
∴点A的坐标为(-10,-4).
设AB与y轴交于点F,则F(0,-4),
∴EF=3 m.
∵水位以每小时0.3 m的速度上升,
∴3÷0.3=10(时).
答:从正常水位开始,持续10小时到达警戒线.
6.
试题解析:设抛物线解析式为
把点代入解析式得:
解得:
∴抛物线的解析式为
7.
试题分析:(1)设出抛物线的解析式,根据抛物线顶点坐标,代入解析式;
(2)令x=10,求出y与6作比较;
(3)求出y=8.5时x的值即可得.
试题解析:(1)根据题意,该抛物线的顶点坐标为(6,10),
设抛物线解析式为:y=+10,
将点B(0,4)代入,得:36a+10=4,
解得:a=,
故该抛物线解析式为y=+10;
(2)根据题意,当x=6+4=10时,y=×16+10=>6,
∴这辆货车能安全通过.
(3)当y=8.5时,有:+10=8.5,
解得:=3,=9,
∴﹣=6,
答:两排灯的水平距离最小是6米.
考点:二次函数的应用.
8.
:解:方案1:(1)点B的坐标为(5,0),设抛物线的解析式为:.由题意可以得到抛物线的顶点为(0,5),代入解析式可得:,∴抛物线的解析式为:;
(2)由题意:把代入,解得:=3.2,∴水面上涨的高度为3.2m.
方案2:(1)点B的坐标为(10,0).设抛物线的解析式为:.
由题意可以得到抛物线的顶点为(5,5),代入解析式可得:,∴抛物线的解析式为:;
(2)由题意:把代入解得:=3.2,∴水面上涨的高度为3.2m.
方案3:(1)点B的坐标为(5, ),由题意可以得到抛物线的顶点为(0,0).
设抛物线的解析式为:,把点B的坐标(5, ),代入解析式可得:,
∴抛物线的解析式为:;
(2)由题意:把代入解得:=,∴水面上涨的高度为3.2m.
9.
解析:(1)抛物线的解析式为y=ax2+c,
又∵抛物线经过点C(0,8)和点B(16,0),
∴0=256a+8,a=-.
∴抛物线的解析式为y=-x2+8(-16≤x≤16);
(2)设弧AB所在的圆心为O,C为弧AB的中点,CD⊥AB于D,延长CD经过O点,
设⊙O的半径为R,
在Rt△OBD中,OB2=OD2+DB2
∴R2=(R-8)2+162,解得R=20;
(3)①在抛物线型中设点F(x,y)在抛物线上,x=OE=16-4=12,
EF=y=3.5米;
②在圆弧型中设点F′在弧AB上,作F′E′⊥AB于E′,
OH⊥F′E′于H,则OH=D E′=16-4=12,O F′=R=20,
在Rt△OH F′中,H F′= ,
∵HE′=OD=OC-CD=20-8=12,E′F′=HF′-HE′=16-12=4(米)
∴在离桥的一端4米处,抛物线型桥墩高3.5米; 圆弧型桥墩高4米.
10.
解:(1)由图可设抛物线的解析式为:y=ax2+2,
由图知抛物线与x轴正半轴的交点为(2,0),则:a×22+2=0,
∴a=﹣,
∴抛物线的解析式为y=﹣x2+2;
(2)当y=1.60时,知1.6=﹣x2+2,
解得:x=,
所以门的宽度最大为2×=米.
考点:二次函数的应用.
11.
(1)抛物线的顶点坐标为(5,5),与y轴交点坐标是(0,1),设抛物线的解析式是y=a(x﹣5)2+5,把(0,1)代入y=a(x﹣5)2+5,得:a=﹣,∴y=﹣(x﹣5)2+5(0≤x≤10),即(0≤x≤10);
(2)由已知得两景观灯的纵坐标都是4,∴4=﹣(x﹣5)2+5,∴(x﹣5)2=1,∴x1=,x2=,∴两景观灯间的距离为 ﹣=5米.
12.
二次函数的应用,待定系数法,曲线上点的坐标与方程的关系.
(1)根据抛物线特点设出二次函数解析式,把B坐标代入即可求解.
(2)水面到顶点C的距离不大于5米时,即水面与河底ED的距离h至多为6,把6代入所给二次函数关系式,求得t的值,相减即可得到禁止船只通行的时间.
13.
(1)∵M(12,0),P(6,6).
∴设这条抛物线的函数解析式为y=a(x-6)2+6,
∵把(0,0)代入解得a=-,
∴这条抛物线的函数解析式为y=-(x-6)2+6,
即y=-x2+2x(0≤x≤12);
(2)当x=6-0.5-2.5=3(或x=6+0.5+2.5=9)时,y=4.5<5
∴不能行驶宽2.5米、高5米的特种车辆;
(3)设点A的坐标为(m,-m2+2m),
∴OB=m,AB=DC=-m2+2m
根据抛物线的轴对称可得OB=CM=m,
∴BC=12-2m,即AD=12-2m
∴L=AB+AD+DC=-m2+2m+12=-(m-3)2+15
∴当m=3,即OB=3米时,三根木杆长度之和L的最大值为15米.
14.
解:(1)0(0,0),A(6,0),M(3,3).
(2)设抛物线的关系式为y=a(x-3)2+3,
因为抛物线过点(0,0),
所以0=a(0-3)2+3,
解得a=,
所以,
要使木板堆放最高,依据题意,得B点应是木板宽CD的中点,
把x=2代入,
得,所以这些木板最高可堆放米.
15.
解:(1)由题意得M(0,4),F(4,0)
可设抛物线的解析式为y=ax2+4,
将F(4,0)代入y=ax2+4中,得a=-,
∴抛物线的解析式为y=-x2+4;
(2)当x=3,y=,
+2-=3.253.2,∴能安全通过;
(3)由GH=n,可设H(),
∴GH+GA+BH=n+()×2+2×2=,
∴L=,
∵a<0,抛物线开口向下,
∴当n=-=4时,L有最大值,最大值为14.
16.
解:(1)如图,过AB的中点作AB的垂直平分线,建立平面直角坐标系.点A,B,C的坐标分别为 A(-2,0),B(2,0),C(0,4.4).
设抛物线的表达式为y=a(x-2)(x+2).
将点C(0,4.4)代入得
a(0-2)(0+2)=4.4,解得a=-1.1,
∴y=-1.1(x-2)(x+2)=-1.1x2+4.4.
故此抛物线的表达式为y=-1.1x2+4.4.
(2)∵货物顶点距地面2.8 m,装货宽度为2.4,
∴只要判断点(-1.2,2.8)或点(1.2,2.8)与抛物线的位置关系即可.
将x=1.2代入抛物线,得 y=2.816>2.8,
∴点(-1.2,2.8)和点(1.2,2.8)都在抛物线内.
∴这辆汽车能够通过大门.
17.
解:设此抛物线所对应的函数表达式为:,
∵,涵洞顶点到水面的距离为,
∴点坐标应该是,
把点代入得:,
解得:,
故涵洞所在抛物线的函数表达式.
18.
(1)设抛物线形桥洞的函数解析式为y=ax2+c,
把A(3,0),E(0,3)代入得:
解得:
∴
由题意得:点C与D的纵坐标为0.5,
∴
解得:
∴(米),
则水面的宽度CD为米;
(2)当x=1时,
∵
∴这艘游船能从桥洞下通过.
试卷第2页,共8页
同课章节目录
