2021—2022学年人教版数学九年级下册第二十七章 相似27.2.2相似三角形的性质 课件(共27张PPT)
文档属性
| 名称 | 2021—2022学年人教版数学九年级下册第二十七章 相似27.2.2相似三角形的性质 课件(共27张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 10:05:36 | ||
图片预览


文档简介
(共27张PPT)
27.2.2 相似三角形的性质
人教版九年级下册
情境设疑
新知探究
例题精析
应用新知
中考链接
课堂小结
分层作业
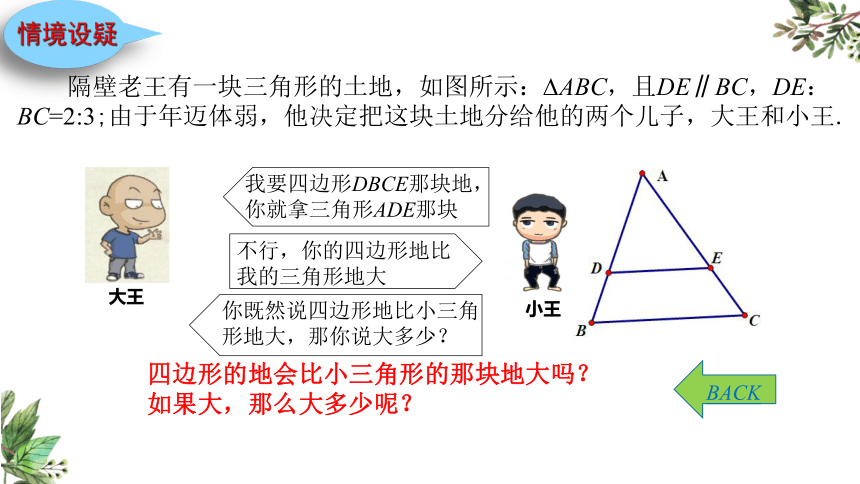
大王
小王
我要四边形DBCE那块地,
你就拿三角形ADE那块
不行,你的四边形地比
我的三角形地大
隔壁老王有一块三角形的土地,如图所示: ABC,且DE∥BC,DE:BC=2:3;由于年迈体弱,他决定把这块土地分给他的两个儿子,大王和小王.
四边形的地会比小三角形的那块地大吗?如果大,那么大多少呢?
你既然说四边形地比小三角形地大,那你说大多少?
情境设疑
BACK
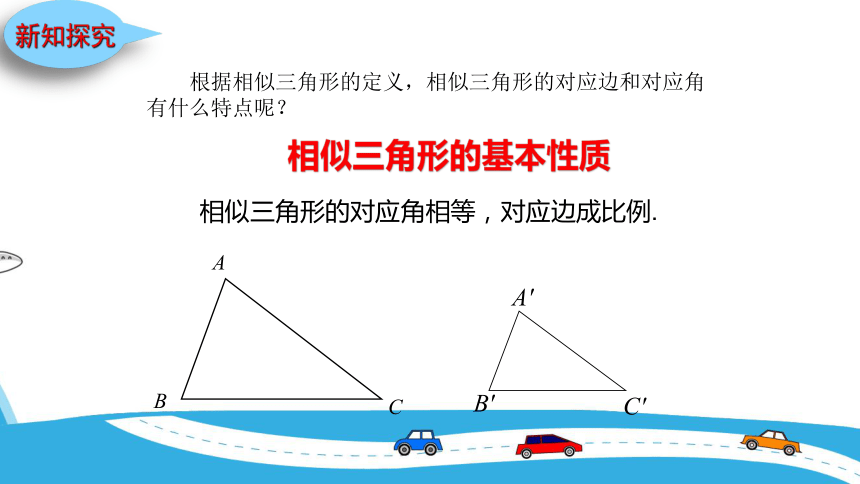
A
B
C
A'
B'
C'
相似三角形的对应角相等,对应边成比例.
相似三角形的基本性质
根据相似三角形的定义,相似三角形的对应边和对应角有什么特点呢?
新知探究
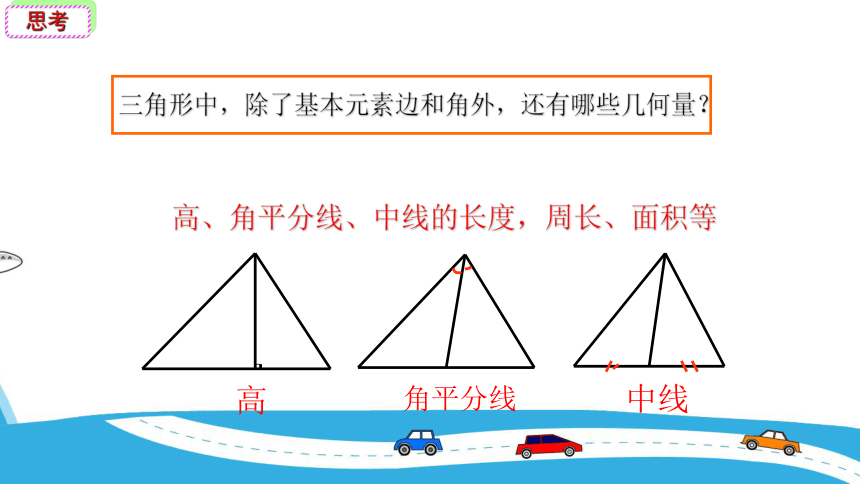
三角形中,除了基本元素边和角外,还有哪些几何量?
高、角平分线、中线的长度,周长、面积等
高
角平分线
中线
思考
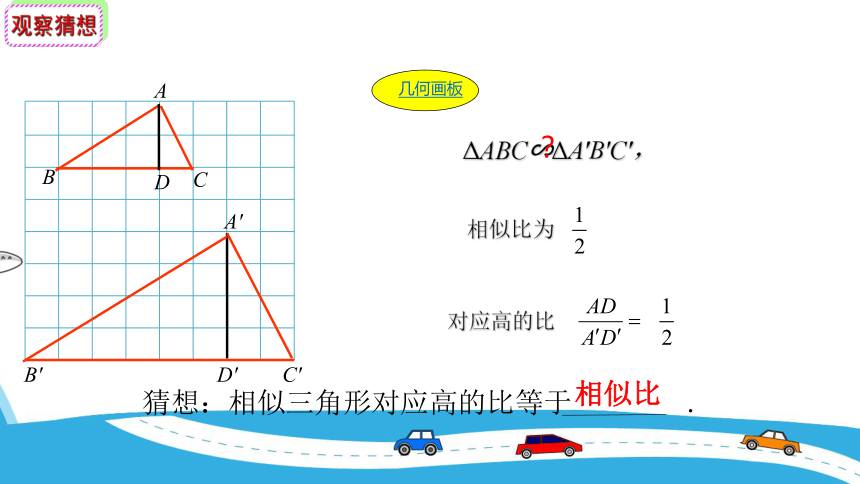
ΔABC∽ΔA'B'C',
对应高的比
相似比为
?
相似比
C
A
B
D
D'
A'
B'
C'
猜想:相似三角形对应高的比等于 .
观察猜想
几何画板
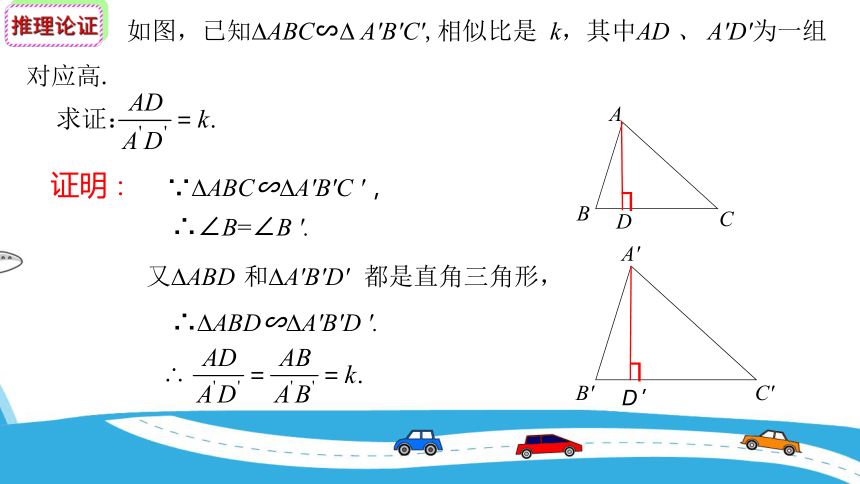
如图,已知 ABC∽ A′B′C′,相似比是 k,其中AD 、 A′D′为一组
对应高.
A
B
C
L
D
证明:
∵ ABC∽ A'B'C ',
∴∠B=∠B '.
又 ABD 和 A'B'D' 都是直角三角形,
∴ ABD∽ A'B'D '.
A'
B'
C'
L
D'
推理论证
相似三角形对应中线的比等于相似比
A'
B'
C'
A
B
C
新知再探
D
D'
D
D'
⌒
⌒
D
⌒
⌒
D'
相似三角形对应角平分线的比等于相似比
相似三角形对应高的比等于相似比
L
L
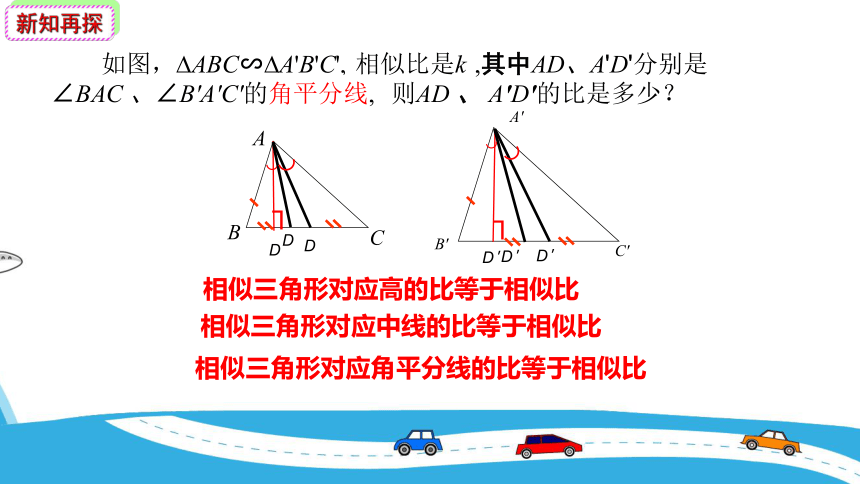
如图, ABC∽ A'B'C', 相似比是k ,其中AD、A'D'分别是
BC、B'C'边上的 ,
则AD 、 A'D'的比是多少?
中线
∠BAC 、∠B'A'C'的角平分线,
相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
相似三角形的性质定理:
进一步推广:
相似三角形对应线段的比等于相似比
问题:两个相似三角形的周长比会等于相似比吗?
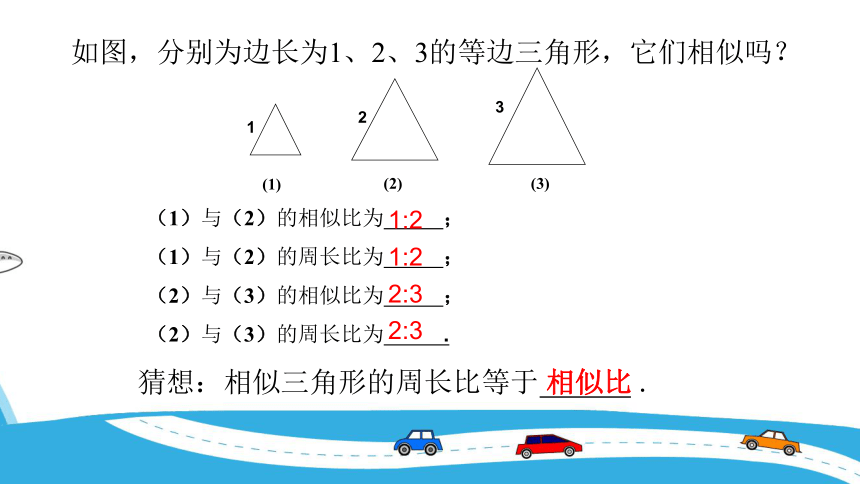
如图,分别为边长为1、2、3的等边三角形,它们相似吗?
(1)与(2)的相似比为 ;
(1)与(2)的周长比为 ;
(2)与(3)的相似比为 ;
(2)与(3)的周长比为 .
(1)
(2)
(3)
3
2
1
1:2
1:2
2:3
2:3
相似比
猜想:相似三角形的周长比等于 .
A
B
C
A'
B'
C'
如果 ABC ∽ A'B'C',相似比为 k,那么
因此
AB=k A'B',BC=kB'C',CA=kC'A',
从而
相似三角形的周长比也等于相似比
巩固新知
1.判断下列说法的对错:
(1)一个三角形的各边扩大为原来的5倍,
这个三角形的角平分线也扩大为原来的5倍;
( )
√
ⅹ
(2)一个三角形的各边缩小为原来的一半,
那这个三角形的周长也缩小为原来的 .
( )
1∶2
(3) ADE的周长︰ ABC的周长=_______.
1∶2
2.如图,DE∥BC,AF⊥ BC交DE于点G,交BC于点F, 且AD= 1,
AB = 2,
(1) ADE与 ABC相似吗?如果相似,求它们的相似比为
小试牛刀
(2)AG:AF=_____
1∶2
相似三角形对应线段的比、周长的比都等于相似比
相似三角形面积的比也等于相似比吗?
新知再探
L
3
3
L
1
1
相似比:3
相似比的平方
猜想:相似三角形的面积比等于
相似三角形面积的比等于相似比的平方
A
B
C
D
L
A'
B'
C'
D'
L
如图,已知 ABC∽ A′B′C′,相似比是 k,其中AD 、 A′D′分别为BC、B'C'边上的高线,则
大王
小王
四边形的地会比小三角形的那块地大吗?如果大,那么大多少呢?
△ADE∽△ABC
四边形的地比三角形的那块地大,
大了 .
隔壁老王有一块三角形的土地,如图所示: ABC,且DE∥BC,DE:BC=2:3;由于年迈体弱,他决定把这块土地分给他的两个儿子,大王和小王.
对应高的比
对应中线的比
对应角平分线的比
周长的比
相
似
三
角
形
相似比.
相似三角形面积的比=
相似三角形的性质
相似比的平方
=
归纳概括
BACK
例1:如图,在 ABC和 DEF中,AB=2DE,AC=2DF,∠A=∠D .若 ABC
的边BC上的高为6,面积为 ,求 DEF的边EF上的高和面积.
思路:
DEF∽ ABC
相似比
对应高的比
平方
面积比
面积
H
L
H'
L
解题策略:相似三角形 相似比 面积比 面积
平方
例题精析
解:在 ABC和 DEF中,
∴ DEF∽ ABC,
DEF与 ABC的相似比为
∵ ABC的边BC上的高为6,面积为 ,
∴ DEF的边EF上的高为
面积为
例1:如图,在 ABC和 DEF中,AB=2DE,AC=2DF,∠A=∠D .若 ABC
的边BC上的高为6,面积为 ,求 DEF的边EF上的高和面积.
H
L
H'
L
BACK
如图 ABC中,D、F在AB上,E、G在AC上,且AD=DF=FB,DE∥FG∥BC,
解:∵DE∥FG∥BC
∴ ADE∽ AFG∽ ABC
应用新知
1.如图, ABC被DE、FG分成面积相等的三部分,即 ,且DE∥FG∥BC,则DE:FG:BC等于
变式训练
A
B
C
D
E
F
G
2.如图,DE∥FG∥BC, DE = 1, BC = 4,FG=2,若 ADE的面积 ,则 AFG与四边形DBCE的面积分别为 .
变式训练
解题策略:相似三角形 相似比 面积比 面积
平方
BACK
(2018江西14题)如图,在△ABC中,AB=8,BC=4,CA=6,CA=6,CD∥AB,BD是∠ABC的平分线,BD交AC于点E,求AE的长.
解:∵BD为∠ABC的平分线,
∴∠ABD=∠CBD,
∵AB∥CD,
∴∠D=∠ABD,
∴∠D=∠CBD,
∴BC=CD,
∵BC=4,
∴CD=4,
∵AB∥CD,
∴△ABE∽△CDE,
∵AC=6=AE+CE,
∴AE=4.
解题策略:角平分线、平行线、等腰三角形“三合一”的模型;“X”型
见平行,找相似
中考链接
BACK
1.相似三角形的性质
相
似
三
角
形
面积的比=
相似比的平方
对应高的比
对应中线的比
对应角平分线的比
周长的比
=相似比.
2.运用相似三角形的性质解题的策略是什么?
相似三角形 相似比 面积比 面积
平方
对应线段的比
3.数学思想:
课堂小结
BACK
转化思想
建模思想
类比思想
2. 如图,在 ABC中,∠BAC=60°,∠ABC=90°,直线l1∥l2∥l3,l1与l2之间的距离是1,l2与l3之间的距离是2,且l1、l2、l3分别过点A、B、C,则边AC的长为 .
1.如图,在 ABCD中,BE=2AE,若 .
分层作业
必做题
3.已知四边形ABCD的面积为1.
①如图,取四边形ABCD各边中点,则图中阴影部分的面积为 .
如图,取四边形ABCD各边的三等分点,则图中阴影部分的面积为 .
②
选做题
取四边形ABCD各边的n(n为大于1的整数)等分点,则图中阴影部分的面积为 .
③
BACK
27.2.2 相似三角形的性质
人教版九年级下册
情境设疑
新知探究
例题精析
应用新知
中考链接
课堂小结
分层作业
大王
小王
我要四边形DBCE那块地,
你就拿三角形ADE那块
不行,你的四边形地比
我的三角形地大
隔壁老王有一块三角形的土地,如图所示: ABC,且DE∥BC,DE:BC=2:3;由于年迈体弱,他决定把这块土地分给他的两个儿子,大王和小王.
四边形的地会比小三角形的那块地大吗?如果大,那么大多少呢?
你既然说四边形地比小三角形地大,那你说大多少?
情境设疑
BACK
A
B
C
A'
B'
C'
相似三角形的对应角相等,对应边成比例.
相似三角形的基本性质
根据相似三角形的定义,相似三角形的对应边和对应角有什么特点呢?
新知探究
三角形中,除了基本元素边和角外,还有哪些几何量?
高、角平分线、中线的长度,周长、面积等
高
角平分线
中线
思考
ΔABC∽ΔA'B'C',
对应高的比
相似比为
?
相似比
C
A
B
D
D'
A'
B'
C'
猜想:相似三角形对应高的比等于 .
观察猜想
几何画板
如图,已知 ABC∽ A′B′C′,相似比是 k,其中AD 、 A′D′为一组
对应高.
A
B
C
L
D
证明:
∵ ABC∽ A'B'C ',
∴∠B=∠B '.
又 ABD 和 A'B'D' 都是直角三角形,
∴ ABD∽ A'B'D '.
A'
B'
C'
L
D'
推理论证
相似三角形对应中线的比等于相似比
A'
B'
C'
A
B
C
新知再探
D
D'
D
D'
⌒
⌒
D
⌒
⌒
D'
相似三角形对应角平分线的比等于相似比
相似三角形对应高的比等于相似比
L
L
如图, ABC∽ A'B'C', 相似比是k ,其中AD、A'D'分别是
BC、B'C'边上的 ,
则AD 、 A'D'的比是多少?
中线
∠BAC 、∠B'A'C'的角平分线,
相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.
相似三角形的性质定理:
进一步推广:
相似三角形对应线段的比等于相似比
问题:两个相似三角形的周长比会等于相似比吗?
如图,分别为边长为1、2、3的等边三角形,它们相似吗?
(1)与(2)的相似比为 ;
(1)与(2)的周长比为 ;
(2)与(3)的相似比为 ;
(2)与(3)的周长比为 .
(1)
(2)
(3)
3
2
1
1:2
1:2
2:3
2:3
相似比
猜想:相似三角形的周长比等于 .
A
B
C
A'
B'
C'
如果 ABC ∽ A'B'C',相似比为 k,那么
因此
AB=k A'B',BC=kB'C',CA=kC'A',
从而
相似三角形的周长比也等于相似比
巩固新知
1.判断下列说法的对错:
(1)一个三角形的各边扩大为原来的5倍,
这个三角形的角平分线也扩大为原来的5倍;
( )
√
ⅹ
(2)一个三角形的各边缩小为原来的一半,
那这个三角形的周长也缩小为原来的 .
( )
1∶2
(3) ADE的周长︰ ABC的周长=_______.
1∶2
2.如图,DE∥BC,AF⊥ BC交DE于点G,交BC于点F, 且AD= 1,
AB = 2,
(1) ADE与 ABC相似吗?如果相似,求它们的相似比为
小试牛刀
(2)AG:AF=_____
1∶2
相似三角形对应线段的比、周长的比都等于相似比
相似三角形面积的比也等于相似比吗?
新知再探
L
3
3
L
1
1
相似比:3
相似比的平方
猜想:相似三角形的面积比等于
相似三角形面积的比等于相似比的平方
A
B
C
D
L
A'
B'
C'
D'
L
如图,已知 ABC∽ A′B′C′,相似比是 k,其中AD 、 A′D′分别为BC、B'C'边上的高线,则
大王
小王
四边形的地会比小三角形的那块地大吗?如果大,那么大多少呢?
△ADE∽△ABC
四边形的地比三角形的那块地大,
大了 .
隔壁老王有一块三角形的土地,如图所示: ABC,且DE∥BC,DE:BC=2:3;由于年迈体弱,他决定把这块土地分给他的两个儿子,大王和小王.
对应高的比
对应中线的比
对应角平分线的比
周长的比
相
似
三
角
形
相似比.
相似三角形面积的比=
相似三角形的性质
相似比的平方
=
归纳概括
BACK
例1:如图,在 ABC和 DEF中,AB=2DE,AC=2DF,∠A=∠D .若 ABC
的边BC上的高为6,面积为 ,求 DEF的边EF上的高和面积.
思路:
DEF∽ ABC
相似比
对应高的比
平方
面积比
面积
H
L
H'
L
解题策略:相似三角形 相似比 面积比 面积
平方
例题精析
解:在 ABC和 DEF中,
∴ DEF∽ ABC,
DEF与 ABC的相似比为
∵ ABC的边BC上的高为6,面积为 ,
∴ DEF的边EF上的高为
面积为
例1:如图,在 ABC和 DEF中,AB=2DE,AC=2DF,∠A=∠D .若 ABC
的边BC上的高为6,面积为 ,求 DEF的边EF上的高和面积.
H
L
H'
L
BACK
如图 ABC中,D、F在AB上,E、G在AC上,且AD=DF=FB,DE∥FG∥BC,
解:∵DE∥FG∥BC
∴ ADE∽ AFG∽ ABC
应用新知
1.如图, ABC被DE、FG分成面积相等的三部分,即 ,且DE∥FG∥BC,则DE:FG:BC等于
变式训练
A
B
C
D
E
F
G
2.如图,DE∥FG∥BC, DE = 1, BC = 4,FG=2,若 ADE的面积 ,则 AFG与四边形DBCE的面积分别为 .
变式训练
解题策略:相似三角形 相似比 面积比 面积
平方
BACK
(2018江西14题)如图,在△ABC中,AB=8,BC=4,CA=6,CA=6,CD∥AB,BD是∠ABC的平分线,BD交AC于点E,求AE的长.
解:∵BD为∠ABC的平分线,
∴∠ABD=∠CBD,
∵AB∥CD,
∴∠D=∠ABD,
∴∠D=∠CBD,
∴BC=CD,
∵BC=4,
∴CD=4,
∵AB∥CD,
∴△ABE∽△CDE,
∵AC=6=AE+CE,
∴AE=4.
解题策略:角平分线、平行线、等腰三角形“三合一”的模型;“X”型
见平行,找相似
中考链接
BACK
1.相似三角形的性质
相
似
三
角
形
面积的比=
相似比的平方
对应高的比
对应中线的比
对应角平分线的比
周长的比
=相似比.
2.运用相似三角形的性质解题的策略是什么?
相似三角形 相似比 面积比 面积
平方
对应线段的比
3.数学思想:
课堂小结
BACK
转化思想
建模思想
类比思想
2. 如图,在 ABC中,∠BAC=60°,∠ABC=90°,直线l1∥l2∥l3,l1与l2之间的距离是1,l2与l3之间的距离是2,且l1、l2、l3分别过点A、B、C,则边AC的长为 .
1.如图,在 ABCD中,BE=2AE,若 .
分层作业
必做题
3.已知四边形ABCD的面积为1.
①如图,取四边形ABCD各边中点,则图中阴影部分的面积为 .
如图,取四边形ABCD各边的三等分点,则图中阴影部分的面积为 .
②
选做题
取四边形ABCD各边的n(n为大于1的整数)等分点,则图中阴影部分的面积为 .
③
BACK
