人教版九年级上册数学第二十二章 二次函数22.3实际问题与一元二次方程--图形运动问题训练(word版含答案)
文档属性
| 名称 | 人教版九年级上册数学第二十二章 二次函数22.3实际问题与一元二次方程--图形运动问题训练(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 10:29:20 | ||
图片预览


文档简介
人教版九年级上册数学22.3实际问题与一元二次方程--图形运动问题训练
1.如图所示,在中,,厘米,.点从点开始沿边向点以厘米/秒的速度移动,点从点开始沿边向点以厘米/秒的速度移动,当点运动到点时停止,点也同时停止.
(1)如果点,分别从点,同时出发,那么几秒后,的面积等于平方厘米?
(2)如果点,分别从点,同时出发,问第几秒时,四边形的面积最小?其最小面积为多少?
2.如图,Rt△ABC中,∠C=90°,AC=6,BC=8,动点P、Q分别从A、C两点同时出发,P点沿边AC向C以每秒3个单位长度的速度运动,Q点沿边BC向B以每秒4个单位长度的速度运动,当P、Q到达终点C、B时,运动停止,设运动时间为t(s).
(1)①当运动停止时,t的值为 ;
②设P、C之间的距离为y,则y与t满足 关系(填“正比例函数”、“一次函数”或“二次函数”);
(2)设△PCQ的面积为S.
①求S的表达式(用含t的式子表示);
②求当t为何值时,S取得最大值,这个最大值是多少?
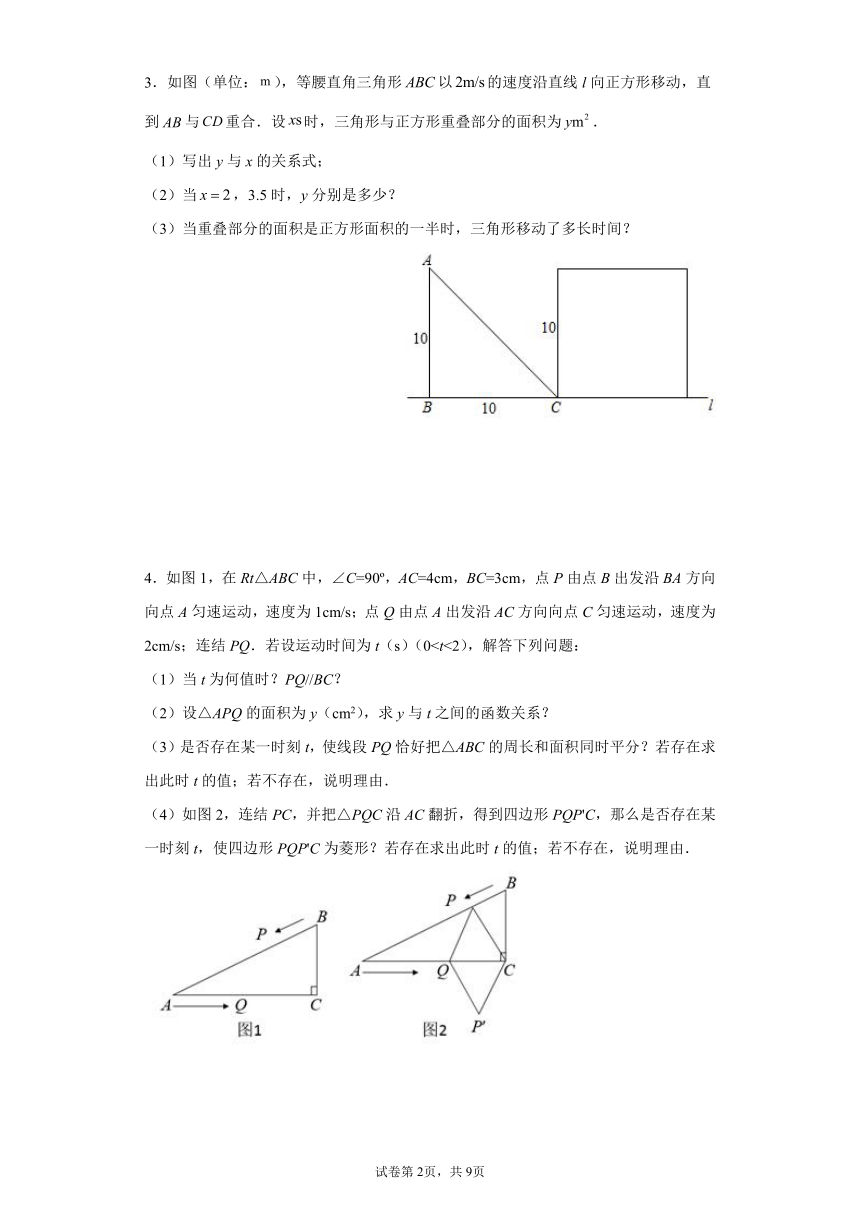
3.如图(单位:),等腰直角三角形以的速度沿直线l向正方形移动,直到与重合.设时,三角形与正方形重叠部分的面积为.
(1)写出y与x的关系式;
(2)当,3.5时,y分别是多少?
(3)当重叠部分的面积是正方形面积的一半时,三角形移动了多长时间?
4.如图1,在Rt△ABC中,∠C=90 ,AC=4cm,BC=3cm,点P由点B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由点A出发沿AC方向向点C匀速运动,速度为2cm/s;连结PQ.若设运动时间为t(s)(0(1)当t为何值时?PQ//BC?
(2)设△APQ的面积为y(cm2),求y与t之间的函数关系?
(3)是否存在某一时刻t,使线段PQ恰好把△ABC的周长和面积同时平分?若存在求出此时t的值;若不存在,说明理由.
(4)如图2,连结PC,并把△PQC沿AC翻折,得到四边形PQP'C,那么是否存在某一时刻t,使四边形PQP'C为菱形?若存在求出此时t的值;若不存在,说明理由.
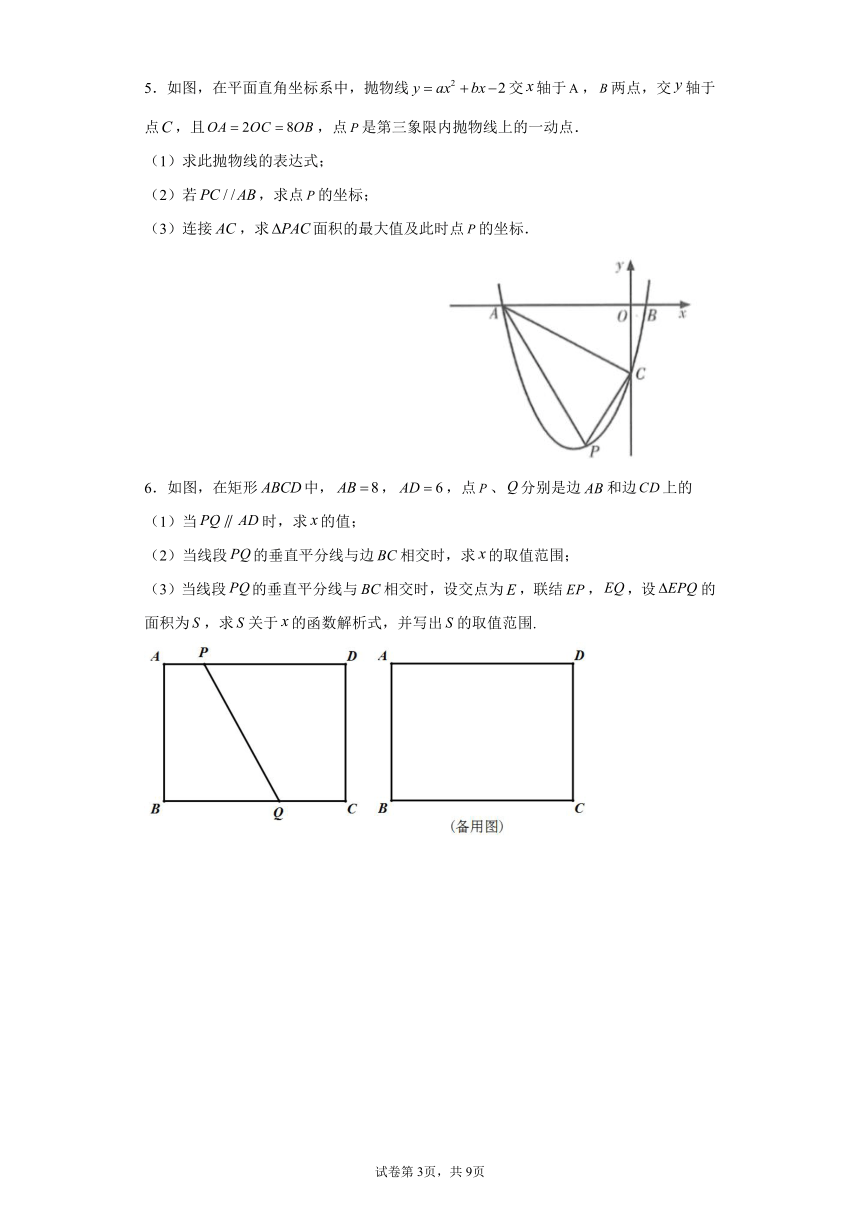
5.如图,在平面直角坐标系中,抛物线交轴于,两点,交轴于点,且,点是第三象限内抛物线上的一动点.
(1)求此抛物线的表达式;
(2)若,求点的坐标;
(3)连接,求面积的最大值及此时点的坐标.
6.如图,在矩形中,,,点、分别是边和边上的
(1)当时,求的值;
(2)当线段的垂直平分线与边相交时,求的取值范围;
(3)当线段的垂直平分线与相交时,设交点为,联结,,设的面积为,求关于的函数解析式,并写出的取值范围.
7.如图,△ABC是边长为3 cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,它们的速度都是1 cm/s,当点P运动到B时,P,Q两点停止运动,设P点运动时间为t(s).
(1)当t为何值时,△PBQ是直角三角形?
(2)设四边形APQC的面积为y(cm2),求y关于t的函数表达式,当t取何值时,四边形APQC的面积最小?并求出最小面积.
8.如图,在直角坐标系xOy中有一梯形ABCO,顶点C在x正半轴上,A、B两点在第一象限;且AB∥CO,AO=BC=2,AB=3,OC=5.点P在x轴上,从点(﹣2,0)出发,以每秒1个单位长度的速度沿x轴向正方向运动;同时,过点P作直线l,使直线l和x轴向正方向夹角为30°.设点P运动了t秒,直线l扫过梯形ABCO的面积为S扫.
(1)求A、B两点的坐标;
(2)当t=2秒时,求S扫的值;
(3)求S扫与t的函数关系式,并求出直线l扫过梯形ABCO面积的时点P的坐标.
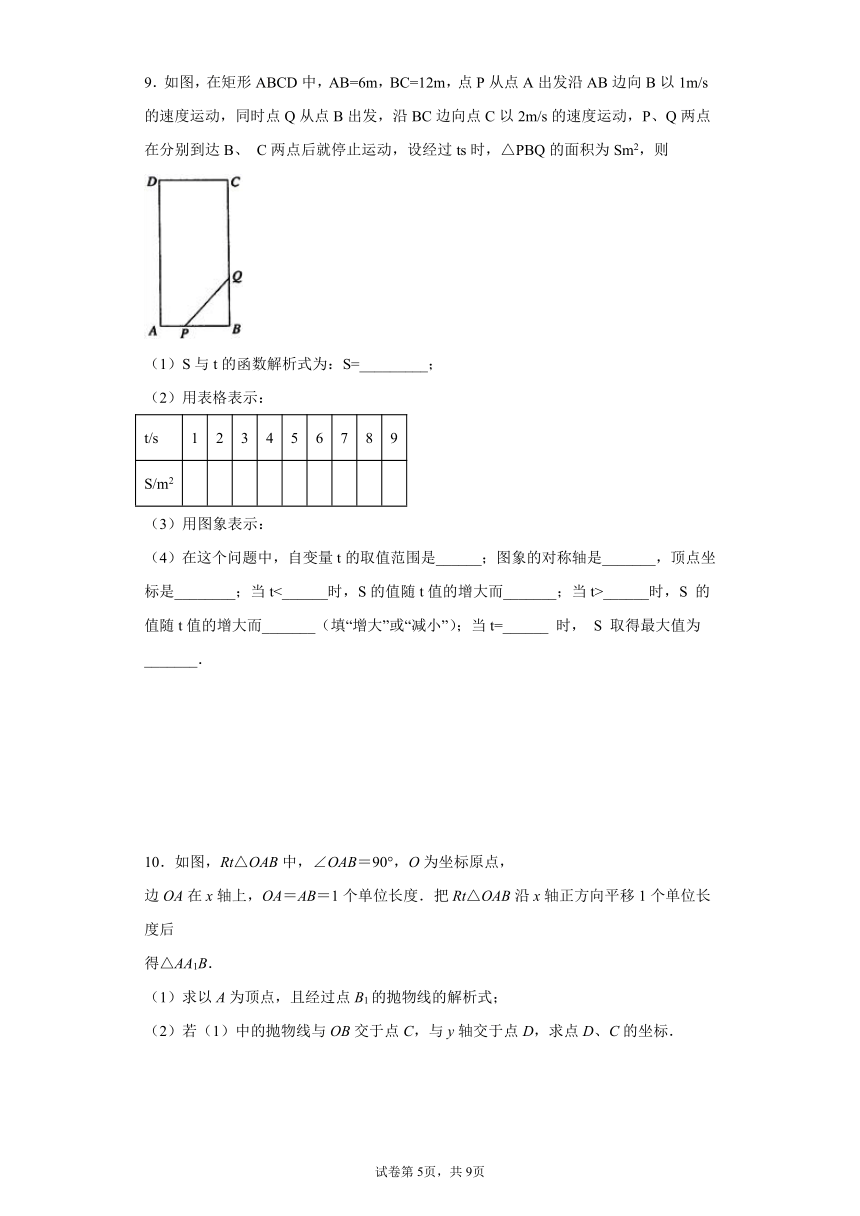
9.如图,在矩形ABCD中,AB=6m,BC=12m,点P从点A出发沿AB边向B以1m/s的速度运动,同时点Q从点B出发,沿BC边向点C以2m/s的速度运动,P、Q两点在分别到达B、C两点后就停止运动,设经过ts时,△PBQ的面积为Sm2,则
(1)S与t的函数解析式为:S=_________;
(2)用表格表示:
t/s 1 2 3 4 5 6 7 8 9
S/m2
(3)用图象表示:
(4)在这个问题中,自变量t的取值范围是______;图象的对称轴是_______,顶点坐标是________;当t<______时,S的值随t值的增大而_______;当t>______时,S的值随t值的增大而_______(填“增大”或“减小”);当t=______时,S取得最大值为_______.
10.如图,Rt△OAB中,∠OAB=90°,O为坐标原点,
边OA在x轴上,OA=AB=1个单位长度.把Rt△OAB沿x轴正方向平移1个单位长度后
得△AA1B.
(1)求以A为顶点,且经过点B1的抛物线的解析式;
(2)若(1)中的抛物线与OB交于点C,与y轴交于点D,求点D、C的坐标.
11.如图,在中,,米,米,动点以米/秒的速度从点出发,沿向点移动.同时,动点以米/秒的速度从点出发,沿向点移动.当其中有一点到达终点时,另一点也随之停止移动.设移动的时间为秒.
(1)①当秒时,求的面积;
②求的面积(米)关于时间(秒)的函数表达式.
(2)在点移动的过程中,当为何值时,为等腰三角形?
12.如图,已知梯形ABCD中,,,,.
(1)求BC的长度.
(2)若点P从点B开始沿BC边向点C以2cm/s的速度运动,点Q从点C开始沿CD边向点D以1cm/s的速度运动,当P,Q分别从B,C同时出发时,求出△PQC的面积S与运动时间t(s)之间的函数关系式,并写出自变量t的取值范围.
(3)写出五边形ABPQD的面积S与运动时间t(s)之间的函数关系式.(不包含点P在B,C两点的情况)
13.如图,在中,,点P从点A开始,沿AB向点B以的速度移动,点Q从B点开始沿BC 以的速度移动,如果P、Q分别从A、B同时出发:
几秒后四边形APQC的面积是31平方厘米;
若用S表示四边形APQC的面积,在经过多长时间S取得最小值?并求出最小值.
14.如图,在平面直角坐标系中,AB∥CD∥x轴,BC∥DE∥y轴,且AB=CD=4cm,OA=5cm,DE=2cm,动点P从点A出发,沿A→B→C路线运动到点C停止;动点Q从点O出发,沿O→E→D路线运动到点D停止.若P,Q两点同时出发,且点P的运动速度为1cm/s,点Q的运动速度为2cm/s.
(1)直接写出B,C,D三个点的坐标;
(2)当P,Q两点出发s时,试求三角形PQC的面积;
(3)设两点运动的时间为ts,用含t的式子表示运动过程中三角形OPQ的面积S(单位:cm2).
15.如图,在△ABC中,AB=AC=4cm,∠BAC=90°.动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为ts,四边形APQC的面积为ycm2 .
(1)当t为何值时,△PBQ是直角三角形
(2)①求y与t的函数关系式,并写出t的取值范围;
②当t为何值时,y取得最小值?最小值为多少?
(3)设PQ的长为xcm,试求y与x的函数关系式.
16.如图所示,已知在直角梯形 OABC 中,AB∥OC,BC⊥x 轴于点 C.A(1,1)、B(3,1).动点 P 从 O 点出发,沿 x 轴正方向以每秒 1 个单位长度的速度移动.过 P 点作 PQ 垂直于直线 OA,垂足为 Q,设 P 点移动的时间为t 秒(0<t<4),△OPQ 与直角梯形 OABC 重叠部分的面积为 S.
(1)求经过 O、A、B 三点的抛物线解析式;
(2)求 S 与 t 的函数关系式;
(3)将△OPQ 绕着点 P 顺时针旋转 90°,是否存 t,使得△OPQ 的顶点 O 或 Q在抛物线上,若存在,直接写出 t 的值;若不存在,请说明理由.
17.如图,对称轴为直线x=-1的抛物线y=a(x-h)-4(a≠0)与x轴相交于A、B两点,与y轴交于点C,其中点A的坐标为(-3,0).
(1)求该抛物线的解析式;
(2)若点P在抛物线上,且S△POC=4S△BOC.求点P的坐标;
(3)设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
18.如图,已知抛物线y=ax2+bx的顶点为C(1,﹣1),P是抛物线上位于第一象限内的一点,直线OP交该抛物线对称轴于点B,直线CP交x轴于点A.
(1)求该抛物线的表达式;
(2)如果点P的横坐标为m,试用m的代数式表示线段BC的长;
(3)如果△ABP的面积等于△ABC的面积,求点P坐标.
参考答案
1.
解:(1)设秒后,的面积等于,则:
,, .
,即,
解得:或(秒不合题意,舍去),
故秒后,的面积等于.
(2)由(1)得,
.
开口向上,时,.
故秒后,四边形的面积最小为.
2.
解:(1)①运动停止时,分别到达终点点和B点,
故答案为
②由题意可得:,,即,∴y与t满足一次函数的关系
故答案为一次函数
(2)①由题意可得:,
△PCQ的面积
故答案为:
②由二次函数的性质可得:,开口向下,对称轴为
∴当时,取得最大值,最大值为
3.
解:(1)因为三角形与正方形重合部分是个等腰直角三角形,且直角边都是2x,
所以y=×2x×2x=2x2;
(2)在y=2x2中,
当x=2时,y=8;
当x=3.5时,y=24.5;
(3)在y=2x2中,
因为当y=50时,2x2=50,
所以x2=25,
解得x=5s(负值舍去).
即当重叠部分的面积是正方形的一半时,三角形移动了5s.
4.
解:(1)连接PQ,
若=时,PQ//BC,即=,
∴t=
(2)过P作PD⊥AC于点D,则有=,
即=,
∴PD=(5-t)
∴y=·2t·(5-t)=-+3t(0(3)若平分周长则有:
AP+AQ=(AB+AC+BC),
即:5-t+2t=6,
∴t=1
当t=1时,y=3.4;而三角形ABC的面积为6,显然不存在.
(4)过P作PD⊥AC于点D,若QD=CD,则PQ=PC,四边形PQP'C就为菱形.
同(2)方法可求AD=(5-t),所以:
(5-t)-2t=4-(5-t);
解之得:t=.
即t=时,四边形PQP'C为菱形.
5.
解:(1)在抛物线中,
令,则,
∴点C的坐标为(0,),
∴OC=2,
∵,
∴,,
∴点A为(,0),点B为(,0),
则把点A、B代入解析式,得
,解得:,
∴;
(2)由题意,∵,点C为(0,),
∴点P的纵坐标为,
令,则,
解得:,,
∴点P的坐标为(,);
(3)设直线AC的解析式为,则
把点A、C代入,得
,解得:,
∴直线AC的解析式为;
过点P作PD∥y轴,交AC于点D,如图:
设点P 为(,),则点D为(,),
∴,
∵OA=4,
∴,
∴,
∴当时,取最大值8;
∴,
∴点P的坐标为(,).
6.
解:(1)当时,则
,,
又,
∴四边形是矩形.
∴.
∵,
,
∴.
(2)如图:
设的垂直平分线交于点,联结、,则,设
∴BP=8-x,BE=6-y
在Rt△PEB和Rt△QEC中,
∴
∴.
∵,
∴.
∴.
(3)由题意可知:
∴
∴
又∵
∴
∴.
∵抛物线开口向上
∴当时,有最小值12;
当或时.有最大值;
∴.
7.
(1)由题意可知,∠B=60°,BP=(3-t)cm,BQ=tcm.若△PBQ是直角三角形,则∠BPQ=30°或∠BQP=30°,于是BQ=BP或BP=BQ,即t= (3-t)或3-t=t.解得t=1或t=2,即当t为1或2时,△PBQ是直角三角形.
(2)如图,过点P作PM⊥BC于点M,
则易知BM=BP= (3-t)cm.
∴PM== (3-t)cm.
∴S四边形APQC=S△ABC-S△PBQ=×3×-t· (3-t)=t2-t+,即y=t2-t+,易知0于是y=(t-)2+
∴当t=时,y取得最小值,为
即当t为时,四边形APQC的面积最小,最小面积为cm2.
8.
(1)过A作AD⊥OC于D,过B作BE⊥OC于E,则ADEB是矩形.
∵ADEB是矩形,∴AD=BE=3.
∵AO=BC,∴△AOD≌△BCE,∴OD=CE=(OC-AB)÷2=1.
∵AO=2,∴AD==,∴A(1,).
∵OE=OD+DE=1+3=4,BE=AD=,∴B(4,).
∵BC=2EC,∴∠EBC=30°,∴∠OCB=60°.
(2)当t=2时,P、O两点重合,如果设直线l与AB的交点为D,那么AD=2,而AD边上的高就是A点的纵坐标,∴S扫==.
(3)分三种情况讨论:①当0≤t<2时,如图1,△AEF∽△AOD,,∴S扫t2;
②当2≤t<3时,如图2,S扫=S△AOD+S□DOPF(t﹣2),∴S扫;
③当3≤t≤7时,如图3,过B作直线EB∥直线l交OC于E.
∵∠BEC=30°,∠OCB=60°,∴∠CBE=90°,∴EC=2BC=4,∴S△CEB=,CP=7-t.
∵MP∥BE,∴,∴S△CPM=,∴S扫=4S△CPM=4,∴S扫t2
综上所述: .
∵t2,∴t2﹣14t+41=0,t1=7﹣2,t2=7+27(舍),∴P的坐标为(5﹣2,0).
9.
试题分析:(1)根据t秒时,P,Q两点的运动路程,分别表示PB,BQ的长度,可得△BPQ的面积S,
(2)把t的值代入解析式可求得对应的S,
(3)通过表格,描点,连线即可求解,
(4)根据二次函数的图象性质可求解.
试题解析:(1)第t秒时,AP=t,则PB=6-t,BQ=2t,所以S=-t2+6t ,
(2)
t/s 1 2 3 4 5 6 7 8 9
S/m2 5 8 9 8 5 0 -7 -16 -27
(3)略
(4)0≤t≤6,t=3,(3,9),3,增大,3,减小,3,9.
10.
(1)由题意可知,A(1,0),A1(2,0),B1(2,1),
设以A为顶点的抛物线的解析式为y=a(x-1)2;
∵此抛物线过点B1(2,1),
∴1=a(2-1)2,
∴a=1,
∴抛物线的解析式为y=(x-1)2;
(2)∵当x=0时,y=(0-1)2=1,
∴D点坐标为(0,1),
由题意得OB在第一象限的角平分线上,
故可设C(m,m),
代入y=(x-1)2;得m=(m-1)2;
解得m1=<1,m2=>1(舍去).
故C点坐标为(,).
考点:二次函数综合题.
11.
在中,米,米,米.
由题意,得米,米,则米.
(1)①如图(a),过点作于点.
当秒时,(米),米,
易知为的中位线,
米,
(米).
②如图(b),过点作于点,
则,,米.
().
(2)当时,由米,米,
得,解得;
当时,如图(c),过点作,
则米,米,可证,
故,即,解得;
当时,如图(d),过点作,
则米,米,可证,
故,即,解得.
故当的值为或或时,为等腰三角形.
12.
解:(1)在Rt△BCD中,,,
∴,
∴(cm);
(2)当P,Q分别从B,C同时出发ts时,,;∴.
如图,过点Q作于点E,则.
∴;
(3)由(2)知,.
∵,,梯形ABCD是等腰梯形.
∴.
又∵,,
∴.
∴.
∴,
∴.
13.
设经过x秒钟,可使得四边形APQC的面积是31平方厘米,
根据题意得:,
即,
整理得,
解得:,.
答:经过1或5秒钟,可使得四边形APQC的面积是31平方厘米;
依题意得,,
即,
当,即时,.
答:经过3秒时,S取得最小值27平方厘米.
14.
解:(1)B(4,5),C(4,2),D(8,2);
(2)当t=s时,点P运动的路程为,
点Q运动的路程为×2=11,
所以,P(4,),Q(7,2),
∴CP=,CQ=3,
∴S△CPQ=CP CQ=××3=;
(3)由题意得,
①当0≤t<4时,(如图1)OA=5,OQ=2t,
S△OPQ=OQ OA=×2t×5=5t;
②当4≤t<5时,(如图2)OE=8,EM=9﹣t,PM=4,MQ=17﹣3t,EQ=2t﹣8,
S△OPQ=S梯形OPMB﹣S△PMQ﹣S△OEQ,
=(4+8)×(9﹣t)﹣×4(17﹣3t)﹣×8(2t﹣8),
=52﹣8t;
③当5≤t≤7时,(如图3)PF=14﹣2t,FQ=7﹣t,QG=2,OG=18﹣2t,FG=9﹣t,
S△OPQ=S梯形OPFG﹣S△PFQ﹣S△OGQ,
=×(14﹣2t+18﹣2t)×(9﹣t)﹣×(14﹣2t)(7﹣t)﹣(18﹣2t)×2,
=t2﹣18t+77,
综上所述,S=.
考点:坐标与图形性质;平行线的性质;三角形的面积.
15.
【详解】
试题分析:(1)分∠PQB=90°和∠QPB=90°两种情况讨论即可;
(2)根据三角形的面积公式列式y=S△ABC-S△BPQ即得函数关系式,根据二次函数最值原理即可得出y取得最小值时t的值和y的最小值;
(3)把t2-4 t=代入y=8-化简即可.
试题解析:(1)当t=或时,△PBQ是直角三角形,理由如下:
∵BQ=AP=t, BP=4-t,
∴①当∠PQB=90°时,由得: t =4-t,解得:t=;
②当∠QPB=90°时,由得:,解得:t=.
∴当t=或时,△PBQ是直角三角形.
(2)①过P作PH⊥BC,在Rt△PHB中,BP=4-t,PH=,
∴S△BPQ=,
∴y=S△ABC-S△BPQ=8-.
由题意可知:0≤t≤4.
②y=8-=,
∴当t=2时,y取得最小值,最小值是.
(3)在Rt△PQH中,PH=(4-t),HQ=(4-t)-t,
由PQ2= PH2+HQ2,则x2=〔(4-t)〕2+〔(4-t)-t〕2
化简得:x2=(2+)t 2-4(2+)t+16,∴ t2-4 t=.
将t2-4t=代入y=8-,得y=8+·.
16.
解:(1)法一:由图象可知:抛物线经过原点,
设抛物线解析式为. 把,代入上式得:
解得
∴所求抛物线解析式为
法二:∵,, ∴抛物线的对称轴是直线.
设抛物线解析式为()
把,代入得解得
∴所求抛物线解析式为
(2)分三种情况:
①当,重叠部分的面积是,过点作轴于点,
∵,在中,,,在中,,
,
∴,
∴
②当,设交于点,作轴于点,
,则四边形是等腰梯形,重叠部分的面积是.
∴,
∴
③当,设与交于点,交于点,重叠部分的面积是.
因为和都是等腰直角三角形,所以重叠部分的面积是
.
∵,,
∴,
∴,
∴
(3)存在t1=1,t2=2.
将△OPQ绕着点P顺时针旋转90°,此时Q(t+,),O(t,t)
①当点Q在抛物线上时,= ×(t+)2+×(t+),解得t=2;
②当点O在抛物线上时,t=-t2+t,解得t=1.
17.
(1)由题意对称轴为直线,
设抛物线解析式为,把点代入得,
.
∴所求抛物线的解析式是.
(2)如图1.
,当时,.所以点,.
令,解得,或.点,.
设点.
此时.
.
由得.
解得或.
所以或.
所以点的坐标为,或.
(3)如图2.
设直线的解析式为:.
把,代入得,解得.
所以直线AC的解析式为.
设点,点.
所以.
所以当时,有最大值.
18.
∵抛物线y=ax2+bx的顶点为C(1,﹣1),
∴,解得:,
∴抛物线的表达式为:y=x2﹣2x;
(2)∵点P的横坐标为m,
∴点P的纵坐标为:m2﹣2m,
令BC与x轴交点为M,过点P作PN⊥x轴,垂足为点N.
∵P是抛物线上位于第一象限内的一点,
∴PN=m2﹣2m,ON=m,OM=1,由=,得:=,
∴BM=m﹣2.
∵点C的坐标为(1,﹣1),
∴BC=m﹣2+1=m﹣1;
(3)令P(t,t2﹣2t).
∵△ABP的面积等于△ABC的面积,
∴AC=AP,过点P作PQ⊥BC交BC于点Q,
∴CM=MQ=1,可得:t2﹣2t=1,解得:t=1+(t=1﹣舍去),
∴P的坐标为(1+,1).
试卷第8页,共9页
试卷第9页,共9页
1.如图所示,在中,,厘米,.点从点开始沿边向点以厘米/秒的速度移动,点从点开始沿边向点以厘米/秒的速度移动,当点运动到点时停止,点也同时停止.
(1)如果点,分别从点,同时出发,那么几秒后,的面积等于平方厘米?
(2)如果点,分别从点,同时出发,问第几秒时,四边形的面积最小?其最小面积为多少?
2.如图,Rt△ABC中,∠C=90°,AC=6,BC=8,动点P、Q分别从A、C两点同时出发,P点沿边AC向C以每秒3个单位长度的速度运动,Q点沿边BC向B以每秒4个单位长度的速度运动,当P、Q到达终点C、B时,运动停止,设运动时间为t(s).
(1)①当运动停止时,t的值为 ;
②设P、C之间的距离为y,则y与t满足 关系(填“正比例函数”、“一次函数”或“二次函数”);
(2)设△PCQ的面积为S.
①求S的表达式(用含t的式子表示);
②求当t为何值时,S取得最大值,这个最大值是多少?
3.如图(单位:),等腰直角三角形以的速度沿直线l向正方形移动,直到与重合.设时,三角形与正方形重叠部分的面积为.
(1)写出y与x的关系式;
(2)当,3.5时,y分别是多少?
(3)当重叠部分的面积是正方形面积的一半时,三角形移动了多长时间?
4.如图1,在Rt△ABC中,∠C=90 ,AC=4cm,BC=3cm,点P由点B出发沿BA方向向点A匀速运动,速度为1cm/s;点Q由点A出发沿AC方向向点C匀速运动,速度为2cm/s;连结PQ.若设运动时间为t(s)(0
(2)设△APQ的面积为y(cm2),求y与t之间的函数关系?
(3)是否存在某一时刻t,使线段PQ恰好把△ABC的周长和面积同时平分?若存在求出此时t的值;若不存在,说明理由.
(4)如图2,连结PC,并把△PQC沿AC翻折,得到四边形PQP'C,那么是否存在某一时刻t,使四边形PQP'C为菱形?若存在求出此时t的值;若不存在,说明理由.
5.如图,在平面直角坐标系中,抛物线交轴于,两点,交轴于点,且,点是第三象限内抛物线上的一动点.
(1)求此抛物线的表达式;
(2)若,求点的坐标;
(3)连接,求面积的最大值及此时点的坐标.
6.如图,在矩形中,,,点、分别是边和边上的
(1)当时,求的值;
(2)当线段的垂直平分线与边相交时,求的取值范围;
(3)当线段的垂直平分线与相交时,设交点为,联结,,设的面积为,求关于的函数解析式,并写出的取值范围.
7.如图,△ABC是边长为3 cm的等边三角形,动点P,Q同时从A,B两点出发,分别沿AB,BC方向匀速移动,它们的速度都是1 cm/s,当点P运动到B时,P,Q两点停止运动,设P点运动时间为t(s).
(1)当t为何值时,△PBQ是直角三角形?
(2)设四边形APQC的面积为y(cm2),求y关于t的函数表达式,当t取何值时,四边形APQC的面积最小?并求出最小面积.
8.如图,在直角坐标系xOy中有一梯形ABCO,顶点C在x正半轴上,A、B两点在第一象限;且AB∥CO,AO=BC=2,AB=3,OC=5.点P在x轴上,从点(﹣2,0)出发,以每秒1个单位长度的速度沿x轴向正方向运动;同时,过点P作直线l,使直线l和x轴向正方向夹角为30°.设点P运动了t秒,直线l扫过梯形ABCO的面积为S扫.
(1)求A、B两点的坐标;
(2)当t=2秒时,求S扫的值;
(3)求S扫与t的函数关系式,并求出直线l扫过梯形ABCO面积的时点P的坐标.
9.如图,在矩形ABCD中,AB=6m,BC=12m,点P从点A出发沿AB边向B以1m/s的速度运动,同时点Q从点B出发,沿BC边向点C以2m/s的速度运动,P、Q两点在分别到达B、C两点后就停止运动,设经过ts时,△PBQ的面积为Sm2,则
(1)S与t的函数解析式为:S=_________;
(2)用表格表示:
t/s 1 2 3 4 5 6 7 8 9
S/m2
(3)用图象表示:
(4)在这个问题中,自变量t的取值范围是______;图象的对称轴是_______,顶点坐标是________;当t<______时,S的值随t值的增大而_______;当t>______时,S的值随t值的增大而_______(填“增大”或“减小”);当t=______时,S取得最大值为_______.
10.如图,Rt△OAB中,∠OAB=90°,O为坐标原点,
边OA在x轴上,OA=AB=1个单位长度.把Rt△OAB沿x轴正方向平移1个单位长度后
得△AA1B.
(1)求以A为顶点,且经过点B1的抛物线的解析式;
(2)若(1)中的抛物线与OB交于点C,与y轴交于点D,求点D、C的坐标.
11.如图,在中,,米,米,动点以米/秒的速度从点出发,沿向点移动.同时,动点以米/秒的速度从点出发,沿向点移动.当其中有一点到达终点时,另一点也随之停止移动.设移动的时间为秒.
(1)①当秒时,求的面积;
②求的面积(米)关于时间(秒)的函数表达式.
(2)在点移动的过程中,当为何值时,为等腰三角形?
12.如图,已知梯形ABCD中,,,,.
(1)求BC的长度.
(2)若点P从点B开始沿BC边向点C以2cm/s的速度运动,点Q从点C开始沿CD边向点D以1cm/s的速度运动,当P,Q分别从B,C同时出发时,求出△PQC的面积S与运动时间t(s)之间的函数关系式,并写出自变量t的取值范围.
(3)写出五边形ABPQD的面积S与运动时间t(s)之间的函数关系式.(不包含点P在B,C两点的情况)
13.如图,在中,,点P从点A开始,沿AB向点B以的速度移动,点Q从B点开始沿BC 以的速度移动,如果P、Q分别从A、B同时出发:
几秒后四边形APQC的面积是31平方厘米;
若用S表示四边形APQC的面积,在经过多长时间S取得最小值?并求出最小值.
14.如图,在平面直角坐标系中,AB∥CD∥x轴,BC∥DE∥y轴,且AB=CD=4cm,OA=5cm,DE=2cm,动点P从点A出发,沿A→B→C路线运动到点C停止;动点Q从点O出发,沿O→E→D路线运动到点D停止.若P,Q两点同时出发,且点P的运动速度为1cm/s,点Q的运动速度为2cm/s.
(1)直接写出B,C,D三个点的坐标;
(2)当P,Q两点出发s时,试求三角形PQC的面积;
(3)设两点运动的时间为ts,用含t的式子表示运动过程中三角形OPQ的面积S(单位:cm2).
15.如图,在△ABC中,AB=AC=4cm,∠BAC=90°.动点P、Q同时从A、B两点出发,分别沿AB、BC方向匀速移动,它们的速度都是1cm/s,当点P到达点B时,P、Q两点停止运动.设点P的运动时间为ts,四边形APQC的面积为ycm2 .
(1)当t为何值时,△PBQ是直角三角形
(2)①求y与t的函数关系式,并写出t的取值范围;
②当t为何值时,y取得最小值?最小值为多少?
(3)设PQ的长为xcm,试求y与x的函数关系式.
16.如图所示,已知在直角梯形 OABC 中,AB∥OC,BC⊥x 轴于点 C.A(1,1)、B(3,1).动点 P 从 O 点出发,沿 x 轴正方向以每秒 1 个单位长度的速度移动.过 P 点作 PQ 垂直于直线 OA,垂足为 Q,设 P 点移动的时间为t 秒(0<t<4),△OPQ 与直角梯形 OABC 重叠部分的面积为 S.
(1)求经过 O、A、B 三点的抛物线解析式;
(2)求 S 与 t 的函数关系式;
(3)将△OPQ 绕着点 P 顺时针旋转 90°,是否存 t,使得△OPQ 的顶点 O 或 Q在抛物线上,若存在,直接写出 t 的值;若不存在,请说明理由.
17.如图,对称轴为直线x=-1的抛物线y=a(x-h)-4(a≠0)与x轴相交于A、B两点,与y轴交于点C,其中点A的坐标为(-3,0).
(1)求该抛物线的解析式;
(2)若点P在抛物线上,且S△POC=4S△BOC.求点P的坐标;
(3)设点Q是线段AC上的动点,作QD⊥x轴交抛物线于点D,求线段QD长度的最大值.
18.如图,已知抛物线y=ax2+bx的顶点为C(1,﹣1),P是抛物线上位于第一象限内的一点,直线OP交该抛物线对称轴于点B,直线CP交x轴于点A.
(1)求该抛物线的表达式;
(2)如果点P的横坐标为m,试用m的代数式表示线段BC的长;
(3)如果△ABP的面积等于△ABC的面积,求点P坐标.
参考答案
1.
解:(1)设秒后,的面积等于,则:
,, .
,即,
解得:或(秒不合题意,舍去),
故秒后,的面积等于.
(2)由(1)得,
.
开口向上,时,.
故秒后,四边形的面积最小为.
2.
解:(1)①运动停止时,分别到达终点点和B点,
故答案为
②由题意可得:,,即,∴y与t满足一次函数的关系
故答案为一次函数
(2)①由题意可得:,
△PCQ的面积
故答案为:
②由二次函数的性质可得:,开口向下,对称轴为
∴当时,取得最大值,最大值为
3.
解:(1)因为三角形与正方形重合部分是个等腰直角三角形,且直角边都是2x,
所以y=×2x×2x=2x2;
(2)在y=2x2中,
当x=2时,y=8;
当x=3.5时,y=24.5;
(3)在y=2x2中,
因为当y=50时,2x2=50,
所以x2=25,
解得x=5s(负值舍去).
即当重叠部分的面积是正方形的一半时,三角形移动了5s.
4.
解:(1)连接PQ,
若=时,PQ//BC,即=,
∴t=
(2)过P作PD⊥AC于点D,则有=,
即=,
∴PD=(5-t)
∴y=·2t·(5-t)=-+3t(0
AP+AQ=(AB+AC+BC),
即:5-t+2t=6,
∴t=1
当t=1时,y=3.4;而三角形ABC的面积为6,显然不存在.
(4)过P作PD⊥AC于点D,若QD=CD,则PQ=PC,四边形PQP'C就为菱形.
同(2)方法可求AD=(5-t),所以:
(5-t)-2t=4-(5-t);
解之得:t=.
即t=时,四边形PQP'C为菱形.
5.
解:(1)在抛物线中,
令,则,
∴点C的坐标为(0,),
∴OC=2,
∵,
∴,,
∴点A为(,0),点B为(,0),
则把点A、B代入解析式,得
,解得:,
∴;
(2)由题意,∵,点C为(0,),
∴点P的纵坐标为,
令,则,
解得:,,
∴点P的坐标为(,);
(3)设直线AC的解析式为,则
把点A、C代入,得
,解得:,
∴直线AC的解析式为;
过点P作PD∥y轴,交AC于点D,如图:
设点P 为(,),则点D为(,),
∴,
∵OA=4,
∴,
∴,
∴当时,取最大值8;
∴,
∴点P的坐标为(,).
6.
解:(1)当时,则
,,
又,
∴四边形是矩形.
∴.
∵,
,
∴.
(2)如图:
设的垂直平分线交于点,联结、,则,设
∴BP=8-x,BE=6-y
在Rt△PEB和Rt△QEC中,
∴
∴.
∵,
∴.
∴.
(3)由题意可知:
∴
∴
又∵
∴
∴.
∵抛物线开口向上
∴当时,有最小值12;
当或时.有最大值;
∴.
7.
(1)由题意可知,∠B=60°,BP=(3-t)cm,BQ=tcm.若△PBQ是直角三角形,则∠BPQ=30°或∠BQP=30°,于是BQ=BP或BP=BQ,即t= (3-t)或3-t=t.解得t=1或t=2,即当t为1或2时,△PBQ是直角三角形.
(2)如图,过点P作PM⊥BC于点M,
则易知BM=BP= (3-t)cm.
∴PM== (3-t)cm.
∴S四边形APQC=S△ABC-S△PBQ=×3×-t· (3-t)=t2-t+,即y=t2-t+,易知0
∴当t=时,y取得最小值,为
即当t为时,四边形APQC的面积最小,最小面积为cm2.
8.
(1)过A作AD⊥OC于D,过B作BE⊥OC于E,则ADEB是矩形.
∵ADEB是矩形,∴AD=BE=3.
∵AO=BC,∴△AOD≌△BCE,∴OD=CE=(OC-AB)÷2=1.
∵AO=2,∴AD==,∴A(1,).
∵OE=OD+DE=1+3=4,BE=AD=,∴B(4,).
∵BC=2EC,∴∠EBC=30°,∴∠OCB=60°.
(2)当t=2时,P、O两点重合,如果设直线l与AB的交点为D,那么AD=2,而AD边上的高就是A点的纵坐标,∴S扫==.
(3)分三种情况讨论:①当0≤t<2时,如图1,△AEF∽△AOD,,∴S扫t2;
②当2≤t<3时,如图2,S扫=S△AOD+S□DOPF(t﹣2),∴S扫;
③当3≤t≤7时,如图3,过B作直线EB∥直线l交OC于E.
∵∠BEC=30°,∠OCB=60°,∴∠CBE=90°,∴EC=2BC=4,∴S△CEB=,CP=7-t.
∵MP∥BE,∴,∴S△CPM=,∴S扫=4S△CPM=4,∴S扫t2
综上所述: .
∵t2,∴t2﹣14t+41=0,t1=7﹣2,t2=7+27(舍),∴P的坐标为(5﹣2,0).
9.
试题分析:(1)根据t秒时,P,Q两点的运动路程,分别表示PB,BQ的长度,可得△BPQ的面积S,
(2)把t的值代入解析式可求得对应的S,
(3)通过表格,描点,连线即可求解,
(4)根据二次函数的图象性质可求解.
试题解析:(1)第t秒时,AP=t,则PB=6-t,BQ=2t,所以S=-t2+6t ,
(2)
t/s 1 2 3 4 5 6 7 8 9
S/m2 5 8 9 8 5 0 -7 -16 -27
(3)略
(4)0≤t≤6,t=3,(3,9),3,增大,3,减小,3,9.
10.
(1)由题意可知,A(1,0),A1(2,0),B1(2,1),
设以A为顶点的抛物线的解析式为y=a(x-1)2;
∵此抛物线过点B1(2,1),
∴1=a(2-1)2,
∴a=1,
∴抛物线的解析式为y=(x-1)2;
(2)∵当x=0时,y=(0-1)2=1,
∴D点坐标为(0,1),
由题意得OB在第一象限的角平分线上,
故可设C(m,m),
代入y=(x-1)2;得m=(m-1)2;
解得m1=<1,m2=>1(舍去).
故C点坐标为(,).
考点:二次函数综合题.
11.
在中,米,米,米.
由题意,得米,米,则米.
(1)①如图(a),过点作于点.
当秒时,(米),米,
易知为的中位线,
米,
(米).
②如图(b),过点作于点,
则,,米.
().
(2)当时,由米,米,
得,解得;
当时,如图(c),过点作,
则米,米,可证,
故,即,解得;
当时,如图(d),过点作,
则米,米,可证,
故,即,解得.
故当的值为或或时,为等腰三角形.
12.
解:(1)在Rt△BCD中,,,
∴,
∴(cm);
(2)当P,Q分别从B,C同时出发ts时,,;∴.
如图,过点Q作于点E,则.
∴;
(3)由(2)知,.
∵,,梯形ABCD是等腰梯形.
∴.
又∵,,
∴.
∴.
∴,
∴.
13.
设经过x秒钟,可使得四边形APQC的面积是31平方厘米,
根据题意得:,
即,
整理得,
解得:,.
答:经过1或5秒钟,可使得四边形APQC的面积是31平方厘米;
依题意得,,
即,
当,即时,.
答:经过3秒时,S取得最小值27平方厘米.
14.
解:(1)B(4,5),C(4,2),D(8,2);
(2)当t=s时,点P运动的路程为,
点Q运动的路程为×2=11,
所以,P(4,),Q(7,2),
∴CP=,CQ=3,
∴S△CPQ=CP CQ=××3=;
(3)由题意得,
①当0≤t<4时,(如图1)OA=5,OQ=2t,
S△OPQ=OQ OA=×2t×5=5t;
②当4≤t<5时,(如图2)OE=8,EM=9﹣t,PM=4,MQ=17﹣3t,EQ=2t﹣8,
S△OPQ=S梯形OPMB﹣S△PMQ﹣S△OEQ,
=(4+8)×(9﹣t)﹣×4(17﹣3t)﹣×8(2t﹣8),
=52﹣8t;
③当5≤t≤7时,(如图3)PF=14﹣2t,FQ=7﹣t,QG=2,OG=18﹣2t,FG=9﹣t,
S△OPQ=S梯形OPFG﹣S△PFQ﹣S△OGQ,
=×(14﹣2t+18﹣2t)×(9﹣t)﹣×(14﹣2t)(7﹣t)﹣(18﹣2t)×2,
=t2﹣18t+77,
综上所述,S=.
考点:坐标与图形性质;平行线的性质;三角形的面积.
15.
【详解】
试题分析:(1)分∠PQB=90°和∠QPB=90°两种情况讨论即可;
(2)根据三角形的面积公式列式y=S△ABC-S△BPQ即得函数关系式,根据二次函数最值原理即可得出y取得最小值时t的值和y的最小值;
(3)把t2-4 t=代入y=8-化简即可.
试题解析:(1)当t=或时,△PBQ是直角三角形,理由如下:
∵BQ=AP=t, BP=4-t,
∴①当∠PQB=90°时,由得: t =4-t,解得:t=;
②当∠QPB=90°时,由得:,解得:t=.
∴当t=或时,△PBQ是直角三角形.
(2)①过P作PH⊥BC,在Rt△PHB中,BP=4-t,PH=,
∴S△BPQ=,
∴y=S△ABC-S△BPQ=8-.
由题意可知:0≤t≤4.
②y=8-=,
∴当t=2时,y取得最小值,最小值是.
(3)在Rt△PQH中,PH=(4-t),HQ=(4-t)-t,
由PQ2= PH2+HQ2,则x2=〔(4-t)〕2+〔(4-t)-t〕2
化简得:x2=(2+)t 2-4(2+)t+16,∴ t2-4 t=.
将t2-4t=代入y=8-,得y=8+·.
16.
解:(1)法一:由图象可知:抛物线经过原点,
设抛物线解析式为. 把,代入上式得:
解得
∴所求抛物线解析式为
法二:∵,, ∴抛物线的对称轴是直线.
设抛物线解析式为()
把,代入得解得
∴所求抛物线解析式为
(2)分三种情况:
①当,重叠部分的面积是,过点作轴于点,
∵,在中,,,在中,,
,
∴,
∴
②当,设交于点,作轴于点,
,则四边形是等腰梯形,重叠部分的面积是.
∴,
∴
③当,设与交于点,交于点,重叠部分的面积是.
因为和都是等腰直角三角形,所以重叠部分的面积是
.
∵,,
∴,
∴,
∴
(3)存在t1=1,t2=2.
将△OPQ绕着点P顺时针旋转90°,此时Q(t+,),O(t,t)
①当点Q在抛物线上时,= ×(t+)2+×(t+),解得t=2;
②当点O在抛物线上时,t=-t2+t,解得t=1.
17.
(1)由题意对称轴为直线,
设抛物线解析式为,把点代入得,
.
∴所求抛物线的解析式是.
(2)如图1.
,当时,.所以点,.
令,解得,或.点,.
设点.
此时.
.
由得.
解得或.
所以或.
所以点的坐标为,或.
(3)如图2.
设直线的解析式为:.
把,代入得,解得.
所以直线AC的解析式为.
设点,点.
所以.
所以当时,有最大值.
18.
∵抛物线y=ax2+bx的顶点为C(1,﹣1),
∴,解得:,
∴抛物线的表达式为:y=x2﹣2x;
(2)∵点P的横坐标为m,
∴点P的纵坐标为:m2﹣2m,
令BC与x轴交点为M,过点P作PN⊥x轴,垂足为点N.
∵P是抛物线上位于第一象限内的一点,
∴PN=m2﹣2m,ON=m,OM=1,由=,得:=,
∴BM=m﹣2.
∵点C的坐标为(1,﹣1),
∴BC=m﹣2+1=m﹣1;
(3)令P(t,t2﹣2t).
∵△ABP的面积等于△ABC的面积,
∴AC=AP,过点P作PQ⊥BC交BC于点Q,
∴CM=MQ=1,可得:t2﹣2t=1,解得:t=1+(t=1﹣舍去),
∴P的坐标为(1+,1).
试卷第8页,共9页
试卷第9页,共9页
同课章节目录
