2021-2022学年北师大版八年级数学上册6.1 平均数同步练习 同步测试题(word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册6.1 平均数同步练习 同步测试题(word版含答案) |

|
|
| 格式 | docx | ||
| 文件大小 | 91.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 00:00:00 | ||
图片预览



文档简介
6.1 平均数同步练习同步测试题 2021-2022学年北师大版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
一组数据7,8,10,12,13的平均数是( )
A. B. C. D.
李明在本学期的前四次测验中数学成绩分别是95分、82分、76分、88分,马上要进行第五次测验了,他希望五次成绩的平均分能够达到85分,那么这次测验他应该达到( )
A. 分 B. 分 C. 分 D. 分
在数据1,2,3,4,a中添加5,不改变原数据的平均数,则a的值为( )
A. B. C. D.
为全力抗击新冠疫情,响应政府“停课不停学”号召,某市教育局发布关于疫情防控期间开展在线课程教学的通知:从2020年2月10日开始,全市中小学按照教学计划,开展在线课程教学和答疑.据互联网后台数据显示,某中学九年级七科老师2020年2月10日在线答疑问题总个数如下表:
学科 语文 数学 英语 物理 化学 道法 历史
数量/个 26 28 28 26 24 21 22
则2020年2月10日该中学九年级七科老师在线答疑问题总个数的平均数是( )
A. B. C. D.
已知数据x1,x2,x3的平均数是5,则数据3x1+2,3x2+2,3x3+2的平均数是( )
A. B. C. D.
某同学参加数学、物理、化学三科竞赛平均成绩是93分,其中数学97分,化学89分,那么物理成绩是()
A. 分 B. 分 C. 分 D. 分
如果x1与x2的平均数是6,那么x1+1与x2+3的平均数是( )
A. B. C. D.
在某人才招聘会上,组办方对应聘者进行了“听、说、读、写”四项技能测试,若人才要求是具有强的“听”力,较强的“说与“读“能力及基本的“写”能力,根据这个要求,听、说、读、写”四项技能测试比较合适的权重设计是( )
A. ::: B. ::: C. ::: D. :::
某居民小区10户家庭5月份的用水情况统计结果如表所示:
月用水量/m3 4 5 6 8 9
户数 2 3 3 1 1
这10户家庭的月平均用水量是( )
A. B. C. D.
面试时,某人的基本知识、表达能力、工作态度的得分分别是80分、70分、85分,若依次按30%、30%、40%的比例确定成绩,则这个人的面试成绩是( )
A. 分 B. 分 C. 分 D. 无法确定
二、填空题(本大题共7小题,共21分)
学校组织“我的中国梦”演讲比赛,每位选手的最后得分为去掉一个最低分、一个最高分后的平均数.7位评委给小红同学的打分分别是9.3,9.6,9.4,9.8,9.5,9.1,9.7,则小红同学的最后得分是 .
已知一组数据,,,,的平均数是8,则另一组数据+10,-10,+10,-10,+10的平均数为 .
一组数据7,x,8,y,10,z,6的平均数为4,则x,y,z的平均数是 .
5个数各减去200,所得到的差分别是8,6,-2,3, 0,则这5个数的平均数= .
已知a,b,c,d,e五个数的平均数是3,那么a+10,b+ 6, c+12,d+14,e+8五个数的平均数是 .
甲、乙、丙三种糖果售价分别为每千克6元,7元,8元,若将甲种5kg,乙种10kg,丙种10kg混在一起,则售价应定为每千克______.
学校“校园之声”广播站要选拔一名英语主持人,小莹参加选拔的各项成绩如下:
姓名 读 听 写
小莹 92分 80分 90分
若把读、听、写的成绩按5:3:2的比例计入个人的总分,则小莹的个人总分为 .
三、解答题(本大题共6小题,共69分)
如表给出了某班6名同学的身高情况:(单位:cm)
同学 A B C D E F
身高 165 ______ 166 ______ ______ 171
身高与班级平均身高的差值 -1 +2 ______ -3 +3 ______
(1)完成表中空白的部分;
(2)他们的最高身高与最矮身高相差多少?
(3)他们6人的平均身高是多少?
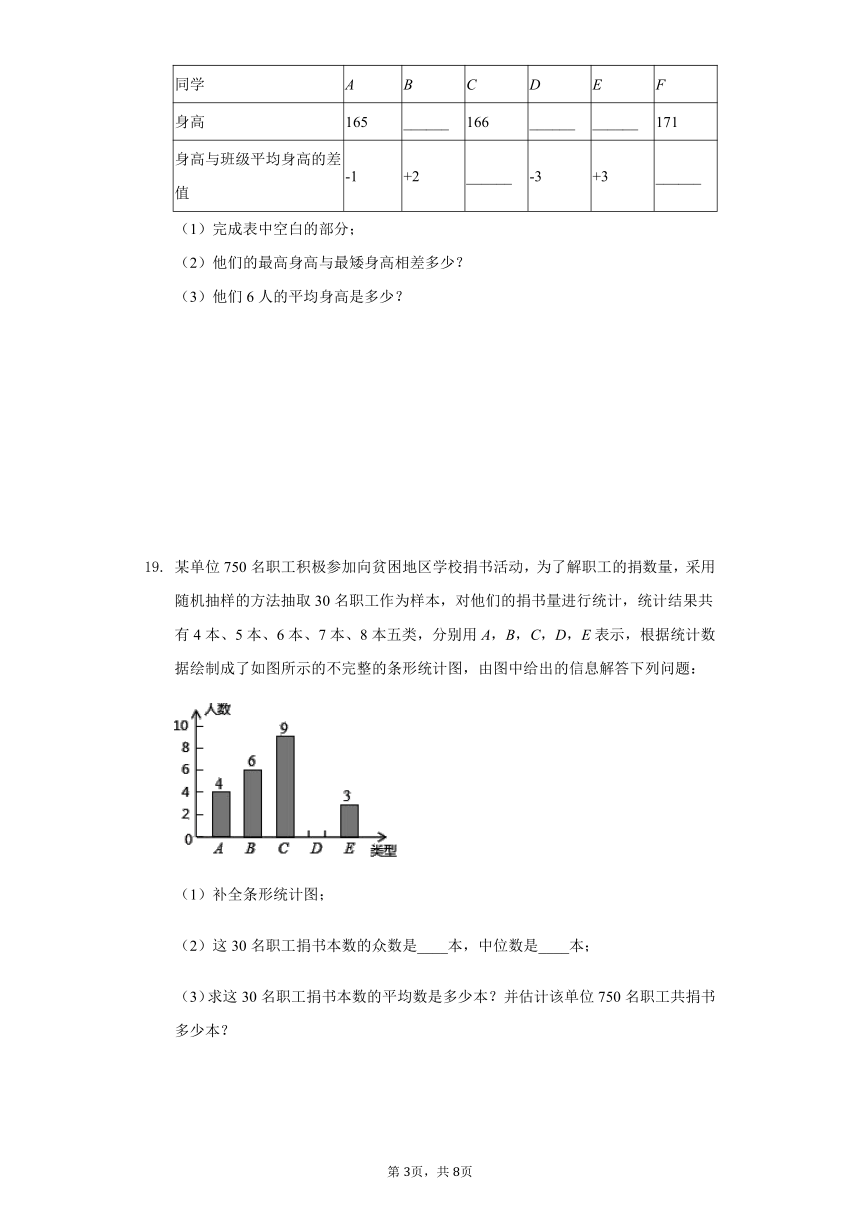
某单位750名职工积极参加向贫困地区学校捐书活动,为了解职工的捐数量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用A,B,C,D,E表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
(1)补全条形统计图;
(2)这30名职工捐书本数的众数是____本,中位数是____本;
(3)求这30名职工捐书本数的平均数是多少本?并估计该单位750名职工共捐书多少本?
为了改进银行的服务质量,随机抽查了30名顾客在窗口办理业务所用的时间(单位:分钟).下图是这次调查得到的统计图.请你根据图中的信息回答下列问题:
(1)办理业务所用的时间为11分钟的人数是____;
(2)补全条形统计图;
(3)这30名顾客办理业务所用时间的平均数是____分钟.
为增强学生预防新冠肺炎的安全意识,某校开展了疫情防控知识答题活动.为了解答题活动的得分情况(满分100分),随机抽取了部分参加答题活动的学生的成绩,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:
(1)图①中的m的值为_________;
(2)求该随机抽样获取的样本数据的平均数;
(3)若该校有360名学生参加了本次答题活动,估计其中获得满分的学生人数.
某公司欲招聘两名技术员,对甲、乙、丙三位候选人进行了笔试和面试,他们的成绩如下表所示:
候选人 甲 乙 丙
测试成
绩/分 笔试 86 92 90
面试 90 83 84
如果公司认为,作为技术人员笔试的成绩应该比面试的成绩更重要,并分别赋予它们7和3的权.根据三人各自的平均成绩,谁不能被录取
在实施城乡清洁工作过程中,某校对各个班级教室卫生情况进行考评,包括以下几项:黑板、门窗、桌椅、地面.一天,两个班级的各项卫生成绩分别如下表(单位:分):
黑板 门窗 桌椅 地面
一班 95 85 89 91
二班 90 95 85 90
(1)两个班的平均得分分别是多少
(2)按学校的考评要求,将黑板、门窗、桌椅、地面这四项得分依次按15%、10%、35%、40%的权重计算各班的卫生成绩,那么哪个班的卫生成绩较高 请说明理由.
1.【答案】C
2.【答案】A
3.【答案】D
4.【答案】C
5.【答案】D
6.【答案】C
7.【答案】D
8.【答案】A
9.【答案】C
10.【答案】B
11.【答案】 9.5
12.【答案】10
13.【答案】-1
14.【答案】203
15.【答案】13
16.【答案】7.2元
17.【答案】88
18.【答案】168 163 169 0 5
19.【答案】(1)补全图形见解析;(2)6,6;(3)6本;4500本.
20.【答案】(1)5;(2)见解析;(3)10.
21.【答案】解:(1)30;
(2)=93.2(分),
即随机抽样获取的样本数据的平均数为93.2;
(3)36010%=36(人),
即估计其中获得满分的学生有36人.
22.【答案】解:甲的平均成绩为,
乙的平均成绩为,
丙的平均成绩为,
由于87.2<88.2<89.3,
所以甲不能被录取.
23.【答案】解:(1)一班的平均得分为(95+85+89+91)4=90(分),
二班的平均得分为(90+95+85+90)4=90(分).
(2)一班的卫生成绩较高.
理由:一班的加权平均成绩为9515%+8510%+8935%+9140%=90.3(分),
二班的加权平均成绩为9015% +9510%+8535%+9040%=88.75(分).
因为90.3>88.75,所以一班的卫生成绩较高.
第1页,共1页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共10小题,共30分)
一组数据7,8,10,12,13的平均数是( )
A. B. C. D.
李明在本学期的前四次测验中数学成绩分别是95分、82分、76分、88分,马上要进行第五次测验了,他希望五次成绩的平均分能够达到85分,那么这次测验他应该达到( )
A. 分 B. 分 C. 分 D. 分
在数据1,2,3,4,a中添加5,不改变原数据的平均数,则a的值为( )
A. B. C. D.
为全力抗击新冠疫情,响应政府“停课不停学”号召,某市教育局发布关于疫情防控期间开展在线课程教学的通知:从2020年2月10日开始,全市中小学按照教学计划,开展在线课程教学和答疑.据互联网后台数据显示,某中学九年级七科老师2020年2月10日在线答疑问题总个数如下表:
学科 语文 数学 英语 物理 化学 道法 历史
数量/个 26 28 28 26 24 21 22
则2020年2月10日该中学九年级七科老师在线答疑问题总个数的平均数是( )
A. B. C. D.
已知数据x1,x2,x3的平均数是5,则数据3x1+2,3x2+2,3x3+2的平均数是( )
A. B. C. D.
某同学参加数学、物理、化学三科竞赛平均成绩是93分,其中数学97分,化学89分,那么物理成绩是()
A. 分 B. 分 C. 分 D. 分
如果x1与x2的平均数是6,那么x1+1与x2+3的平均数是( )
A. B. C. D.
在某人才招聘会上,组办方对应聘者进行了“听、说、读、写”四项技能测试,若人才要求是具有强的“听”力,较强的“说与“读“能力及基本的“写”能力,根据这个要求,听、说、读、写”四项技能测试比较合适的权重设计是( )
A. ::: B. ::: C. ::: D. :::
某居民小区10户家庭5月份的用水情况统计结果如表所示:
月用水量/m3 4 5 6 8 9
户数 2 3 3 1 1
这10户家庭的月平均用水量是( )
A. B. C. D.
面试时,某人的基本知识、表达能力、工作态度的得分分别是80分、70分、85分,若依次按30%、30%、40%的比例确定成绩,则这个人的面试成绩是( )
A. 分 B. 分 C. 分 D. 无法确定
二、填空题(本大题共7小题,共21分)
学校组织“我的中国梦”演讲比赛,每位选手的最后得分为去掉一个最低分、一个最高分后的平均数.7位评委给小红同学的打分分别是9.3,9.6,9.4,9.8,9.5,9.1,9.7,则小红同学的最后得分是 .
已知一组数据,,,,的平均数是8,则另一组数据+10,-10,+10,-10,+10的平均数为 .
一组数据7,x,8,y,10,z,6的平均数为4,则x,y,z的平均数是 .
5个数各减去200,所得到的差分别是8,6,-2,3, 0,则这5个数的平均数= .
已知a,b,c,d,e五个数的平均数是3,那么a+10,b+ 6, c+12,d+14,e+8五个数的平均数是 .
甲、乙、丙三种糖果售价分别为每千克6元,7元,8元,若将甲种5kg,乙种10kg,丙种10kg混在一起,则售价应定为每千克______.
学校“校园之声”广播站要选拔一名英语主持人,小莹参加选拔的各项成绩如下:
姓名 读 听 写
小莹 92分 80分 90分
若把读、听、写的成绩按5:3:2的比例计入个人的总分,则小莹的个人总分为 .
三、解答题(本大题共6小题,共69分)
如表给出了某班6名同学的身高情况:(单位:cm)
同学 A B C D E F
身高 165 ______ 166 ______ ______ 171
身高与班级平均身高的差值 -1 +2 ______ -3 +3 ______
(1)完成表中空白的部分;
(2)他们的最高身高与最矮身高相差多少?
(3)他们6人的平均身高是多少?
某单位750名职工积极参加向贫困地区学校捐书活动,为了解职工的捐数量,采用随机抽样的方法抽取30名职工作为样本,对他们的捐书量进行统计,统计结果共有4本、5本、6本、7本、8本五类,分别用A,B,C,D,E表示,根据统计数据绘制成了如图所示的不完整的条形统计图,由图中给出的信息解答下列问题:
(1)补全条形统计图;
(2)这30名职工捐书本数的众数是____本,中位数是____本;
(3)求这30名职工捐书本数的平均数是多少本?并估计该单位750名职工共捐书多少本?
为了改进银行的服务质量,随机抽查了30名顾客在窗口办理业务所用的时间(单位:分钟).下图是这次调查得到的统计图.请你根据图中的信息回答下列问题:
(1)办理业务所用的时间为11分钟的人数是____;
(2)补全条形统计图;
(3)这30名顾客办理业务所用时间的平均数是____分钟.
为增强学生预防新冠肺炎的安全意识,某校开展了疫情防控知识答题活动.为了解答题活动的得分情况(满分100分),随机抽取了部分参加答题活动的学生的成绩,并用得到的数据绘制了统计图①和图②,请根据图中提供的信息,回答下列问题:
(1)图①中的m的值为_________;
(2)求该随机抽样获取的样本数据的平均数;
(3)若该校有360名学生参加了本次答题活动,估计其中获得满分的学生人数.
某公司欲招聘两名技术员,对甲、乙、丙三位候选人进行了笔试和面试,他们的成绩如下表所示:
候选人 甲 乙 丙
测试成
绩/分 笔试 86 92 90
面试 90 83 84
如果公司认为,作为技术人员笔试的成绩应该比面试的成绩更重要,并分别赋予它们7和3的权.根据三人各自的平均成绩,谁不能被录取
在实施城乡清洁工作过程中,某校对各个班级教室卫生情况进行考评,包括以下几项:黑板、门窗、桌椅、地面.一天,两个班级的各项卫生成绩分别如下表(单位:分):
黑板 门窗 桌椅 地面
一班 95 85 89 91
二班 90 95 85 90
(1)两个班的平均得分分别是多少
(2)按学校的考评要求,将黑板、门窗、桌椅、地面这四项得分依次按15%、10%、35%、40%的权重计算各班的卫生成绩,那么哪个班的卫生成绩较高 请说明理由.
1.【答案】C
2.【答案】A
3.【答案】D
4.【答案】C
5.【答案】D
6.【答案】C
7.【答案】D
8.【答案】A
9.【答案】C
10.【答案】B
11.【答案】 9.5
12.【答案】10
13.【答案】-1
14.【答案】203
15.【答案】13
16.【答案】7.2元
17.【答案】88
18.【答案】168 163 169 0 5
19.【答案】(1)补全图形见解析;(2)6,6;(3)6本;4500本.
20.【答案】(1)5;(2)见解析;(3)10.
21.【答案】解:(1)30;
(2)=93.2(分),
即随机抽样获取的样本数据的平均数为93.2;
(3)36010%=36(人),
即估计其中获得满分的学生有36人.
22.【答案】解:甲的平均成绩为,
乙的平均成绩为,
丙的平均成绩为,
由于87.2<88.2<89.3,
所以甲不能被录取.
23.【答案】解:(1)一班的平均得分为(95+85+89+91)4=90(分),
二班的平均得分为(90+95+85+90)4=90(分).
(2)一班的卫生成绩较高.
理由:一班的加权平均成绩为9515%+8510%+8935%+9140%=90.3(分),
二班的加权平均成绩为9015% +9510%+8535%+9040%=88.75(分).
因为90.3>88.75,所以一班的卫生成绩较高.
第1页,共1页
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
