2021--2022学年人教版九年级数学上册24.1.2 -垂径定理的应用训练(word版含答案)
文档属性
| 名称 | 2021--2022学年人教版九年级数学上册24.1.2 -垂径定理的应用训练(word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 972.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 10:48:32 | ||
图片预览

文档简介
人教版九年级上册数学24章圆-垂径定理的应用训练
一、单选题
1.如图,已知BD是⊙O的直径,BD⊥AC于点E,∠AOC=100°,则∠BDC的度数是( )
A.20° B.25° C.30° D.40°
2.筒车是我国古代发明的一种水利灌溉工具,如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且被水面截得的弦长为6米,半径长为4米.若点C为运行轨道的最低点,则点C到弦所在直线的距离是( )
A.1米 B.米 C.2米 D.米
3.如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果水的最大深度CD为2dm,水面宽AB为8dm,则输水管的直径为( )
A. B. C. D.
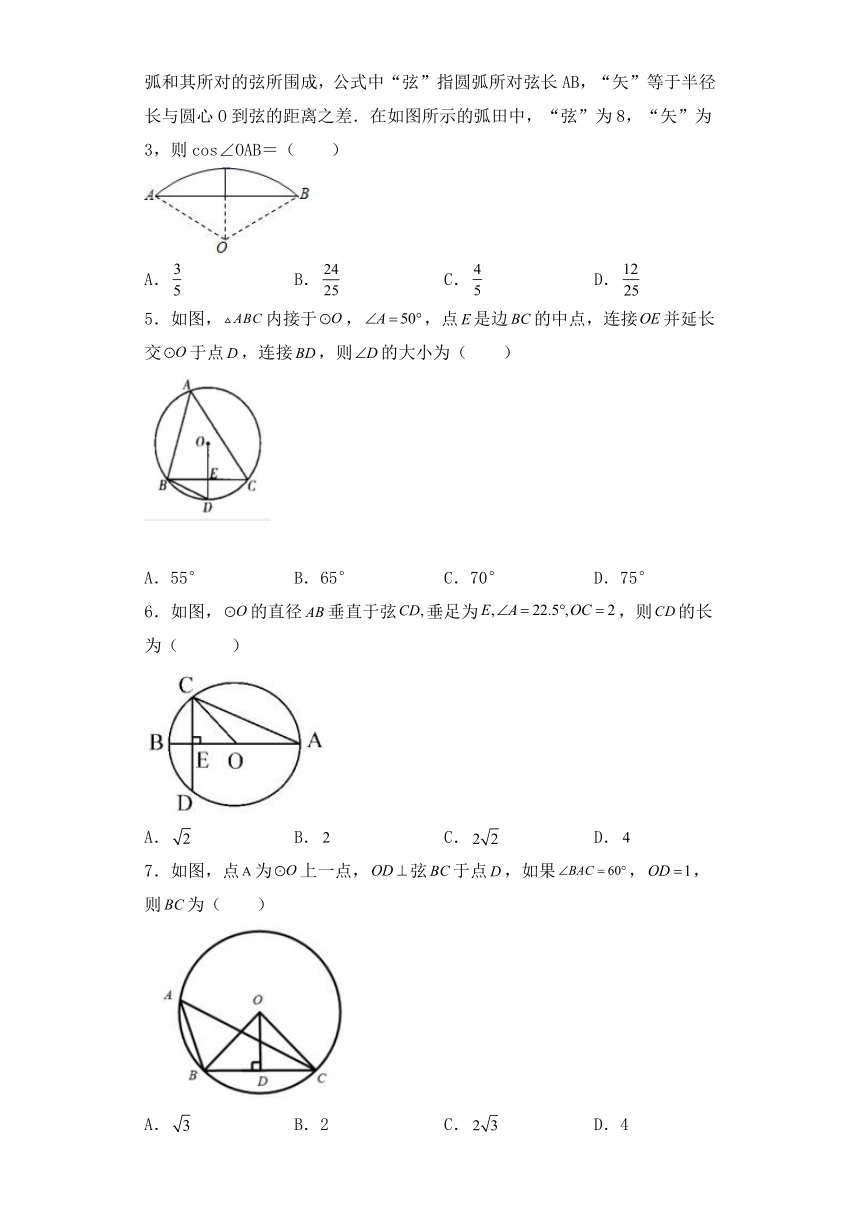
4.《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积所用公式为:弧田面积=(弦×矢+矢2),弧田(如图)是由圆弧和其所对的弦所围成,公式中“弦”指圆弧所对弦长AB,“矢”等于半径长与圆心O到弦的距离之差.在如图所示的弧田中,“弦”为8,“矢”为3,则cos∠OAB=( )
A. B. C. D.
5.如图,内接于,,点是边的中点,连接并延长交于点,连接,则的大小为( )
A.55° B.65° C.70° D.75°
6.如图,的直径垂直于弦垂足为,则的长为( )
A. B. C. D.
7.如图,点为上一点,弦于点,如果,,则为( )
A. B.2 C. D.4
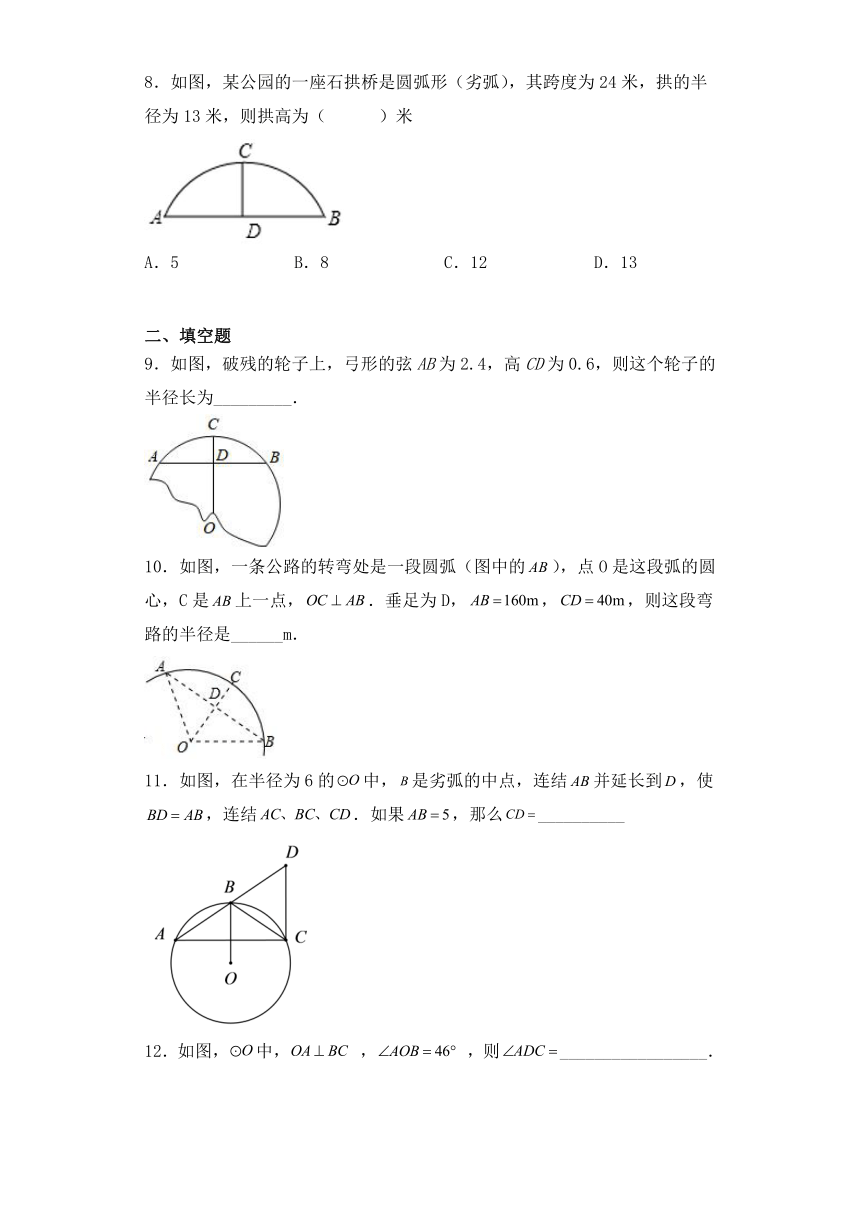
8.如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为( )米
A.5 B.8 C.12 D.13
二、填空题
9.如图,破残的轮子上,弓形的弦AB为2.4,高CD为0.6,则这个轮子的半径长为_________.
10.如图,一条公路的转弯处是一段圆弧(图中的),点O是这段弧的圆心,C是上一点,.垂足为D,,,则这段弯路的半径是______m.
11.如图,在半径为6的中,是劣弧的中点,连结并延长到,使,连结.如果,那么__________
12.如图,中, , ,则_________________.
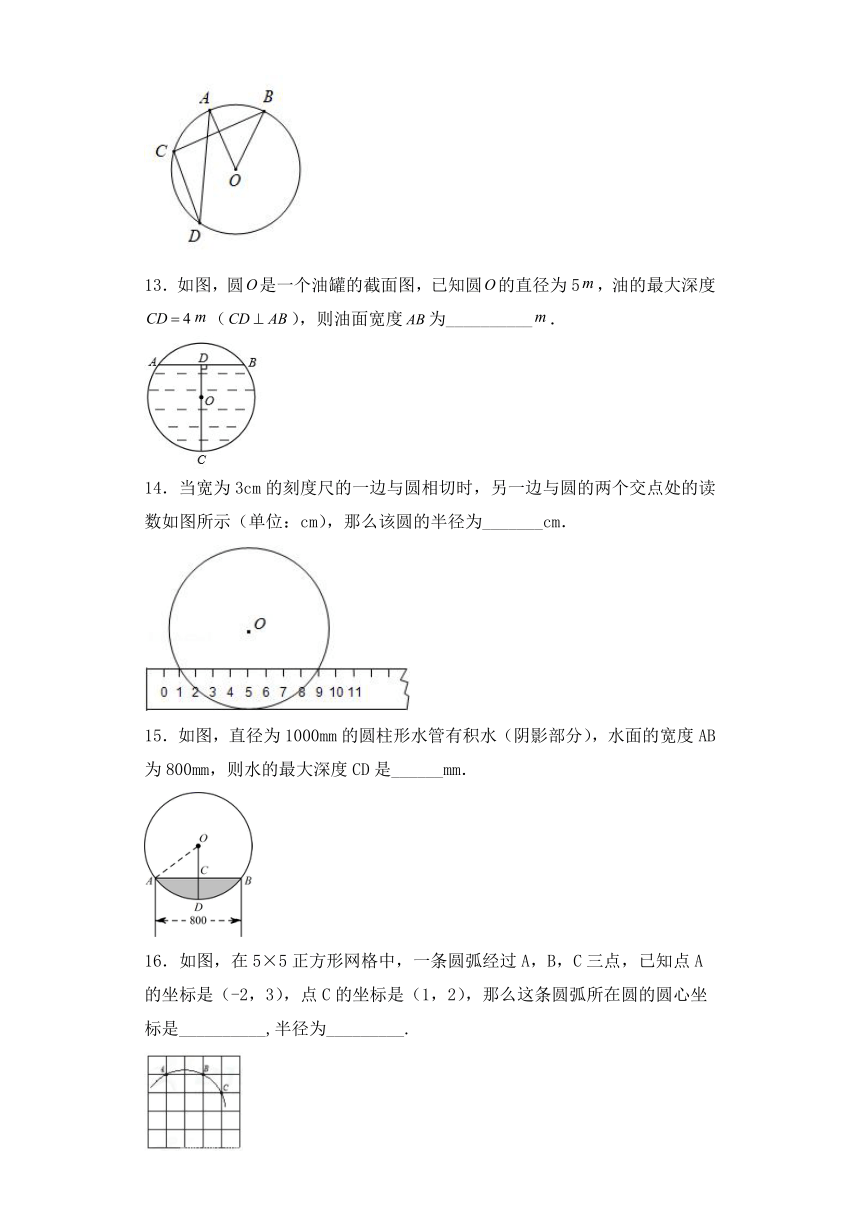
13.如图,圆是一个油罐的截面图,已知圆的直径为5,油的最大深度(),则油面宽度为__________.
14.当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm),那么该圆的半径为_______cm.
15.如图,直径为1000mm的圆柱形水管有积水(阴影部分),水面的宽度AB为800mm,则水的最大深度CD是______mm.
16.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(-2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是__________,半径为_________.
三、解答题
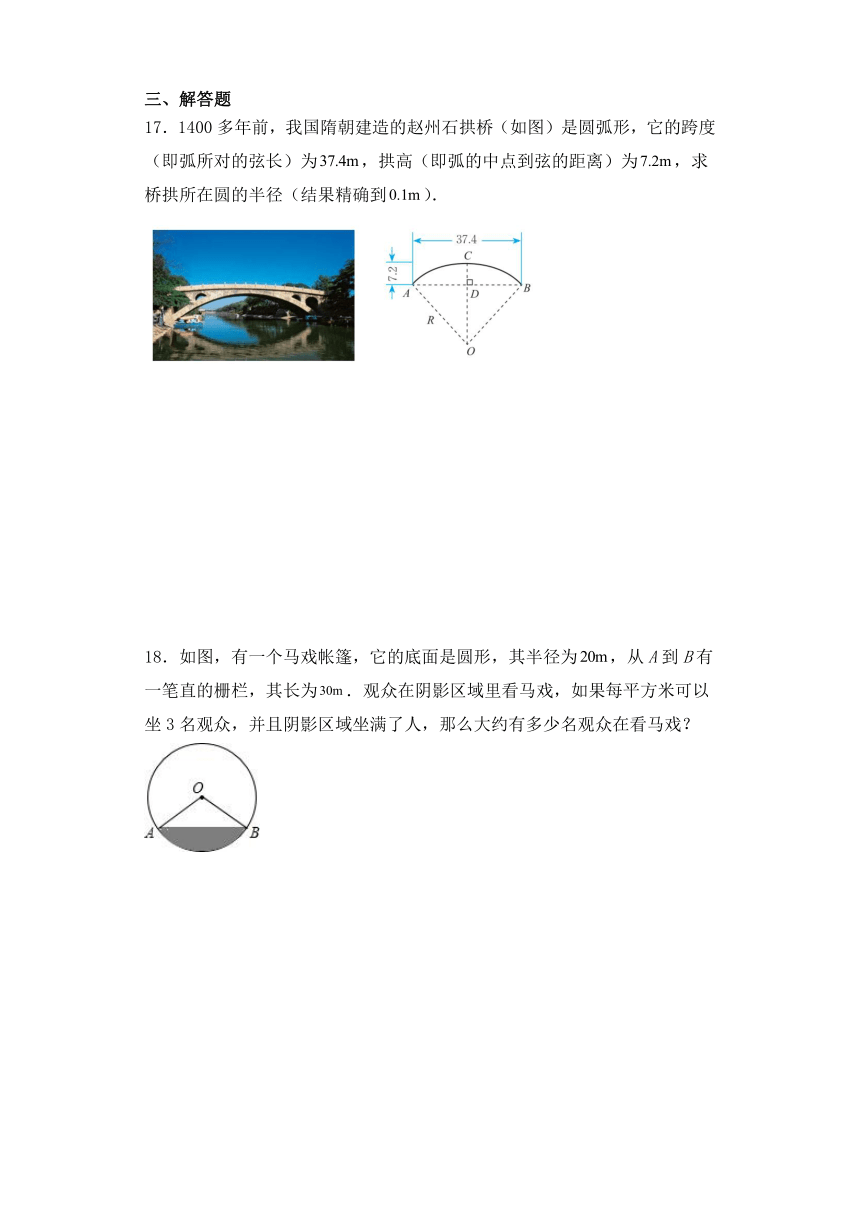
17.1400多年前,我国隋朝建造的赵州石拱桥(如图)是圆弧形,它的跨度(即弧所对的弦长)为,拱高(即弧的中点到弦的距离)为,求桥拱所在圆的半径(结果精确到).
18.如图,有一个马戏帐篷,它的底面是圆形,其半径为,从A到B有一笔直的栅栏,其长为.观众在阴影区域里看马戏,如果每平方米可以坐3名观众,并且阴影区域坐满了人,那么大约有多少名观众在看马戏?
19.如图,水平放置的圆柱形排水管道的截面半径是,其中水面高.求截面上有水部分的面积(结果保留小数点后两位).
20.如图所示,某地欲搭建一座圆弧型拱桥,跨度AB=32米,拱高CD=8米(C为AB的中点,D为弧AB的中点).
(1)求该圆弧所在圆的半径;
(2)在距离桥的一端4米处欲立一桥墩EF支撑,求桥墩的高度.
参考答案
1.B
解:∵BO⊥AC,∠AOC=100°,
∴∠BOC=∠AOC=50°,
则∠BDC=∠BOC=25°,
故选:B.
2.B
解:连接OC交AB于D,连接OA,
是运行轨道最低点
(米)
中,(米)
则点C到弦所在直线的距离是(米)
故选:B.
3.D
解:根据题意可知: , , ,
∴,
设圆的半径 ,则,
在 中, ,
即 ,解得: ,
∴输水管的直径为 .
故选:D
4.B
解:如图,作OH⊥AB于H.交圆弧于C,
由题意:AB=8,HC=3,
∴OA﹣OH=3,
∵OH⊥AB,OC为半径,
∴AH=BH==4,
在Rt△OAH中
由勾股定理得AH2+OH2=OA2,
∴42=(OA+OH)(OA﹣OH),
∴OA+OH=,
∴OA=,OH=,
∴cos∠OAB=,
故选:B.
5.B
如图:连接CD,
∵ ∠A=50°,
∴∠CDB=180°-∠A=130°,
∵ E是边BC的中点,
∴ OD⊥BC,
∴ BD=CD,
∴ ∠ODB=∠ODC=∠BDC=65°,
故选:B.
6.C
解:∵⊙O的直径AB垂直于弦CD,
∴CD=2CE,∠CEO=90°,
又∵∠COE=2∠A=45°,
∴△CEO为等腰直角三角形,
∴CE=OC=,
∴CD=2CE=.
故选:C.
7.C
解:由图可得∠BOC=2∠BAC=2×60°=120°,
∵OB=OC,
∴∠OBC=∠OCB=30°,
∵,
∴BD=CD,
在Rt中,BD=OD=,
∴BC=2BD=2.
故选:C.
8.B
解:因为跨度AB=24m,拱的半径为13m,延长CD到O,使得OC=OB,则O为圆心,则BD=,
又∵OB=13,
在Rt△BOD中,DO=
∴拱高CD=CO-DO=13-5=8米.
故选B.
9.1.5
解:连接OB,如图所示:
由题意得:OC⊥AB,
∴AD=BD=AB=1.2,
在Rt△OBD中,根据勾股定理得: ,
即 ,
解得:OB=1.5,
即这个轮子的半径长为1.5,
故答案为:1.5.
10.
解:设这段弯路的半径是rm,,
则OA=OC=rm,,
∵OC⊥AB,
∴,
在Rt△AOD中,
由勾股定理得:
,
解得:,
则这段弯路的半径是100m.
故答案为:.
11..
【分析】
解:如图,连OA,OB,
∵B是弧AC的中点,AB=BC=BD,
∴△ACD是直角三角形,∠ACD=90 ,
由垂径定理知,OB⊥AC,点E是AC的中点,
由勾股定理知,,
∵AB=5,AO=BO=6,代入解得,BE=,
∵∠AEB=∠ACD=90 ,
∴BE∥CD,
∵点B是AD的中点,所以BE是△ACD的中位线,所以CD=2BE=.
12.23°
解:连接OC,如图所示:
∵,OA为半径,
∴,
∴∠AOC=∠AOB,
∵,
∴∠AOC=46°,
∴∠ADC=;
故答案为23°.
13.4
解:连接OA
∵圆的直径为5,油的最大深度
∴OA=OC=
∴OD=CD-OC=
∵
根据勾股定理可得:AD=
∴AB=2AD=4m
故答案为:4.
14..
【详解】
如图,连接OA,过点O作OD⊥AB于点D,
∵OD⊥AB,∴AD=AB=(9﹣1)=4.
设OA=r,则OD=r﹣3,
在Rt△OAD中,
OA2﹣OD2=AD2,即r2﹣(r﹣3)2=42,解得r=(cm).
15.200
解:∵⊙O的直径为1000mm,
∴OA=OA=500mm.
∵OD⊥AB,AB=800mm,
∴AC=400mm,
∴OC== =300mm,
∴CD=OD-OC=500-300=200(mm).
答:水的最大深度为200mm.
故答案为:200
16.(-1,1)
如图线段AB的垂直平分线和线段CD的垂直平分线的交点M,
即圆心的坐标是(-1,1),
根据勾股定理可得半径为:.故答案为(1). (-1,1) (2). .
17..
解:如图,∵,拱桥的跨度AB=37.4m,拱高CD=7.2m,
∴AD=AB=18.7m,
∴AD2=OA2 (OC CD)2,即18.72=AO2 (AO 7.2)2,
解得AO≈27.9m.即圆弧半径为27.9m.
答:桥拱所在圆的半径为27.9m.
18.约421人.
解:过O作OD⊥AB,D为垂足,
∵AB=30m.
∴AD=BD=15m,
∴OD==5
∵sin∠AOD===0.75,
∴∠AOD≈49°,
∴∠AOB=98°,
∴S阴影部分=S扇形OAB-S△OAB=-×30×5≈145.7m2,
∴145.7×3≈437(人).
答:大约有437位观众在看马戏.
19.
解:如图,连接,作弦的垂直平分线,垂足为D,交于点C,连接.
,
.
.
又,
是线段的垂直平分线.
.
从而.
,
,
有水部分的面积,
,
,
.
20.(1)20米;(2)4米
解:(1)设弧AB所在的圆心为O,C为弧AB的中点,CD⊥AB于D,延长CD经过O点,设⊙O的半径为R,
在Rt△OBD中,OB2=OD2+DB2,
∴R2=(R﹣8)2+162,
解得R=20;
(2)在圆弧型中设点F′在弧AB上,作F′E′⊥AB于E′,
OH⊥F′E′于H,则OH=DE′=16﹣4=12,OF′=R=20,
在Rt△OHF′中,HF′=,
∵HE′=OD=OC﹣CD=20﹣8=12,E′F′=HF′﹣HE′=16﹣12=4(米),
∴在离桥的一端4米处,圆弧型桥墩高4米.
一、单选题
1.如图,已知BD是⊙O的直径,BD⊥AC于点E,∠AOC=100°,则∠BDC的度数是( )
A.20° B.25° C.30° D.40°
2.筒车是我国古代发明的一种水利灌溉工具,如图1,筒车盛水桶的运行轨道是以轴心O为圆心的圆,如图2.已知圆心O在水面上方,且被水面截得的弦长为6米,半径长为4米.若点C为运行轨道的最低点,则点C到弦所在直线的距离是( )
A.1米 B.米 C.2米 D.米
3.如图表示一圆柱形输水管的横截面,阴影部分为有水部分,如果水的最大深度CD为2dm,水面宽AB为8dm,则输水管的直径为( )
A. B. C. D.
4.《九章算术》是我国古代数学成就的杰出代表,其中《方田》章给出计算弧田面积所用公式为:弧田面积=(弦×矢+矢2),弧田(如图)是由圆弧和其所对的弦所围成,公式中“弦”指圆弧所对弦长AB,“矢”等于半径长与圆心O到弦的距离之差.在如图所示的弧田中,“弦”为8,“矢”为3,则cos∠OAB=( )
A. B. C. D.
5.如图,内接于,,点是边的中点,连接并延长交于点,连接,则的大小为( )
A.55° B.65° C.70° D.75°
6.如图,的直径垂直于弦垂足为,则的长为( )
A. B. C. D.
7.如图,点为上一点,弦于点,如果,,则为( )
A. B.2 C. D.4
8.如图,某公园的一座石拱桥是圆弧形(劣弧),其跨度为24米,拱的半径为13米,则拱高为( )米
A.5 B.8 C.12 D.13
二、填空题
9.如图,破残的轮子上,弓形的弦AB为2.4,高CD为0.6,则这个轮子的半径长为_________.
10.如图,一条公路的转弯处是一段圆弧(图中的),点O是这段弧的圆心,C是上一点,.垂足为D,,,则这段弯路的半径是______m.
11.如图,在半径为6的中,是劣弧的中点,连结并延长到,使,连结.如果,那么__________
12.如图,中, , ,则_________________.
13.如图,圆是一个油罐的截面图,已知圆的直径为5,油的最大深度(),则油面宽度为__________.
14.当宽为3cm的刻度尺的一边与圆相切时,另一边与圆的两个交点处的读数如图所示(单位:cm),那么该圆的半径为_______cm.
15.如图,直径为1000mm的圆柱形水管有积水(阴影部分),水面的宽度AB为800mm,则水的最大深度CD是______mm.
16.如图,在5×5正方形网格中,一条圆弧经过A,B,C三点,已知点A的坐标是(-2,3),点C的坐标是(1,2),那么这条圆弧所在圆的圆心坐标是__________,半径为_________.
三、解答题
17.1400多年前,我国隋朝建造的赵州石拱桥(如图)是圆弧形,它的跨度(即弧所对的弦长)为,拱高(即弧的中点到弦的距离)为,求桥拱所在圆的半径(结果精确到).
18.如图,有一个马戏帐篷,它的底面是圆形,其半径为,从A到B有一笔直的栅栏,其长为.观众在阴影区域里看马戏,如果每平方米可以坐3名观众,并且阴影区域坐满了人,那么大约有多少名观众在看马戏?
19.如图,水平放置的圆柱形排水管道的截面半径是,其中水面高.求截面上有水部分的面积(结果保留小数点后两位).
20.如图所示,某地欲搭建一座圆弧型拱桥,跨度AB=32米,拱高CD=8米(C为AB的中点,D为弧AB的中点).
(1)求该圆弧所在圆的半径;
(2)在距离桥的一端4米处欲立一桥墩EF支撑,求桥墩的高度.
参考答案
1.B
解:∵BO⊥AC,∠AOC=100°,
∴∠BOC=∠AOC=50°,
则∠BDC=∠BOC=25°,
故选:B.
2.B
解:连接OC交AB于D,连接OA,
是运行轨道最低点
(米)
中,(米)
则点C到弦所在直线的距离是(米)
故选:B.
3.D
解:根据题意可知: , , ,
∴,
设圆的半径 ,则,
在 中, ,
即 ,解得: ,
∴输水管的直径为 .
故选:D
4.B
解:如图,作OH⊥AB于H.交圆弧于C,
由题意:AB=8,HC=3,
∴OA﹣OH=3,
∵OH⊥AB,OC为半径,
∴AH=BH==4,
在Rt△OAH中
由勾股定理得AH2+OH2=OA2,
∴42=(OA+OH)(OA﹣OH),
∴OA+OH=,
∴OA=,OH=,
∴cos∠OAB=,
故选:B.
5.B
如图:连接CD,
∵ ∠A=50°,
∴∠CDB=180°-∠A=130°,
∵ E是边BC的中点,
∴ OD⊥BC,
∴ BD=CD,
∴ ∠ODB=∠ODC=∠BDC=65°,
故选:B.
6.C
解:∵⊙O的直径AB垂直于弦CD,
∴CD=2CE,∠CEO=90°,
又∵∠COE=2∠A=45°,
∴△CEO为等腰直角三角形,
∴CE=OC=,
∴CD=2CE=.
故选:C.
7.C
解:由图可得∠BOC=2∠BAC=2×60°=120°,
∵OB=OC,
∴∠OBC=∠OCB=30°,
∵,
∴BD=CD,
在Rt中,BD=OD=,
∴BC=2BD=2.
故选:C.
8.B
解:因为跨度AB=24m,拱的半径为13m,延长CD到O,使得OC=OB,则O为圆心,则BD=,
又∵OB=13,
在Rt△BOD中,DO=
∴拱高CD=CO-DO=13-5=8米.
故选B.
9.1.5
解:连接OB,如图所示:
由题意得:OC⊥AB,
∴AD=BD=AB=1.2,
在Rt△OBD中,根据勾股定理得: ,
即 ,
解得:OB=1.5,
即这个轮子的半径长为1.5,
故答案为:1.5.
10.
解:设这段弯路的半径是rm,,
则OA=OC=rm,,
∵OC⊥AB,
∴,
在Rt△AOD中,
由勾股定理得:
,
解得:,
则这段弯路的半径是100m.
故答案为:.
11..
【分析】
解:如图,连OA,OB,
∵B是弧AC的中点,AB=BC=BD,
∴△ACD是直角三角形,∠ACD=90 ,
由垂径定理知,OB⊥AC,点E是AC的中点,
由勾股定理知,,
∵AB=5,AO=BO=6,代入解得,BE=,
∵∠AEB=∠ACD=90 ,
∴BE∥CD,
∵点B是AD的中点,所以BE是△ACD的中位线,所以CD=2BE=.
12.23°
解:连接OC,如图所示:
∵,OA为半径,
∴,
∴∠AOC=∠AOB,
∵,
∴∠AOC=46°,
∴∠ADC=;
故答案为23°.
13.4
解:连接OA
∵圆的直径为5,油的最大深度
∴OA=OC=
∴OD=CD-OC=
∵
根据勾股定理可得:AD=
∴AB=2AD=4m
故答案为:4.
14..
【详解】
如图,连接OA,过点O作OD⊥AB于点D,
∵OD⊥AB,∴AD=AB=(9﹣1)=4.
设OA=r,则OD=r﹣3,
在Rt△OAD中,
OA2﹣OD2=AD2,即r2﹣(r﹣3)2=42,解得r=(cm).
15.200
解:∵⊙O的直径为1000mm,
∴OA=OA=500mm.
∵OD⊥AB,AB=800mm,
∴AC=400mm,
∴OC== =300mm,
∴CD=OD-OC=500-300=200(mm).
答:水的最大深度为200mm.
故答案为:200
16.(-1,1)
如图线段AB的垂直平分线和线段CD的垂直平分线的交点M,
即圆心的坐标是(-1,1),
根据勾股定理可得半径为:.故答案为(1). (-1,1) (2). .
17..
解:如图,∵,拱桥的跨度AB=37.4m,拱高CD=7.2m,
∴AD=AB=18.7m,
∴AD2=OA2 (OC CD)2,即18.72=AO2 (AO 7.2)2,
解得AO≈27.9m.即圆弧半径为27.9m.
答:桥拱所在圆的半径为27.9m.
18.约421人.
解:过O作OD⊥AB,D为垂足,
∵AB=30m.
∴AD=BD=15m,
∴OD==5
∵sin∠AOD===0.75,
∴∠AOD≈49°,
∴∠AOB=98°,
∴S阴影部分=S扇形OAB-S△OAB=-×30×5≈145.7m2,
∴145.7×3≈437(人).
答:大约有437位观众在看马戏.
19.
解:如图,连接,作弦的垂直平分线,垂足为D,交于点C,连接.
,
.
.
又,
是线段的垂直平分线.
.
从而.
,
,
有水部分的面积,
,
,
.
20.(1)20米;(2)4米
解:(1)设弧AB所在的圆心为O,C为弧AB的中点,CD⊥AB于D,延长CD经过O点,设⊙O的半径为R,
在Rt△OBD中,OB2=OD2+DB2,
∴R2=(R﹣8)2+162,
解得R=20;
(2)在圆弧型中设点F′在弧AB上,作F′E′⊥AB于E′,
OH⊥F′E′于H,则OH=DE′=16﹣4=12,OF′=R=20,
在Rt△OHF′中,HF′=,
∵HE′=OD=OC﹣CD=20﹣8=12,E′F′=HF′﹣HE′=16﹣12=4(米),
∴在离桥的一端4米处,圆弧型桥墩高4米.
同课章节目录
