六年级数学下册课件 - 正反比例的练习 苏教版(共21张PPT)
文档属性
| 名称 | 六年级数学下册课件 - 正反比例的练习 苏教版(共21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 903.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 06:37:04 | ||
图片预览







文档简介
(共21张PPT)
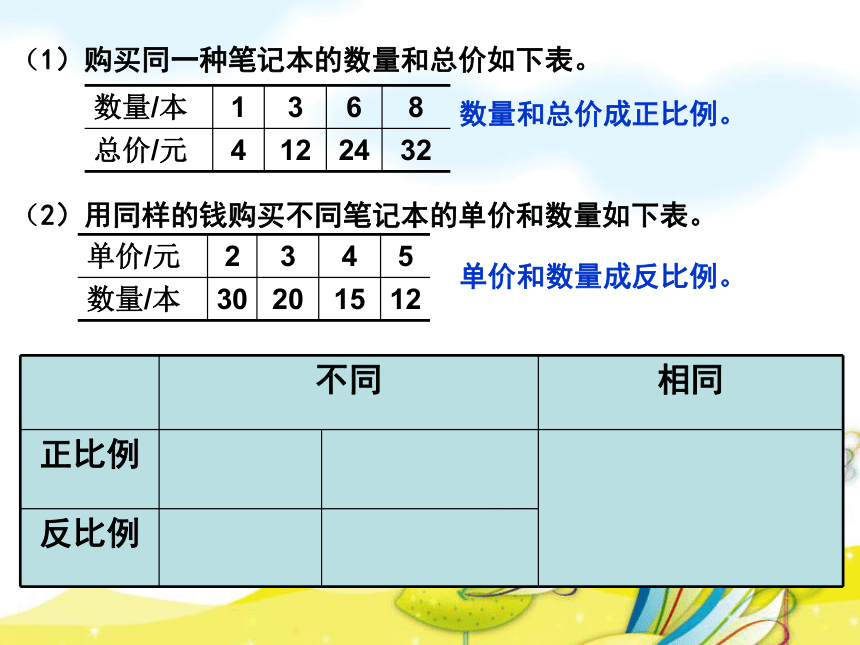
数量/本 1 3 6 8
总价/元 4 12 24 32
单价/元 2 3 4 5
数量/本 30 20 15 12
(1)购买同一种笔记本的数量和总价如下表。
(2)用同样的钱购买不同笔记本的单价和数量如下表。
判断下列各题中的两种量是什么比例关系,并说明理由。
数量/本 1 3 6 8
总价/元 4 12 24 32
单价/元 2 3 4 5
数量/本 30 20 15 12
(1)购买同一种笔记本的数量和总价如下表。
数量和总价成正比例。
总价÷数量=单价(一定)
(2)用同样的钱购买不同笔记本的单价和数量如下表。
单价和数量成反比例。
单价×数量=总价(一定)
数量/本 1 3 6 8
总价/元 4 12 24 32
单价/元 2 3 4 5
数量/本 30 20 15 12
(1)购买同一种笔记本的数量和总价如下表。
(2)用同样的钱购买不同笔记本的单价和数量如下表。
数量和总价成正比例。
单价和数量成反比例。
不同 相同
正比例
反比例
数量/本 1 3 6 8
总价/元 4 12 24 32
单价/元 2 3 4 5
数量/本 30 20 15 12
(1)购买同一种笔记本的数量和总价如下表。
(2)用同样的钱购买不同笔记本的单价和数量如下表。
如果购买笔记本的数量一定,
笔记本的单价和总价成( )比例。
正
数量/本 1 3 6 8
总价/元 4 12 24 32
单价/元 2 3 4 5
数量/本 30 20 15 12
(1)购买同一种笔记本的数量和总价如下表。
(2)用同样的钱购买不同笔记本的单价和数量如下表。
如果购买笔记本的数量一定,
笔记本的单价和总价成( )比例。
正
数量和单价成反比例
数量和总价成正比例
总价和单价成正比例
单价一定
总价一定
数量一定
数量和单价成反比例
数量和总价成正比例
总价和单价成正比例
单价一定
总价一定
数量一定
比值一定
乘积一定
你还能举出这样类似的例子吗?
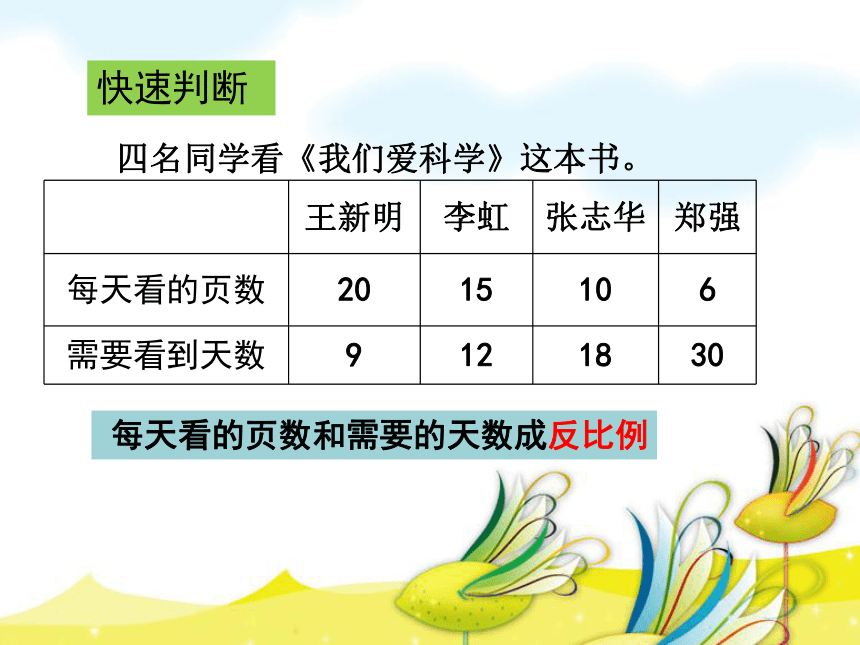
快速判断
四名同学看《我们爱科学》这本书。
王新明 李虹 张志华 郑强
每天看的页数 20 15 10 6
需要看到天数 9 12 18 30
每天看的页数和需要的天数成反比例
快速判断
图上距离和实际距离成正比例
快速判断
跳绳的时间和总个数成正比例
每分钟跳绳的个数是一定的,
跳绳的时间和总个数。
总个数÷跳绳的时间=每分钟跳绳的个数(一定)
快速判断
地砖的面积和地砖的数量反比例
给一个房间的地面铺地砖,
地砖的面积和地砖的数量。
地砖的数量×地砖的面积=房间的面积(一定)
快速判断
人的身高和体重不成比例
人的身高和体重
快速判断
已经修的长度和还剩的长度不成比例
修一条公路,已经修的长度和还剩的长度。
已经修到长度+还剩的程度=公路全长(一定)
快速判断
圆的直径和周长正比例
圆的直径和周长
圆的周长÷直径=圆周率(一定)
快速判断
正方形边长和面积不成比例
正方形边长和面积
正方形的面积÷边长=边长(不一定)
解决实际问题
图上距离/cm 1 2 3 4 5 6 7 ……
实际距离/m ……
这幅地图的比例尺是( )
解决实际问题
x 2
y 60 120
如果x和y成正比例,方框里应该填( );
如果x和y成反比例,方框里应该填( )。
4
1
解决实际问题
如果4a=3b, a和b成( )比例
正
a:b=3:4
反
ab=3×4
ab=12
回顾与延伸
在同一地点,同一时间,竹竿高度与影子的长度的比值是一定的,说明竹竿的高度与影子的长度成正比例。
一根垂直放置的高2米的竹竿在地上形成的影子长度是3米,同时附近一幢楼房影子的长度是米,这幢楼房高多少米?
竹竿高度:影子长度=楼房高度:影子长度
你有办法测量我们教学楼的高度吗?
回顾与延伸
把一个长方体铁块,熔铸成圆柱体,铁块的体积没有变。
底面积×高=铁块的体积(一定),底面积和高成反比例。
将一个底面积36平方分米,高6分米长方体钢材熔铸成高是10分米的圆柱体,这个圆柱底面积是多少平方分米?
长方体底面积×高=圆柱底面积×高
回顾与延伸
正比例
反比例
数量/本 1 3 6 8
总价/元 4 12 24 32
单价/元 2 3 4 5
数量/本 30 20 15 12
(1)购买同一种笔记本的数量和总价如下表。
(2)用同样的钱购买不同笔记本的单价和数量如下表。
判断下列各题中的两种量是什么比例关系,并说明理由。
数量/本 1 3 6 8
总价/元 4 12 24 32
单价/元 2 3 4 5
数量/本 30 20 15 12
(1)购买同一种笔记本的数量和总价如下表。
数量和总价成正比例。
总价÷数量=单价(一定)
(2)用同样的钱购买不同笔记本的单价和数量如下表。
单价和数量成反比例。
单价×数量=总价(一定)
数量/本 1 3 6 8
总价/元 4 12 24 32
单价/元 2 3 4 5
数量/本 30 20 15 12
(1)购买同一种笔记本的数量和总价如下表。
(2)用同样的钱购买不同笔记本的单价和数量如下表。
数量和总价成正比例。
单价和数量成反比例。
不同 相同
正比例
反比例
数量/本 1 3 6 8
总价/元 4 12 24 32
单价/元 2 3 4 5
数量/本 30 20 15 12
(1)购买同一种笔记本的数量和总价如下表。
(2)用同样的钱购买不同笔记本的单价和数量如下表。
如果购买笔记本的数量一定,
笔记本的单价和总价成( )比例。
正
数量/本 1 3 6 8
总价/元 4 12 24 32
单价/元 2 3 4 5
数量/本 30 20 15 12
(1)购买同一种笔记本的数量和总价如下表。
(2)用同样的钱购买不同笔记本的单价和数量如下表。
如果购买笔记本的数量一定,
笔记本的单价和总价成( )比例。
正
数量和单价成反比例
数量和总价成正比例
总价和单价成正比例
单价一定
总价一定
数量一定
数量和单价成反比例
数量和总价成正比例
总价和单价成正比例
单价一定
总价一定
数量一定
比值一定
乘积一定
你还能举出这样类似的例子吗?
快速判断
四名同学看《我们爱科学》这本书。
王新明 李虹 张志华 郑强
每天看的页数 20 15 10 6
需要看到天数 9 12 18 30
每天看的页数和需要的天数成反比例
快速判断
图上距离和实际距离成正比例
快速判断
跳绳的时间和总个数成正比例
每分钟跳绳的个数是一定的,
跳绳的时间和总个数。
总个数÷跳绳的时间=每分钟跳绳的个数(一定)
快速判断
地砖的面积和地砖的数量反比例
给一个房间的地面铺地砖,
地砖的面积和地砖的数量。
地砖的数量×地砖的面积=房间的面积(一定)
快速判断
人的身高和体重不成比例
人的身高和体重
快速判断
已经修的长度和还剩的长度不成比例
修一条公路,已经修的长度和还剩的长度。
已经修到长度+还剩的程度=公路全长(一定)
快速判断
圆的直径和周长正比例
圆的直径和周长
圆的周长÷直径=圆周率(一定)
快速判断
正方形边长和面积不成比例
正方形边长和面积
正方形的面积÷边长=边长(不一定)
解决实际问题
图上距离/cm 1 2 3 4 5 6 7 ……
实际距离/m ……
这幅地图的比例尺是( )
解决实际问题
x 2
y 60 120
如果x和y成正比例,方框里应该填( );
如果x和y成反比例,方框里应该填( )。
4
1
解决实际问题
如果4a=3b, a和b成( )比例
正
a:b=3:4
反
ab=3×4
ab=12
回顾与延伸
在同一地点,同一时间,竹竿高度与影子的长度的比值是一定的,说明竹竿的高度与影子的长度成正比例。
一根垂直放置的高2米的竹竿在地上形成的影子长度是3米,同时附近一幢楼房影子的长度是米,这幢楼房高多少米?
竹竿高度:影子长度=楼房高度:影子长度
你有办法测量我们教学楼的高度吗?
回顾与延伸
把一个长方体铁块,熔铸成圆柱体,铁块的体积没有变。
底面积×高=铁块的体积(一定),底面积和高成反比例。
将一个底面积36平方分米,高6分米长方体钢材熔铸成高是10分米的圆柱体,这个圆柱底面积是多少平方分米?
长方体底面积×高=圆柱底面积×高
回顾与延伸
正比例
反比例
