北师大版八年级数学上册 3.3 轴对称与坐标变化教案
文档属性
| 名称 | 北师大版八年级数学上册 3.3 轴对称与坐标变化教案 |
|
|
| 格式 | docx | ||
| 文件大小 | 117.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 13:39:56 | ||
图片预览

文档简介
第三章 位置与坐标
3. 轴对称与坐标变化
教学目标:
1、在同一直角坐标系中,感受图形上点的坐标变化与图形的轴对称变换之间的关系.
2、经历图形坐标变化与图形轴对称之间关系的探索过程,发展形象思维能力和数形结合意识。
教学重点:
经历图形坐标变化与图形轴对称之间关系的探索过程,明确图形坐标变化与图形轴对称之间关系。
教学难点:
由坐标的变化探索新旧图形之间的变化探索过程,发展形象思维能力和数形结合意识。
教学方法:引导发现法
教学过程:
第一环节 情景引入:
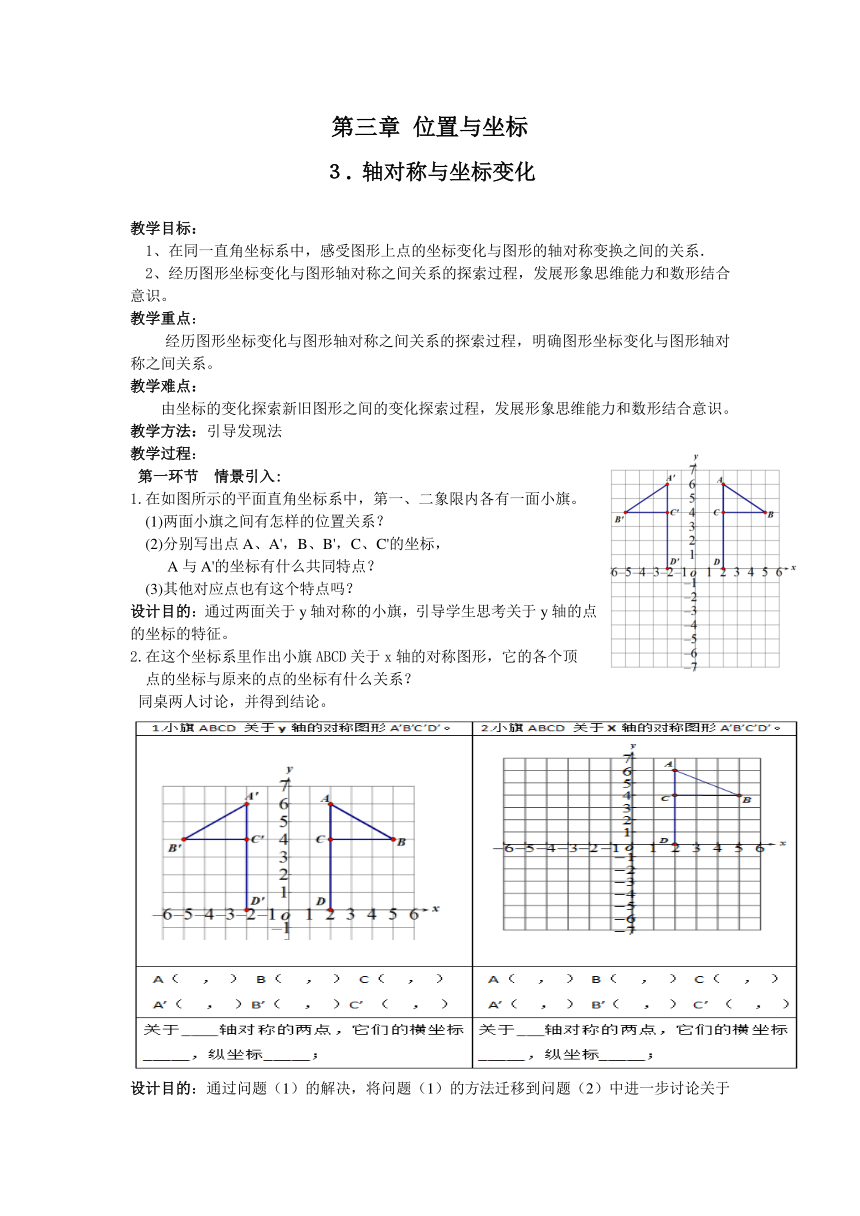
1.在如图所示的平面直角坐标系中,第一、二象限内各有一面小旗。
(1)两面小旗之间有怎样的位置关系?
(2)分别写出点A、A',B、B',C、C'的坐标,
A与A'的坐标有什么共同特点?
(3)其他对应点也有这个特点吗?
设计目的:通过两面关于y轴对称的小旗,引导学生思考关于y轴的点
的坐标的特征。
在这个坐标系里作出小旗ABCD关于x轴的对称图形,它的各个顶
点的坐标与原来的点的坐标有什么关系?
同桌两人讨论,并得到结论。
设计目的:通过问题(1)的解决,将问题(1)的方法迁移到问题(2)中进一步讨论关于x轴对称的点的坐标的特征,借助于两人小组活动进一步总结归纳两个关于坐标轴对称的图形的坐标关系,建立“数”与“形”之间的联系,发展学生的数形结合意识。
第二环节 探索新知:
1.在方格纸上建立直角坐标系,根据我读出的点的坐标在纸上找到相应的点,并依次用线段将这些点连接起来。坐标是(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)。
2.将上图中的点(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)做以下变化:
(1)纵坐标保持不变,横坐标分别乘以-1,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化?
横坐标保持不变,纵坐标分别乘以-1,再将所得的
点用线段依次连接起来,所得的图案与原来的图案相比
有什么变化?
设计目的:通过四人小组的形式探索以上三种情况,培养学生合作学习的能力,在合作学习及小组分享的过程进一步感受轴对称与坐标变化之间的关系。
第三环节 拓展练习:
点 A(2,- 3)关 于 x 轴 对 称 的 点 的 坐 标 是( B ).
A (-2,3) B( 2,3) C(2,-3) D(-2,-3)
2.点 B(-2,1)关 于 y 轴 对 称 的 点 的 坐 标 是( C ).
A (-2,-1) B( -2,1) C(2,1) D(2,-1)
3.点(4,3)与点(4,- 3)的关系是( B ) .
A.关于原点对称 B.关于 x轴对称 C.关于 y轴对称 D.不能构成对称关系
4.点(m,- 1)和点(2,n)关于 x轴对称,则 mn等于( A )
A.2 B.-2 C.1 D.- 1
5.已知点 P( a,b),Q(3,6),且 PQ ∥ x轴,则b的值为( C ) .
A.3 B.-6 C.6 D.- 3
6.已知点A(m+1,m-2)是x轴上一点,则点A关于y轴的对称点的坐标是( C )
A (-2,0) B( 0,-2) C(-3,0) D(0,-3)
7.在平面直角坐标系中,若点p(m,m-n)与点Q(-2,3)关于原点对称,则
点M(m,n)在 ( A )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8. 已知A、B两点的坐标分别是(-2,3)和(2,3),则下面四个结论:
①A、B关于x轴对称;②A、B关于y轴对称;
③A、B关于原点对称;④A、B之间的距离为4,其中正确的有( B )
A.1个 B.2个 C.3个 D.4个
9.点 A 在第一象限,当 m 为 B 时,点 A( m + 5,3m - 5)到 x轴的距离是
它到y轴距离的一半 .
A.5 B.3 C.-3 D.- 5
10.一束光线从点A(3,3)出发,经过y轴上点C反射后经过点B(1,0)则光线从A点到B点经过的路线长是( B )
A.4 B.5 C.6 D.7
第四环节 课堂小结:
1.今天你学到了哪些数学知识?
2.今天你学到了哪些数学方法?
数形结合法
第五环节 布置作业:
1、课堂作业: 课本69页 知识技能 1题
问题解决 2题
2、家庭作业; 学习之友
3. 轴对称与坐标变化
教学目标:
1、在同一直角坐标系中,感受图形上点的坐标变化与图形的轴对称变换之间的关系.
2、经历图形坐标变化与图形轴对称之间关系的探索过程,发展形象思维能力和数形结合意识。
教学重点:
经历图形坐标变化与图形轴对称之间关系的探索过程,明确图形坐标变化与图形轴对称之间关系。
教学难点:
由坐标的变化探索新旧图形之间的变化探索过程,发展形象思维能力和数形结合意识。
教学方法:引导发现法
教学过程:
第一环节 情景引入:
1.在如图所示的平面直角坐标系中,第一、二象限内各有一面小旗。
(1)两面小旗之间有怎样的位置关系?
(2)分别写出点A、A',B、B',C、C'的坐标,
A与A'的坐标有什么共同特点?
(3)其他对应点也有这个特点吗?
设计目的:通过两面关于y轴对称的小旗,引导学生思考关于y轴的点
的坐标的特征。
在这个坐标系里作出小旗ABCD关于x轴的对称图形,它的各个顶
点的坐标与原来的点的坐标有什么关系?
同桌两人讨论,并得到结论。
设计目的:通过问题(1)的解决,将问题(1)的方法迁移到问题(2)中进一步讨论关于x轴对称的点的坐标的特征,借助于两人小组活动进一步总结归纳两个关于坐标轴对称的图形的坐标关系,建立“数”与“形”之间的联系,发展学生的数形结合意识。
第二环节 探索新知:
1.在方格纸上建立直角坐标系,根据我读出的点的坐标在纸上找到相应的点,并依次用线段将这些点连接起来。坐标是(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)。
2.将上图中的点(0,0),(5,4),(3,0),(5,1),(5,-1),(3,0),(4,-2),(0,0)做以下变化:
(1)纵坐标保持不变,横坐标分别乘以-1,再将所得的点用线段依次连接起来,所得的图案与原来的图案相比有什么变化?
横坐标保持不变,纵坐标分别乘以-1,再将所得的
点用线段依次连接起来,所得的图案与原来的图案相比
有什么变化?
设计目的:通过四人小组的形式探索以上三种情况,培养学生合作学习的能力,在合作学习及小组分享的过程进一步感受轴对称与坐标变化之间的关系。
第三环节 拓展练习:
点 A(2,- 3)关 于 x 轴 对 称 的 点 的 坐 标 是( B ).
A (-2,3) B( 2,3) C(2,-3) D(-2,-3)
2.点 B(-2,1)关 于 y 轴 对 称 的 点 的 坐 标 是( C ).
A (-2,-1) B( -2,1) C(2,1) D(2,-1)
3.点(4,3)与点(4,- 3)的关系是( B ) .
A.关于原点对称 B.关于 x轴对称 C.关于 y轴对称 D.不能构成对称关系
4.点(m,- 1)和点(2,n)关于 x轴对称,则 mn等于( A )
A.2 B.-2 C.1 D.- 1
5.已知点 P( a,b),Q(3,6),且 PQ ∥ x轴,则b的值为( C ) .
A.3 B.-6 C.6 D.- 3
6.已知点A(m+1,m-2)是x轴上一点,则点A关于y轴的对称点的坐标是( C )
A (-2,0) B( 0,-2) C(-3,0) D(0,-3)
7.在平面直角坐标系中,若点p(m,m-n)与点Q(-2,3)关于原点对称,则
点M(m,n)在 ( A )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
8. 已知A、B两点的坐标分别是(-2,3)和(2,3),则下面四个结论:
①A、B关于x轴对称;②A、B关于y轴对称;
③A、B关于原点对称;④A、B之间的距离为4,其中正确的有( B )
A.1个 B.2个 C.3个 D.4个
9.点 A 在第一象限,当 m 为 B 时,点 A( m + 5,3m - 5)到 x轴的距离是
它到y轴距离的一半 .
A.5 B.3 C.-3 D.- 5
10.一束光线从点A(3,3)出发,经过y轴上点C反射后经过点B(1,0)则光线从A点到B点经过的路线长是( B )
A.4 B.5 C.6 D.7
第四环节 课堂小结:
1.今天你学到了哪些数学知识?
2.今天你学到了哪些数学方法?
数形结合法
第五环节 布置作业:
1、课堂作业: 课本69页 知识技能 1题
问题解决 2题
2、家庭作业; 学习之友
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
