2021-2022学年人教版七年级数学上册3.3.1解一元一次方程去括号 课件(共28张PPT)
文档属性
| 名称 | 2021-2022学年人教版七年级数学上册3.3.1解一元一次方程去括号 课件(共28张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 620.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 00:00:00 | ||
图片预览







文档简介
(共28张PPT)
空白演示
单击输入您的封面副标题
第三章 一元一次方程
3.3 解一元一次方程(二)
第1课时 利用去括号解一元一次方程
学 习 目 标
1
2
了解“去括号”是解方程的重要步骤.
熟练地运用去括号法则解带有括号的一元一次方程. (难点、重点)
1.化简下列各式:
(1) (-3a+2b) +3(a-b);
(2) -5+4-(-3+ ).
解: (1) 原式;
(2) 原式.
去括号法则
去掉“+ ( )”,括号内各项的符号不变. a + (b + c) =a + b + c.
去掉“– ( )”,括号内各项的符号改变. a -(b + c) =a -b - c.
温故知新
温故知新
2.解方程:
6x-7=4x-1
解:
移项得:
6x-4x=7-1
合并同类项得:
2x=6
系数化为1得:
x=3
移项,合并同类项,系数化为1,要注意些什么?
1.移项要变号;
2.合并同类项时系数相加,字母部分不变;
3.系数化为1时方程两边同时除以未知数的系数。
某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2000度,全年用电15万度,这个工厂去年上半年每月平均用电多少度?
分析:
设去年上半年每月平均用电x度.则下半年每月平均用电_______;
去年上半年用电合计为 度;
去年下半年用电合计为 度;
根据题意可列方程为________________________
6x
已知去年全年的用电合计为15万度
等式中含有括号,如何求得方程的解呢?
6(x-2000)
6x+6(x-2000)=150000
新课导入
(x-2000)
如何求方程6x+6(x-2000)=150000的解?
解:
去括号
移项
12x =162000
6x+6(x-2 000)=150 000
合并同类项
6x+6x-12000=150000
6x+6x =150000+12000
系数化为1
x=13500
提示:把它变成x=a(常数)的形式
去括号法则:
⑴括号前是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变符号。
简记:是“+”号,不变号。
⑵括号前是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变符号。
简记:是“-”号,全变号。
例1:
解下列方程
去括号
移项
-6x=8
(1)2x-(x+10)=5x+2(x-l):
合并同类项
2x-x-10=5x+2x-2
2x-x-5x-2x=-2+10
系数化为1
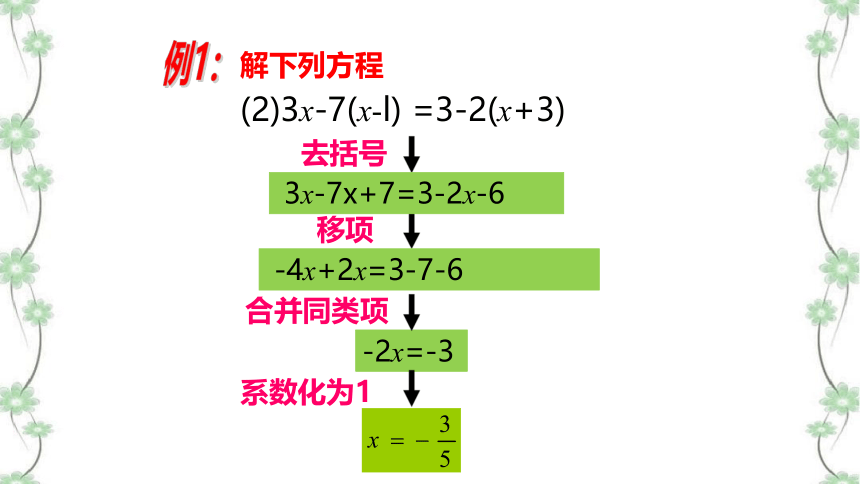
例1:
解下列方程
去括号
移项
-2x=-3
(2)3x-7(x-l) =3-2(x+3)
合并同类项
3x-7x+7=3-2x-6
-4x+2x=3-7-6
系数化为1
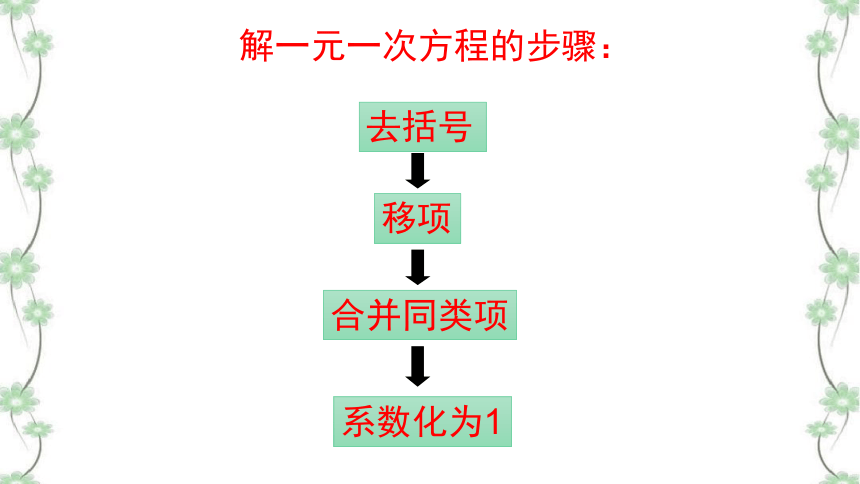
解一元一次方程的步骤:
移项
合并同类项
系数化为1
去括号
学以致用
1.下列变形对吗?若不对,请说明理由,并改正:
解方程
去括号,得
移项,得
合并同类项,得
两边同除以-0.2得
去括号变形错,有一项
没变号,改正如下:
去括号,得3-0.4x-2=0.2x
移项,得 -0.4x-0.2x=-3+2
合并同类项,得 -0.6x=-1
∴
注:方程中有带括号的式子时,去括号是常用的化简步骤.
2.解方程:(1)3(5x-1)- 2(3x+2)=6(x-1)+2
解:去括号,得
15x-3-6x-4 =6x-6+2
移项得
15x-6x-6x =-6+2+3+4
合并同类项得
3x =3
系数化为1,得
x =1
学以致用
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
学以致用
若方程2x+1=﹣3的解是关于x的方程7﹣2(x﹣a)=3的解,则a的值为( )
A.﹣2 B.﹣4 C.﹣5 D.﹣6
【提示】
解方程2x+1=﹣3,得到x的值并代入方程7﹣2(x﹣a)=3,得到关于a的一元一次方程,解之即可.
【详解】
解:解方程2x+1=﹣3化简得,x=﹣2,
把x=﹣2代入方程7﹣2(x﹣a)=3得,7﹣2(﹣2﹣a)=3,
解得:a=﹣4
学以致用
1.行程问题中的基本关系式是什么?
回忆:
路程=速度×时间
2.船在水中航行,它的速度都和哪些量有关,这些量之间的关系是怎样的?
顺水速度=静水速度+水流速度
逆水速度=静水速度-水流速度
3.题中等量关系是什么?
顺流速度×顺流时间=逆流速度×逆流时间
分析:等量关系:这艘船往返的路程相等,即
顺流速度___顺流时间___逆流速度___逆流时间
×
=
×
例2.一艘船从甲码头到乙码头顺流行驶,用了2 h;从乙码头返回甲码头逆流行驶,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的速度?
去括号解方程的应用
解:设船在静水中的平均速度为x km/h,则顺流的速度为(x+3) km/h,逆流速度为(x-3) km/h.
去括号,得
移项及合并同类项,得
系数化为1,得
答:船在静水中的平均速度为 27 km/h.
×
根据顺流速度___顺流时间___逆流速度 ___逆流时间
列出方程,得
×
=
一架飞机在两城之间航行,风速为24 km/h,顺风飞行要2小时50分,逆风飞行要3小时,求两城距离.
解:设飞机在无风时的速度为x km/h,则在顺风中的速度为(x+24) km/h ,在逆风中的速度为(x-24) km/h.
根据题意,得
解得
两城市的距离为
答:两城市之间的距离为2 448 km.
练一练
练一练
爷爷现在的年龄是孙子的5倍,12年后,爷爷的年龄是孙子的3倍,现在孙子的年龄是_____岁.
解得x=12.
解析:
设孙子的年龄为x岁,则爷爷的年龄为5x岁,
12年后,孙子的年龄为(x+12)岁,爷爷的年龄为 (5x+12)岁.
根据题意,得5x+12=3(x+12),
12
随堂训练
1.对于方程2(2x-1) - ( -3)=1,去括号正确的是( )
D
【解析】去括号时,当括号前面是“-”号,括
号内的各项都要改变符号,
2(2x-1) - ( -3)=1去括号得4x-2-x-3=1.
A.4x-1-x-3=1 B. 4x -1- x+3 =1
C.4x-2-x-3=1 D.4x-2-x+3=1
2.已知关于x的方程3x+2a=2的解是x=a-1,则a 的值为( )
A. 1 B. C. D.-1
A
【解析】把x=a-1代入原方程,得3(a-1)+2a=2,解得a=1。
3.若关于x的方程 3x + ( 2a+1 ) = x-( 3a+2 ) 的解为x = 0,
则a的值等于 ( )
A. B. C. D.
D
4.当x= 时,代数式2(x2-1)-x2的值比代数式 x2+3x-2的值大6.
-2
解下列方程 .
(1)3x-5(x-3)=9-(x+4)
(2) 6y =-2(3y-5) +14
解:去括号,得
合并同类项,得
系数化成1,得
经检验:x =10是原方程的解。
移项,得
合并同类项,得
系数化成1,得
经检验:y =2是原方程的解。
3x-5x+15 = 9- x - 4
移项,得
3x-5x+ x = 9- 4- 15
-x = - 10
x = 10
解:去括号,得
6y =-6y + 10 +14
6y + 6y = 10 +14
12y = 24
y = 2
5.解下列方程 .
(3)-2(z+5)=3(z-5)-5
解:去括号,得
合并同类项,得
系数化成1,得
经检验:z=2是原方程的解。
移项,得
合并同类项,得
系数化成1,得
经检验:m =10是原方程的解。
移项,得
解:去括号,得
-2z - 10 =3z-15-6
-2x - 3x =-15-5 +10
-5z =-10
z = 2
6.毕业在即,九年级某班为纪念师生情谊,班委决定花800元班费买两种不同单价的留念册,分别给50位同学和10位任课老师每人一本留做纪念,其中送给任课老师的留念册的单价比给同学的单价多8元,请问这两种不同留念册的单价分别为多少元?
解:设送给任课老师的留念册的单价为x元,
10x+50( x-8)=800
解得x=20, x-8=12
答:送给任课老师的留念册的单价为20元,送给同学的留念册的单价为12元.
丢番图的墓志铭
墓中长眠着一个伟大的人物——丢番图
他的一生的六分之一时光,是童年时代; 又度过了十二分之一岁月后, 他满脸长出了胡须;再过了七分之一年月时, 举行了花烛盛典;婚后五年, 得一贵子。可是不幸的孩子,他仅仅活了父亲的半生时光,就离开了人间。 从此,作为父亲的丢番图,在悲伤中度过了四年后, 结束了自己的一生。
阅读材料
你能算出丢番图生活的岁数吗?
可设他生活的岁数 为x,则:
上帝给予的童年占六分之一
又过十二分之一,两颊长胡
再过七分之一,点燃起结婚的蜡烛
五年之后天赐贵子
可怜迟到的宁馨儿,享年仅其父之半,
便进入冰冷的墓
又过四年,他也走完了人生的旅途
请你算一算,丢番图一共活了多少年?
2.为鼓励居民节约用电,某地对居民用户用电收费标准作如下规定:每户每月用电如果不超过100度,那么每度按0.50元收费;如果超过100度不超过200度,那么超过部分每度按0.65元收费;如果超过200度,那么超过部分每度按0.75元收费.若某户居民在9月份缴纳电费310元,那么他这个月用电多少度?
解:设他这个月用电x度,根据题意,得
提示:若一个月用电200度,则这个月应缴纳电费为0.50×100+0.65×
=115(元).故当缴纳电费为310元时,该用户9月份用电量超过200度.
解得.
答:他这个月用电460度.
空白演示
单击输入您的封面副标题
第三章 一元一次方程
3.3 解一元一次方程(二)
第1课时 利用去括号解一元一次方程
学 习 目 标
1
2
了解“去括号”是解方程的重要步骤.
熟练地运用去括号法则解带有括号的一元一次方程. (难点、重点)
1.化简下列各式:
(1) (-3a+2b) +3(a-b);
(2) -5+4-(-3+ ).
解: (1) 原式;
(2) 原式.
去括号法则
去掉“+ ( )”,括号内各项的符号不变. a + (b + c) =a + b + c.
去掉“– ( )”,括号内各项的符号改变. a -(b + c) =a -b - c.
温故知新
温故知新
2.解方程:
6x-7=4x-1
解:
移项得:
6x-4x=7-1
合并同类项得:
2x=6
系数化为1得:
x=3
移项,合并同类项,系数化为1,要注意些什么?
1.移项要变号;
2.合并同类项时系数相加,字母部分不变;
3.系数化为1时方程两边同时除以未知数的系数。
某工厂加强节能措施,去年下半年与上半年相比,月平均用电量减少2000度,全年用电15万度,这个工厂去年上半年每月平均用电多少度?
分析:
设去年上半年每月平均用电x度.则下半年每月平均用电_______;
去年上半年用电合计为 度;
去年下半年用电合计为 度;
根据题意可列方程为________________________
6x
已知去年全年的用电合计为15万度
等式中含有括号,如何求得方程的解呢?
6(x-2000)
6x+6(x-2000)=150000
新课导入
(x-2000)
如何求方程6x+6(x-2000)=150000的解?
解:
去括号
移项
12x =162000
6x+6(x-2 000)=150 000
合并同类项
6x+6x-12000=150000
6x+6x =150000+12000
系数化为1
x=13500
提示:把它变成x=a(常数)的形式
去括号法则:
⑴括号前是“+”号,把括号和它前面的“+”号去掉,括号里各项都不变符号。
简记:是“+”号,不变号。
⑵括号前是“-”号,把括号和它前面的“-”号去掉,括号里各项都改变符号。
简记:是“-”号,全变号。
例1:
解下列方程
去括号
移项
-6x=8
(1)2x-(x+10)=5x+2(x-l):
合并同类项
2x-x-10=5x+2x-2
2x-x-5x-2x=-2+10
系数化为1
例1:
解下列方程
去括号
移项
-2x=-3
(2)3x-7(x-l) =3-2(x+3)
合并同类项
3x-7x+7=3-2x-6
-4x+2x=3-7-6
系数化为1
解一元一次方程的步骤:
移项
合并同类项
系数化为1
去括号
学以致用
1.下列变形对吗?若不对,请说明理由,并改正:
解方程
去括号,得
移项,得
合并同类项,得
两边同除以-0.2得
去括号变形错,有一项
没变号,改正如下:
去括号,得3-0.4x-2=0.2x
移项,得 -0.4x-0.2x=-3+2
合并同类项,得 -0.6x=-1
∴
注:方程中有带括号的式子时,去括号是常用的化简步骤.
2.解方程:(1)3(5x-1)- 2(3x+2)=6(x-1)+2
解:去括号,得
15x-3-6x-4 =6x-6+2
移项得
15x-6x-6x =-6+2+3+4
合并同类项得
3x =3
系数化为1,得
x =1
学以致用
解:去括号,得
移项,得
合并同类项,得
系数化为1,得
学以致用
若方程2x+1=﹣3的解是关于x的方程7﹣2(x﹣a)=3的解,则a的值为( )
A.﹣2 B.﹣4 C.﹣5 D.﹣6
【提示】
解方程2x+1=﹣3,得到x的值并代入方程7﹣2(x﹣a)=3,得到关于a的一元一次方程,解之即可.
【详解】
解:解方程2x+1=﹣3化简得,x=﹣2,
把x=﹣2代入方程7﹣2(x﹣a)=3得,7﹣2(﹣2﹣a)=3,
解得:a=﹣4
学以致用
1.行程问题中的基本关系式是什么?
回忆:
路程=速度×时间
2.船在水中航行,它的速度都和哪些量有关,这些量之间的关系是怎样的?
顺水速度=静水速度+水流速度
逆水速度=静水速度-水流速度
3.题中等量关系是什么?
顺流速度×顺流时间=逆流速度×逆流时间
分析:等量关系:这艘船往返的路程相等,即
顺流速度___顺流时间___逆流速度___逆流时间
×
=
×
例2.一艘船从甲码头到乙码头顺流行驶,用了2 h;从乙码头返回甲码头逆流行驶,用了2.5 h.已知水流的速度是3 km/h,求船在静水中的速度?
去括号解方程的应用
解:设船在静水中的平均速度为x km/h,则顺流的速度为(x+3) km/h,逆流速度为(x-3) km/h.
去括号,得
移项及合并同类项,得
系数化为1,得
答:船在静水中的平均速度为 27 km/h.
×
根据顺流速度___顺流时间___逆流速度 ___逆流时间
列出方程,得
×
=
一架飞机在两城之间航行,风速为24 km/h,顺风飞行要2小时50分,逆风飞行要3小时,求两城距离.
解:设飞机在无风时的速度为x km/h,则在顺风中的速度为(x+24) km/h ,在逆风中的速度为(x-24) km/h.
根据题意,得
解得
两城市的距离为
答:两城市之间的距离为2 448 km.
练一练
练一练
爷爷现在的年龄是孙子的5倍,12年后,爷爷的年龄是孙子的3倍,现在孙子的年龄是_____岁.
解得x=12.
解析:
设孙子的年龄为x岁,则爷爷的年龄为5x岁,
12年后,孙子的年龄为(x+12)岁,爷爷的年龄为 (5x+12)岁.
根据题意,得5x+12=3(x+12),
12
随堂训练
1.对于方程2(2x-1) - ( -3)=1,去括号正确的是( )
D
【解析】去括号时,当括号前面是“-”号,括
号内的各项都要改变符号,
2(2x-1) - ( -3)=1去括号得4x-2-x-3=1.
A.4x-1-x-3=1 B. 4x -1- x+3 =1
C.4x-2-x-3=1 D.4x-2-x+3=1
2.已知关于x的方程3x+2a=2的解是x=a-1,则a 的值为( )
A. 1 B. C. D.-1
A
【解析】把x=a-1代入原方程,得3(a-1)+2a=2,解得a=1。
3.若关于x的方程 3x + ( 2a+1 ) = x-( 3a+2 ) 的解为x = 0,
则a的值等于 ( )
A. B. C. D.
D
4.当x= 时,代数式2(x2-1)-x2的值比代数式 x2+3x-2的值大6.
-2
解下列方程 .
(1)3x-5(x-3)=9-(x+4)
(2) 6y =-2(3y-5) +14
解:去括号,得
合并同类项,得
系数化成1,得
经检验:x =10是原方程的解。
移项,得
合并同类项,得
系数化成1,得
经检验:y =2是原方程的解。
3x-5x+15 = 9- x - 4
移项,得
3x-5x+ x = 9- 4- 15
-x = - 10
x = 10
解:去括号,得
6y =-6y + 10 +14
6y + 6y = 10 +14
12y = 24
y = 2
5.解下列方程 .
(3)-2(z+5)=3(z-5)-5
解:去括号,得
合并同类项,得
系数化成1,得
经检验:z=2是原方程的解。
移项,得
合并同类项,得
系数化成1,得
经检验:m =10是原方程的解。
移项,得
解:去括号,得
-2z - 10 =3z-15-6
-2x - 3x =-15-5 +10
-5z =-10
z = 2
6.毕业在即,九年级某班为纪念师生情谊,班委决定花800元班费买两种不同单价的留念册,分别给50位同学和10位任课老师每人一本留做纪念,其中送给任课老师的留念册的单价比给同学的单价多8元,请问这两种不同留念册的单价分别为多少元?
解:设送给任课老师的留念册的单价为x元,
10x+50( x-8)=800
解得x=20, x-8=12
答:送给任课老师的留念册的单价为20元,送给同学的留念册的单价为12元.
丢番图的墓志铭
墓中长眠着一个伟大的人物——丢番图
他的一生的六分之一时光,是童年时代; 又度过了十二分之一岁月后, 他满脸长出了胡须;再过了七分之一年月时, 举行了花烛盛典;婚后五年, 得一贵子。可是不幸的孩子,他仅仅活了父亲的半生时光,就离开了人间。 从此,作为父亲的丢番图,在悲伤中度过了四年后, 结束了自己的一生。
阅读材料
你能算出丢番图生活的岁数吗?
可设他生活的岁数 为x,则:
上帝给予的童年占六分之一
又过十二分之一,两颊长胡
再过七分之一,点燃起结婚的蜡烛
五年之后天赐贵子
可怜迟到的宁馨儿,享年仅其父之半,
便进入冰冷的墓
又过四年,他也走完了人生的旅途
请你算一算,丢番图一共活了多少年?
2.为鼓励居民节约用电,某地对居民用户用电收费标准作如下规定:每户每月用电如果不超过100度,那么每度按0.50元收费;如果超过100度不超过200度,那么超过部分每度按0.65元收费;如果超过200度,那么超过部分每度按0.75元收费.若某户居民在9月份缴纳电费310元,那么他这个月用电多少度?
解:设他这个月用电x度,根据题意,得
提示:若一个月用电200度,则这个月应缴纳电费为0.50×100+0.65×
=115(元).故当缴纳电费为310元时,该用户9月份用电量超过200度.
解得.
答:他这个月用电460度.
