北师大版八年级数学上册 第四章 一次函数 复习课件(共23张PPT)
文档属性
| 名称 | 北师大版八年级数学上册 第四章 一次函数 复习课件(共23张PPT) |

|
|
| 格式 | pptx | ||
| 文件大小 | 614.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 00:00:00 | ||
图片预览







文档简介
(共23张PPT)
第四章 一次函数 复习课件
1、理解一次函数、正比例函数的概念;
2、理解一次函数、正比例函数的性质;
3、会画一次函数、正比例函数的图像;
4、会用待定系数法求一次函数关系式。
5、利用一次函数及其图象,会解决实际问题。
复习目标
问题:同学们回忆一下我们是从哪些方面着手研究一次函数的呢?
定义
图象
性质
应用
1、一次函数定义
函数形如__________________________叫做一次函数。
当_____时,______________是正比例函数。
正比例函数与一次函数的联系是什么?
正比例函数是特殊的一次函数。
y=kx+b(k、b为常数,k≠0)
b=0
y=kx(k≠0)
一、知识回顾,熟悉考点
1、一次函数定义
m_____时,函数 是一次函数。
=1
判断是一次函数的条件是什么?
1、自变量的指数=1。
2、自变量前的系数k≠0。
若y=(m-2)x+m2-4是关于x的正比例函数,则m_________。
=-2
1、一次函数定义
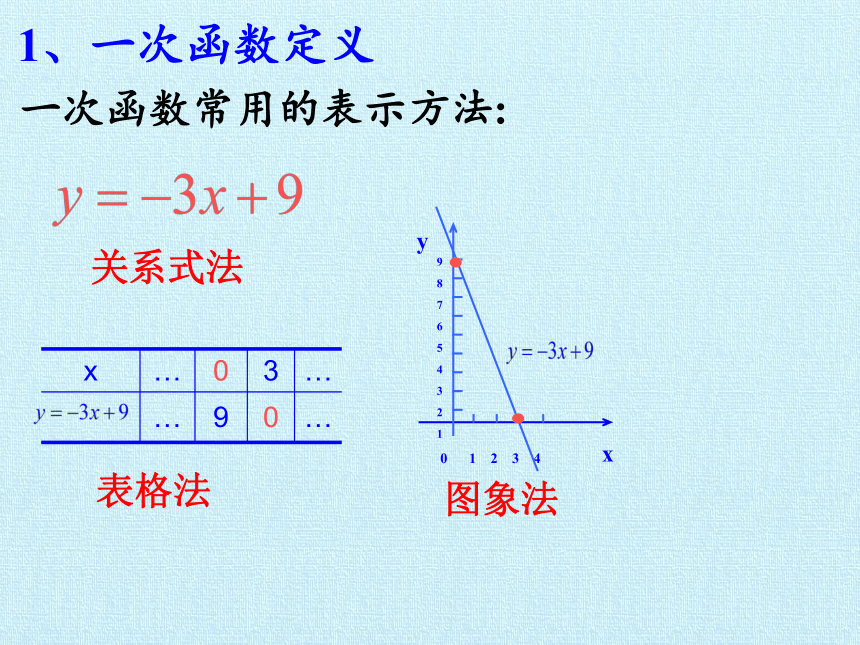
图象法
表格法
关系式法
一次函数常用的表示方法:
1、一次函数定义
y
x
9
8
7
6
5
4
3
2
1
0 1 2 3 4
x … 0 3 …
… 9 0 …
2、一次函数图象及性质
1.作函数图象有几个步骤?
2.正比例函数y=kx和一次函数y=kx+b图象有什么特点?
3.作正比例函数和一次函数图象需要描出几个点?
列表
描点
连线
一次函数的图象是____________________的一条直线。
只需要描出两个点。(两点法)
(1,k)
(0,0)
(0,b)
,0)
(
正比例函数的图象是__________________的一条直线。
过原点(0,0)
过(0,b)
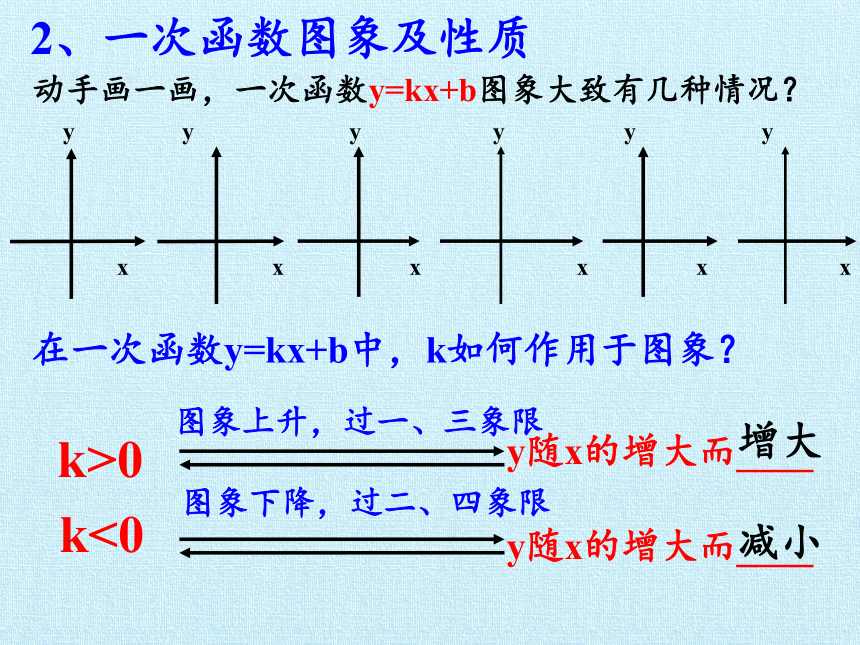
动手画一画,一次函数y=kx+b图象大致有几种情况?
2、一次函数图象及性质
x x x x x x
y y y y y y
k>0
y随x的增大而____
k<0
y随x的增大而____
图象上升,过一、三象限
图象下降,过二、四象限
在一次函数y=kx+b中,k如何作用于图象?
减小
增大
x x x x x x
y y y y y y
在一次函数y=kx+b中,b如何作用于图象?
b决定直线与y轴交点的位置
b>0
b<0
直线与y轴交于正半轴
直线与y轴交于负半轴
b=0
直线必过原点(0,0)
2、一次函数图象及性质
1.根据下列一次函数y=kx+b(k≠0)的草图回答出各图中k、b的符号:
o
y
x
o
y
x
K<0,b>0
k>0,b<0
2、一次函数图象及性质
2.一次函数y=3x-4的图像不经过的象限( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
∣k∣决定直线的倾斜度
当∣k∣越大时,直线______,函数值变化________。
当∣k∣越小时,直线______,函数值变化________。
越陡
越缓
越快
越慢
y
-4
-2
-3
-1
2
1
0
-2
-3
1
2
3
4
x
-1
3
y=x
y=3x
y=-x
y=-4x
如图所示,下列结论中正确的是( )
A. B.
C. D.
A
(1)点(-1,5)在这个函数图象上吗?
(2)这个函数图象分别与x轴,y轴的交点坐标是什么?在这个函数图象上,y随x的增大怎么样变化?
(3)已知点P(x1,y1),Q(x2,y2)在这个函数图象上,且x1自主探究,预习反馈
请作出一次函数y=-2x+4的图象,回答以下几个问题:
比较函数值大小的方法:
特值法
性质法
图象法
(4)此函数图象与函数y=-2x的图象有什么位置关系?
此函数图象与函数y=x的图象又有什么位置关系?
将直线y=-2x+4向下平移5个单位得到的函数关系式是什么?
请作出一次函数y=-2x+4的图象,回答以下几个问题:
一次函数图象上下平移是由b值变化引起的。
两直线的位置关系:
平行
k值相等,b值不等
相交
k值不等
一次函数图象平移规律:
(5)该函数与两坐标轴围成三角形面积和周长各是多少?
请作出一次函数y=-2x+4的图象,回答以下几个问题:
(1)一次函数与几何图形结合
点坐标
线段长度
3、一次函数图象的应用
请作出一次函数y=-2x+4的图象,回答以下几个问题:
(6)此函数与x轴的交点坐标与方程-2x+4=0的解有什么关系?此函数图象与函数y=2x图象的交点坐标是什么?
(2)一次函数与方程(组)的关系
3、一次函数图象的应用
一元一次方程kx+b=0的解是一次函数y=kx+b的图象与x轴交点的横坐标。
两个一次函数图象的交点坐标是对应的二元一次方程组的解。
一次函数的图象经过点(0,4)和点(1,2)。写出一次函数的表达式。
解:设一次函数的表达式为y=kx+b,
把(0,4)(1,2)分别代入关系式,得
4=b
2=k 1+b
∴ k= -2
b=4
∴该一次函数的表达式为y=-2x+4。
待定系数法
设、列、解、代
步骤
3、一次函数的应用
(3)确定一次函数表达式
二、小组合作,知识梳理
同学们通过小组交流合作,对自己本章整理的知识树,进行补充修改再整理,小组成员可以互相补充,每一组选出整理的最好的一份展示。
三、归纳与反思
通过本节课对一次函数相关知识的的复习,请你谈谈有哪些收获?
学好函数的关键是函数图像。
我们要学会从函数图像中分析、获取有用的信息,来帮助我们解题。
温馨提示:
在理解概念的基础上,
依托图形理解性质,
进一步注重应用。
一次函数y=-x+4的图象与x轴交于点A,与y轴交于点B,在x轴上是否存在点M,使△ABM为等腰三角形?若存在,把符合条件的点M的坐标都求出来;若不存在,请说明理由。
四、思维拓展,能力提升
谢 谢
第四章 一次函数 复习课件
1、理解一次函数、正比例函数的概念;
2、理解一次函数、正比例函数的性质;
3、会画一次函数、正比例函数的图像;
4、会用待定系数法求一次函数关系式。
5、利用一次函数及其图象,会解决实际问题。
复习目标
问题:同学们回忆一下我们是从哪些方面着手研究一次函数的呢?
定义
图象
性质
应用
1、一次函数定义
函数形如__________________________叫做一次函数。
当_____时,______________是正比例函数。
正比例函数与一次函数的联系是什么?
正比例函数是特殊的一次函数。
y=kx+b(k、b为常数,k≠0)
b=0
y=kx(k≠0)
一、知识回顾,熟悉考点
1、一次函数定义
m_____时,函数 是一次函数。
=1
判断是一次函数的条件是什么?
1、自变量的指数=1。
2、自变量前的系数k≠0。
若y=(m-2)x+m2-4是关于x的正比例函数,则m_________。
=-2
1、一次函数定义
图象法
表格法
关系式法
一次函数常用的表示方法:
1、一次函数定义
y
x
9
8
7
6
5
4
3
2
1
0 1 2 3 4
x … 0 3 …
… 9 0 …
2、一次函数图象及性质
1.作函数图象有几个步骤?
2.正比例函数y=kx和一次函数y=kx+b图象有什么特点?
3.作正比例函数和一次函数图象需要描出几个点?
列表
描点
连线
一次函数的图象是____________________的一条直线。
只需要描出两个点。(两点法)
(1,k)
(0,0)
(0,b)
,0)
(
正比例函数的图象是__________________的一条直线。
过原点(0,0)
过(0,b)
动手画一画,一次函数y=kx+b图象大致有几种情况?
2、一次函数图象及性质
x x x x x x
y y y y y y
k>0
y随x的增大而____
k<0
y随x的增大而____
图象上升,过一、三象限
图象下降,过二、四象限
在一次函数y=kx+b中,k如何作用于图象?
减小
增大
x x x x x x
y y y y y y
在一次函数y=kx+b中,b如何作用于图象?
b决定直线与y轴交点的位置
b>0
b<0
直线与y轴交于正半轴
直线与y轴交于负半轴
b=0
直线必过原点(0,0)
2、一次函数图象及性质
1.根据下列一次函数y=kx+b(k≠0)的草图回答出各图中k、b的符号:
o
y
x
o
y
x
K<0,b>0
k>0,b<0
2、一次函数图象及性质
2.一次函数y=3x-4的图像不经过的象限( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
B
∣k∣决定直线的倾斜度
当∣k∣越大时,直线______,函数值变化________。
当∣k∣越小时,直线______,函数值变化________。
越陡
越缓
越快
越慢
y
-4
-2
-3
-1
2
1
0
-2
-3
1
2
3
4
x
-1
3
y=x
y=3x
y=-x
y=-4x
如图所示,下列结论中正确的是( )
A. B.
C. D.
A
(1)点(-1,5)在这个函数图象上吗?
(2)这个函数图象分别与x轴,y轴的交点坐标是什么?在这个函数图象上,y随x的增大怎么样变化?
(3)已知点P(x1,y1),Q(x2,y2)在这个函数图象上,且x1
请作出一次函数y=-2x+4的图象,回答以下几个问题:
比较函数值大小的方法:
特值法
性质法
图象法
(4)此函数图象与函数y=-2x的图象有什么位置关系?
此函数图象与函数y=x的图象又有什么位置关系?
将直线y=-2x+4向下平移5个单位得到的函数关系式是什么?
请作出一次函数y=-2x+4的图象,回答以下几个问题:
一次函数图象上下平移是由b值变化引起的。
两直线的位置关系:
平行
k值相等,b值不等
相交
k值不等
一次函数图象平移规律:
(5)该函数与两坐标轴围成三角形面积和周长各是多少?
请作出一次函数y=-2x+4的图象,回答以下几个问题:
(1)一次函数与几何图形结合
点坐标
线段长度
3、一次函数图象的应用
请作出一次函数y=-2x+4的图象,回答以下几个问题:
(6)此函数与x轴的交点坐标与方程-2x+4=0的解有什么关系?此函数图象与函数y=2x图象的交点坐标是什么?
(2)一次函数与方程(组)的关系
3、一次函数图象的应用
一元一次方程kx+b=0的解是一次函数y=kx+b的图象与x轴交点的横坐标。
两个一次函数图象的交点坐标是对应的二元一次方程组的解。
一次函数的图象经过点(0,4)和点(1,2)。写出一次函数的表达式。
解:设一次函数的表达式为y=kx+b,
把(0,4)(1,2)分别代入关系式,得
4=b
2=k 1+b
∴ k= -2
b=4
∴该一次函数的表达式为y=-2x+4。
待定系数法
设、列、解、代
步骤
3、一次函数的应用
(3)确定一次函数表达式
二、小组合作,知识梳理
同学们通过小组交流合作,对自己本章整理的知识树,进行补充修改再整理,小组成员可以互相补充,每一组选出整理的最好的一份展示。
三、归纳与反思
通过本节课对一次函数相关知识的的复习,请你谈谈有哪些收获?
学好函数的关键是函数图像。
我们要学会从函数图像中分析、获取有用的信息,来帮助我们解题。
温馨提示:
在理解概念的基础上,
依托图形理解性质,
进一步注重应用。
一次函数y=-x+4的图象与x轴交于点A,与y轴交于点B,在x轴上是否存在点M,使△ABM为等腰三角形?若存在,把符合条件的点M的坐标都求出来;若不存在,请说明理由。
四、思维拓展,能力提升
谢 谢
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
