北师大版八年级数学上册 5.4 增收节支课件(共23张PPT)
文档属性
| 名称 | 北师大版八年级数学上册 5.4 增收节支课件(共23张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 803.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 15:42:42 | ||
图片预览








文档简介
(共23张PPT)
7.4 增收节支
1、某人去年每个月的工资是6000元,今年比去年增长了10%,则今年的工资为 元。
如果要扣除5%的税,则还剩
元。
6600
6270
问1:增长率公式
原来的量× =后来的量
(1+增长率)
问2:银行利率问题中的公式
(利息、本金、利率)
利息=本金×利率×期数(几年期)
本息和=本金+利息
2、某人按定期一年存入银行10000元,若年利率为2.25%,则一年后可得利息_______元;本息和为_________元
(不考虑利息税).
225
10225
3、某商品进价为2000元,卖出后可获利50%,则利润为 元,该商品的售价为 元。
1000
3000
问3:利润、利润率公式
进价× =利润
利润率
售价— =利润
进价
Mike一家的经济生活
购物问题
储蓄问题
收支问题
:
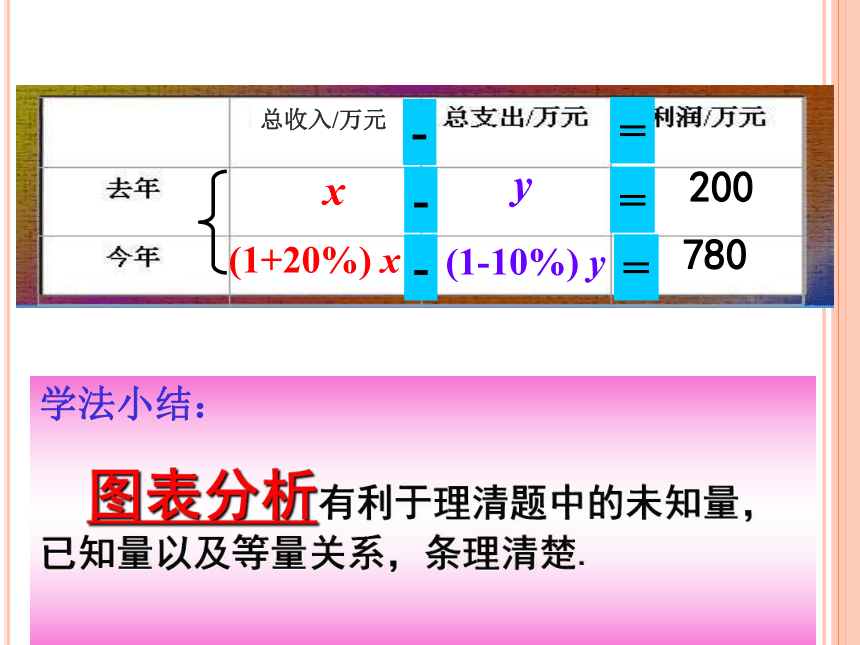
Mike的爸爸开了一家工厂,去年的利润(即总收入-总支出)为200万元。今年采取了一些增收节支的措施,结果,总收入比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元。问:去年的总收入、总支出各是多少万元?
一、收支问题
总收入
找一找:题目中出现了哪些量?
去年
今年
总支出
利润
Mike的爸爸开了一家工厂,去年的利润(即总收入-总支出)为200万元。今年采取了一些增收节支的措施,结果,总收入比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元。问:去年的总收入、总支出各是多少万元?
一、收支问题
总收入/万元
(1+20%) x
(1-10%) y
x
y
200
780
-
=
-
=
-
=
学法小结:
图表分析有利于理清题中的未知量,已知量以及等量关系,条理清楚.
总收入/万元
(1+20%) x
(1-10%) y
x
y
200
780
-
=
-
=
-
=
解:
设去年的总产值为x万元,总支出为y万元,由题意得
x - y=200
(1+20%)x-(1-10%)y=780
整理得:
x - y=200
4x - 3y=2600
解得:
x =2000
y=1800
答:去年的总产值为2000万元,
总支出为1800万元
Mike一家的经济生活
购物问题
储蓄问题
收支问题
:
Mike的妈妈喜欢存钱,最近她刚将8000元分成两部分存到银行:已知甲种储蓄的年利率为1.0%,乙种储蓄的年利率为1.1%.如果一年到期后,她可得利息85.5元(不扣利息税),问甲乙两种储蓄她各存了多少钱
二、储蓄问题
甲种储蓄 乙种储蓄 和
本金 x y
利息
甲种储蓄存了x元,乙种储蓄存了y元
8000
85.5
1.1%y
1.0%x
Mike一家的经济生活
购物问题
储蓄问题
收支问题
:
在新玛特、百货大楼同款的mp3的单价相同,书包单价也相同,mp3和书包单价之和是452元,且mp3的单价比书包单价的4倍少8元,你能算出mp3和书包单价各是多少元吗?
解:设书包单价为x元,mp3单价为y元,由题意得:
解得:
答:书包单价92元,随身听单价360元。
三、购物问题
1、育才学校去年有学生3100名,今年比去年增加4.4%,其中寄宿学生增加了6%,走读学生减少了2%.问该校去年有寄宿学生与走读学生各多少名 设去年有寄宿学生x名,走读学生y名,列出方程组
寄宿学生 走读学生 学生总数
去年
今年
x
y
3100
(1+6%)x
(1-2%)y
3100 ×
(1+4.4%)
2、一、二两班共有100名学生,他们的体育达标率(达到标准的百分率)为81%。如果一班学生的体育达标率为87.5%,二班的达标率为75%,那么一、二两班的学生数各是多少 设一班学生有x名、二班学生有y名,列出方程组
一班 二班 两班总和
学生数
达标学生数
x
87.5%x
y
75%y
100
81%×100
3、某公司用30000元购进甲乙两种货物.货物卖出后,甲种货物获利10%,乙种货物获利11%,共得利润3150元,问两种货物各进多少钱的货 设甲种货物进x元的货,乙种货物进 y元的货.列出方程组
甲种 乙种 总和
进货钱 X y
获利
30000
10%X
11%y
3150
4、用含糖分别为35%和40%的两种糖水混合,配制成含糖36%的糖水50千克,每种糖水应各取多少千克 设应取35%的糖水x千克,40%的糖水Y千克.列出方程组。
35%的糖水 40%的糖水 总和
糖水重量 X Y
含糖量
50
35%X
40%Y
50×36%
5、甲、乙两人从相距36千米的两地相向而行,如甲比乙先走2时,那么他们在乙出发2.5时后相遇;如果乙比甲先走2时,那么他们在甲出发3时后相遇,甲、乙两人每时各走多少千米 设甲、乙两人每时分别行走x千米,y千米。列出方程组
甲走的路程 乙走的路程
甲乙行走的路程和
甲先2小时
乙先2小时
(2+2.5)x
2.5y
36
36
3x
(2+3)y
做课本 P233 习题 2、3
列方程解应用题步骤
1·审题 (找等量关系)2·设未知数 3·列方程 4·解方程 5·检验·作答
关键:找等量关系. 列方程
做课本 P228习题 1(1、2)
7.4 增收节支
1、某人去年每个月的工资是6000元,今年比去年增长了10%,则今年的工资为 元。
如果要扣除5%的税,则还剩
元。
6600
6270
问1:增长率公式
原来的量× =后来的量
(1+增长率)
问2:银行利率问题中的公式
(利息、本金、利率)
利息=本金×利率×期数(几年期)
本息和=本金+利息
2、某人按定期一年存入银行10000元,若年利率为2.25%,则一年后可得利息_______元;本息和为_________元
(不考虑利息税).
225
10225
3、某商品进价为2000元,卖出后可获利50%,则利润为 元,该商品的售价为 元。
1000
3000
问3:利润、利润率公式
进价× =利润
利润率
售价— =利润
进价
Mike一家的经济生活
购物问题
储蓄问题
收支问题
:
Mike的爸爸开了一家工厂,去年的利润(即总收入-总支出)为200万元。今年采取了一些增收节支的措施,结果,总收入比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元。问:去年的总收入、总支出各是多少万元?
一、收支问题
总收入
找一找:题目中出现了哪些量?
去年
今年
总支出
利润
Mike的爸爸开了一家工厂,去年的利润(即总收入-总支出)为200万元。今年采取了一些增收节支的措施,结果,总收入比去年增加了20%,总支出比去年减少了10%,今年的利润为780万元。问:去年的总收入、总支出各是多少万元?
一、收支问题
总收入/万元
(1+20%) x
(1-10%) y
x
y
200
780
-
=
-
=
-
=
学法小结:
图表分析有利于理清题中的未知量,已知量以及等量关系,条理清楚.
总收入/万元
(1+20%) x
(1-10%) y
x
y
200
780
-
=
-
=
-
=
解:
设去年的总产值为x万元,总支出为y万元,由题意得
x - y=200
(1+20%)x-(1-10%)y=780
整理得:
x - y=200
4x - 3y=2600
解得:
x =2000
y=1800
答:去年的总产值为2000万元,
总支出为1800万元
Mike一家的经济生活
购物问题
储蓄问题
收支问题
:
Mike的妈妈喜欢存钱,最近她刚将8000元分成两部分存到银行:已知甲种储蓄的年利率为1.0%,乙种储蓄的年利率为1.1%.如果一年到期后,她可得利息85.5元(不扣利息税),问甲乙两种储蓄她各存了多少钱
二、储蓄问题
甲种储蓄 乙种储蓄 和
本金 x y
利息
甲种储蓄存了x元,乙种储蓄存了y元
8000
85.5
1.1%y
1.0%x
Mike一家的经济生活
购物问题
储蓄问题
收支问题
:
在新玛特、百货大楼同款的mp3的单价相同,书包单价也相同,mp3和书包单价之和是452元,且mp3的单价比书包单价的4倍少8元,你能算出mp3和书包单价各是多少元吗?
解:设书包单价为x元,mp3单价为y元,由题意得:
解得:
答:书包单价92元,随身听单价360元。
三、购物问题
1、育才学校去年有学生3100名,今年比去年增加4.4%,其中寄宿学生增加了6%,走读学生减少了2%.问该校去年有寄宿学生与走读学生各多少名 设去年有寄宿学生x名,走读学生y名,列出方程组
寄宿学生 走读学生 学生总数
去年
今年
x
y
3100
(1+6%)x
(1-2%)y
3100 ×
(1+4.4%)
2、一、二两班共有100名学生,他们的体育达标率(达到标准的百分率)为81%。如果一班学生的体育达标率为87.5%,二班的达标率为75%,那么一、二两班的学生数各是多少 设一班学生有x名、二班学生有y名,列出方程组
一班 二班 两班总和
学生数
达标学生数
x
87.5%x
y
75%y
100
81%×100
3、某公司用30000元购进甲乙两种货物.货物卖出后,甲种货物获利10%,乙种货物获利11%,共得利润3150元,问两种货物各进多少钱的货 设甲种货物进x元的货,乙种货物进 y元的货.列出方程组
甲种 乙种 总和
进货钱 X y
获利
30000
10%X
11%y
3150
4、用含糖分别为35%和40%的两种糖水混合,配制成含糖36%的糖水50千克,每种糖水应各取多少千克 设应取35%的糖水x千克,40%的糖水Y千克.列出方程组。
35%的糖水 40%的糖水 总和
糖水重量 X Y
含糖量
50
35%X
40%Y
50×36%
5、甲、乙两人从相距36千米的两地相向而行,如甲比乙先走2时,那么他们在乙出发2.5时后相遇;如果乙比甲先走2时,那么他们在甲出发3时后相遇,甲、乙两人每时各走多少千米 设甲、乙两人每时分别行走x千米,y千米。列出方程组
甲走的路程 乙走的路程
甲乙行走的路程和
甲先2小时
乙先2小时
(2+2.5)x
2.5y
36
36
3x
(2+3)y
做课本 P233 习题 2、3
列方程解应用题步骤
1·审题 (找等量关系)2·设未知数 3·列方程 4·解方程 5·检验·作答
关键:找等量关系. 列方程
做课本 P228习题 1(1、2)
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
