《相交线》(课件) 数学四年级上册(共22张PPT)人教版
文档属性
| 名称 | 《相交线》(课件) 数学四年级上册(共22张PPT)人教版 | 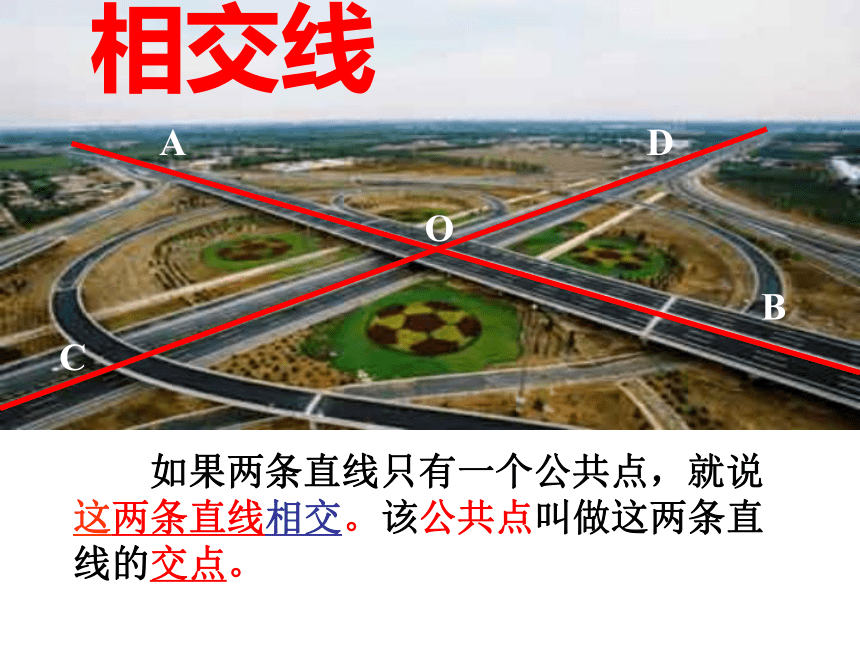 | |
| 格式 | pptx | ||
| 文件大小 | 642.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 07:55:41 | ||
图片预览

文档简介
(共22张PPT)
A
B
C
D
O
如果两条直线只有一个公共点,就说这两条直线相交。该公共点叫做这两条直线的交点。
相交线
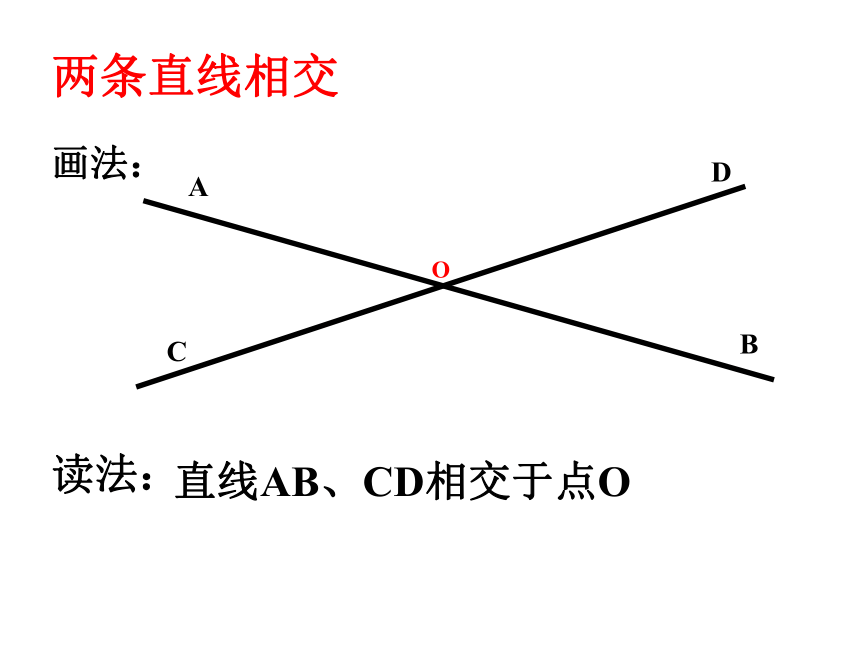
两条直线相交
画法:
A
B
C
D
O
读法:
直线AB、CD相交于点O
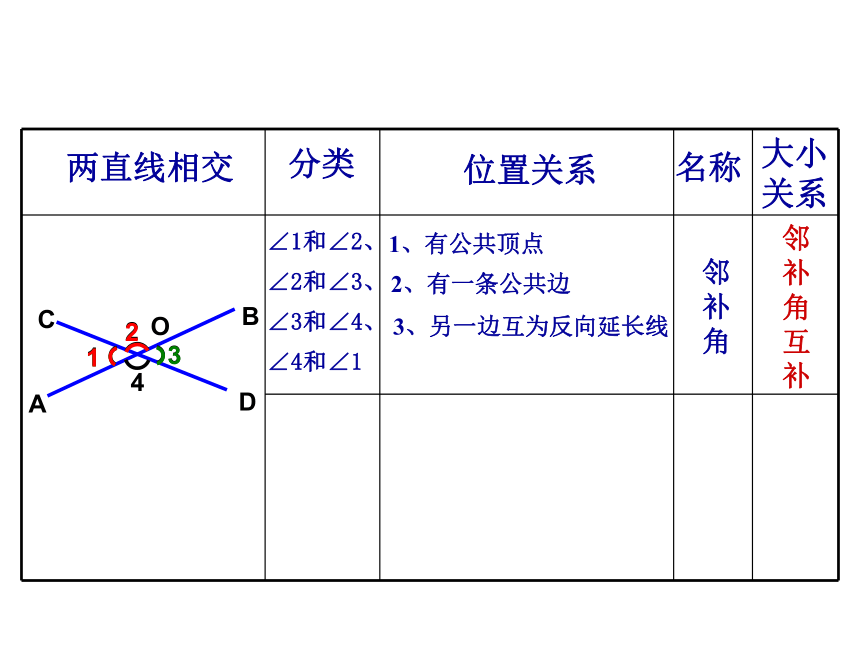
分类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
1、有公共顶点
位置关系
邻补角
邻补角互补
2、有一条公共边
3、另一边互为反向延长线
两直线相交
名称
大小关系
B
A
C
D
O
1
2
3
4
1
3
1
2
1
2
3
4
A
B
C
D
O
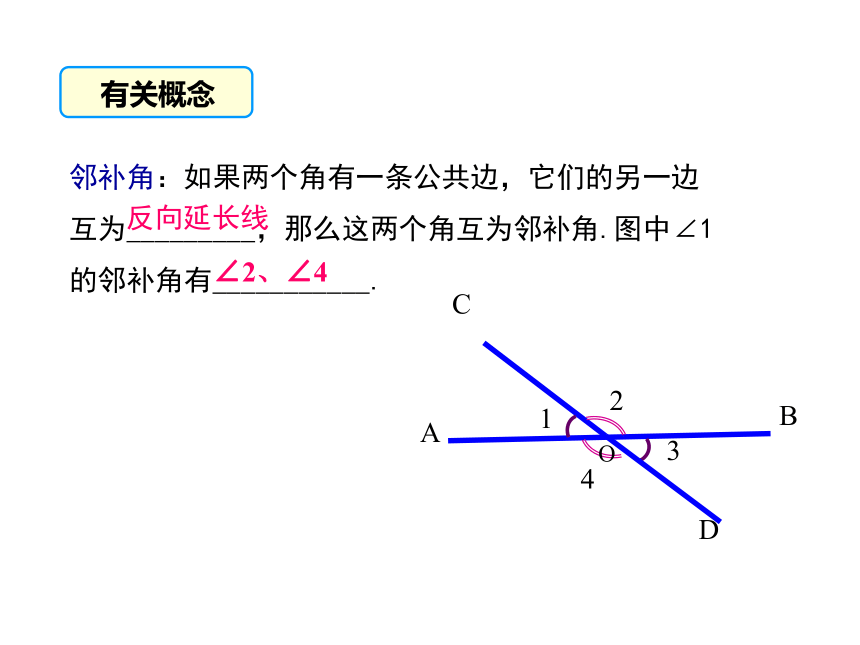
邻补角:如果两个角有一条公共边,它们的另一边互为_________,那么这两个角互为邻补角.图中∠1的邻补角有___________.
反向延长线
∠2、∠4
有关概念
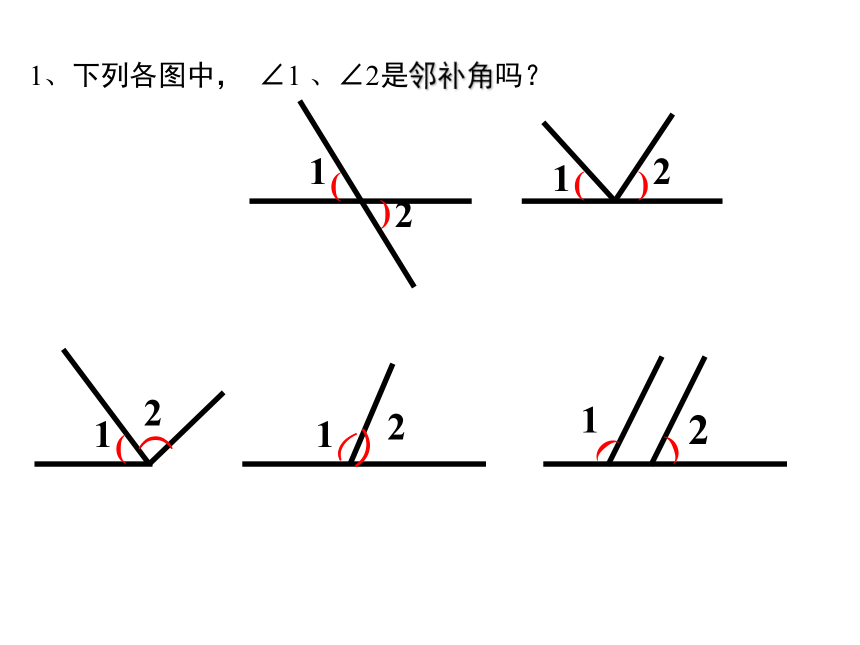
1、下列各图中, ∠1 、∠2是邻补角吗?
(
)
1
2
(
)
2
1
(
1
(
2
(
)
1
2
(
)
1
2
1、有公共顶点
分类
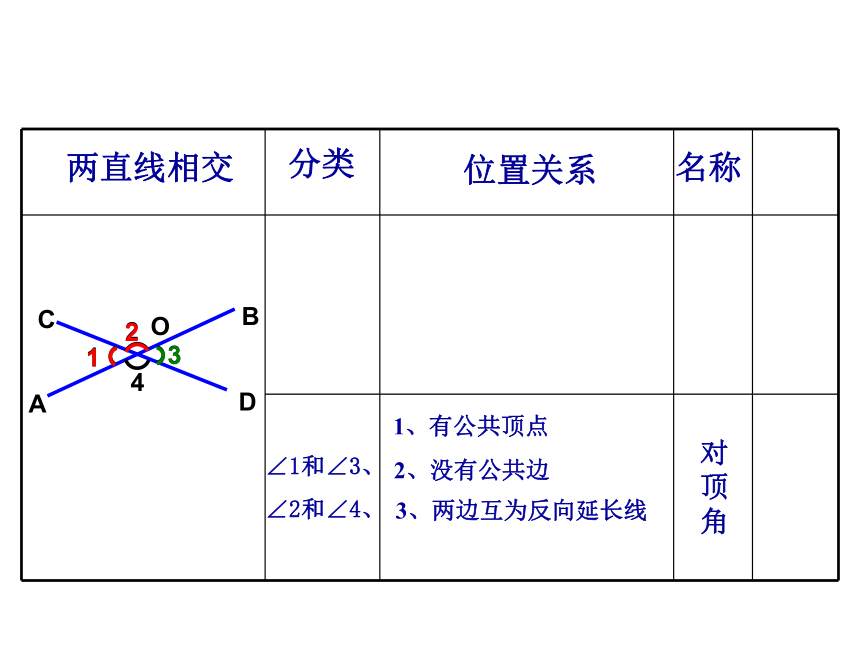
∠1和∠3、
∠2和∠4、
位置关系
对顶角
2、没有公共边
两直线相交
3、两边互为反向延长线
名称
B
A
C
D
O
1
2
3
4
1
3
1
2
1
2
3
4
A
B
C
D
O
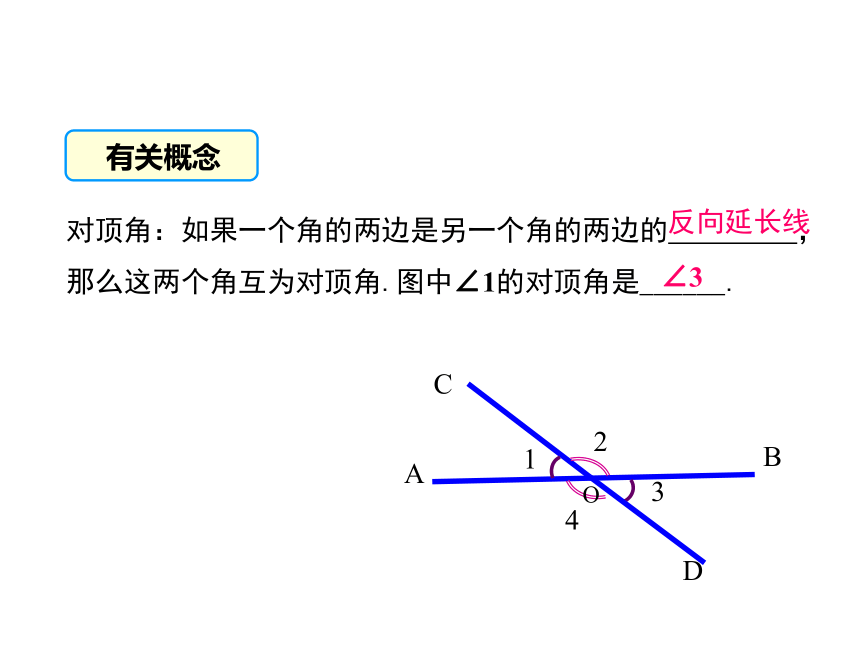
对顶角:如果一个角的两边是另一个角的两边的 ,那么这两个角互为对顶角.图中∠1的对顶角是______.
反向延长线
∠3
有关概念
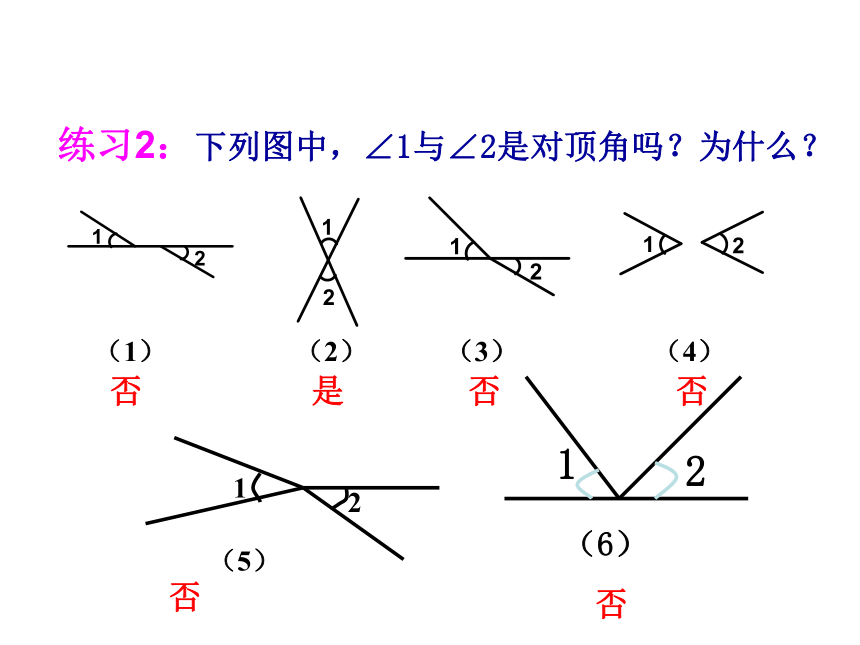
练习2:下列图中,∠1与∠2是对顶角吗?为什么?
否
是
否
否
(1)
(2)
(3)
(4)
1
2
(5)
否
否
1
2
(6)
O
A
B
C
D
3
1
O
A
B
C
D
4
3
2
1
已知:直线AB与CD相交于O点(如图),试说明:∠1=∠3、 ∠2=∠4.
解:∵直线AB与CD相交于O点,
∴∠1+∠2=180°
∠2+∠3=180°,
∴∠1=∠3.
同理可得:∠2=∠4.
(邻补角定义)
(同角的补角相等)
O
A
B
C
D
3
1
∵直线AB与CD相交于O点
∴∠1=∠3(对顶角相等)
3、如图,直线AB,CD相交于点O, ∠EOC=70°,
OA平分∠EOC,求∠BOD的度数。
A
B
C
D
E
O
1、有公共顶点
分类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、
∠2和∠4、
1、有公共顶点
位置关系
邻补角
对顶角
邻补角互补
2、有一条公共边
3、另一边互为反向延长线
2、没有公共边
两直线相交
3、两边互为反向延长线
名称
大小关系
对顶角相等
B
A
C
D
O
1
2
3
4
1
3
1
2
4.如图,直线AB.CD.EF相交于点O,则
1).∠AOC的对顶角是____________
2).∠AOD的对顶角是____________
3).∠BOC的邻补角是____________
4).∠BOE的邻补角是____________
A
B
C
D
E
F
O
∠BOD
∠BOC
∠AOC和∠BOD
∠AOE和∠BOF
a
b
)
(
1
3
4
2
)
(
5:如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠4的度数。
∵∠3=∠1
∠1=40°
∴∠3=40° (对顶角相等)
解:
∴∠2=180°-∠1=140°
∴∠4=∠2=140° (邻补角定义)
变式1:若∠2是∠1的3倍,求∠3的度数?
变式2:若∠2-∠1=400, 求∠4的度数?
用代数的方法(列方程)解决几何问题是比较有效的!
1、有公共顶点
分类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、
∠2和∠4、
1、有公共顶点
位置关系
邻补角
对顶角
邻补角互补
2、有一条公共边
3、另一边互为反向延长线
2、没有公共边
两直线相交
3、两边互为反向延长线
名称
大小关系
对顶角相等
B
A
C
D
O
1
2
3
4
1
3
1
2
1、若∠1与∠2是对顶角,∠1=160,则∠2=______0;
若 ∠3与∠4是邻补角,则∠3+∠4 =______0
180
180
2、若∠1与∠2为对顶角,∠1与∠3互补,则 ∠2+∠3= 0
16
练习:
3、图中是对顶角量角器,你能说出用它测量角的原理吗?
答:对顶角相等。
解:∵∠DOB=∠ ,( )
=80°(已知)
∴∠DOB= °(等量代换)
又∵∠1=30°( )
∴∠2=∠ -∠ = - = °
4、一个角的对顶角有 个,邻补角最多有
个,而补角则可以有 个。
6、如图,直线AB、CD相交于O,∠AOC=80°∠1=30°;求∠2的度数.
A
C
B
D
E
1
一
两
无数
AOC
∠AOC
DOB
1
80°
30°
50
对顶角相等
已知
80
5、右图中∠AOC的对顶角是 ,
邻补角是 .
∠DOB
∠AOD和∠COB
2
)
)
O
7、如右图中直线AB、CD交于O, OE是∠BOC的平分线且∠BOE=50度,那么∠AOE=( )度
(A)80;(B)100;(C)130(D)150。
A
B
C
D
O
E
C
8:如图,直线a、b相交。
(1) ∠ 1=400, 求∠2,∠3,∠4的度数。
(2) ∠1:∠2=2:7 ,求各角的度数。
∠2=180°-∠1
=180°- 40°
解:(1)由邻补角的定义,可得
=140°
由对顶角相等,可得
∠3=∠1=40°
∠4=∠2=140°
9、如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=700,求∠BOD,∠BOC的度数。
解:∵OA平分∠EOC,∠EOC= 700
∴∠AOC=350
∠BOC= 180°-∠AOC
= 180°- 35°
= 145°(邻补角定义)
∴∠BOD=∠AOC=350 (对顶角相等)
谢谢观看
A
B
C
D
O
如果两条直线只有一个公共点,就说这两条直线相交。该公共点叫做这两条直线的交点。
相交线
两条直线相交
画法:
A
B
C
D
O
读法:
直线AB、CD相交于点O
分类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
1、有公共顶点
位置关系
邻补角
邻补角互补
2、有一条公共边
3、另一边互为反向延长线
两直线相交
名称
大小关系
B
A
C
D
O
1
2
3
4
1
3
1
2
1
2
3
4
A
B
C
D
O
邻补角:如果两个角有一条公共边,它们的另一边互为_________,那么这两个角互为邻补角.图中∠1的邻补角有___________.
反向延长线
∠2、∠4
有关概念
1、下列各图中, ∠1 、∠2是邻补角吗?
(
)
1
2
(
)
2
1
(
1
(
2
(
)
1
2
(
)
1
2
1、有公共顶点
分类
∠1和∠3、
∠2和∠4、
位置关系
对顶角
2、没有公共边
两直线相交
3、两边互为反向延长线
名称
B
A
C
D
O
1
2
3
4
1
3
1
2
1
2
3
4
A
B
C
D
O
对顶角:如果一个角的两边是另一个角的两边的 ,那么这两个角互为对顶角.图中∠1的对顶角是______.
反向延长线
∠3
有关概念
练习2:下列图中,∠1与∠2是对顶角吗?为什么?
否
是
否
否
(1)
(2)
(3)
(4)
1
2
(5)
否
否
1
2
(6)
O
A
B
C
D
3
1
O
A
B
C
D
4
3
2
1
已知:直线AB与CD相交于O点(如图),试说明:∠1=∠3、 ∠2=∠4.
解:∵直线AB与CD相交于O点,
∴∠1+∠2=180°
∠2+∠3=180°,
∴∠1=∠3.
同理可得:∠2=∠4.
(邻补角定义)
(同角的补角相等)
O
A
B
C
D
3
1
∵直线AB与CD相交于O点
∴∠1=∠3(对顶角相等)
3、如图,直线AB,CD相交于点O, ∠EOC=70°,
OA平分∠EOC,求∠BOD的度数。
A
B
C
D
E
O
1、有公共顶点
分类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、
∠2和∠4、
1、有公共顶点
位置关系
邻补角
对顶角
邻补角互补
2、有一条公共边
3、另一边互为反向延长线
2、没有公共边
两直线相交
3、两边互为反向延长线
名称
大小关系
对顶角相等
B
A
C
D
O
1
2
3
4
1
3
1
2
4.如图,直线AB.CD.EF相交于点O,则
1).∠AOC的对顶角是____________
2).∠AOD的对顶角是____________
3).∠BOC的邻补角是____________
4).∠BOE的邻补角是____________
A
B
C
D
E
F
O
∠BOD
∠BOC
∠AOC和∠BOD
∠AOE和∠BOF
a
b
)
(
1
3
4
2
)
(
5:如图,直线a、b相交,∠1=40°,求 ∠2、∠3、∠4的度数。
∵∠3=∠1
∠1=40°
∴∠3=40° (对顶角相等)
解:
∴∠2=180°-∠1=140°
∴∠4=∠2=140° (邻补角定义)
变式1:若∠2是∠1的3倍,求∠3的度数?
变式2:若∠2-∠1=400, 求∠4的度数?
用代数的方法(列方程)解决几何问题是比较有效的!
1、有公共顶点
分类
∠1和∠2、∠2和∠3、∠3和∠4、∠4和∠1
∠1和∠3、
∠2和∠4、
1、有公共顶点
位置关系
邻补角
对顶角
邻补角互补
2、有一条公共边
3、另一边互为反向延长线
2、没有公共边
两直线相交
3、两边互为反向延长线
名称
大小关系
对顶角相等
B
A
C
D
O
1
2
3
4
1
3
1
2
1、若∠1与∠2是对顶角,∠1=160,则∠2=______0;
若 ∠3与∠4是邻补角,则∠3+∠4 =______0
180
180
2、若∠1与∠2为对顶角,∠1与∠3互补,则 ∠2+∠3= 0
16
练习:
3、图中是对顶角量角器,你能说出用它测量角的原理吗?
答:对顶角相等。
解:∵∠DOB=∠ ,( )
=80°(已知)
∴∠DOB= °(等量代换)
又∵∠1=30°( )
∴∠2=∠ -∠ = - = °
4、一个角的对顶角有 个,邻补角最多有
个,而补角则可以有 个。
6、如图,直线AB、CD相交于O,∠AOC=80°∠1=30°;求∠2的度数.
A
C
B
D
E
1
一
两
无数
AOC
∠AOC
DOB
1
80°
30°
50
对顶角相等
已知
80
5、右图中∠AOC的对顶角是 ,
邻补角是 .
∠DOB
∠AOD和∠COB
2
)
)
O
7、如右图中直线AB、CD交于O, OE是∠BOC的平分线且∠BOE=50度,那么∠AOE=( )度
(A)80;(B)100;(C)130(D)150。
A
B
C
D
O
E
C
8:如图,直线a、b相交。
(1) ∠ 1=400, 求∠2,∠3,∠4的度数。
(2) ∠1:∠2=2:7 ,求各角的度数。
∠2=180°-∠1
=180°- 40°
解:(1)由邻补角的定义,可得
=140°
由对顶角相等,可得
∠3=∠1=40°
∠4=∠2=140°
9、如图,已知直线AB,CD相交于点O,OA平分∠EOC,∠EOC=700,求∠BOD,∠BOC的度数。
解:∵OA平分∠EOC,∠EOC= 700
∴∠AOC=350
∠BOC= 180°-∠AOC
= 180°- 35°
= 145°(邻补角定义)
∴∠BOD=∠AOC=350 (对顶角相等)
谢谢观看
