人教版八年级上册数学13.4课题学习最短路径训练(word版含答案)
文档属性
| 名称 | 人教版八年级上册数学13.4课题学习最短路径训练(word版含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 814.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 00:00:00 | ||
图片预览


文档简介
人教版八年级上册数学13.4课题学习最短路径训练
一、单选题
1.如图所示,直线l是一条河的河岸,P,Q是河同侧的水产的生产基地,现从河岸某点M处分别派出两辆水产车运送水产如下有四种运输方案,则运输路程合理且最短的是( )
A. B.
C. D.
2.如图,在等边三角形中,,分别是,的中点,点是线段上的一个动点,当的周长最小时,点的位置在( )
A.点处 B.点处
C.的中点处 D.三条高的交点处
3.如图,正方体的棱长为2,B为一条棱的中点.已知蚂蚁沿正方体的表面从A点出发,到达B点,则它运动的最短路程为( )
A. B.4 C. D.5
4.在中,,,于点,且,若点在边上移动,则的最小值是( )
A.4.5 B.4.6 C.4.7 D.4.8
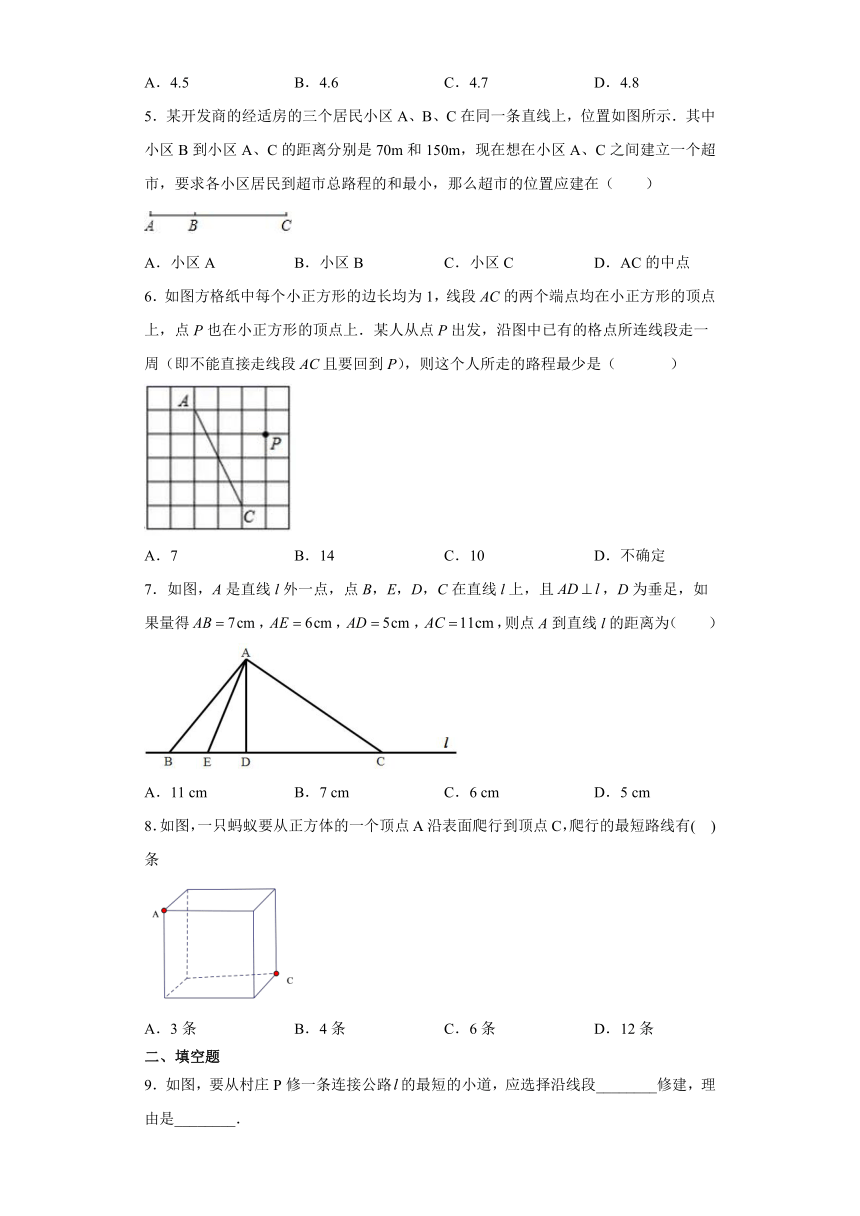
5.某开发商的经适房的三个居民小区A、B、C在同一条直线上,位置如图所示.其中小区B到小区A、C的距离分别是70m和150m,现在想在小区A、C之间建立一个超市,要求各小区居民到超市总路程的和最小,那么超市的位置应建在( )
A.小区A B.小区B C.小区C D.AC的中点
6.如图方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上,点P也在小正方形的顶点上.某人从点P出发,沿图中已有的格点所连线段走一周(即不能直接走线段AC且要回到P),则这个人所走的路程最少是( )
A.7 B.14 C.10 D.不确定
7.如图,A是直线l外一点,点B,E,D,C在直线l上,且,D为垂足,如果量得,,,,则点A到直线l的距离为( )
A.11 cm B.7 cm C.6 cm D.5 cm
8.如图,一只蚂蚁要从正方体的一个顶点A沿表面爬行到顶点C,爬行的最短路线有( )条
A.3条 B.4条 C.6条 D.12条
二、填空题
9.如图,要从村庄P修一条连接公路的最短的小道,应选择沿线段________修建,理由是________.
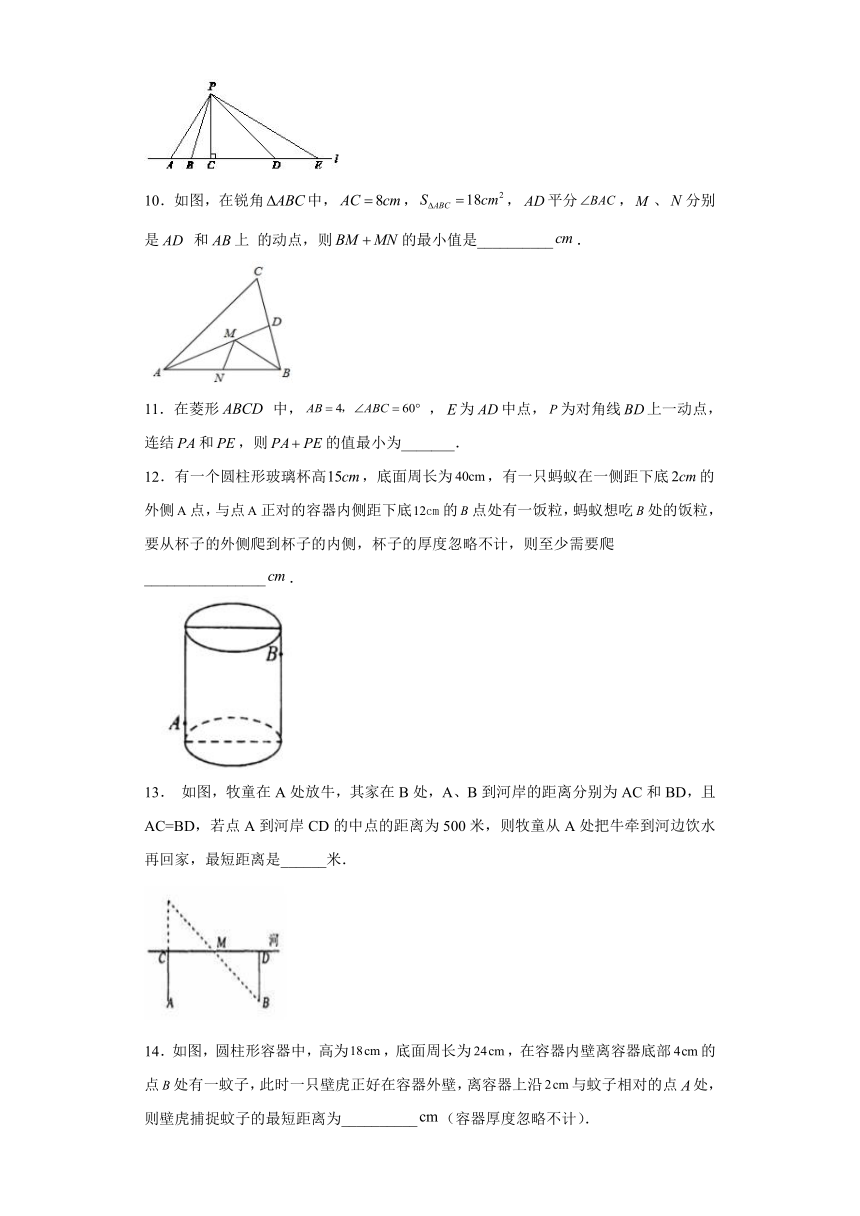
10.如图,在锐角中,,,平分,、分别是 和上 的动点,则的最小值是__________.
11.在菱形 中, ,为中点,为对角线上一动点,连结和,则的值最小为_______.
12.有一个圆柱形玻璃杯高,底面周长为,有一只蚂蚁在一侧距下底的外侧点,与点正对的容器内侧距下底的点处有一饭粒,蚂蚁想吃处的饭粒,要从杯子的外侧爬到杯子的内侧,杯子的厚度忽略不计,则至少需要爬________________.
13. 如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC和BD,且AC=BD,若点A到河岸CD的中点的距离为500米,则牧童从A处把牛牵到河边饮水再回家,最短距离是______米.
14.如图,圆柱形容器中,高为,底面周长为,在容器内壁离容器底部的点处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿与蚊子相对的点处,则壁虎捕捉蚊子的最短距离为__________(容器厚度忽略不计).
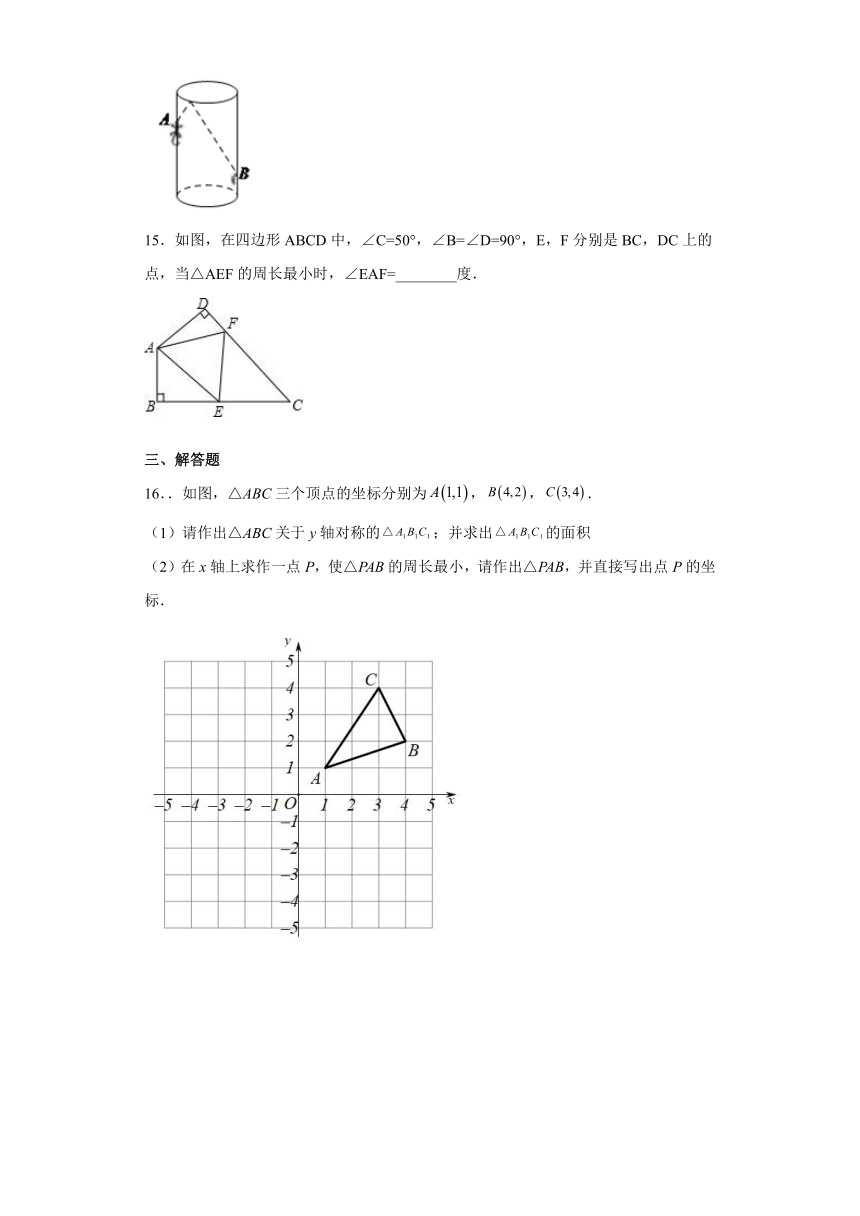
15.如图,在四边形ABCD中,∠C=50°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF=________度.
三、解答题
16..如图,△ABC三个顶点的坐标分别为,,.
(1)请作出△ABC关于y轴对称的;并求出的面积
(2)在x轴上求作一点P,使△PAB的周长最小,请作出△PAB,并直接写出点P的坐标.
17.如图,方格纸中每个小方格都是边长为1个单位的正方形,已知的三个顶点在格点上.
(1)画出,使它与关于直线a对称;
(2)求出的面积;
(3)在直线a上画出点P,使最小
18.如图,BA、BC是两条公路,在两条公路夹角内部的点P处有一油库,若在两公路上分别建个加油站,并使运油的油罐车从油库出发先到一加油站,再到另一加油站,最后回到油库的路程最短,则加油站应如何选址?
19.已知,如图:在平面直角坐标系中,O为坐标原点,四边形是长方形,点A C D的坐标分别为,,,点P从点O出发,以每秒1单位长度的速度沿运动,点P的运动时间为t秒.
(1)当时,P点坐标为___________;
(2)当时,有最小值吗?如果有,请算出该最小值,如果没有,请说明理由;
(3)当t为何值时,是腰长为5的等腰三角形?若存在,直接写出t的值,若没有,请说明理由.
参考答案
1.B
根据“将军饮马”模型求最短路线题型,作点P关于直线l的对称点,连接Q交直线l于点M,利用两点之间线段最短和线段垂直平分线的性质作图即可,
故选:B.
2.D
解:连接BP,
∵△ABC是等边三角形,D是BC的中点,
∴AD是BC的垂直平分线,
∴PB=PC,
当PC+PE的长最小时,即PB+PE最小
则此时点B、P、E在同一直线上,
又∵BE为中线,△ABC是等边三角形
∴点P为△ABC的三条中线的交点,也就是△ABC的三条高的交点.
故选:D
3.C
解:如图,它运动的最短路程AB= =
故选:C
4.D
由题意得:当BP⊥AC时,的值最小,
∵,
∴,
解得BP=,
故选:D.
5.B
解:设超市为点P,
∵P点在A、C 之间,
∴AP+BP+CP是超市到小区居民总路程的和,
∵AP+CP=AC,
∴当PB最短时,即P点与B点重合时,AP+BP+CP=AC,此时市到小区居民总路程的和最小,
故选:B.
6.B
如图,这个人所走的路程是图中的矩形,
周长为2(3+4)=14
故选B.
7.D
∵AD=5cm,∴点A到直线l的距离是5cm.
故选D.
8.C
根据两点之间线段最短知A到C的最短路线是A、C展开在同一平面上为两正方形组成的长方形对角时,连接AC最短,
①前面和下面展开在一起时,连接AC为爬行的最短路线;
②前面和右面展开在一起时,连接AC为爬行的最短路线;
③上面和后面展开在一起时,连接AC为爬行的最短路线;
④上面和右面展开在一起时,连接AC为爬行的最短路线;
⑤左面和后面展开在一起时,连接AC为爬行的最短路线;
⑥左面和下面展开在一起时,连接AC为爬行的最短路线;
共6种,故选C.
9.PC 垂线段最短
解:∵从直线外一点到这条直线上各点所连线段中,垂线段最短,
∴过点P作PC⊥l于点C,这样做的理由是垂线段最短.
故答案为:PC,垂线段最短.
10.
解:作N关于AD的对称点R,作AC边上的高BE(E在AC上)
∵平分,△ABC是锐角三角形
∴R必在AC上
∵N关于AD的对称点是R
∴MN=MR
∴BM+MN=BM+MR
∴BM+MN=BR≥BE(垂线段最短)
∵,
∴=18
∴BE=cm
即BM+MN的最小值是cm.
故答案为.
11.2
作点E′和E关于BD对称.则连接AE′交BD于点P,
∵四边形ABCD是菱形,AB=4,E为AD中点,
∴点E′是CD的中点,
∴DE′=DC=×4=2,AE′⊥DC,
∴AE′=.
故答案为2.
12.
解:
如图:过沿上沿B点的对称点B′,作AC⊥BB′于C,
∵高15cm,底面周长为40cm,有一只蚂蚁在一侧距下底2cm的外侧A点,与点A正对的容器内侧距下底12cm的B点处有一饭粒,
此时蚂蚁正好在容器外壁,离容器上沿3cm与饭粒相对的点B处,
∴依题意得:
cm,
cm,
连接A B′,则A B′即为最短距离,
故答案为.
13.1000
【详解】
作出A的对称点A′,连接A′B与CD相交于M,则牧童从A处把牛牵到河边饮水再回家,最短距离是A′B的长.易得△A′CM≌△BDM,AC=BD,所以A′C=BD,则A′C /BD ="CM" /MD ,
所以CM=DM,M为CD的中点,
由于A到河岸CD的中点的距离为500米,
所以A′到M的距离为500米,
A′B=1000米.
故最短距离是1000米.
14.20
∵高为18cm,底面周长为24cm,在容器内壁离容器底部2cm的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿2cm与蚊子相对的点A处,
∴A′D=12cm,BD=16cm,
∴在直角△A′DB中,A′B==20(cm).
故答案是:20.
15.80°
解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于E,交CD于F,则A′A″即为△AEF的周长最小值.作DA延长线AH,
∵∠C=50°,
∴∠DAB=130°,
∴∠HAA′=50°,
∴∠A′+∠A″=∠HAA′=50°,
∵∠A′=∠EAB,∠A″=∠FAD,
∴∠EAB+∠FAD=50°,
∴∠EAF=130°-50°=80°,
故答案为80°.
16.
(1)如图所示,即为所求;
的面积为:;
故答案为:3.5.
(2)如图所示,作点A关于x轴的对称点 ,则;连接 ,它与x轴的交点就是所求作的点P,此时 最小,即为所求,由图知点的坐标为.
17.
(1)如图,△A1B1C1即为所求.
(2)=2×2-×1×2×2-×1×1=.
(3)如图,连接C1A(或A1C)与直线a交于点P,则点P即为所求.
18.
解:如图所示:C、D点即为所求.
19.
解:(1)由题意可得,
当t=5时,点P在BC上,且PC=5-4=1,
又∵OC=4,
∴点P的坐标为(1,4);
(2)当t>4时,
点P在BC或AB上,
当点P在BC上时,作点D关于直线CB的对称点D′,连接OD′与BC交于点P,则点P即为所求,
如图一所示,
∵四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),
∴点D′(5,8),
∴OP+PD的最小值为OD′,即OD′==;
当点P在AB上时,当点P与点A重合时,OP+PD最小,
∴OP+PD的最小值为OA+AD=9+4=13>;
综上:OP+PD的最小值为;
(3)当,7,12或14时,是腰长为5的等腰三角形,
理由:如图二所示,
当时,
点,点,
,
,
,
;
当时,
,
,
,
;
当时,
,
,
,
;
当时,
,
,
点,点,
,
;
由上可得,当,7,12或14时,是腰长为5的等腰三角形.
一、单选题
1.如图所示,直线l是一条河的河岸,P,Q是河同侧的水产的生产基地,现从河岸某点M处分别派出两辆水产车运送水产如下有四种运输方案,则运输路程合理且最短的是( )
A. B.
C. D.
2.如图,在等边三角形中,,分别是,的中点,点是线段上的一个动点,当的周长最小时,点的位置在( )
A.点处 B.点处
C.的中点处 D.三条高的交点处
3.如图,正方体的棱长为2,B为一条棱的中点.已知蚂蚁沿正方体的表面从A点出发,到达B点,则它运动的最短路程为( )
A. B.4 C. D.5
4.在中,,,于点,且,若点在边上移动,则的最小值是( )
A.4.5 B.4.6 C.4.7 D.4.8
5.某开发商的经适房的三个居民小区A、B、C在同一条直线上,位置如图所示.其中小区B到小区A、C的距离分别是70m和150m,现在想在小区A、C之间建立一个超市,要求各小区居民到超市总路程的和最小,那么超市的位置应建在( )
A.小区A B.小区B C.小区C D.AC的中点
6.如图方格纸中每个小正方形的边长均为1,线段AC的两个端点均在小正方形的顶点上,点P也在小正方形的顶点上.某人从点P出发,沿图中已有的格点所连线段走一周(即不能直接走线段AC且要回到P),则这个人所走的路程最少是( )
A.7 B.14 C.10 D.不确定
7.如图,A是直线l外一点,点B,E,D,C在直线l上,且,D为垂足,如果量得,,,,则点A到直线l的距离为( )
A.11 cm B.7 cm C.6 cm D.5 cm
8.如图,一只蚂蚁要从正方体的一个顶点A沿表面爬行到顶点C,爬行的最短路线有( )条
A.3条 B.4条 C.6条 D.12条
二、填空题
9.如图,要从村庄P修一条连接公路的最短的小道,应选择沿线段________修建,理由是________.
10.如图,在锐角中,,,平分,、分别是 和上 的动点,则的最小值是__________.
11.在菱形 中, ,为中点,为对角线上一动点,连结和,则的值最小为_______.
12.有一个圆柱形玻璃杯高,底面周长为,有一只蚂蚁在一侧距下底的外侧点,与点正对的容器内侧距下底的点处有一饭粒,蚂蚁想吃处的饭粒,要从杯子的外侧爬到杯子的内侧,杯子的厚度忽略不计,则至少需要爬________________.
13. 如图,牧童在A处放牛,其家在B处,A、B到河岸的距离分别为AC和BD,且AC=BD,若点A到河岸CD的中点的距离为500米,则牧童从A处把牛牵到河边饮水再回家,最短距离是______米.
14.如图,圆柱形容器中,高为,底面周长为,在容器内壁离容器底部的点处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿与蚊子相对的点处,则壁虎捕捉蚊子的最短距离为__________(容器厚度忽略不计).
15.如图,在四边形ABCD中,∠C=50°,∠B=∠D=90°,E,F分别是BC,DC上的点,当△AEF的周长最小时,∠EAF=________度.
三、解答题
16..如图,△ABC三个顶点的坐标分别为,,.
(1)请作出△ABC关于y轴对称的;并求出的面积
(2)在x轴上求作一点P,使△PAB的周长最小,请作出△PAB,并直接写出点P的坐标.
17.如图,方格纸中每个小方格都是边长为1个单位的正方形,已知的三个顶点在格点上.
(1)画出,使它与关于直线a对称;
(2)求出的面积;
(3)在直线a上画出点P,使最小
18.如图,BA、BC是两条公路,在两条公路夹角内部的点P处有一油库,若在两公路上分别建个加油站,并使运油的油罐车从油库出发先到一加油站,再到另一加油站,最后回到油库的路程最短,则加油站应如何选址?
19.已知,如图:在平面直角坐标系中,O为坐标原点,四边形是长方形,点A C D的坐标分别为,,,点P从点O出发,以每秒1单位长度的速度沿运动,点P的运动时间为t秒.
(1)当时,P点坐标为___________;
(2)当时,有最小值吗?如果有,请算出该最小值,如果没有,请说明理由;
(3)当t为何值时,是腰长为5的等腰三角形?若存在,直接写出t的值,若没有,请说明理由.
参考答案
1.B
根据“将军饮马”模型求最短路线题型,作点P关于直线l的对称点,连接Q交直线l于点M,利用两点之间线段最短和线段垂直平分线的性质作图即可,
故选:B.
2.D
解:连接BP,
∵△ABC是等边三角形,D是BC的中点,
∴AD是BC的垂直平分线,
∴PB=PC,
当PC+PE的长最小时,即PB+PE最小
则此时点B、P、E在同一直线上,
又∵BE为中线,△ABC是等边三角形
∴点P为△ABC的三条中线的交点,也就是△ABC的三条高的交点.
故选:D
3.C
解:如图,它运动的最短路程AB= =
故选:C
4.D
由题意得:当BP⊥AC时,的值最小,
∵,
∴,
解得BP=,
故选:D.
5.B
解:设超市为点P,
∵P点在A、C 之间,
∴AP+BP+CP是超市到小区居民总路程的和,
∵AP+CP=AC,
∴当PB最短时,即P点与B点重合时,AP+BP+CP=AC,此时市到小区居民总路程的和最小,
故选:B.
6.B
如图,这个人所走的路程是图中的矩形,
周长为2(3+4)=14
故选B.
7.D
∵AD=5cm,∴点A到直线l的距离是5cm.
故选D.
8.C
根据两点之间线段最短知A到C的最短路线是A、C展开在同一平面上为两正方形组成的长方形对角时,连接AC最短,
①前面和下面展开在一起时,连接AC为爬行的最短路线;
②前面和右面展开在一起时,连接AC为爬行的最短路线;
③上面和后面展开在一起时,连接AC为爬行的最短路线;
④上面和右面展开在一起时,连接AC为爬行的最短路线;
⑤左面和后面展开在一起时,连接AC为爬行的最短路线;
⑥左面和下面展开在一起时,连接AC为爬行的最短路线;
共6种,故选C.
9.PC 垂线段最短
解:∵从直线外一点到这条直线上各点所连线段中,垂线段最短,
∴过点P作PC⊥l于点C,这样做的理由是垂线段最短.
故答案为:PC,垂线段最短.
10.
解:作N关于AD的对称点R,作AC边上的高BE(E在AC上)
∵平分,△ABC是锐角三角形
∴R必在AC上
∵N关于AD的对称点是R
∴MN=MR
∴BM+MN=BM+MR
∴BM+MN=BR≥BE(垂线段最短)
∵,
∴=18
∴BE=cm
即BM+MN的最小值是cm.
故答案为.
11.2
作点E′和E关于BD对称.则连接AE′交BD于点P,
∵四边形ABCD是菱形,AB=4,E为AD中点,
∴点E′是CD的中点,
∴DE′=DC=×4=2,AE′⊥DC,
∴AE′=.
故答案为2.
12.
解:
如图:过沿上沿B点的对称点B′,作AC⊥BB′于C,
∵高15cm,底面周长为40cm,有一只蚂蚁在一侧距下底2cm的外侧A点,与点A正对的容器内侧距下底12cm的B点处有一饭粒,
此时蚂蚁正好在容器外壁,离容器上沿3cm与饭粒相对的点B处,
∴依题意得:
cm,
cm,
连接A B′,则A B′即为最短距离,
故答案为.
13.1000
【详解】
作出A的对称点A′,连接A′B与CD相交于M,则牧童从A处把牛牵到河边饮水再回家,最短距离是A′B的长.易得△A′CM≌△BDM,AC=BD,所以A′C=BD,则A′C /BD ="CM" /MD ,
所以CM=DM,M为CD的中点,
由于A到河岸CD的中点的距离为500米,
所以A′到M的距离为500米,
A′B=1000米.
故最短距离是1000米.
14.20
∵高为18cm,底面周长为24cm,在容器内壁离容器底部2cm的点B处有一蚊子,此时一只壁虎正好在容器外壁,离容器上沿2cm与蚊子相对的点A处,
∴A′D=12cm,BD=16cm,
∴在直角△A′DB中,A′B==20(cm).
故答案是:20.
15.80°
解:作A关于BC和CD的对称点A′,A″,连接A′A″,交BC于E,交CD于F,则A′A″即为△AEF的周长最小值.作DA延长线AH,
∵∠C=50°,
∴∠DAB=130°,
∴∠HAA′=50°,
∴∠A′+∠A″=∠HAA′=50°,
∵∠A′=∠EAB,∠A″=∠FAD,
∴∠EAB+∠FAD=50°,
∴∠EAF=130°-50°=80°,
故答案为80°.
16.
(1)如图所示,即为所求;
的面积为:;
故答案为:3.5.
(2)如图所示,作点A关于x轴的对称点 ,则;连接 ,它与x轴的交点就是所求作的点P,此时 最小,即为所求,由图知点的坐标为.
17.
(1)如图,△A1B1C1即为所求.
(2)=2×2-×1×2×2-×1×1=.
(3)如图,连接C1A(或A1C)与直线a交于点P,则点P即为所求.
18.
解:如图所示:C、D点即为所求.
19.
解:(1)由题意可得,
当t=5时,点P在BC上,且PC=5-4=1,
又∵OC=4,
∴点P的坐标为(1,4);
(2)当t>4时,
点P在BC或AB上,
当点P在BC上时,作点D关于直线CB的对称点D′,连接OD′与BC交于点P,则点P即为所求,
如图一所示,
∵四边形OABC是长方形,点A、C、D的坐标分别为A(9,0)、C(0,4),D(5,0),
∴点D′(5,8),
∴OP+PD的最小值为OD′,即OD′==;
当点P在AB上时,当点P与点A重合时,OP+PD最小,
∴OP+PD的最小值为OA+AD=9+4=13>;
综上:OP+PD的最小值为;
(3)当,7,12或14时,是腰长为5的等腰三角形,
理由:如图二所示,
当时,
点,点,
,
,
,
;
当时,
,
,
,
;
当时,
,
,
,
;
当时,
,
,
点,点,
,
;
由上可得,当,7,12或14时,是腰长为5的等腰三角形.
