2021-2022学年北师大版八年级数学上册7.5 三角形的内角和定理 同步测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版八年级数学上册7.5 三角形的内角和定理 同步测试卷(Word版含答案) |  | |
| 格式 | docx | ||
| 文件大小 | 334.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 18:07:14 | ||
图片预览

文档简介
7.5 三角形的内角和定理同步测试2021-2022学年北师大版八年级数学上册
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共12小题,共36分)
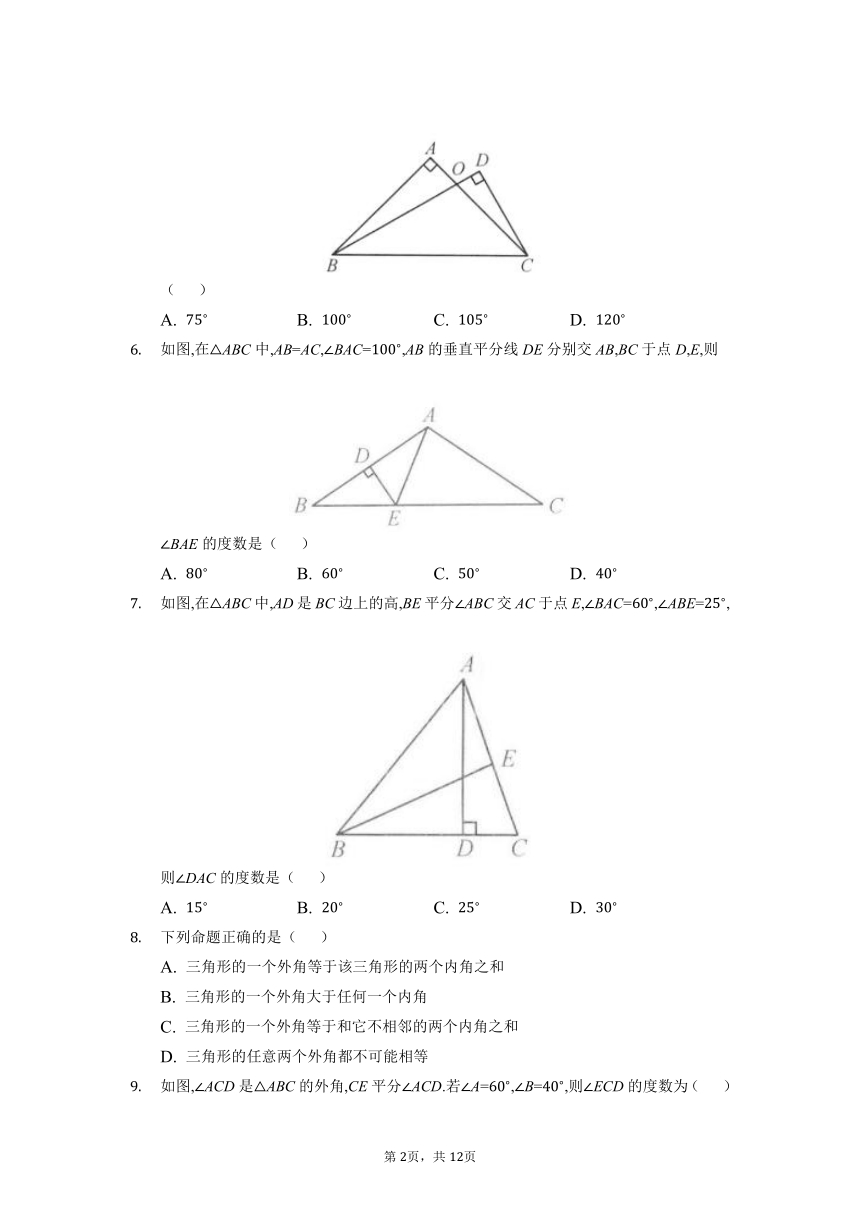
如图,在ABC中,A=,B=,则C的度数是( )
A. B. C. D.
如图,在ABC中,A=,B=,DEBC,则AED的度数是( )
A. B. C. D.
如图,ABCD,且DEC=,C=,则B的度数是( )
A. B. C. D.
如图,在ABC中,AB=AC,A=,BD是AC边上的高,则DBC的度数是( )
A.
B.
C.
D.
一副学生用的三角板按如图所示的方式放置,则AOD的度数为( )
A. B. C. D.
如图,在ABC中,AB=AC,BAC=,AB的垂直平分线DE分别交AB,BC于点D,E,则BAE的度数是( )
A. B. C. D.
如图,在ABC中,AD是BC边上的高,BE平分ABC交AC于点E,BAC=,ABE=,则DAC的度数是( )
A. B. C. D.
下列命题正确的是( )
A. 三角形的一个外角等于该三角形的两个内角之和
B. 三角形的一个外角大于任何一个内角
C. 三角形的一个外角等于和它不相邻的两个内角之和
D. 三角形的任意两个外角都不可能相等
如图,ACD是ABC的外角,CE平分ACD.若A=,B=,则ECD的度数为( )
A. B. C. D.
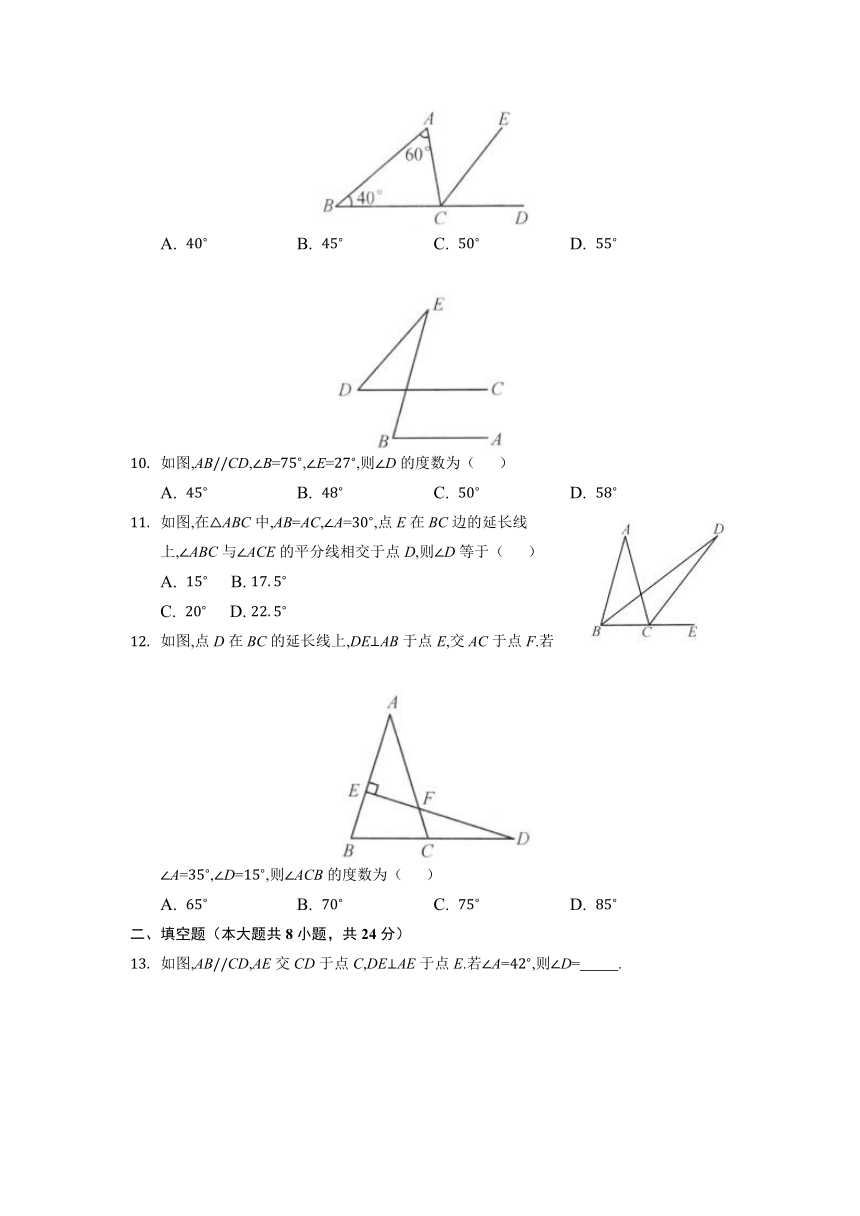
如图,ABCD,B=,E=,则D的度数为( )
A. B. C. D.
如图,在ABC中,AB=AC,A=,点E在BC边的延长线上,ABC与ACE的平分线相交于点D,则D等于( )
A. B.
C. D.
如图,点D在BC的延长线上,DEAB于点E,交AC于点F.若A=,D=,则ACB的度数为( )
A. B. C. D.
二、填空题(本大题共8小题,共24分)
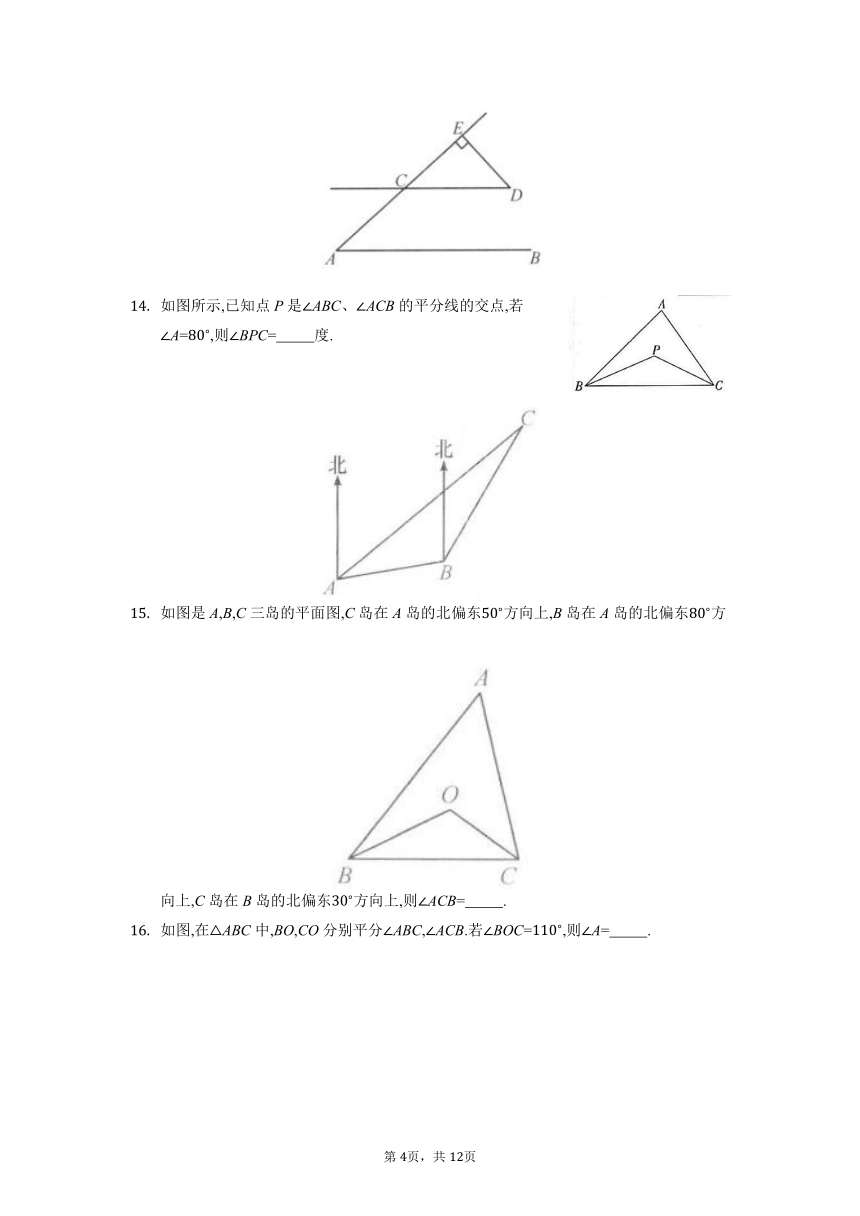
如图,ABCD,AE交CD于点C,DEAE于点E.若A=,则D= .
如图所示,已知点P是ABC、ACB的平分线的交点,若A=,则BPC= 度.
如图是A,B,C三岛的平面图,C岛在A岛的北偏东方向上,B岛在A岛的北偏东方向上,C岛在B岛的北偏东方向上,则ACB= .
如图,在ABC中,BO,CO分别平分ABC,ACB.若BOC=,则A= .
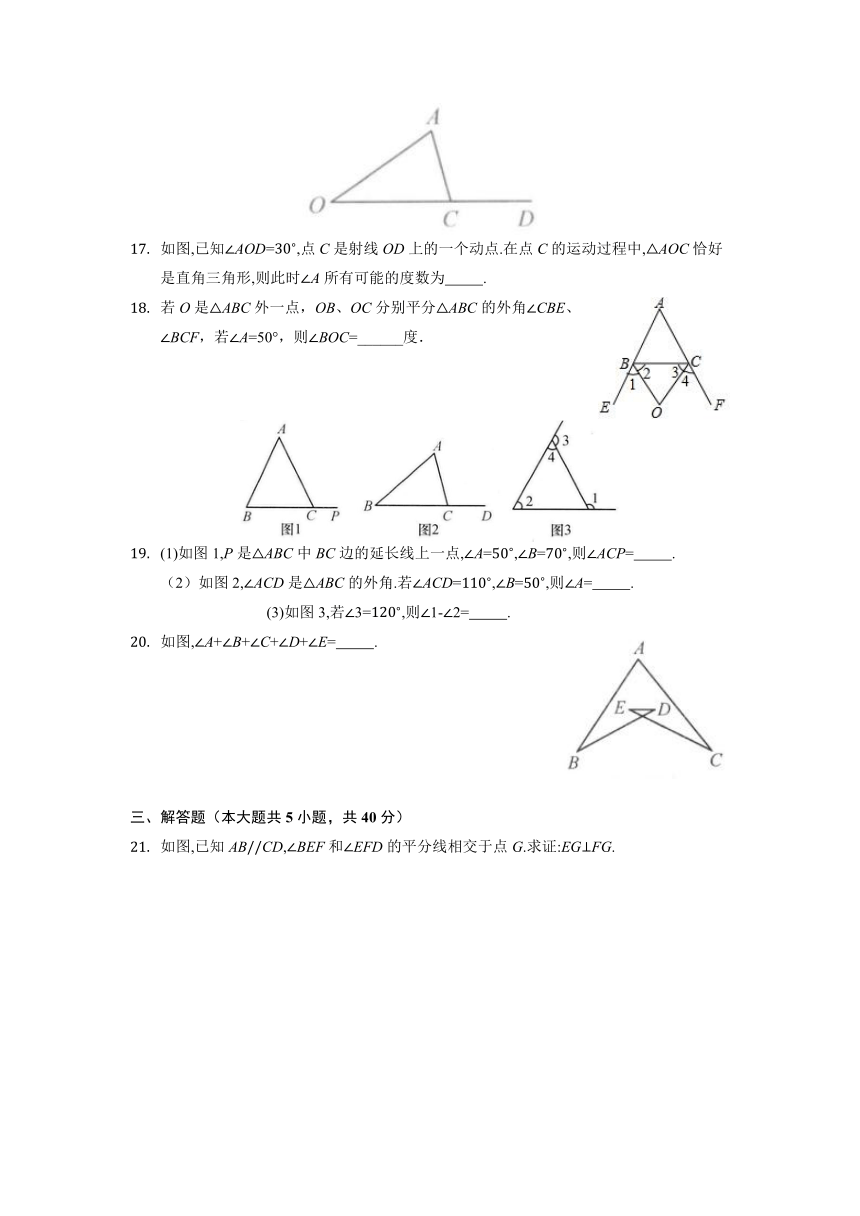
如图,已知AOD=,点C是射线OD上的一个动点.在点C的运动过程中,AOC恰好是直角三角形,则此时A所有可能的度数为 .
若O是△ABC外一点,OB、OC分别平分△ABC的外角∠CBE、∠BCF,若∠A=50°,则∠BOC=______度.
(1)如图1,P是ABC中BC边的延长线上一点,A=,B=,则ACP= .
(2)如图2,ACD是ABC的外角.若ACD=,B=,则A= .
(3)如图3,若3=,则1-2= .
如图,A+B+C+D+E= .
三、解答题(本大题共5小题,共40分)
如图,已知ABCD,BEF和EFD的平分线相交于点G.求证:EGFG.
如图,在中,AD⊥BC于点D,AE平分∠BAC,
(1)若∠B-∠C=30°,求∠DAE的度数.
(2)若B-C=(B>C),求DAE的度数.(用含的代数式表示)
如图1,线段AB,CD相交于点O,连接AD,CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,DAB和BCD的平分线AP和CP相交于点P,且与CD,AB分别相交于点M,N.
(1)直接写出图1中A,B,C,D之间的数量关系: .
(2)在图2中,若D=,B=,试求P的度数.
(3)当图2中D和B为任意角时,其他条件不变,P与D,B之间存在着怎样的数量关系 (直接写出结论即可)
一个零件的形状如图所示,规定:A=,B=,C=.李叔叔量得BDC=,判定这个零件不合格,你能说出其中的道理吗
如图,在ABC中,点E在AC上,AEB=ABC.
(1)图1中,作BAC的平分线AD,分别交CB, BE于D,F两点.求证:EFD=ADC.
(2)图2中,作ABC的外角BAG的平分线AD,分别交CB,BE的延长线于D,F两点.试探究(1)中结论是否仍成立,为什么
1.【答案】B
2.【答案】D
3.【答案】B
4.【答案】A
5.【答案】C
6.【答案】D
7.【答案】B
8.【答案】C
9.【答案】C
10.【答案】B
11.【答案】A
12.【答案】B
13.【答案】
14.【答案】130
15.【答案】
16.【答案】
17.【答案】或
18.【答案】65
19.【答案】
20.【答案】
21.【答案】证明:ABCD,
BEF+EFD=.
BEF和EFD的平分线交于点G,
FEG=BEF,EFG=EFD.
FEG+EFG=(BEF+EFD)=.
FEG+EFG+G=,
G=.
EGFG.
22.【答案】解:(1)ADBC,
ADC=.
AE平分BAC,
EAC=BAC.
而BAC=-B-C,
EAC=-B-C.
DAC=-C,
DAE=DAC-EAC=-C-(-B-C)= (B-C)=.
(2)ADBC,
ADC=.
AE平分BAC,
EAC=BAC.
又BAC=-B-C,
EAC=-B-C.
DAC=-C,
DAE= DAC-EAC=-C-(-B-C)= (B-C).
B-C=(B>C),
DAE=.
23.【答案】解:(1)A+D=C+B
(2)D+1+2=B+3+4,1=2,3=4,
+22=+24.
4-2=
B+4=P+2,
P=B+4-2=+=.
(3)P=.
24.【答案】解:连接AD并延长至点E,
BDE=B+BAD,CDE= C+CAD.
BAC=,B=,C=,
BDC= BDE+CDE=B+BAD+CAD+C=B+BAC+ C=++=.
,
这个零件不合格.
25.【答案】解:(1)证明:AD平分BAC,
BAD=DAC.
又AEB= ABC,
DAC+AEB=ABC+BAD,
即EFD= ADC.
(2)(1)中结论仍成立.
理由:AD平分BAG,
BAD= GAD.
FAE=GAD,
FAE=BAD.
又AEB= ABC,
AEB-FAE=ABC-BAD,
即EFD= ADC.
第2页,共2页
学校:___________姓名:___________班级:___________考号:___________
一、选择题(本大题共12小题,共36分)
如图,在ABC中,A=,B=,则C的度数是( )
A. B. C. D.
如图,在ABC中,A=,B=,DEBC,则AED的度数是( )
A. B. C. D.
如图,ABCD,且DEC=,C=,则B的度数是( )
A. B. C. D.
如图,在ABC中,AB=AC,A=,BD是AC边上的高,则DBC的度数是( )
A.
B.
C.
D.
一副学生用的三角板按如图所示的方式放置,则AOD的度数为( )
A. B. C. D.
如图,在ABC中,AB=AC,BAC=,AB的垂直平分线DE分别交AB,BC于点D,E,则BAE的度数是( )
A. B. C. D.
如图,在ABC中,AD是BC边上的高,BE平分ABC交AC于点E,BAC=,ABE=,则DAC的度数是( )
A. B. C. D.
下列命题正确的是( )
A. 三角形的一个外角等于该三角形的两个内角之和
B. 三角形的一个外角大于任何一个内角
C. 三角形的一个外角等于和它不相邻的两个内角之和
D. 三角形的任意两个外角都不可能相等
如图,ACD是ABC的外角,CE平分ACD.若A=,B=,则ECD的度数为( )
A. B. C. D.
如图,ABCD,B=,E=,则D的度数为( )
A. B. C. D.
如图,在ABC中,AB=AC,A=,点E在BC边的延长线上,ABC与ACE的平分线相交于点D,则D等于( )
A. B.
C. D.
如图,点D在BC的延长线上,DEAB于点E,交AC于点F.若A=,D=,则ACB的度数为( )
A. B. C. D.
二、填空题(本大题共8小题,共24分)
如图,ABCD,AE交CD于点C,DEAE于点E.若A=,则D= .
如图所示,已知点P是ABC、ACB的平分线的交点,若A=,则BPC= 度.
如图是A,B,C三岛的平面图,C岛在A岛的北偏东方向上,B岛在A岛的北偏东方向上,C岛在B岛的北偏东方向上,则ACB= .
如图,在ABC中,BO,CO分别平分ABC,ACB.若BOC=,则A= .
如图,已知AOD=,点C是射线OD上的一个动点.在点C的运动过程中,AOC恰好是直角三角形,则此时A所有可能的度数为 .
若O是△ABC外一点,OB、OC分别平分△ABC的外角∠CBE、∠BCF,若∠A=50°,则∠BOC=______度.
(1)如图1,P是ABC中BC边的延长线上一点,A=,B=,则ACP= .
(2)如图2,ACD是ABC的外角.若ACD=,B=,则A= .
(3)如图3,若3=,则1-2= .
如图,A+B+C+D+E= .
三、解答题(本大题共5小题,共40分)
如图,已知ABCD,BEF和EFD的平分线相交于点G.求证:EGFG.
如图,在中,AD⊥BC于点D,AE平分∠BAC,
(1)若∠B-∠C=30°,求∠DAE的度数.
(2)若B-C=(B>C),求DAE的度数.(用含的代数式表示)
如图1,线段AB,CD相交于点O,连接AD,CB,我们把形如图1的图形称之为“8字形”.如图2,在图1的条件下,DAB和BCD的平分线AP和CP相交于点P,且与CD,AB分别相交于点M,N.
(1)直接写出图1中A,B,C,D之间的数量关系: .
(2)在图2中,若D=,B=,试求P的度数.
(3)当图2中D和B为任意角时,其他条件不变,P与D,B之间存在着怎样的数量关系 (直接写出结论即可)
一个零件的形状如图所示,规定:A=,B=,C=.李叔叔量得BDC=,判定这个零件不合格,你能说出其中的道理吗
如图,在ABC中,点E在AC上,AEB=ABC.
(1)图1中,作BAC的平分线AD,分别交CB, BE于D,F两点.求证:EFD=ADC.
(2)图2中,作ABC的外角BAG的平分线AD,分别交CB,BE的延长线于D,F两点.试探究(1)中结论是否仍成立,为什么
1.【答案】B
2.【答案】D
3.【答案】B
4.【答案】A
5.【答案】C
6.【答案】D
7.【答案】B
8.【答案】C
9.【答案】C
10.【答案】B
11.【答案】A
12.【答案】B
13.【答案】
14.【答案】130
15.【答案】
16.【答案】
17.【答案】或
18.【答案】65
19.【答案】
20.【答案】
21.【答案】证明:ABCD,
BEF+EFD=.
BEF和EFD的平分线交于点G,
FEG=BEF,EFG=EFD.
FEG+EFG=(BEF+EFD)=.
FEG+EFG+G=,
G=.
EGFG.
22.【答案】解:(1)ADBC,
ADC=.
AE平分BAC,
EAC=BAC.
而BAC=-B-C,
EAC=-B-C.
DAC=-C,
DAE=DAC-EAC=-C-(-B-C)= (B-C)=.
(2)ADBC,
ADC=.
AE平分BAC,
EAC=BAC.
又BAC=-B-C,
EAC=-B-C.
DAC=-C,
DAE= DAC-EAC=-C-(-B-C)= (B-C).
B-C=(B>C),
DAE=.
23.【答案】解:(1)A+D=C+B
(2)D+1+2=B+3+4,1=2,3=4,
+22=+24.
4-2=
B+4=P+2,
P=B+4-2=+=.
(3)P=.
24.【答案】解:连接AD并延长至点E,
BDE=B+BAD,CDE= C+CAD.
BAC=,B=,C=,
BDC= BDE+CDE=B+BAD+CAD+C=B+BAC+ C=++=.
,
这个零件不合格.
25.【答案】解:(1)证明:AD平分BAC,
BAD=DAC.
又AEB= ABC,
DAC+AEB=ABC+BAD,
即EFD= ADC.
(2)(1)中结论仍成立.
理由:AD平分BAG,
BAD= GAD.
FAE=GAD,
FAE=BAD.
又AEB= ABC,
AEB-FAE=ABC-BAD,
即EFD= ADC.
第2页,共2页
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
