2021-2022学年京改版七年级上册数学第2章 一元一次方程单元测试卷(Word版含答案)
文档属性
| 名称 | 2021-2022学年京改版七年级上册数学第2章 一元一次方程单元测试卷(Word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 166.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北京课改版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 18:12:40 | ||
图片预览




文档简介
2021-2022学年北京课改新版七年级上册数学《第2章 一元一次方程》单元测试卷
一.选择题
1.下列用语言叙述式子:﹣4表示的数量关系,表述不正确的是( )
A.比x的倒数小4的数 B.比x的倒数大4的数
C.x的倒数与4的差 D.1除以x的商与4的差
2.下列四个叙述,哪一个是正确的( )
A.3x表示3+x B.x2表示x+x
C.3x2表示3x 3x D.3x+5表示x+x+x+5
3.当x=2时,ax+3的值是5;当x=﹣2时,代数式ax﹣3的值是( )
A.﹣5 B.1 C.﹣1 D.2
4.下列各组式子中是同类项的是( )
A.4x与4y B.4xy2与4xy C.4xy2与4x2y D.4xy2与4y2x
5.下列合并同类项正确的是( )
A.3+2ab=5ab B.5xy﹣x=5y
C.﹣5mn2+5n2m=0 D.a3﹣a=a2
6.下列代数式的书写格式规范的是( )
A. B.a×b÷5+1 C.ab2 D.
7.用代数式表示“a的2倍与b的和的平方”,正确的是( )
A.(2a+b)2 B.2(a+b)2 C.2a+b2 D.(a+2b)2
8.下列各组的两项是同类项的是( )
A.3m2n2与3m3n2 B.2xy与yx
C.53与a3 D.3x2y2与4x2z2
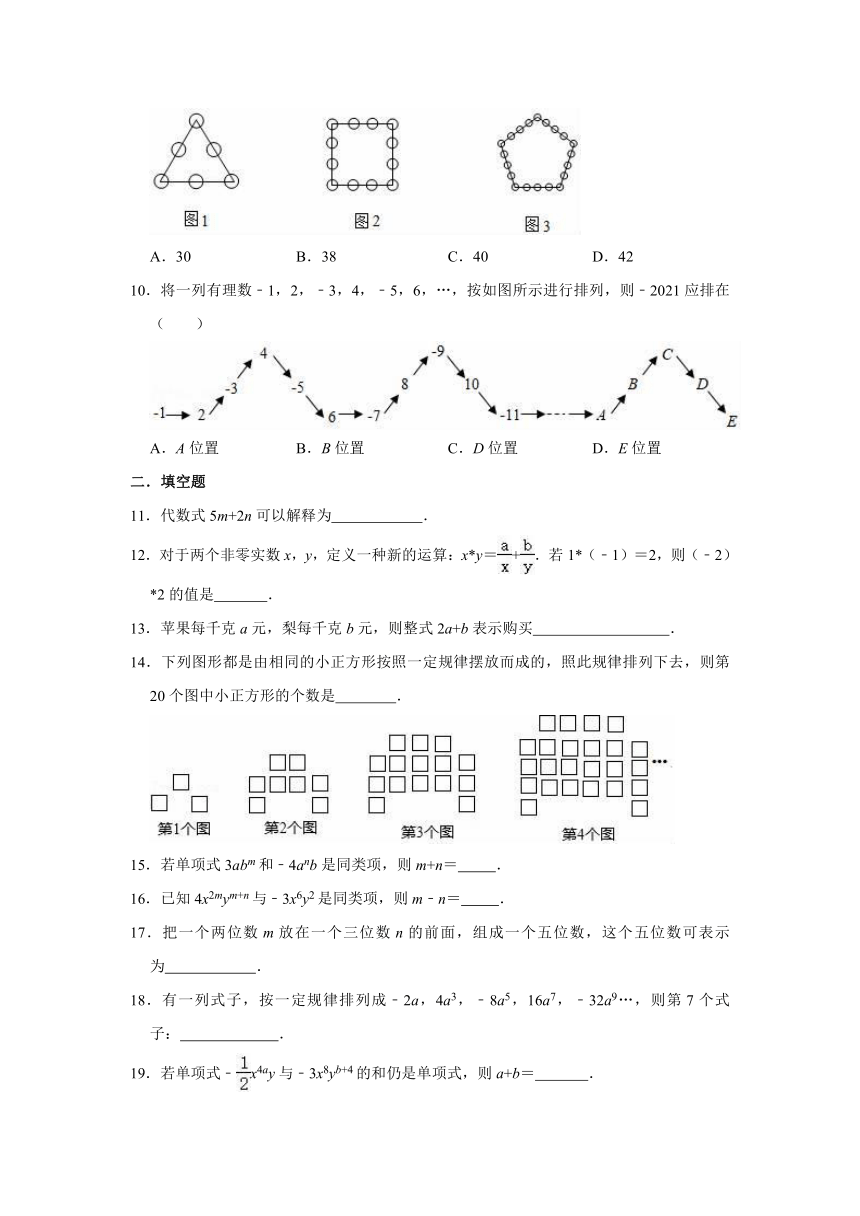
9.如图所示,第一个图形共6个小圆圈,第二个图形共12个小圆圈,第三个图形共20个小圆圈,则按此规律,第五个图形共( )个小圆圈.
A.30 B.38 C.40 D.42
10.将一列有理数﹣1,2,﹣3,4,﹣5,6,…,按如图所示进行排列,则﹣2021应排在( )
A.A位置 B.B位置 C.D位置 D.E位置
二.填空题
11.代数式5m+2n可以解释为 .
12.对于两个非零实数x,y,定义一种新的运算:x*y=+.若1*(﹣1)=2,则(﹣2)*2的值是 .
13.苹果每千克a元,梨每千克b元,则整式2a+b表示购买 .
14.下列图形都是由相同的小正方形按照一定规律摆放而成的,照此规律排列下去,则第20个图中小正方形的个数是 .
15.若单项式3abm和﹣4anb是同类项,则m+n= .
16.已知4x2mym+n与﹣3x6y2是同类项,则m﹣n= .
17.把一个两位数m放在一个三位数n的前面,组成一个五位数,这个五位数可表示为 .
18.有一列式子,按一定规律排列成﹣2a,4a3,﹣8a5,16a7,﹣32a9…,则第7个式子: .
19.若单项式﹣x4ay与﹣3x8yb+4的和仍是单项式,则a+b= .
20.当x=2时,代数式ax3﹣bx+1的值等于﹣17,那么当x=﹣1时,代数式﹣3bx3+12ax﹣5的值 .
三.解答题
21.数学中,运用整体思想方法在求代数式的值中非常重要.
例如:已知,a2+2a=1,则代数式2a2+4a+4=2(a2+2a)+4=2×1+4=6.
请你根据以上材料解答以下问题:
(1)若x2﹣3x=2,则1+3x﹣x2= ;
(2)已知a﹣b=5,b﹣c=3,求代数式(a﹣c)2﹣3a+2+3c的值;
(3)当x=﹣1,y=2时,代数式ax2y﹣bxy2﹣1的值为8,则当x=1,y=﹣2时,求代数式ax2y﹣bxy2﹣1的值.
22.请你结合自身生活实际,设计具体情境,解释下列代数式的意义:
①(1﹣20%)x;
②a3;
③;
④.
23.关于x的代数式ax2+bx+c,若b2﹣4ac>0,则称代数式为完美代数式.
已知关于x的代数式:①x2﹣4x+m﹣1;②x2+(m+1)x﹣m﹣3.
(1)若代数式①是完美代数式,求m的取值范围;
(2)判断代数式②是否为完美代数式.
24.某商场将进货价为35元台灯以50元销售价售出,平均每月能售出500个,市场调研表明:当销售价每上涨1元时,其销售量就将减少10个.若设每个台灯的销售价上涨a元.
(1)试用含a的代数式填空:涨价后,每个台灯的销售价为 元,利润为 元,商场的台灯平均每月的销售量为 台.
(2)如果商场要想销售利润平均每月达到10000,商场经理甲说:“在原售价每台50元的基础上再上涨25元,可以完成任务”,商场经理乙说:“不用涨那么多,在原售价每台50元的基础上再上涨15元就可以了”,为减少库存,应该采取谁的意见?
25.绝对值拓展材料:|a|表示数a在数轴上的对应点与原点的距离.如:|5|表示5在数轴上的对应点到原点的距离,而|5|=|5﹣0|,即|5﹣0|表示5、0在数轴上对应的两点之间的距离,类似的,有:|5+3|=|5﹣(﹣3)|表示5、﹣3在数轴上对应的两点之间的距离.一般地,点A、B在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为|a﹣b|.
完成下列题目:
(1)A、B分别为数轴上两点,A点对应的数为﹣2,B点对应的数为4:
①A、B两点之间的距离为 (写计算结果);
②折叠数轴,使A点与B点重合,则表示﹣3的点与表示 的点重合;
③若在数轴上存在一点P到A的距离是点P到B的距离的2倍,则点P所表示的数是 ;
④如果数轴上表示数a的点位于﹣2和4之间,那么|a+2|+|a﹣4|= .
(2)求|x﹣2|+|x+2|的最小值为 ,若满足|x﹣2|+|x+2|=6时,则x的值是 .
26.观察下面三行数:
﹣2,4,﹣8,16,﹣32,64 …①
0,6,﹣6,18,﹣30,66…②
﹣1,2,﹣4,8,﹣16,32…③
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数有什么关系?
(3)取每行数的第十个数,计算这三个数的和.
27.图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为1+2+3+…+n=.
如果图3中的圆圈共有13层.
(1)我们自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层最左边这个圆圈中的数是 ;
(2)我们自上往下,在每个圆圈中按图4的方式填上一串连续的整数﹣23,﹣22,﹣21,﹣20,…,求最底层最右边圆圈内的数是 ;
(3)求图4中所有圆圈中各数值之和.(写出计算过程)
参考答案与试题解析
一.选择题
1.解:A选项表示的是﹣4;
B选项表示的是+4;
C选项表示的是﹣4;
D选项表示﹣4.
故选:B.
2.解:A、3x=3 x,
B、x2=x x,
C、3x2=3x x,
D、3x+5=x+x+x+5.
故选:D.
3.解:根据题意得2a+3=5,
解得:a=1,
把a=1以及x=﹣2代入,
得:ax﹣3=﹣2﹣3=﹣5.
故选:A.
4.解:A、4x与4y字母不同,不是同类项;
B、4xy2与4xy字母相同但字母的指数不同,不是同类项;
C、4xy2与4x2y字母相同但字母的指数不同,不是同类项;
D、4xy2与4y2x字母相同,字母的指数相同,是同类项.故选D.
5.解:A、不是同类项,不能合并;
B、不是同类项,不能合并;
C、符合同类项的定义;
D、不是同类项,不能合并.
故选:C.
6.解:A、1xyz书写不规范,应写为xyz,故此选项不符合题意;
B、a×b÷5+1书写不规范,应写为+1,故此选项不符合题意;
C、ab2书写不规范,应写为2ab,故此选项不符合题意;
D、ab书写规范,故此选项符合题意;
故选:D.
7.解:a的2倍为2a,与b的和为(2a+b),则“a的2倍与b的和的平方”表示为(2a+b)2,
故选:A.
8.解:A、m的次数不同,故不是同类项,选项错误;
B、是同类项,选项正确;
C、所含字母不同,不是同类项,选项错误;
D、所含字母不同,不是同类项,选项错误.
故选:B.
9.解:第1个图的小圆圈的个数为:6=2×3=(1+1)×(1+2),
第2个图的小圆圈的个数为:12=3×4=(1+2)×(2+2),
第3个图的小圆圈的个数为:20=4×5=(1+3)×(3+2),
...
则第n个图的小圆圈的个数为:(1+n)(n+2),
∴第5个图形的小圆圈的个数为:(1+5)(5+2)=6×7=42.
故选:D.
10.解:由图可知,
每个凸起对应5个数字,这些数字的奇数都是负数,偶数都是正数,
∵(2021﹣1)÷5=2020÷5=404,
∴﹣2021应排在E位置,
故选:D.
二.填空题
11.解:可以解释为5m与2n的和,也可以是一个数的5倍与另一个数的2倍的和.
答案不唯一,只要列出的代数式是5m+2n即可.
12.解:∵1*(﹣1)=2,
∴=2
即a﹣b=2
∴原式==(a﹣b)=﹣1
故答案为:﹣1
13.解:∵苹果每千克a元,∴2a表示2千克苹果的钱数,
则整式2a+b表示购买2千克苹果和1千克梨的钱数,
故答案为:2千克苹果和1千克梨的钱数.
14.解:第1个图中正方形的个数为1×3=3;
第2个图中正方形的个数为2×4=8;
第3个图中正方形的个数为3×5=15;
第4个图中正方形的个数为4×6=24;
…
发现规律:
第n个图中正方形的个数为n(n+2);
∴:第20个图中正方形的个数为20×22=440.
故答案为440.
15.解:根据题意可得:m=1,n=1,
把m=1,n=1代入m+n=2,
故答案为:2
16.解:根据题意得:,
解得:,
则m﹣n=3+1=4.
故答案是:4.
17.解:∵五位数是两位数m乘以1000,后边的三位数是n,
∴组成的五位数为1000m+n.
例如:23456=23×1000+456.
故答案为1000m+n.
18.解:∵第1个式子﹣2a=(﹣2)1 a2×1﹣1,
第2个式子4a3=(﹣2)2 a2×2﹣1,
第3个式子﹣8a5=(﹣2)3 a2×3﹣1,
……
∴第n个式子为(﹣2)n a2n﹣1,
则第7个式子为(﹣2)7 a2×7﹣1=﹣128a13,
故答案为:﹣128a13.
19.解:由题意,得
4a=8,b+4=1.
借的a=2,b=﹣3.
a+b=﹣3+2=﹣1,
故答案为:﹣1.
20.解:x=2时,ax3﹣bx+1=a 23﹣b 2+1=8a﹣2b+1,
∴8a﹣2b+1=﹣17,
∴8a﹣2b=﹣18,
∴4a﹣b=﹣9.
当x=﹣1时,﹣3bx3+12ax﹣5=12a×(﹣1)﹣3b×(﹣1)3﹣5,
=﹣12a+3b﹣5
=﹣3(4a﹣b)﹣5
=﹣3×(﹣9)﹣5
=27﹣5
=22.
故答案为:22.
三.解答题
21.解:(1)因为x2﹣3x=2,
所以1+3x﹣x2=1﹣(x2﹣3x)
=1﹣2=﹣1
故答案为:﹣1.
(2)∵a﹣b=5,b﹣c=3,
∴a﹣b+b﹣c=a﹣c=5+3=8,
∴(a﹣c)2﹣3a+2+3c=(a﹣c)2﹣3(a﹣c)+2=(a﹣c﹣2) (a﹣c﹣1)=(8﹣2)×(8﹣1)=42;
(3)∵当x=﹣1,y=2时,代数式ax2y﹣bxy2﹣1的值为8,
即2a+4b﹣1=8,
可得2a+4b=9,
∴当x=1,y=﹣2时,代数式ax2y﹣bxy2﹣1=﹣2a﹣4b﹣1=﹣(2a+4b)﹣1=﹣9﹣1=﹣10.
22.解:①小明家二月份用电量x度,三月份减少20%,则三月份用电量为(1﹣20%)x度;
②a表示立方体的棱长,则a3表示该立方体的体积;
③汽车每小时行驶m千米,行驶30千米所用时间为小时;
④骑车上坡每分钟走a米,下坡每分钟走b米,那么上坡3分钟和下坡2分钟后的平均每分钟走多少米.
23.解:(1)∵代数式①是完美代数式,
∴(﹣4)2﹣4(m﹣1)>0,
解得m<5.
故m的取值范围是m<5;
(2)∵(m+1)2﹣4(﹣m﹣3)=(m+3)2+4,
∵(m+3)2≥0,
∴(m+3)2+4>0
∴代数式②是完美代数式.
24.解:(1)涨价后,每个台灯的销售价为(50+a)元;
涨价后,商场的台灯平均每月的销售量为(500﹣10a)台;
涨价后,商场每月销售台灯所获得总利润为(15+a)(500﹣10a)元.
故答案是:(50+a);(15+a);(500﹣10a);
(2)经理甲:当a=25时,(15+25)(500﹣10×25)=10000(元).
经理乙:当a=15时,(15+15)(500﹣10×15)=10500(元).
因为为减少库存,所以应该采取经理乙的意见.
25.解:(1)①A、B两点之间的距离为4﹣(﹣2)=6,
故答案为:6;
②折叠数轴,使A点与B点重合,则折痕为点1,则表示﹣3的点与表示5的点重合;
故答案为:5;
③分两种情况:
当P在AB之间时,P表示的数为2,
当P在B的右侧时,P表示的数为10,
综上,则点P所表示的数是2或10;
故答案为:2或10;
④如果数轴上表示a的点在﹣2和4之间,
那么|a+2|表示a到﹣2的距离,|α﹣4|表示a到4的距离,因为a在﹣2和4之间,
故|a+2|+|a﹣4|=4﹣(﹣2)=6.
故答案为:6.
(2)|x﹣2|表示x与2距离,所以当表示x的点在2与﹣2之间时,|x﹣2|+|x+2|的值最小,且最小值是4,
|x﹣2|+|x+2|=6,
∴当x<﹣2时,2﹣x﹣x﹣2=6,得x=﹣3,
当﹣2≤x≤2时,2﹣x+x+2=4≠6,故此时无解;
当x>2时,x﹣2+x+2=6,得x=3,
故答案为:4,±3.
26.解:(1)(﹣2)n;
(2)第②③行数与第①行数的关系为:第②行数比第①行相对应的数大2;第③行数是第①行相对应的数的;
(3)第一行的第十个数为:1024;
第二行的第十个数为:1026;
第三行的第十个数为:512;
1024+1026+512=2562.
故这三个数的和为:2562.
27.解:(1)当有13层时,图3中到第12层共有:1+2+3+…+11+12=78个圆圈,
最底层最左边这个圆圈中的数是:78+1=79;
(2)图4中所有圆圈中共有1+2+3+…+13==91个数,
最底层最右边圆圈内的数是﹣23+91﹣1=67;
(3)图4中共有91个数,其中23个负数,1个0,67个正数,
所以图4中所有圆圈中各数的和为:
﹣23﹣22﹣…﹣1+0+1+2+…+67
=﹣(1+2+3+…+23)+(1+2+3+…+67)
=﹣276+2278
=2002.
故答案为:(1)79;(2)67.
一.选择题
1.下列用语言叙述式子:﹣4表示的数量关系,表述不正确的是( )
A.比x的倒数小4的数 B.比x的倒数大4的数
C.x的倒数与4的差 D.1除以x的商与4的差
2.下列四个叙述,哪一个是正确的( )
A.3x表示3+x B.x2表示x+x
C.3x2表示3x 3x D.3x+5表示x+x+x+5
3.当x=2时,ax+3的值是5;当x=﹣2时,代数式ax﹣3的值是( )
A.﹣5 B.1 C.﹣1 D.2
4.下列各组式子中是同类项的是( )
A.4x与4y B.4xy2与4xy C.4xy2与4x2y D.4xy2与4y2x
5.下列合并同类项正确的是( )
A.3+2ab=5ab B.5xy﹣x=5y
C.﹣5mn2+5n2m=0 D.a3﹣a=a2
6.下列代数式的书写格式规范的是( )
A. B.a×b÷5+1 C.ab2 D.
7.用代数式表示“a的2倍与b的和的平方”,正确的是( )
A.(2a+b)2 B.2(a+b)2 C.2a+b2 D.(a+2b)2
8.下列各组的两项是同类项的是( )
A.3m2n2与3m3n2 B.2xy与yx
C.53与a3 D.3x2y2与4x2z2
9.如图所示,第一个图形共6个小圆圈,第二个图形共12个小圆圈,第三个图形共20个小圆圈,则按此规律,第五个图形共( )个小圆圈.
A.30 B.38 C.40 D.42
10.将一列有理数﹣1,2,﹣3,4,﹣5,6,…,按如图所示进行排列,则﹣2021应排在( )
A.A位置 B.B位置 C.D位置 D.E位置
二.填空题
11.代数式5m+2n可以解释为 .
12.对于两个非零实数x,y,定义一种新的运算:x*y=+.若1*(﹣1)=2,则(﹣2)*2的值是 .
13.苹果每千克a元,梨每千克b元,则整式2a+b表示购买 .
14.下列图形都是由相同的小正方形按照一定规律摆放而成的,照此规律排列下去,则第20个图中小正方形的个数是 .
15.若单项式3abm和﹣4anb是同类项,则m+n= .
16.已知4x2mym+n与﹣3x6y2是同类项,则m﹣n= .
17.把一个两位数m放在一个三位数n的前面,组成一个五位数,这个五位数可表示为 .
18.有一列式子,按一定规律排列成﹣2a,4a3,﹣8a5,16a7,﹣32a9…,则第7个式子: .
19.若单项式﹣x4ay与﹣3x8yb+4的和仍是单项式,则a+b= .
20.当x=2时,代数式ax3﹣bx+1的值等于﹣17,那么当x=﹣1时,代数式﹣3bx3+12ax﹣5的值 .
三.解答题
21.数学中,运用整体思想方法在求代数式的值中非常重要.
例如:已知,a2+2a=1,则代数式2a2+4a+4=2(a2+2a)+4=2×1+4=6.
请你根据以上材料解答以下问题:
(1)若x2﹣3x=2,则1+3x﹣x2= ;
(2)已知a﹣b=5,b﹣c=3,求代数式(a﹣c)2﹣3a+2+3c的值;
(3)当x=﹣1,y=2时,代数式ax2y﹣bxy2﹣1的值为8,则当x=1,y=﹣2时,求代数式ax2y﹣bxy2﹣1的值.
22.请你结合自身生活实际,设计具体情境,解释下列代数式的意义:
①(1﹣20%)x;
②a3;
③;
④.
23.关于x的代数式ax2+bx+c,若b2﹣4ac>0,则称代数式为完美代数式.
已知关于x的代数式:①x2﹣4x+m﹣1;②x2+(m+1)x﹣m﹣3.
(1)若代数式①是完美代数式,求m的取值范围;
(2)判断代数式②是否为完美代数式.
24.某商场将进货价为35元台灯以50元销售价售出,平均每月能售出500个,市场调研表明:当销售价每上涨1元时,其销售量就将减少10个.若设每个台灯的销售价上涨a元.
(1)试用含a的代数式填空:涨价后,每个台灯的销售价为 元,利润为 元,商场的台灯平均每月的销售量为 台.
(2)如果商场要想销售利润平均每月达到10000,商场经理甲说:“在原售价每台50元的基础上再上涨25元,可以完成任务”,商场经理乙说:“不用涨那么多,在原售价每台50元的基础上再上涨15元就可以了”,为减少库存,应该采取谁的意见?
25.绝对值拓展材料:|a|表示数a在数轴上的对应点与原点的距离.如:|5|表示5在数轴上的对应点到原点的距离,而|5|=|5﹣0|,即|5﹣0|表示5、0在数轴上对应的两点之间的距离,类似的,有:|5+3|=|5﹣(﹣3)|表示5、﹣3在数轴上对应的两点之间的距离.一般地,点A、B在数轴上分别表示有理数a、b,那么A、B之间的距离可表示为|a﹣b|.
完成下列题目:
(1)A、B分别为数轴上两点,A点对应的数为﹣2,B点对应的数为4:
①A、B两点之间的距离为 (写计算结果);
②折叠数轴,使A点与B点重合,则表示﹣3的点与表示 的点重合;
③若在数轴上存在一点P到A的距离是点P到B的距离的2倍,则点P所表示的数是 ;
④如果数轴上表示数a的点位于﹣2和4之间,那么|a+2|+|a﹣4|= .
(2)求|x﹣2|+|x+2|的最小值为 ,若满足|x﹣2|+|x+2|=6时,则x的值是 .
26.观察下面三行数:
﹣2,4,﹣8,16,﹣32,64 …①
0,6,﹣6,18,﹣30,66…②
﹣1,2,﹣4,8,﹣16,32…③
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数有什么关系?
(3)取每行数的第十个数,计算这三个数的和.
27.图1是由若干个小圆圈堆成的一个形如等边三角形的图案,最上面一层有一个圆圈,以下各层均比上一层多一个圆圈,一共堆了n层.将图1倒置后与原图1拼成图2的形状,这样我们可以算出图1中所有圆圈的个数为1+2+3+…+n=.
如果图3中的圆圈共有13层.
(1)我们自上往下,在每个圆圈中按图3的方式填上一串连续的正整数1,2,3,4,…,则最底层最左边这个圆圈中的数是 ;
(2)我们自上往下,在每个圆圈中按图4的方式填上一串连续的整数﹣23,﹣22,﹣21,﹣20,…,求最底层最右边圆圈内的数是 ;
(3)求图4中所有圆圈中各数值之和.(写出计算过程)
参考答案与试题解析
一.选择题
1.解:A选项表示的是﹣4;
B选项表示的是+4;
C选项表示的是﹣4;
D选项表示﹣4.
故选:B.
2.解:A、3x=3 x,
B、x2=x x,
C、3x2=3x x,
D、3x+5=x+x+x+5.
故选:D.
3.解:根据题意得2a+3=5,
解得:a=1,
把a=1以及x=﹣2代入,
得:ax﹣3=﹣2﹣3=﹣5.
故选:A.
4.解:A、4x与4y字母不同,不是同类项;
B、4xy2与4xy字母相同但字母的指数不同,不是同类项;
C、4xy2与4x2y字母相同但字母的指数不同,不是同类项;
D、4xy2与4y2x字母相同,字母的指数相同,是同类项.故选D.
5.解:A、不是同类项,不能合并;
B、不是同类项,不能合并;
C、符合同类项的定义;
D、不是同类项,不能合并.
故选:C.
6.解:A、1xyz书写不规范,应写为xyz,故此选项不符合题意;
B、a×b÷5+1书写不规范,应写为+1,故此选项不符合题意;
C、ab2书写不规范,应写为2ab,故此选项不符合题意;
D、ab书写规范,故此选项符合题意;
故选:D.
7.解:a的2倍为2a,与b的和为(2a+b),则“a的2倍与b的和的平方”表示为(2a+b)2,
故选:A.
8.解:A、m的次数不同,故不是同类项,选项错误;
B、是同类项,选项正确;
C、所含字母不同,不是同类项,选项错误;
D、所含字母不同,不是同类项,选项错误.
故选:B.
9.解:第1个图的小圆圈的个数为:6=2×3=(1+1)×(1+2),
第2个图的小圆圈的个数为:12=3×4=(1+2)×(2+2),
第3个图的小圆圈的个数为:20=4×5=(1+3)×(3+2),
...
则第n个图的小圆圈的个数为:(1+n)(n+2),
∴第5个图形的小圆圈的个数为:(1+5)(5+2)=6×7=42.
故选:D.
10.解:由图可知,
每个凸起对应5个数字,这些数字的奇数都是负数,偶数都是正数,
∵(2021﹣1)÷5=2020÷5=404,
∴﹣2021应排在E位置,
故选:D.
二.填空题
11.解:可以解释为5m与2n的和,也可以是一个数的5倍与另一个数的2倍的和.
答案不唯一,只要列出的代数式是5m+2n即可.
12.解:∵1*(﹣1)=2,
∴=2
即a﹣b=2
∴原式==(a﹣b)=﹣1
故答案为:﹣1
13.解:∵苹果每千克a元,∴2a表示2千克苹果的钱数,
则整式2a+b表示购买2千克苹果和1千克梨的钱数,
故答案为:2千克苹果和1千克梨的钱数.
14.解:第1个图中正方形的个数为1×3=3;
第2个图中正方形的个数为2×4=8;
第3个图中正方形的个数为3×5=15;
第4个图中正方形的个数为4×6=24;
…
发现规律:
第n个图中正方形的个数为n(n+2);
∴:第20个图中正方形的个数为20×22=440.
故答案为440.
15.解:根据题意可得:m=1,n=1,
把m=1,n=1代入m+n=2,
故答案为:2
16.解:根据题意得:,
解得:,
则m﹣n=3+1=4.
故答案是:4.
17.解:∵五位数是两位数m乘以1000,后边的三位数是n,
∴组成的五位数为1000m+n.
例如:23456=23×1000+456.
故答案为1000m+n.
18.解:∵第1个式子﹣2a=(﹣2)1 a2×1﹣1,
第2个式子4a3=(﹣2)2 a2×2﹣1,
第3个式子﹣8a5=(﹣2)3 a2×3﹣1,
……
∴第n个式子为(﹣2)n a2n﹣1,
则第7个式子为(﹣2)7 a2×7﹣1=﹣128a13,
故答案为:﹣128a13.
19.解:由题意,得
4a=8,b+4=1.
借的a=2,b=﹣3.
a+b=﹣3+2=﹣1,
故答案为:﹣1.
20.解:x=2时,ax3﹣bx+1=a 23﹣b 2+1=8a﹣2b+1,
∴8a﹣2b+1=﹣17,
∴8a﹣2b=﹣18,
∴4a﹣b=﹣9.
当x=﹣1时,﹣3bx3+12ax﹣5=12a×(﹣1)﹣3b×(﹣1)3﹣5,
=﹣12a+3b﹣5
=﹣3(4a﹣b)﹣5
=﹣3×(﹣9)﹣5
=27﹣5
=22.
故答案为:22.
三.解答题
21.解:(1)因为x2﹣3x=2,
所以1+3x﹣x2=1﹣(x2﹣3x)
=1﹣2=﹣1
故答案为:﹣1.
(2)∵a﹣b=5,b﹣c=3,
∴a﹣b+b﹣c=a﹣c=5+3=8,
∴(a﹣c)2﹣3a+2+3c=(a﹣c)2﹣3(a﹣c)+2=(a﹣c﹣2) (a﹣c﹣1)=(8﹣2)×(8﹣1)=42;
(3)∵当x=﹣1,y=2时,代数式ax2y﹣bxy2﹣1的值为8,
即2a+4b﹣1=8,
可得2a+4b=9,
∴当x=1,y=﹣2时,代数式ax2y﹣bxy2﹣1=﹣2a﹣4b﹣1=﹣(2a+4b)﹣1=﹣9﹣1=﹣10.
22.解:①小明家二月份用电量x度,三月份减少20%,则三月份用电量为(1﹣20%)x度;
②a表示立方体的棱长,则a3表示该立方体的体积;
③汽车每小时行驶m千米,行驶30千米所用时间为小时;
④骑车上坡每分钟走a米,下坡每分钟走b米,那么上坡3分钟和下坡2分钟后的平均每分钟走多少米.
23.解:(1)∵代数式①是完美代数式,
∴(﹣4)2﹣4(m﹣1)>0,
解得m<5.
故m的取值范围是m<5;
(2)∵(m+1)2﹣4(﹣m﹣3)=(m+3)2+4,
∵(m+3)2≥0,
∴(m+3)2+4>0
∴代数式②是完美代数式.
24.解:(1)涨价后,每个台灯的销售价为(50+a)元;
涨价后,商场的台灯平均每月的销售量为(500﹣10a)台;
涨价后,商场每月销售台灯所获得总利润为(15+a)(500﹣10a)元.
故答案是:(50+a);(15+a);(500﹣10a);
(2)经理甲:当a=25时,(15+25)(500﹣10×25)=10000(元).
经理乙:当a=15时,(15+15)(500﹣10×15)=10500(元).
因为为减少库存,所以应该采取经理乙的意见.
25.解:(1)①A、B两点之间的距离为4﹣(﹣2)=6,
故答案为:6;
②折叠数轴,使A点与B点重合,则折痕为点1,则表示﹣3的点与表示5的点重合;
故答案为:5;
③分两种情况:
当P在AB之间时,P表示的数为2,
当P在B的右侧时,P表示的数为10,
综上,则点P所表示的数是2或10;
故答案为:2或10;
④如果数轴上表示a的点在﹣2和4之间,
那么|a+2|表示a到﹣2的距离,|α﹣4|表示a到4的距离,因为a在﹣2和4之间,
故|a+2|+|a﹣4|=4﹣(﹣2)=6.
故答案为:6.
(2)|x﹣2|表示x与2距离,所以当表示x的点在2与﹣2之间时,|x﹣2|+|x+2|的值最小,且最小值是4,
|x﹣2|+|x+2|=6,
∴当x<﹣2时,2﹣x﹣x﹣2=6,得x=﹣3,
当﹣2≤x≤2时,2﹣x+x+2=4≠6,故此时无解;
当x>2时,x﹣2+x+2=6,得x=3,
故答案为:4,±3.
26.解:(1)(﹣2)n;
(2)第②③行数与第①行数的关系为:第②行数比第①行相对应的数大2;第③行数是第①行相对应的数的;
(3)第一行的第十个数为:1024;
第二行的第十个数为:1026;
第三行的第十个数为:512;
1024+1026+512=2562.
故这三个数的和为:2562.
27.解:(1)当有13层时,图3中到第12层共有:1+2+3+…+11+12=78个圆圈,
最底层最左边这个圆圈中的数是:78+1=79;
(2)图4中所有圆圈中共有1+2+3+…+13==91个数,
最底层最右边圆圈内的数是﹣23+91﹣1=67;
(3)图4中共有91个数,其中23个负数,1个0,67个正数,
所以图4中所有圆圈中各数的和为:
﹣23﹣22﹣…﹣1+0+1+2+…+67
=﹣(1+2+3+…+23)+(1+2+3+…+67)
=﹣276+2278
=2002.
故答案为:(1)79;(2)67.
同课章节目录
- 第一章 有理数
- 1.1 负数的引入
- 1.2 用数轴上的点表示有理数
- 1.3 相反数和绝对值
- 1.4 有理数的加法
- 1.5 有理数的减法
- 1.6 有理数加减法的混合运算
- 1.7 有理数的乘法
- 1.8 有理数的除法
- 1.9 有理数的乘方
- 1.10 有理数的混合运算
- 1.11 数的近似和科学记数法
- 1.12 用计算器做有理数的混合运算
- 第二章 一元一次方程
- 2.1 字母表示数
- 2.2 同类项与合并同类项
- 2.3 等式与方程
- 2.4 等式的基本性质
- 2.5 一元一次方程
- 2.6 列方程解应用问题
- 第三章 简单的几何图形
- 3.1 平面图形与立体图形
- 3.2 某些立体图形的展开图
- 3.3 从不同方向观察立体图形
- 3.4 点、线、面、体
- 3.5 直线、射线、线段
- 3.6 角及其分类
- 3.7 角的度量与角的换算
- 3.8 角平分线
- 3.9 两条直线的位置关系
- 3.10 相交线与平行线
- 3.11 用计算机绘图
