人教版八年级上册数学12.2全等三角形的判定和性质证明题训练卷(word版,含答案)
文档属性
| 名称 | 人教版八年级上册数学12.2全等三角形的判定和性质证明题训练卷(word版,含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 722.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 09:28:55 | ||
图片预览


文档简介
人教版八年级上册数学12.2全等三角形的判定和性质证明题训练
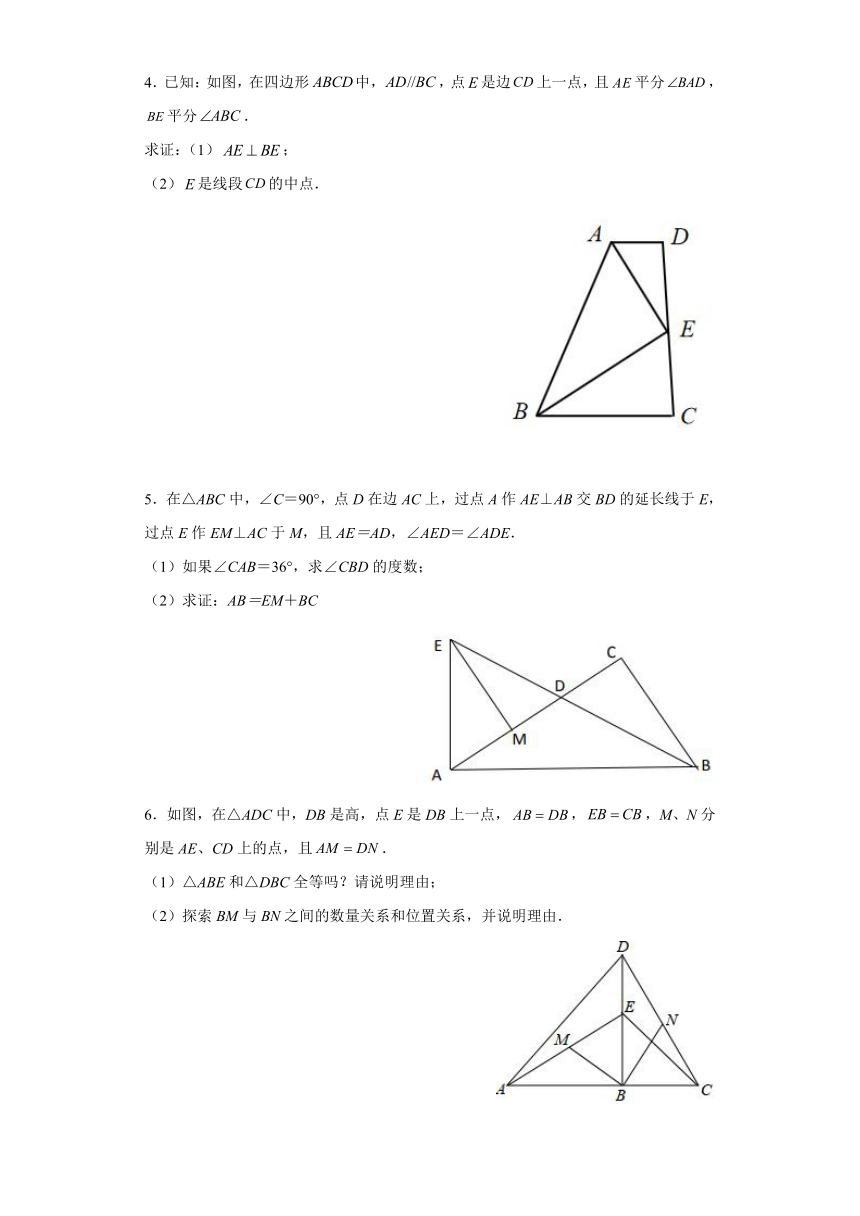
1.如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC.
(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BDC的度数.
2.已知:如图,AD、BF相交于点O,AB=DF.点E、C在BF上,且BE=FC,AC=DE.求证:OA=OD,OB=OF.
3.如图,在和中,,A、E、B、D在一条直线上,,,,垂足分别是E、B.求证:.
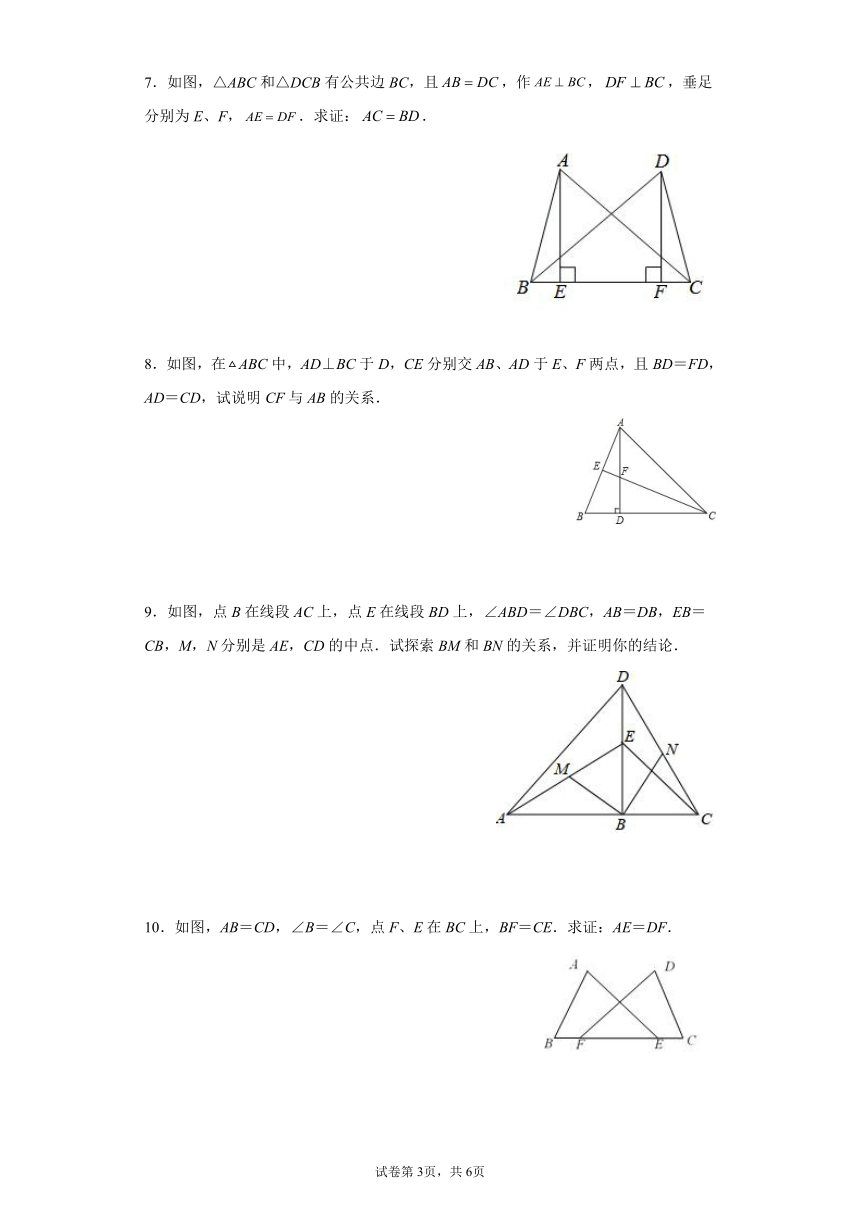
4.已知:如图,在四边形中,,点是边上一点,且平分,平分.
求证:(1);
(2)是线段的中点.
5.在△ABC中,∠C=90°,点D在边AC上,过点A作AE⊥AB交BD的延长线于E,过点E作EM⊥AC于M,且AE=AD,∠AED=∠ADE.
(1)如果∠CAB=36°,求∠CBD的度数;
(2)求证:AB=EM+BC
6.如图,在△ADC中,DB是高,点E是DB上一点,,,M、N分别是AE、CD上的点,且.
(1)△ABE和△DBC全等吗?请说明理由;
(2)探索BM与BN之间的数量关系和位置关系,并说明理由.
7.如图,△ABC和△DCB有公共边BC,且,作,,垂足分别为E、F,.求证:.
8.如图,在ABC中,AD⊥BC于D,CE分别交AB、AD于E、F两点,且BD=FD,AD=CD,试说明CF与AB的关系.
9.如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点.试探索BM和BN的关系,并证明你的结论.
10.如图,AB=CD,∠B=∠C,点F、E在BC上,BF=CE.求证:AE=DF.
11.如图,在和中,,延长分别交边、于点F、G.
(1)求证:.
(2)若,求的度数.
12.如图,线段AD上有两点E,B,且AE=DB,分别以AB,DE为直角边在线段AD同侧作Rt△ABC和Rt△DEF,∠A=∠D=90°,BC=EF.求证:∠AEG=∠DBG.
13.如图,在△ABC中,∠BAC=34°,∠ABC=110°,且DE⊥AB于E,DF⊥AC于F,DE=DF.求∠ADB的度数.
14.如图,,,,,垂足分别为,,,,求的长.
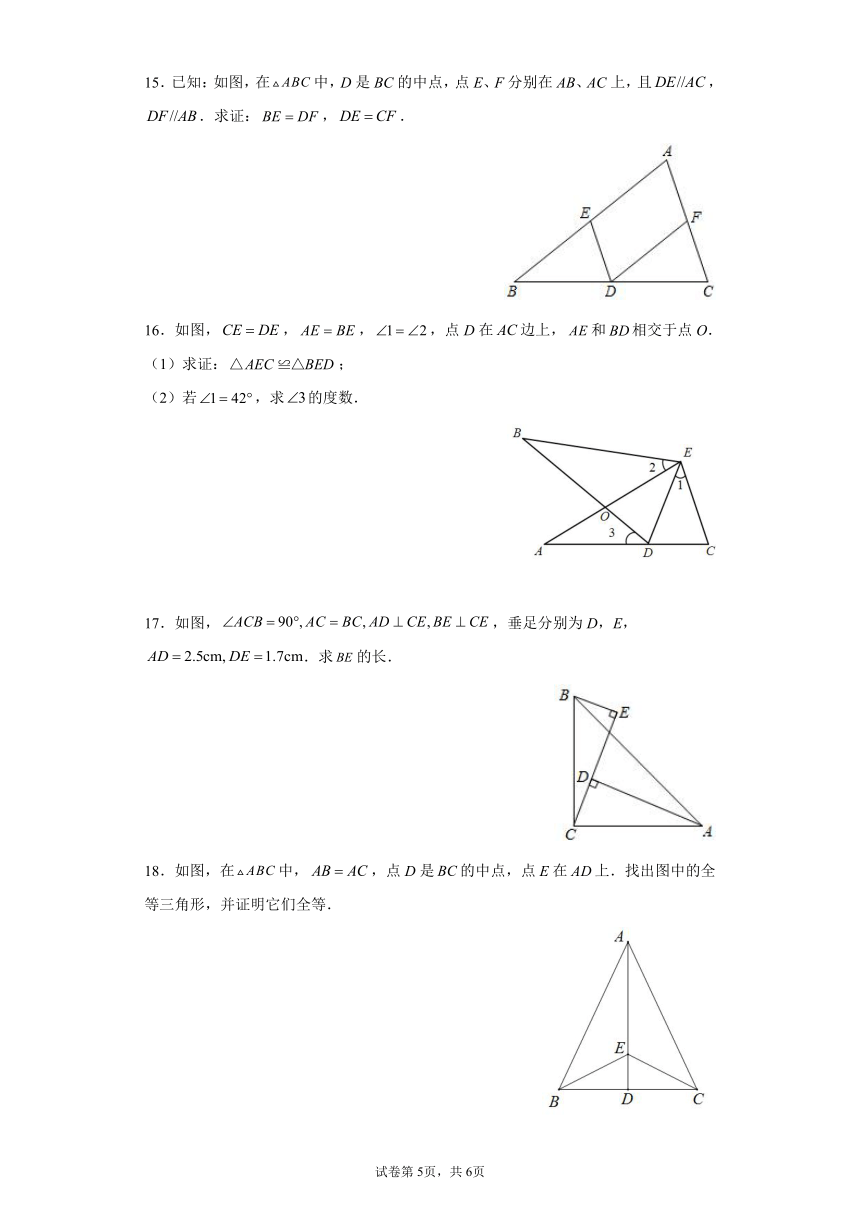
15.已知:如图,在中,D是BC的中点,点E、F分别在AB、AC上,且,.求证:,.
16.如图,,,,点D在边上,和相交于点O.
(1)求证:;
(2)若,求的度数.
17.如图,,垂足分别为D,E,.求的长.
18.如图,在中,,点D是的中点,点E在上.找出图中的全等三角形,并证明它们全等.
19.如图,已知:AB=AC,AD=AE,∠1=∠2,求证:∠B=∠C.
20.如图,AB∥FC,E是DF的中点.
(1)求证:△ADE≌△CFE;
(2)若AB=10,CF=6,求BD的长.
参考答案
1.
解:(1)证明:
∵∠ABC=90°,
∴∠DBC=90°,
在△ABE和△CBD中
,
∴△ABE≌△CBD(SAS);
(2)∵AB=CB,∠ABC=90°,
∴∠BCA=45°,
∴∠AEB=∠CAE+∠BCA=30°+45°=75°,
∵△ABE≌△CBD,
∴∠BDC=∠AEB=75°.
2.
证明:∵BE=CF,
∴BC=FE(等式的性质).
在△ABC和△DFE中,
,
∴△ABC≌△DFE(SSS),
∴∠ABF=∠DFB(全等三角形的对应角相等),
在△ABO和△DFO中,
,
∴△ABO≌△DFO(AAS),
∴OA=OD,OB=OF.
3.
证明:∵,,
∴,
在Rt△CBE和Rt△FBE中,
∴Rt△CBE≌Rt△FBE(HL),
∴,
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA),
∴AC=DF.
4.
解:(1),
,
又、分别平分、,
,
,
(2)如图,延长,交于,
,,
,
,
,且,
,
.
5.
解:(1)∵AE⊥AB,
∴∠EAB=90°,
∵∠CAB=36°,
∴∠EAC=∠EAB-∠CAB=54°,
∴,
∴∠CDB=∠ADE=63°,
∴∠CBD=180°-∠C-∠CDB=27°;
(2)如图,过点D作DF⊥AB于F,
∵EM⊥AD,DF⊥AB,
∴∠EMA=∠AFD=90°,
∴∠AEM+∠EAM=90°,
又∵∠EAM+∠FAD=90°,
∴∠AEM=∠DAF,
又∵AD=AE,
∴△AEM≌△DAF(AAS),
∴EM=AF,
∵∠AEB+∠ABE=90°,∠CDB+∠CBD=90°,∠AED=∠CDB=∠ADE,
∴∠FBD=∠CBD,
又∵∠C=∠DFB=90°,BD=BD,
∴△DFB≌△DCB(AAS),
∴BC=BF,
∵AB=AF+BF,
∴AB=EM+BC.
【点睛】
本题主要考查了全等三角形的性质与判定,三角形内角和定理,对顶角相等,垂直的定义,解题的关键在于能够熟练掌握全等三角形的性质与判定.
6.(1)△ABE和△DBC全等,理由见解析;(2)BM=BN,BM⊥BN;理由见解析.
【分析】
(1)先由DB是高可得∠ABE=∠DBC=90°,再结合已知则根据SAS可证明△ABE≌△DBC;
(2)利用全等三角形的性质证得∠BAM=∠BDN,则可由全等三角形的判定证明△ABM≌△DBN,得出BM=BN,∠ABM=∠DBN.得出∠MBN=90°,则结论得证.
【详解】
解:(1)△ABE≌△DBC;理由是:
∵DB是高,
∴∠ABE=∠DBC=90°.
在△ABE和△DBC中,
,
∴△ABE≌△DBC(SAS).
(2)BM=BN,MB⊥BN;理由是:
∵△ABE≌△DBC,
∴∠BAM=∠BDN.
在△ABM 和△DBN 中,
∴△ABM≌△DBN(SAS).
∴BM=BN,∠ABM=∠DBN.
∵∠ABM+∠DBM=∠ABD=90°.
∴∠DBN+∠DBM =90°.
即∠MBN=90°.
∴BM⊥BN.
【点睛】
本题主要考查了全等三角形的判定和性质、垂直的定义,熟练掌握全等三角形的判定和性质是解题的关键.
7.见解析
【分析】
需先根据HL判定Rt△ABE≌Rt△DCF,从而得出BE=CF,则推出EC=BF,再根据SAS判定△ABC≌△DCB,而求出AC=BD.
【详解】
证明:∵AE⊥BC,DF⊥BC,
∴∠AEB=∠DFC=90°,
∵AB=DC,AE=DF,
∴Rt△ABE≌Rt△DCF(HL).
∴∠ABE=∠DCF.
∵AB=DC,BC=CB,,
∴△ABC≌△DCB(SAS).
∴AC=BD.
【点睛】
此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键.
8.CF=AB,CF⊥AB,理由见解析
【分析】
先根据AD⊥BC可得,进而可利用“SAS”证明,由此可得,,进而即可证得.
【详解】
解:CF=AB,CF⊥AB,理由如下:
于,
,
在和中,
,
,
,,
∵,
,
,
,
.
9.
且.理由如下:
在与中,
,
,
,
M,N分别是AE,CD的中点,
,
在与中,
,
,
,,
,
,
且.
10.
证明:∵BF=CE,
∴BF+FE=CE+FE,
∴BE=CF,
在△ABE与△DCF中,
∵AB=DC,∠B=∠C,BE=CF,
∴△ABE≌△DCF(SAS).
∴AE=DF.
【点睛】
本题考查了全等三角形的判定和性质,掌握全等三角形的判定定理是本题的关键.
11.(1)见解析;(2)49°
【分析】
(1)运用SSS证明△ABC≌△ADE即可得证;
(2)利用三角形的内角和定理,等量代换计算即可.
【详解】
(1)∵AB=AD,AC=AE,BC=DE,
∴△ABC≌△ADE,
∴∠B=∠D.
(2)∵△ABC≌△ADE,
∴∠CAB=∠EAD,
∴∠DAB=∠CAE=49°.
∵∠B=∠D,∠DFG=∠BFA,
∴∠BGD=∠DAB=49°.
12.
证明:∵AE=DB
∴AE+EB=DB+EB,即AB=DE
∵∠A=∠D=90°
在Rt△ABC和Rt△DEF中
∴Rt△ABC≌Rt△DEF(HL)
∴∠ABC=∠DEF
∴∠AEG=∠DBG
13.
解:在中,,
,
,
和都是直角三角形,
在和中,,
,
,
.
14.
解:∵,,
∴,
∴.
∵,
∴.
在和中,
,
∴≌(AAS),
∴,,
∴.
15.
证明:∵D是BC的中点,
∴BD=DC,
∵,.
∴∠EBD=∠FDC,∠EDB=∠C,
在△EBD和△FDC中
∴△EBD≌△FDC(ASA),
∴,.
【点睛】
本题考查三角形全等判定与性质,平行线性质,中点定义,掌握三角形全等判定与性质,关键是熟知判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
16.(1)见解析;(2)
【分析】
(1)先证明,再根据SAS即可证明全等;
(2)利用三角形外角的性质可知,再根据全等可得,从而可得.
【详解】
解:(1)证明:∵,
∴,
即.
在和中,
,
∴
(2)∵,
∴.
∵,
∴.
17.
∵,,
∴,
∵,
∴.
∵,
∴.
∵,
∴.
∴,.
∴.
18
解:图中的全等三角形有:△ABD≌△ACD,△ABE≌△ACE,△BDE≌△CDE;
∵D是BC的中点,
∴BD=DC,AB=AC,AD=AD
∴△ABD≌△ACD(SSS);
∴∠BAE=∠CAE,在△ABE和△ACE中,
∵AE=AE,∠BAE=∠CAE,AB=AC,
∴△ABE≌△ACE;
∵△ABE≌△ACE,
∴BE=CE,
在△BDE和△CDE中,
∵BE=CE,BD=DC,DE=DE,
∴△BDE≌△CDE.
19.
解:∵∠1=∠2,
∴∠1+∠CAD=∠2+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中
,
∴△BAD≌△CAE(SAS),
∴∠B=∠C.
【点睛】
此题考查了全等三角形的判定与性质,解题的关键是熟练掌握全等三角形的判定方法.
20.(1)见解析;(2)4
【分析】
(1)根据平行得出,再用“角边角”证明即可;
(2)由(1)得,,再用线段和差即可求.
【详解】
解:(1)证明:∵,
∴,
∵是的中点,
∴,
在和中,
,
∴,
(2)∵,
∴,
∴.
试卷第5页,共6页
1.如图,在△ABC中,AB=CB,∠ABC=90°,D为AB延长线上一点,点E在BC边上,且BE=BD,连接AE、DE、DC.
(1)求证:△ABE≌△CBD;
(2)若∠CAE=30°,求∠BDC的度数.
2.已知:如图,AD、BF相交于点O,AB=DF.点E、C在BF上,且BE=FC,AC=DE.求证:OA=OD,OB=OF.
3.如图,在和中,,A、E、B、D在一条直线上,,,,垂足分别是E、B.求证:.
4.已知:如图,在四边形中,,点是边上一点,且平分,平分.
求证:(1);
(2)是线段的中点.
5.在△ABC中,∠C=90°,点D在边AC上,过点A作AE⊥AB交BD的延长线于E,过点E作EM⊥AC于M,且AE=AD,∠AED=∠ADE.
(1)如果∠CAB=36°,求∠CBD的度数;
(2)求证:AB=EM+BC
6.如图,在△ADC中,DB是高,点E是DB上一点,,,M、N分别是AE、CD上的点,且.
(1)△ABE和△DBC全等吗?请说明理由;
(2)探索BM与BN之间的数量关系和位置关系,并说明理由.
7.如图,△ABC和△DCB有公共边BC,且,作,,垂足分别为E、F,.求证:.
8.如图,在ABC中,AD⊥BC于D,CE分别交AB、AD于E、F两点,且BD=FD,AD=CD,试说明CF与AB的关系.
9.如图,点B在线段AC上,点E在线段BD上,∠ABD=∠DBC,AB=DB,EB=CB,M,N分别是AE,CD的中点.试探索BM和BN的关系,并证明你的结论.
10.如图,AB=CD,∠B=∠C,点F、E在BC上,BF=CE.求证:AE=DF.
11.如图,在和中,,延长分别交边、于点F、G.
(1)求证:.
(2)若,求的度数.
12.如图,线段AD上有两点E,B,且AE=DB,分别以AB,DE为直角边在线段AD同侧作Rt△ABC和Rt△DEF,∠A=∠D=90°,BC=EF.求证:∠AEG=∠DBG.
13.如图,在△ABC中,∠BAC=34°,∠ABC=110°,且DE⊥AB于E,DF⊥AC于F,DE=DF.求∠ADB的度数.
14.如图,,,,,垂足分别为,,,,求的长.
15.已知:如图,在中,D是BC的中点,点E、F分别在AB、AC上,且,.求证:,.
16.如图,,,,点D在边上,和相交于点O.
(1)求证:;
(2)若,求的度数.
17.如图,,垂足分别为D,E,.求的长.
18.如图,在中,,点D是的中点,点E在上.找出图中的全等三角形,并证明它们全等.
19.如图,已知:AB=AC,AD=AE,∠1=∠2,求证:∠B=∠C.
20.如图,AB∥FC,E是DF的中点.
(1)求证:△ADE≌△CFE;
(2)若AB=10,CF=6,求BD的长.
参考答案
1.
解:(1)证明:
∵∠ABC=90°,
∴∠DBC=90°,
在△ABE和△CBD中
,
∴△ABE≌△CBD(SAS);
(2)∵AB=CB,∠ABC=90°,
∴∠BCA=45°,
∴∠AEB=∠CAE+∠BCA=30°+45°=75°,
∵△ABE≌△CBD,
∴∠BDC=∠AEB=75°.
2.
证明:∵BE=CF,
∴BC=FE(等式的性质).
在△ABC和△DFE中,
,
∴△ABC≌△DFE(SSS),
∴∠ABF=∠DFB(全等三角形的对应角相等),
在△ABO和△DFO中,
,
∴△ABO≌△DFO(AAS),
∴OA=OD,OB=OF.
3.
证明:∵,,
∴,
在Rt△CBE和Rt△FBE中,
∴Rt△CBE≌Rt△FBE(HL),
∴,
在△ABC和△DEF中,
∴△ABC≌△DEF(ASA),
∴AC=DF.
4.
解:(1),
,
又、分别平分、,
,
,
(2)如图,延长,交于,
,,
,
,
,且,
,
.
5.
解:(1)∵AE⊥AB,
∴∠EAB=90°,
∵∠CAB=36°,
∴∠EAC=∠EAB-∠CAB=54°,
∴,
∴∠CDB=∠ADE=63°,
∴∠CBD=180°-∠C-∠CDB=27°;
(2)如图,过点D作DF⊥AB于F,
∵EM⊥AD,DF⊥AB,
∴∠EMA=∠AFD=90°,
∴∠AEM+∠EAM=90°,
又∵∠EAM+∠FAD=90°,
∴∠AEM=∠DAF,
又∵AD=AE,
∴△AEM≌△DAF(AAS),
∴EM=AF,
∵∠AEB+∠ABE=90°,∠CDB+∠CBD=90°,∠AED=∠CDB=∠ADE,
∴∠FBD=∠CBD,
又∵∠C=∠DFB=90°,BD=BD,
∴△DFB≌△DCB(AAS),
∴BC=BF,
∵AB=AF+BF,
∴AB=EM+BC.
【点睛】
本题主要考查了全等三角形的性质与判定,三角形内角和定理,对顶角相等,垂直的定义,解题的关键在于能够熟练掌握全等三角形的性质与判定.
6.(1)△ABE和△DBC全等,理由见解析;(2)BM=BN,BM⊥BN;理由见解析.
【分析】
(1)先由DB是高可得∠ABE=∠DBC=90°,再结合已知则根据SAS可证明△ABE≌△DBC;
(2)利用全等三角形的性质证得∠BAM=∠BDN,则可由全等三角形的判定证明△ABM≌△DBN,得出BM=BN,∠ABM=∠DBN.得出∠MBN=90°,则结论得证.
【详解】
解:(1)△ABE≌△DBC;理由是:
∵DB是高,
∴∠ABE=∠DBC=90°.
在△ABE和△DBC中,
,
∴△ABE≌△DBC(SAS).
(2)BM=BN,MB⊥BN;理由是:
∵△ABE≌△DBC,
∴∠BAM=∠BDN.
在△ABM 和△DBN 中,
∴△ABM≌△DBN(SAS).
∴BM=BN,∠ABM=∠DBN.
∵∠ABM+∠DBM=∠ABD=90°.
∴∠DBN+∠DBM =90°.
即∠MBN=90°.
∴BM⊥BN.
【点睛】
本题主要考查了全等三角形的判定和性质、垂直的定义,熟练掌握全等三角形的判定和性质是解题的关键.
7.见解析
【分析】
需先根据HL判定Rt△ABE≌Rt△DCF,从而得出BE=CF,则推出EC=BF,再根据SAS判定△ABC≌△DCB,而求出AC=BD.
【详解】
证明:∵AE⊥BC,DF⊥BC,
∴∠AEB=∠DFC=90°,
∵AB=DC,AE=DF,
∴Rt△ABE≌Rt△DCF(HL).
∴∠ABE=∠DCF.
∵AB=DC,BC=CB,,
∴△ABC≌△DCB(SAS).
∴AC=BD.
【点睛】
此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解题的关键.
8.CF=AB,CF⊥AB,理由见解析
【分析】
先根据AD⊥BC可得,进而可利用“SAS”证明,由此可得,,进而即可证得.
【详解】
解:CF=AB,CF⊥AB,理由如下:
于,
,
在和中,
,
,
,,
∵,
,
,
,
.
9.
且.理由如下:
在与中,
,
,
,
M,N分别是AE,CD的中点,
,
在与中,
,
,
,,
,
,
且.
10.
证明:∵BF=CE,
∴BF+FE=CE+FE,
∴BE=CF,
在△ABE与△DCF中,
∵AB=DC,∠B=∠C,BE=CF,
∴△ABE≌△DCF(SAS).
∴AE=DF.
【点睛】
本题考查了全等三角形的判定和性质,掌握全等三角形的判定定理是本题的关键.
11.(1)见解析;(2)49°
【分析】
(1)运用SSS证明△ABC≌△ADE即可得证;
(2)利用三角形的内角和定理,等量代换计算即可.
【详解】
(1)∵AB=AD,AC=AE,BC=DE,
∴△ABC≌△ADE,
∴∠B=∠D.
(2)∵△ABC≌△ADE,
∴∠CAB=∠EAD,
∴∠DAB=∠CAE=49°.
∵∠B=∠D,∠DFG=∠BFA,
∴∠BGD=∠DAB=49°.
12.
证明:∵AE=DB
∴AE+EB=DB+EB,即AB=DE
∵∠A=∠D=90°
在Rt△ABC和Rt△DEF中
∴Rt△ABC≌Rt△DEF(HL)
∴∠ABC=∠DEF
∴∠AEG=∠DBG
13.
解:在中,,
,
,
和都是直角三角形,
在和中,,
,
,
.
14.
解:∵,,
∴,
∴.
∵,
∴.
在和中,
,
∴≌(AAS),
∴,,
∴.
15.
证明:∵D是BC的中点,
∴BD=DC,
∵,.
∴∠EBD=∠FDC,∠EDB=∠C,
在△EBD和△FDC中
∴△EBD≌△FDC(ASA),
∴,.
【点睛】
本题考查三角形全等判定与性质,平行线性质,中点定义,掌握三角形全等判定与性质,关键是熟知判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.
16.(1)见解析;(2)
【分析】
(1)先证明,再根据SAS即可证明全等;
(2)利用三角形外角的性质可知,再根据全等可得,从而可得.
【详解】
解:(1)证明:∵,
∴,
即.
在和中,
,
∴
(2)∵,
∴.
∵,
∴.
17.
∵,,
∴,
∵,
∴.
∵,
∴.
∵,
∴.
∴,.
∴.
18
解:图中的全等三角形有:△ABD≌△ACD,△ABE≌△ACE,△BDE≌△CDE;
∵D是BC的中点,
∴BD=DC,AB=AC,AD=AD
∴△ABD≌△ACD(SSS);
∴∠BAE=∠CAE,在△ABE和△ACE中,
∵AE=AE,∠BAE=∠CAE,AB=AC,
∴△ABE≌△ACE;
∵△ABE≌△ACE,
∴BE=CE,
在△BDE和△CDE中,
∵BE=CE,BD=DC,DE=DE,
∴△BDE≌△CDE.
19.
解:∵∠1=∠2,
∴∠1+∠CAD=∠2+∠CAD,
∴∠BAD=∠CAE,
在△BAD和△CAE中
,
∴△BAD≌△CAE(SAS),
∴∠B=∠C.
【点睛】
此题考查了全等三角形的判定与性质,解题的关键是熟练掌握全等三角形的判定方法.
20.(1)见解析;(2)4
【分析】
(1)根据平行得出,再用“角边角”证明即可;
(2)由(1)得,,再用线段和差即可求.
【详解】
解:(1)证明:∵,
∴,
∵是的中点,
∴,
在和中,
,
∴,
(2)∵,
∴,
∴.
试卷第5页,共6页
