2020-2021学年人教版九年级数学上册第二十三章旋转 章末复习测试题(Word版含答案)
文档属性
| 名称 | 2020-2021学年人教版九年级数学上册第二十三章旋转 章末复习测试题(Word版含答案) |

|
|
| 格式 | doc | ||
| 文件大小 | 831.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 00:00:00 | ||
图片预览



文档简介
2020-2021学年人教版九年级数学上册 旋转 章末复习测试题
一、选择题
1. 下列现象属于旋转的是( )
A.摩托车在急刹车时向前滑动 B.空中飞舞的雪花
C.拧开自来水龙头的过程 D.飞机起飞后冲向空中的过程
2. 下列说法正确的是( )
A、平移不改变图形的形状和大小,而旋转则改变图形的形状和大小
B、平移和旋转的共同点是改变图形的位置
C、图形可以向某方向平移一定距离,也可以向某方向旋转一定距离
D、在平移和旋转图形中,对应角相等,对应线段相等且平行
3. 下列图案既是轴对称图形,又是中心对称图形的是( )
4. 将一图形绕着点O顺时针方向旋转70°后,再绕着点O逆时针方向旋转120°,这时如果要使图形回到原来的位置,需要将图形绕着点O什么方向旋转多少度?( )
A、顺时针方向,50° B、逆时针方向,50°
C、顺时针方向,190° D、逆时针方向,190°
5. 数学课上,老师让同学们观察如图所示的图形,问:它绕着圆心O旋转多少度后
和它自身重合?甲同学说:45°;乙同学说:60°;丙同学说:90°;丁同学说:135°.
以上四位同学的回答中,错误的是( )
A、甲 B、乙 C、丙 D、丁
6.如图,在正方形中,,点在上,且,点是上一动点,连接,将线段绕点逆时针旋转90°得到线段.要使点恰好落在 上, 则的长是( )
A.1 B.2 C.3 D.4
7. 如图,C是线段BD上一点,分别以BC、CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形对数有( ).
A.1对 B.2对 C.3对 D.4对
8. 如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在位置,A点落在位置,若,则的度数是( )
A、50° B、60° C、70° D、80°
9. 下列语句中,不正确的是( ).
图形平移是由移动的方向和距离所决定;
B.图形旋转是由旋转中心和旋转角度所决定;
C.中心对称图形是指一个图形绕其中的某一点旋转180°后能与其自身重合的图形;
D.旋转后能重合的图形也是中心对称图形.
10. 如图,点E是正方形ABCD内一点,把△BEC绕点C旋转至△DFC位置,则∠EFC的度数是( )
A.90° B.30° C.45° D.60°
11. 如图,边长为1的正方形绕点逆时针旋转到正方形,图
中阴影部分的面积为( )
B、 HYPERLINK "http:///" EMBED Equation.DSMT4 C、 D、
12. 如图,8×8方格纸上的两条对称轴EF、MN相交于中心点O,对△ABC分别作下列变换:
①先以点A为中心顺时针方向旋转90°,再向右平移4格、向上平移4格;
②先以点O为中心作中心对称图形,再以点A的对应点为中心逆时针方向旋转90°;
③先以直线MN为轴作轴对称图形,再向上平移4格,再以点A的对应点为中心顺时针方向旋转90°.其中,能将△ABC变换成△PQR的是( )
A、①② B、①③ C、②③ D、①②③
二、填空题
13. 如图,E、F分别是正方形ABCD的边BC、CD上一点,且BE+DF=EF,则∠EAF=_____.
14.如图,△ABC以点A为旋转中心,按逆时针方向旋转60°,得△AB'C',则△ABB'是____三角形。
15. 线段、两相交直线、角、等腰三角形、等边三角形、平行四边形、
矩形、菱形、正方形、圆等图形中是中心对称图形的有________________ __;既是轴对称图形,又是中心对称的图形有_ .
16.如图,△ABC以点A为旋转中心,按逆时针方向旋转60°,得到的△A是 三角形。
17. 如图,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,那么旋转中心是点______;旋转的度数是_____.
18. 如图,O是等边△ABC内一点,将△AOB绕B点逆时针旋转,使得B、O两点的对应点分别为C、D,则旋转角为_____________,图中除△ABC外,还有等边三形是______.
19. 如图,△ABC绕着点C顺时针旋转35°得到△C ,若⊥AC,则∠A的度数是 。
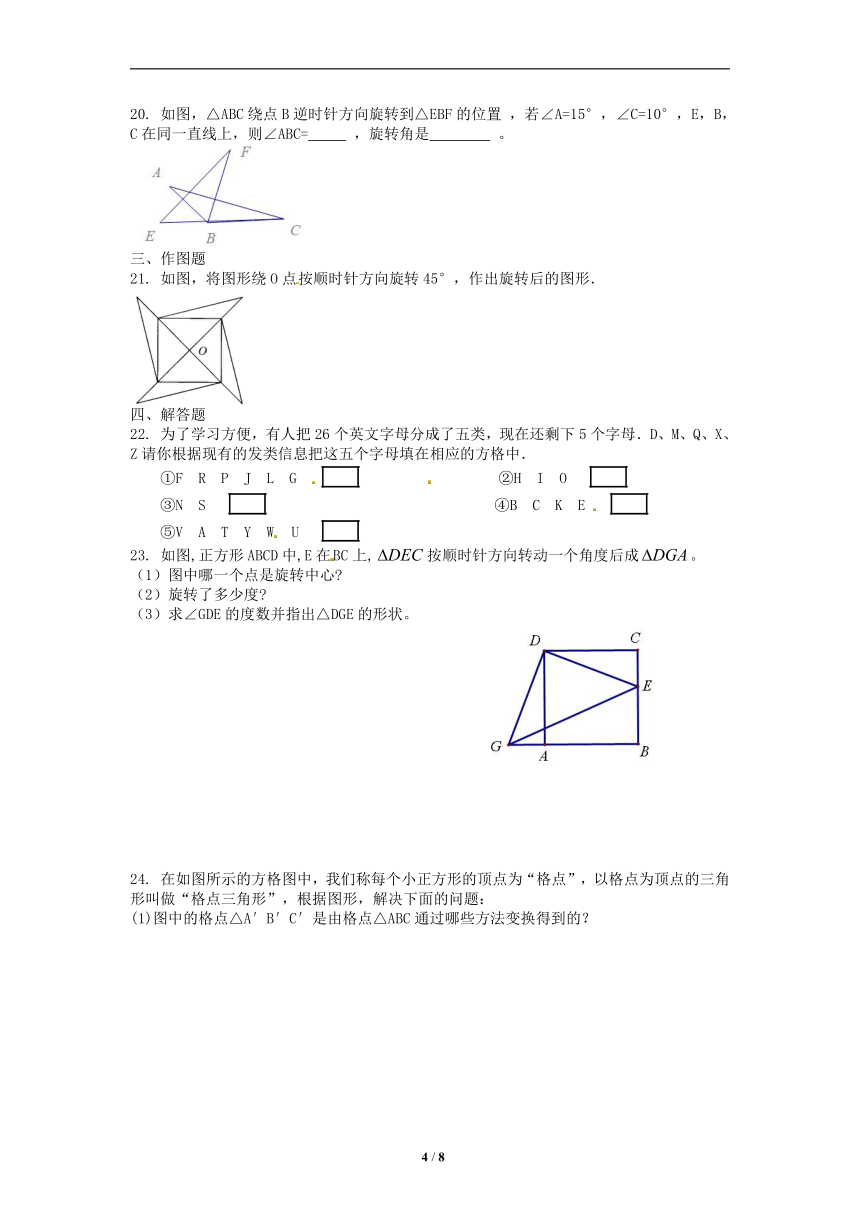
20. 如图,△ABC绕点B逆时针方向旋转到△EBF的位置 ,若∠A=15°,∠C=10°,E,B,C在同一直线上,则∠ABC= ,旋转角是 。
三、作图题
21. 如图,将图形绕O点按顺时针方向旋转45°,作出旋转后的图形.
四、解答题
22. 为了学习方便,有人把26个英文字母分成了五类,现在还剩下5个字母.D、M、Q、X、Z请你根据现有的发类信息把这五个字母填在相应的方格中.
①F R P J L G ②H I O
③N S ④B C K E
⑤V A T Y W U
23. 如图,正方形ABCD中,E在BC上,按顺时针方向转动一个角度后成。
(1)图中哪一个点是旋转中心
(2)旋转了多少度
(3)求∠GDE的度数并指出△DGE的形状。
24. 在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,解决下面的问题:
(1)图中的格点△A′B′C′是由格点△ABC通过哪些方法变换得到的?
(2)设每个小正方形的边长为1,如果建立平面直角坐标系后,点A的坐标为(-3,4),请写格点△DEF各顶点的坐标,并求出△DEF的面积.
25. 如图,的∠BAC=120 ,以BC为边向形外作等边,把绕着D点按顺时针方向旋转60 后到的位置。若,求∠BAD的度数和AD长.
26. 如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(-2,-2),B(-4,-1),C(-4,-4).
(1)作出△ABC关于原点O成中心对称的△A1B1C1.
(2)作出点A关于x轴的对称点A′.若把点A′向右平移a个单位长度后落在△A1B1C1的内部(不包括顶点和边界),求a的取值范围.
27. 阅读下面材料:
如图1,把△ABC沿直线BC平行移动线段BC的长度,可以变到△ECD的位置.
如图2,以BC为轴把△ABC翻折180°,可以变到△DBC的位置.
(1) (2) (3) (4)
如图3,以A点为中心,把△ABC旋转90°,可以变到△AED的位置,像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的,这种只改变位置,不改变形状和大小的图形变换,叫做三角形的全等变换.
回答下列问题
如图4,在正方形ABCD中,E是AD的中点,F是BA延长线上一点,AF=AB.
(1)在如图4所示,可以通过平行移动、翻折、旋转中的哪一种方法,使△ABE移到△ADF的位置?
(2)指出如图4所示中的线段BE与DF之间的关系.
28. 把两个全等的等腰直角三角板ABC和EFG(其直角边长均为4)叠放在一起,如图(1),且三角板EFG的直角顶点G与三角板ABC的斜边的中点O重合,现将三角板EFG绕点O顺时针方向旋转(旋转角α满足的条件:0°<α<90°),四边形CHGK是旋转过程中两个三角板的重叠部分,如图(2).
在上述旋转过程中,BH与CK有怎样的数量关系?四边形CHGK的面积有何变化?证明你发现的结论。
答案
一、选择题(本大题共12道小题)
1. 【答案】C
2. 【答案】B;
3. 【答案】B
4. 【答案】A;
5. 【答案】B
6. 【答案】C
7. 【答案】C
8. 【答案】C
9. 【答案】C
10. 【答案】C
11. 【答案】C
12. 【答案】D
二、填空题(本大题共8道小题)
13. 【答案】45°
14. 【答案】等边;
15. 【答案】线段、两相交直线、平行四边形;线段、两相交直线.
16. 【答案】等边
17. 【答案】A 45°
18. 【答案】60°;△AOD
19. 【答案】55°
20. 【答案】155° 25°
三、作图题
21. 【答案】略。
四、解答题
22. 【答案】解:①Q ②X ③Z ④D ⑤M
点拨:第①组字母即非中心对称图形,又不是轴对称图形,在剩下的5个字母中只有Q符合这个条件;第②组字母既是中心对称图形,又是轴对称图形,符合条件的字母是X;第③组字母不是轴对称图形,而是中心对称图形,符合条件的字母是Z.第④组字母仅是轴对称图形,且对称轴为水平的直线,符合这个条件的字母是D.第⑤组字母仅是轴对称图形,而对称轴为竖直的直线,符合条件的字母只有M.
23. 【答案】(1) 点D (2) 90 (3)∠GDE=90 △DGE是等腰直角三角形
24. 【答案】(1)方法不唯一,如:先把△ABC向右平移5小格,使点C移到点C′,再以点C′为旋转中心,顺时针方向旋转90°得到△A′B′C′.
(2)D(0,-2),E(-4,-4),F(2,-3),显然点G在DE上,且是DE的中点,则S△DEF=S△DGF+S△GFE==4.
25. 【答案】 600,5
26. 【答案】【思维教练】要作△ABC关于点O的中心对称图形,可先分别求出点A,B,C关于点O 中心对称点,再顺次连接即可;(2)先作出点A′,再根据点A′在ΔA1B1C1,从而得出平移距离a满足A′A1解:(1)如解图,△A1B1C1就是所求作的图形:(2分)
(2)A′如图所示;(4分)
a的取值范围是4<a<6.(6分)
27. 【答案】(1)通过旋转,即以点A为旋转中心,将△ABE逆时针旋转90°.
(2)BE=DF,BE⊥DF
28. 【答案】BH=CK ;因为△GBH≌△GCK.此四边形的面积保持不变,总等于原直角三角形面积的一半.
1 / 3
一、选择题
1. 下列现象属于旋转的是( )
A.摩托车在急刹车时向前滑动 B.空中飞舞的雪花
C.拧开自来水龙头的过程 D.飞机起飞后冲向空中的过程
2. 下列说法正确的是( )
A、平移不改变图形的形状和大小,而旋转则改变图形的形状和大小
B、平移和旋转的共同点是改变图形的位置
C、图形可以向某方向平移一定距离,也可以向某方向旋转一定距离
D、在平移和旋转图形中,对应角相等,对应线段相等且平行
3. 下列图案既是轴对称图形,又是中心对称图形的是( )
4. 将一图形绕着点O顺时针方向旋转70°后,再绕着点O逆时针方向旋转120°,这时如果要使图形回到原来的位置,需要将图形绕着点O什么方向旋转多少度?( )
A、顺时针方向,50° B、逆时针方向,50°
C、顺时针方向,190° D、逆时针方向,190°
5. 数学课上,老师让同学们观察如图所示的图形,问:它绕着圆心O旋转多少度后
和它自身重合?甲同学说:45°;乙同学说:60°;丙同学说:90°;丁同学说:135°.
以上四位同学的回答中,错误的是( )
A、甲 B、乙 C、丙 D、丁
6.如图,在正方形中,,点在上,且,点是上一动点,连接,将线段绕点逆时针旋转90°得到线段.要使点恰好落在 上, 则的长是( )
A.1 B.2 C.3 D.4
7. 如图,C是线段BD上一点,分别以BC、CD为边在BD同侧作等边△ABC和等边△CDE,AD交CE于F,BE交AC于G,则图中可通过旋转而相互得到的三角形对数有( ).
A.1对 B.2对 C.3对 D.4对
8. 如图,将△ABC绕着点C按顺时针方向旋转20°,B点落在位置,A点落在位置,若,则的度数是( )
A、50° B、60° C、70° D、80°
9. 下列语句中,不正确的是( ).
图形平移是由移动的方向和距离所决定;
B.图形旋转是由旋转中心和旋转角度所决定;
C.中心对称图形是指一个图形绕其中的某一点旋转180°后能与其自身重合的图形;
D.旋转后能重合的图形也是中心对称图形.
10. 如图,点E是正方形ABCD内一点,把△BEC绕点C旋转至△DFC位置,则∠EFC的度数是( )
A.90° B.30° C.45° D.60°
11. 如图,边长为1的正方形绕点逆时针旋转到正方形,图
中阴影部分的面积为( )
B、 HYPERLINK "http:///" EMBED Equation.DSMT4 C、 D、
12. 如图,8×8方格纸上的两条对称轴EF、MN相交于中心点O,对△ABC分别作下列变换:
①先以点A为中心顺时针方向旋转90°,再向右平移4格、向上平移4格;
②先以点O为中心作中心对称图形,再以点A的对应点为中心逆时针方向旋转90°;
③先以直线MN为轴作轴对称图形,再向上平移4格,再以点A的对应点为中心顺时针方向旋转90°.其中,能将△ABC变换成△PQR的是( )
A、①② B、①③ C、②③ D、①②③
二、填空题
13. 如图,E、F分别是正方形ABCD的边BC、CD上一点,且BE+DF=EF,则∠EAF=_____.
14.如图,△ABC以点A为旋转中心,按逆时针方向旋转60°,得△AB'C',则△ABB'是____三角形。
15. 线段、两相交直线、角、等腰三角形、等边三角形、平行四边形、
矩形、菱形、正方形、圆等图形中是中心对称图形的有________________ __;既是轴对称图形,又是中心对称的图形有_ .
16.如图,△ABC以点A为旋转中心,按逆时针方向旋转60°,得到的△A是 三角形。
17. 如图,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果△ABC经旋转后能与△ADE重合,那么旋转中心是点______;旋转的度数是_____.
18. 如图,O是等边△ABC内一点,将△AOB绕B点逆时针旋转,使得B、O两点的对应点分别为C、D,则旋转角为_____________,图中除△ABC外,还有等边三形是______.
19. 如图,△ABC绕着点C顺时针旋转35°得到△C ,若⊥AC,则∠A的度数是 。
20. 如图,△ABC绕点B逆时针方向旋转到△EBF的位置 ,若∠A=15°,∠C=10°,E,B,C在同一直线上,则∠ABC= ,旋转角是 。
三、作图题
21. 如图,将图形绕O点按顺时针方向旋转45°,作出旋转后的图形.
四、解答题
22. 为了学习方便,有人把26个英文字母分成了五类,现在还剩下5个字母.D、M、Q、X、Z请你根据现有的发类信息把这五个字母填在相应的方格中.
①F R P J L G ②H I O
③N S ④B C K E
⑤V A T Y W U
23. 如图,正方形ABCD中,E在BC上,按顺时针方向转动一个角度后成。
(1)图中哪一个点是旋转中心
(2)旋转了多少度
(3)求∠GDE的度数并指出△DGE的形状。
24. 在如图所示的方格图中,我们称每个小正方形的顶点为“格点”,以格点为顶点的三角形叫做“格点三角形”,根据图形,解决下面的问题:
(1)图中的格点△A′B′C′是由格点△ABC通过哪些方法变换得到的?
(2)设每个小正方形的边长为1,如果建立平面直角坐标系后,点A的坐标为(-3,4),请写格点△DEF各顶点的坐标,并求出△DEF的面积.
25. 如图,的∠BAC=120 ,以BC为边向形外作等边,把绕着D点按顺时针方向旋转60 后到的位置。若,求∠BAD的度数和AD长.
26. 如图,在平面直角坐标系中,△ABC各顶点的坐标分别为A(-2,-2),B(-4,-1),C(-4,-4).
(1)作出△ABC关于原点O成中心对称的△A1B1C1.
(2)作出点A关于x轴的对称点A′.若把点A′向右平移a个单位长度后落在△A1B1C1的内部(不包括顶点和边界),求a的取值范围.
27. 阅读下面材料:
如图1,把△ABC沿直线BC平行移动线段BC的长度,可以变到△ECD的位置.
如图2,以BC为轴把△ABC翻折180°,可以变到△DBC的位置.
(1) (2) (3) (4)
如图3,以A点为中心,把△ABC旋转90°,可以变到△AED的位置,像这样,其中一个三角形是由另一个三角形按平行移动、翻折、旋转等方法变成的,这种只改变位置,不改变形状和大小的图形变换,叫做三角形的全等变换.
回答下列问题
如图4,在正方形ABCD中,E是AD的中点,F是BA延长线上一点,AF=AB.
(1)在如图4所示,可以通过平行移动、翻折、旋转中的哪一种方法,使△ABE移到△ADF的位置?
(2)指出如图4所示中的线段BE与DF之间的关系.
28. 把两个全等的等腰直角三角板ABC和EFG(其直角边长均为4)叠放在一起,如图(1),且三角板EFG的直角顶点G与三角板ABC的斜边的中点O重合,现将三角板EFG绕点O顺时针方向旋转(旋转角α满足的条件:0°<α<90°),四边形CHGK是旋转过程中两个三角板的重叠部分,如图(2).
在上述旋转过程中,BH与CK有怎样的数量关系?四边形CHGK的面积有何变化?证明你发现的结论。
答案
一、选择题(本大题共12道小题)
1. 【答案】C
2. 【答案】B;
3. 【答案】B
4. 【答案】A;
5. 【答案】B
6. 【答案】C
7. 【答案】C
8. 【答案】C
9. 【答案】C
10. 【答案】C
11. 【答案】C
12. 【答案】D
二、填空题(本大题共8道小题)
13. 【答案】45°
14. 【答案】等边;
15. 【答案】线段、两相交直线、平行四边形;线段、两相交直线.
16. 【答案】等边
17. 【答案】A 45°
18. 【答案】60°;△AOD
19. 【答案】55°
20. 【答案】155° 25°
三、作图题
21. 【答案】略。
四、解答题
22. 【答案】解:①Q ②X ③Z ④D ⑤M
点拨:第①组字母即非中心对称图形,又不是轴对称图形,在剩下的5个字母中只有Q符合这个条件;第②组字母既是中心对称图形,又是轴对称图形,符合条件的字母是X;第③组字母不是轴对称图形,而是中心对称图形,符合条件的字母是Z.第④组字母仅是轴对称图形,且对称轴为水平的直线,符合这个条件的字母是D.第⑤组字母仅是轴对称图形,而对称轴为竖直的直线,符合条件的字母只有M.
23. 【答案】(1) 点D (2) 90 (3)∠GDE=90 △DGE是等腰直角三角形
24. 【答案】(1)方法不唯一,如:先把△ABC向右平移5小格,使点C移到点C′,再以点C′为旋转中心,顺时针方向旋转90°得到△A′B′C′.
(2)D(0,-2),E(-4,-4),F(2,-3),显然点G在DE上,且是DE的中点,则S△DEF=S△DGF+S△GFE==4.
25. 【答案】 600,5
26. 【答案】【思维教练】要作△ABC关于点O的中心对称图形,可先分别求出点A,B,C关于点O 中心对称点,再顺次连接即可;(2)先作出点A′,再根据点A′在ΔA1B1C1,从而得出平移距离a满足A′A1
(2)A′如图所示;(4分)
a的取值范围是4<a<6.(6分)
27. 【答案】(1)通过旋转,即以点A为旋转中心,将△ABE逆时针旋转90°.
(2)BE=DF,BE⊥DF
28. 【答案】BH=CK ;因为△GBH≌△GCK.此四边形的面积保持不变,总等于原直角三角形面积的一半.
1 / 3
同课章节目录
