4.4.2对数函数的图像和性质 课件(共28张PPT)
文档属性
| 名称 | 4.4.2对数函数的图像和性质 课件(共28张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 2.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 16:50:42 | ||
图片预览




文档简介
(共28张PPT)
4.4.2对数函数的图像和性质
人教A(2019)版
必修一
新知导入
复习巩固
对数函数的定义
1、判断下列函数是不是对数函数:
×
√
√
×
√
X
×
×
2、已知函数f(x)为对数函数,且图象过点(4, 2),求f(1),f(8)
新知导入
下面我们探究对数函数的图像和性质
新知讲解
研究函数的一般步骤:
(一)掌握定义(二)画出图像(三)探求性质
在图像的基础上探求性质应从以下几个方面:
①定义域 ②值域 ③单调性 ④奇偶性 ⑤特殊点
新知讲解
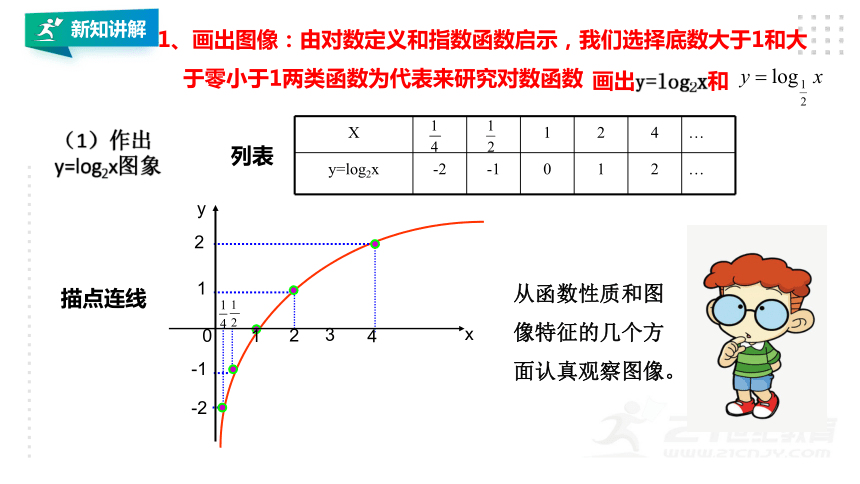
1、画出图像:由对数定义和指数函数启示,我们选择底数大于1和大
于零小于1两类函数为代表来研究对数函数
(1)作出
y=log2x图象
X 1 2 4 …
y=log2x -2 -1 0 1 2 …
列表
描点连线
2
1
-1
-2
1
2
4
0
y
x
3
画出y=log2x和
从函数性质和图
像特征的几个方
面认真观察图像。
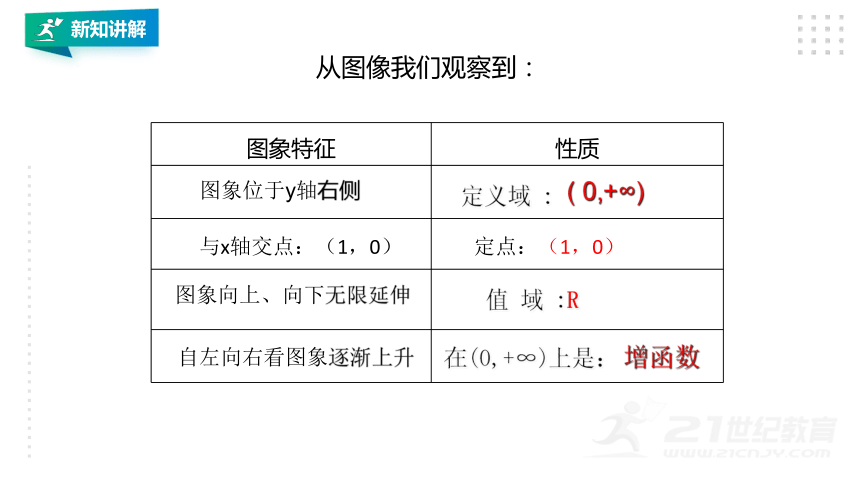
图象特征 性质
图象位于y轴右侧
定义域 :
( 0,+∞)
图象向上、向下无限延伸
值 域 :R
自左向右看图象逐渐上升
在(0,+∞)上是:
增函数
定点:(1,0)
从图像我们观察到:
与x轴交点:(1,0)
新知讲解
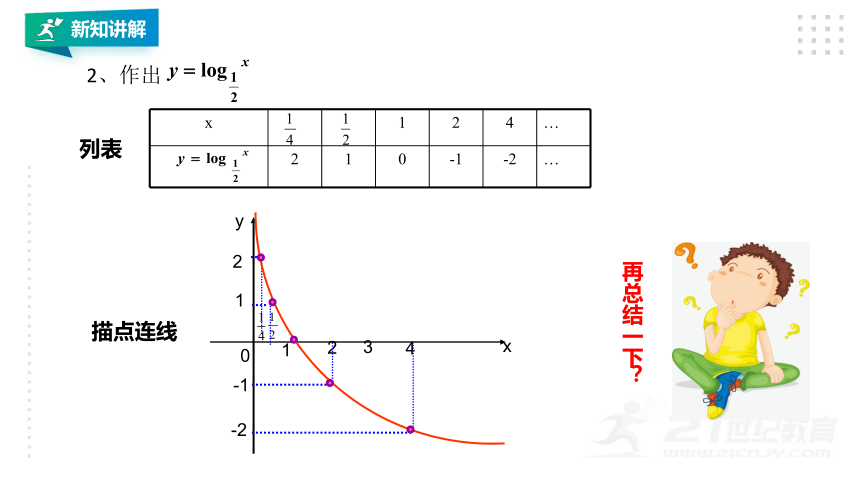
2、作出
x 1 2 4 …
2 1 0 -1 -2 …
2
1
-1
-2
1
2
4
0
y
x
3
列表
描点连线
新知讲解
再总结一下?
新知讲解
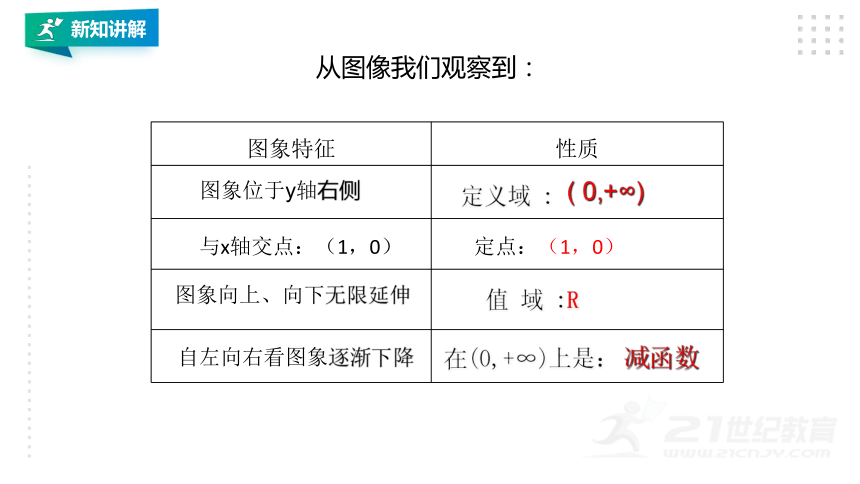
图象特征 性质
图象位于y轴右侧
定义域 :
( 0,+∞)
图象向上、向下无限延伸
值 域 :R
自左向右看图象逐渐下降
在(0,+∞)上是:
减函数
定点:(1,0)
从图像我们观察到:
与x轴交点:(1,0)
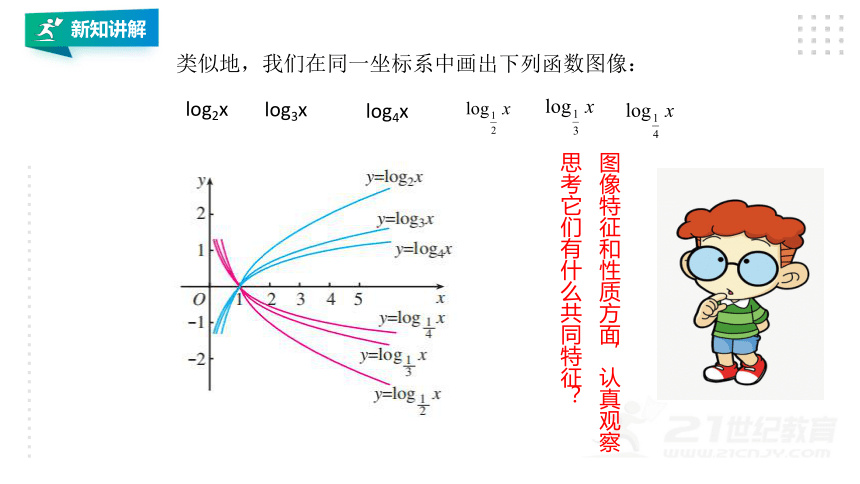
类似地,我们在同一坐标系中画出下列函数图像:
log2x
log3x
log4x
图像特征和性质方面,认真观察
思考它们有什么共同特征?
新知讲解
新知讲解
综合上述分析,我们总结出对数函数的图象和性质
a>1
图 象
0y
X
O
x =1
(1,0)
y
X
O
x =1
(1,0)
当x>1时,y>0; 当0当x>1时,y<0; 当00.
特
征
性 质 定义域 值域 特殊点 单调性
奇偶性
最值 (0,+ )
(0,+ )
R
R
过点(1,0)
过点(1,0)
在(0,+ )上是增函数
在(0,+ )上是减函数
非奇非偶函数
非奇非偶函数
无最值
无最值
合作探究
例1、 比较下列各组数中两个值的大小:
⑴ log 23.4 , log 28.5 ⑵ log 0.31.8 , log 0.32.7 ⑶ log a5.1 , log a5.9 ( a>0 , a≠1 )
解:⑴∵对数函数y = log 2x
在(0,+∞)上是增函数
且 3.4<8.5
∴ log 23.4<log 28.5
⑵∵对数函数 y = log0.3x,
在(0,+∞)上是减函数,
∴log 0.31.8>log 0.32.7
且1.8<2.7
(3)当a>1时,函数y=log ax在(0,+∞)上是增函数,于是
当0<a<1时,函数y=log ax在(0,+∞)上是减函数,于是
log a5.1<log a5.9
log a5.1>log a5.9
例2、溶液酸碱度的测量. 溶液酸碱度是通过PH计量的.PH的计算公式为PH=-lg[H+],其中[H+]表示溶液中氢离子的浓度,单位是摩尔/升.
(1)根据对数函数性质及上述pH的计算公式,说明溶液酸碱度与溶液中氢离子的浓度之间的变化关系;
(2)已知纯净水中氢离子的浓度为 [H+]=10-7摩尔/升,计算纯净水的PH
解:(1)根据对数的运算性质,有
PH=-lg[H+]=lg[H+]-1=
在(0,+∞)上,随着[H+]的增大, 减小,相应地, 也减小,即PH减小.所以,随着[H+]的增大,PH减小,即溶液中氢离子的浓度越大,溶液的酸性就越强.
(2)当[H+]=10-7时,PH=-lg10-7=7.所以,纯净水的pH是7.
合作探究
合作探究
例3. 求不等式log2(4x+8)>log22x 的解集.
解:由对数函数的性质及定义域要求,得
4x+8>0
2x>0
4x+8>2x
x > -2
x> -4
x>0
∴ x>0
解对数不等式时 , 注意真数大于零的条件限制.
例4、求函数 恒过的定点.
解:令x-2=1, 得x=3, 则y=loga1+1=1
所以函数恒过定点(3,1)
合作探究
例5、比较 log53 、log43大小:
解:
在同一坐标系中带出log5x和log4x对数函数图象,如图:
x
o
y
1
y1=log4x
y2=log5x
3
当底数不相同,真数相同时,利用图象判断大小.
方法
例6、求函数 的单调区间.
合作探究
分析:根据复合函数“同增异减”的单调性判断方法去判断。
解:令u=x2-3x+2,且u>0, 化为
而函数u在(-∝,1)单调递减,在(2,+∝)单调递增。
在(0,+∝)上单调递减
由复合函数单调性的判断:
在(-∝,1)上单调递增;在(2,+∝)单调递减.
合作探究
例7、求函数y=log2(x2+2x+17)的值域。
解:令u=x2+2x+17=(x+1)2+16≥16
又因为y=log2x是增函数,
所以,y=log2(x2+2x+17)=log2u
故y=log2(x2+2x+17)=log2u≥log216=4
所以,y=log2(x2+2x+17)的值域[4,+∝)
合作探究
我们观察函数y=2x与y=log2x 的图象关系,观察它们的图像:
在研究指数与对数时我们发现它们是密不可分的
那它们存在怎样的内存联系呢?
2
1
-1
-2
1
2
4
0
y
x
3
y=log2x
y=x
A ●
● A’
B ●
●
B’
y=2x
我们发现它们的图象关于直线y=x对称。
合作探究
再来观察
2
1
-1
-2
1
2
4
0
y
x
3
y=x
● B
●
B’
我们发现它们的图象也是关于直线y=x对称。
我们归纳得到结论:y=ax与y=logax图象关于直线y=x对称。
合作探究
反函数的定义
前面根据指数与对数间的关系,由 .由函数定义可知 是一个函数.这样,由指数函数 可得到对数函数 .这个对数函数的定义域 (0、1]值域
[0,+∞)分别是指数函数 的值域和定义域.
这时就说函数 是函数 的反函数.
像y=ax和x=logay 这样的两个函数叫作互为反函数.
通常情况下,用x 表示自变量, y表示函数,所以,指数函数y=ax 是对数函数 y=logax的反函数;同时,对数函数y=logax 是指数函数y=ax的反函数。
合作探究
例3:
写出下列函数的反函数:
(1) y=lgx (2) y=log0.5x
(3) y=5x (4) y=(0.8)x
解:
(1) y=10x
(2) y=(0.5)x
(3)
y=log5x
y=log0.8x
(4)
课堂练习
1、比较下列各组中,两个值的大小:
(1) Log23与 Log23.5 (2) Log 0.7 1.6与 Log 0.7 1.8
解1:考察函数y=log2 x ,
∵a=2 > 1, ∴函数在区间(0,+∞)上是增函数;
∵3<3.5 ∴ log23< log23.5
解2:考察函数y=log0.7 x ,
∵a=0.7< 1, ∴函数在区间(0,+∞)上是减函数;
∵1.6<1.8 ∴ log 0.7 1.6> log 0.7 1.8
课堂练习
2、求函数 的定义域.
解:
即
课堂练习
3、比较下列各组数字的大小
(1) log23.4>log28.5
(2) log0.31.8(3) 当0loga5.1>loga5.9
当a>1时,
loga5.1(4) log67>log76
(5) 1.10.9>log0.70.8>log1.10.9
课堂总结
对数函数图像
y
X
O
x =1
(1,0)
y
X
O
x =1
(1,0)
对数函数性质
性 质 定义域 值域 特殊点 单调性
奇偶性
最值 (0,+ )
(0,+ )
R
R
过点(1,0)
过点(1,0)
在(0,+ )上是增函数
在(0,+ )上是减函数
非奇非偶函数
非奇非偶函数
无最值
无最值
a>1
0板书设计
对数函数图像
对数函数的性质
定义域
(0,+ )
值域
R
单调性
a>1
0在(0,+ )上是增函数
在(0,+ )上是减函数
性质的应用
作业布置
3、课本P135练习1、2、3
1、求函数y=loga(2x+1)-2 恒过的定点.
2、求函数 的单调区间及值域。
https://www.21cnjy.com/help/help_extract.php
4.4.2对数函数的图像和性质
人教A(2019)版
必修一
新知导入
复习巩固
对数函数的定义
1、判断下列函数是不是对数函数:
×
√
√
×
√
X
×
×
2、已知函数f(x)为对数函数,且图象过点(4, 2),求f(1),f(8)
新知导入
下面我们探究对数函数的图像和性质
新知讲解
研究函数的一般步骤:
(一)掌握定义(二)画出图像(三)探求性质
在图像的基础上探求性质应从以下几个方面:
①定义域 ②值域 ③单调性 ④奇偶性 ⑤特殊点
新知讲解
1、画出图像:由对数定义和指数函数启示,我们选择底数大于1和大
于零小于1两类函数为代表来研究对数函数
(1)作出
y=log2x图象
X 1 2 4 …
y=log2x -2 -1 0 1 2 …
列表
描点连线
2
1
-1
-2
1
2
4
0
y
x
3
画出y=log2x和
从函数性质和图
像特征的几个方
面认真观察图像。
图象特征 性质
图象位于y轴右侧
定义域 :
( 0,+∞)
图象向上、向下无限延伸
值 域 :R
自左向右看图象逐渐上升
在(0,+∞)上是:
增函数
定点:(1,0)
从图像我们观察到:
与x轴交点:(1,0)
新知讲解
2、作出
x 1 2 4 …
2 1 0 -1 -2 …
2
1
-1
-2
1
2
4
0
y
x
3
列表
描点连线
新知讲解
再总结一下?
新知讲解
图象特征 性质
图象位于y轴右侧
定义域 :
( 0,+∞)
图象向上、向下无限延伸
值 域 :R
自左向右看图象逐渐下降
在(0,+∞)上是:
减函数
定点:(1,0)
从图像我们观察到:
与x轴交点:(1,0)
类似地,我们在同一坐标系中画出下列函数图像:
log2x
log3x
log4x
图像特征和性质方面,认真观察
思考它们有什么共同特征?
新知讲解
新知讲解
综合上述分析,我们总结出对数函数的图象和性质
a>1
图 象
0
X
O
x =1
(1,0)
y
X
O
x =1
(1,0)
当x>1时,y>0; 当0
特
征
性 质 定义域 值域 特殊点 单调性
奇偶性
最值 (0,+ )
(0,+ )
R
R
过点(1,0)
过点(1,0)
在(0,+ )上是增函数
在(0,+ )上是减函数
非奇非偶函数
非奇非偶函数
无最值
无最值
合作探究
例1、 比较下列各组数中两个值的大小:
⑴ log 23.4 , log 28.5 ⑵ log 0.31.8 , log 0.32.7 ⑶ log a5.1 , log a5.9 ( a>0 , a≠1 )
解:⑴∵对数函数y = log 2x
在(0,+∞)上是增函数
且 3.4<8.5
∴ log 23.4<log 28.5
⑵∵对数函数 y = log0.3x,
在(0,+∞)上是减函数,
∴log 0.31.8>log 0.32.7
且1.8<2.7
(3)当a>1时,函数y=log ax在(0,+∞)上是增函数,于是
当0<a<1时,函数y=log ax在(0,+∞)上是减函数,于是
log a5.1<log a5.9
log a5.1>log a5.9
例2、溶液酸碱度的测量. 溶液酸碱度是通过PH计量的.PH的计算公式为PH=-lg[H+],其中[H+]表示溶液中氢离子的浓度,单位是摩尔/升.
(1)根据对数函数性质及上述pH的计算公式,说明溶液酸碱度与溶液中氢离子的浓度之间的变化关系;
(2)已知纯净水中氢离子的浓度为 [H+]=10-7摩尔/升,计算纯净水的PH
解:(1)根据对数的运算性质,有
PH=-lg[H+]=lg[H+]-1=
在(0,+∞)上,随着[H+]的增大, 减小,相应地, 也减小,即PH减小.所以,随着[H+]的增大,PH减小,即溶液中氢离子的浓度越大,溶液的酸性就越强.
(2)当[H+]=10-7时,PH=-lg10-7=7.所以,纯净水的pH是7.
合作探究
合作探究
例3. 求不等式log2(4x+8)>log22x 的解集.
解:由对数函数的性质及定义域要求,得
4x+8>0
2x>0
4x+8>2x
x > -2
x> -4
x>0
∴ x>0
解对数不等式时 , 注意真数大于零的条件限制.
例4、求函数 恒过的定点.
解:令x-2=1, 得x=3, 则y=loga1+1=1
所以函数恒过定点(3,1)
合作探究
例5、比较 log53 、log43大小:
解:
在同一坐标系中带出log5x和log4x对数函数图象,如图:
x
o
y
1
y1=log4x
y2=log5x
3
当底数不相同,真数相同时,利用图象判断大小.
方法
例6、求函数 的单调区间.
合作探究
分析:根据复合函数“同增异减”的单调性判断方法去判断。
解:令u=x2-3x+2,且u>0, 化为
而函数u在(-∝,1)单调递减,在(2,+∝)单调递增。
在(0,+∝)上单调递减
由复合函数单调性的判断:
在(-∝,1)上单调递增;在(2,+∝)单调递减.
合作探究
例7、求函数y=log2(x2+2x+17)的值域。
解:令u=x2+2x+17=(x+1)2+16≥16
又因为y=log2x是增函数,
所以,y=log2(x2+2x+17)=log2u
故y=log2(x2+2x+17)=log2u≥log216=4
所以,y=log2(x2+2x+17)的值域[4,+∝)
合作探究
我们观察函数y=2x与y=log2x 的图象关系,观察它们的图像:
在研究指数与对数时我们发现它们是密不可分的
那它们存在怎样的内存联系呢?
2
1
-1
-2
1
2
4
0
y
x
3
y=log2x
y=x
A ●
● A’
B ●
●
B’
y=2x
我们发现它们的图象关于直线y=x对称。
合作探究
再来观察
2
1
-1
-2
1
2
4
0
y
x
3
y=x
● B
●
B’
我们发现它们的图象也是关于直线y=x对称。
我们归纳得到结论:y=ax与y=logax图象关于直线y=x对称。
合作探究
反函数的定义
前面根据指数与对数间的关系,由 .由函数定义可知 是一个函数.这样,由指数函数 可得到对数函数 .这个对数函数的定义域 (0、1]值域
[0,+∞)分别是指数函数 的值域和定义域.
这时就说函数 是函数 的反函数.
像y=ax和x=logay 这样的两个函数叫作互为反函数.
通常情况下,用x 表示自变量, y表示函数,所以,指数函数y=ax 是对数函数 y=logax的反函数;同时,对数函数y=logax 是指数函数y=ax的反函数。
合作探究
例3:
写出下列函数的反函数:
(1) y=lgx (2) y=log0.5x
(3) y=5x (4) y=(0.8)x
解:
(1) y=10x
(2) y=(0.5)x
(3)
y=log5x
y=log0.8x
(4)
课堂练习
1、比较下列各组中,两个值的大小:
(1) Log23与 Log23.5 (2) Log 0.7 1.6与 Log 0.7 1.8
解1:考察函数y=log2 x ,
∵a=2 > 1, ∴函数在区间(0,+∞)上是增函数;
∵3<3.5 ∴ log23< log23.5
解2:考察函数y=log0.7 x ,
∵a=0.7< 1, ∴函数在区间(0,+∞)上是减函数;
∵1.6<1.8 ∴ log 0.7 1.6> log 0.7 1.8
课堂练习
2、求函数 的定义域.
解:
即
课堂练习
3、比较下列各组数字的大小
(1) log23.4>log28.5
(2) log0.31.8
当a>1时,
loga5.1
(5) 1.10.9>log0.70.8>log1.10.9
课堂总结
对数函数图像
y
X
O
x =1
(1,0)
y
X
O
x =1
(1,0)
对数函数性质
性 质 定义域 值域 特殊点 单调性
奇偶性
最值 (0,+ )
(0,+ )
R
R
过点(1,0)
过点(1,0)
在(0,+ )上是增函数
在(0,+ )上是减函数
非奇非偶函数
非奇非偶函数
无最值
无最值
a>1
0
对数函数图像
对数函数的性质
定义域
(0,+ )
值域
R
单调性
a>1
0
在(0,+ )上是减函数
性质的应用
作业布置
3、课本P135练习1、2、3
1、求函数y=loga(2x+1)-2 恒过的定点.
2、求函数 的单调区间及值域。
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
