必修 第一册5.1 任意角 课件(21张PPT)
文档属性
| 名称 | 必修 第一册5.1 任意角 课件(21张PPT) |

|
|
| 格式 | ppt | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 00:00:00 | ||
图片预览







文档简介
(共21张PPT)
太阳
地球
天体运动
现实世界中的许多运动、变化都有着循环往复、周而复始
的现象。
潮汐变化
三角函数
这种变化规律称之为周期性。刻画这种变化规律的数学模型
三角函数的起源
三角学的概念起源甚早,在古文献「来因德纸草书」出土后证据显示古埃及人己有实用三角学的粗略概念,来保持金字塔每边都有相同的斜度,只是当时并没有使用余切这个名词而已。至公元前150年至100年间,希腊人热衷天文学,开始研究三角学,于是三角学渐渐有了雏形。
后来,印度人吸收了希腊人在三角学方面的知识,再加以改进,也把它当成研究天文学的利器。长久以来,三角学就这样依附著天文学发展,直到十三世纪,才自天文学中脱离成一门独立的学问。十六世纪的欧洲,由于航海、历法计算的需要,更增加三角学的重要性。如今它不但应用于天文、地理,举凡航海、航空、建筑、工程、体育等…的一门基础学问,甚至在我们日常生活中,也成为不可欠缺的知识。
一、背景知识
任意角的三角函数是三角学中最基本最重要的概念之一。三角学起源于对三角形边角关系的研究,始于古希腊的喜帕恰斯、梅内劳斯和托勒密等人对天文的测量,在相当长的时期里隶属于天文学。直到1464年,德国数学家雷基奥蒙坦著《论各种三角形》,才独立于天文学之外对三角知识作了较系统的阐说;14~16世纪,三角学曾一度成为欧洲数学的主要内容,研究的方面包括三角函数值表的编制、平面三角形和球面三角形的解法,三角恒等式的建立和推导等等。1631年,三角学输入中国,三角学在中国早期比较通行的名称是“八线”和“三角”。“八线”是指在单位圆上的八种三角函数线:正弦线、余弦线、正切线、余切线、正割线、余割线、正矢线、余矢线。随着科学的发展,三角函数成为研究自然界和生产实践中周期变化现象的重要数学工具,它在测量、力学工程和无线电学中有着广泛的应用。
定义1:有公共端点的两条射线组成的几何图形叫做角。
三角函数
角
在初中,角是怎么定义的?
顶点
边
边
角的表示:
简记:
O
A
B
角的范围是什么:
o
A
B
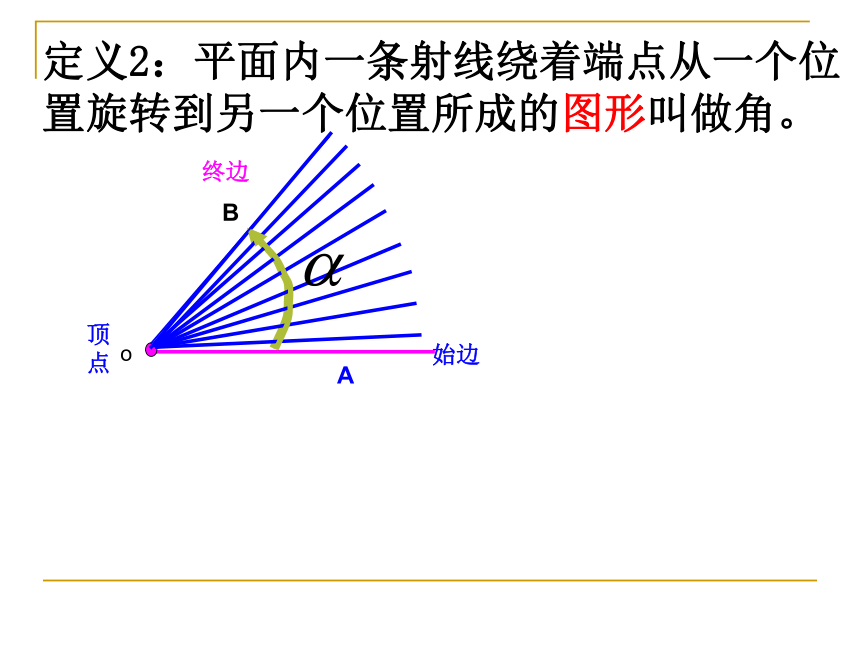
始边
终边
顶点
定义2:平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形叫做角。
体操运动员转体720 ,跳水运动员向内、向外转体1080
这些例子所提到的角不仅不在范围[00 ,3600 ] 中,而且还涉及到了方向,那么说明我们高中要研究的角的范围不应该局限于[00 ,3600 ],有必要将角的概念推广,那么如何将角进行推广呢?
举例
(1)如果你的手表慢了15分钟,你是如何将它校准的,
此时分针向什么方向旋转了几度?
(2)如果你的手表快了1个半小时,你是如何将它校准的,
此时分针向什么方向旋转了几度?
一.角的概念:
O
A
B
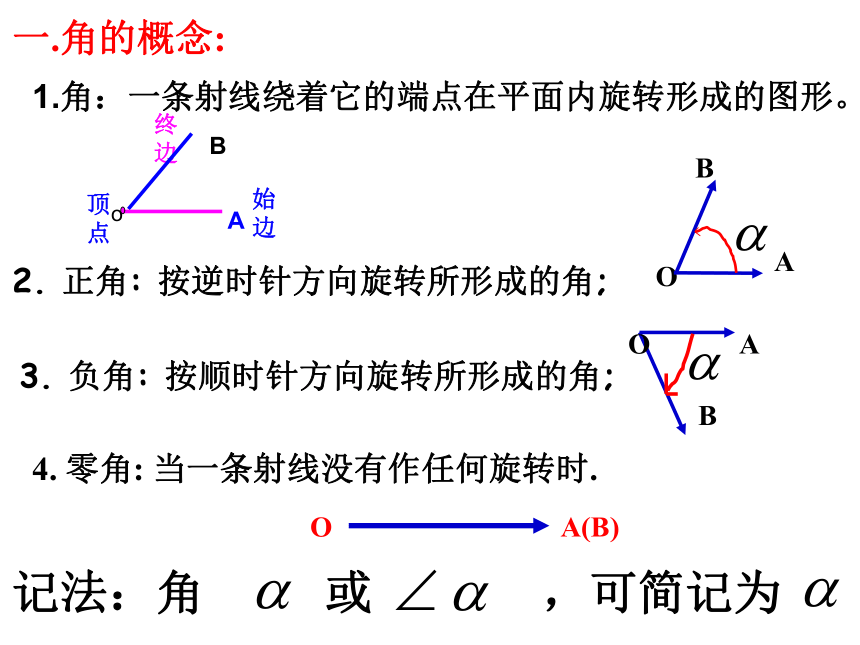
4. 零角: 当一条射线没有作任何旋转时.
O
A
B
O
A(B)
1.角:一条射线绕着它的端点在平面内旋转形成的图形。
2. 正角: 按逆时针方向旋转所形成的角;
3. 负角: 按顺时针方向旋转所形成的角;
o
A
B
始边
终边
顶点
记法:角 或 ,可简记为
思考下面的角度如何表示?
(1)你的手表慢了5分钟,想将它校准,分针应该旋转多少度?
(2)假如你的手表快了2.5小时,想将它校准,分针应该旋转多少度?
-30°
900°
注意:
1:角的正负由旋转方向决定。
2:角可以任意大小,绝对值大小由旋转次数及终边位置决定。
0
A
B
为了讨论问题的方便,我们使角的顶点与原点重合,
角的始边与x轴非负半轴重合。
O
A
B
0
x
y
此时终边落在第几象限就叫做第几象限角。
如果角的终边落在坐标轴上,就认为这个角不属于任何
一个象限。
这样的角称为轴线角(或轴上角)
象限角
例如:角的终边落在X轴或Y轴上。
练习:在直角坐标系内画出下列各角,
并判断下列各角分别属于哪个象限?
(1)120°(2)-135°(3)280°(4)390°
问题:1.锐角一定是第一象限角
4.00~900的角一定是锐角
3.小于900的角一定是锐角
2.第一象限角一定是锐角
(说明:00~900是 的意思)
想一想
问题一:20°角与 380°角的终边有关系吗?
如果不唯一,那么这些相同终边的角
有什么关系?
(它们正好相差整数圈)
0
x
y
200
B
如图所示,如果一个角 的终边落在
OB上,那么这个角是否唯一?
问题二:
你能否继续给出与200 角终边相同的角。
所有与角α终边相同的角,连同角α在内,可构成一个集合
S={β|β=α+k 360。K Z}
想一想
如果角 与角 终边相同,那么它们
应该满足什么关系?
问题三:
注:(1) K ∈ Z
(2) 是任意角
(3)K·360°与 之间是“+”号,如K·360°-30 °,应看成K·360 °+(-30 ° )
(4)终边相同的角不一定相等,但相等的角终边一定相同,终边相同的角有无数多个,它们相差360°的整数倍
终边相同的角一定相等吗?相等的角终边一定相同吗?
练一练.下列各命题:
(1)相等的角终边一定相同;
(2)终边相同的角一定相等;
(3)第二象限的角一定大于第一象限任意一个角;
(4)若 ,则 必是第一或第二象限角
其中正确的有几个?
例1.在00~3600间,找出与下列各角终边
相同的角,并判断它们是第几象限角
-1200
P5 练习4
(2) 6600
(3) -950008/
把上题(1)中 适合不等式-3600≤ <7200
的元素 写出来
归纳出特殊位置的角的集合的方法步骤:
例4.写出终边在y轴上的角的集合(用00至3600角表示)
变式:写出终边在x轴上的角的集合(用00至3600角表示)
2.写出与上述角终边相同的角的集合。
1.在00至3600范围内找到特殊位置的角。
3.写出几个集合的并集(若有可能化简,则化为最简形式)。
例5.写出终边在直线y=x上的角的集合S,并把集合中
适合不等式 的元素 找出来?
有关角的概念的推广及分类
太阳
地球
天体运动
现实世界中的许多运动、变化都有着循环往复、周而复始
的现象。
潮汐变化
三角函数
这种变化规律称之为周期性。刻画这种变化规律的数学模型
三角函数的起源
三角学的概念起源甚早,在古文献「来因德纸草书」出土后证据显示古埃及人己有实用三角学的粗略概念,来保持金字塔每边都有相同的斜度,只是当时并没有使用余切这个名词而已。至公元前150年至100年间,希腊人热衷天文学,开始研究三角学,于是三角学渐渐有了雏形。
后来,印度人吸收了希腊人在三角学方面的知识,再加以改进,也把它当成研究天文学的利器。长久以来,三角学就这样依附著天文学发展,直到十三世纪,才自天文学中脱离成一门独立的学问。十六世纪的欧洲,由于航海、历法计算的需要,更增加三角学的重要性。如今它不但应用于天文、地理,举凡航海、航空、建筑、工程、体育等…的一门基础学问,甚至在我们日常生活中,也成为不可欠缺的知识。
一、背景知识
任意角的三角函数是三角学中最基本最重要的概念之一。三角学起源于对三角形边角关系的研究,始于古希腊的喜帕恰斯、梅内劳斯和托勒密等人对天文的测量,在相当长的时期里隶属于天文学。直到1464年,德国数学家雷基奥蒙坦著《论各种三角形》,才独立于天文学之外对三角知识作了较系统的阐说;14~16世纪,三角学曾一度成为欧洲数学的主要内容,研究的方面包括三角函数值表的编制、平面三角形和球面三角形的解法,三角恒等式的建立和推导等等。1631年,三角学输入中国,三角学在中国早期比较通行的名称是“八线”和“三角”。“八线”是指在单位圆上的八种三角函数线:正弦线、余弦线、正切线、余切线、正割线、余割线、正矢线、余矢线。随着科学的发展,三角函数成为研究自然界和生产实践中周期变化现象的重要数学工具,它在测量、力学工程和无线电学中有着广泛的应用。
定义1:有公共端点的两条射线组成的几何图形叫做角。
三角函数
角
在初中,角是怎么定义的?
顶点
边
边
角的表示:
简记:
O
A
B
角的范围是什么:
o
A
B
始边
终边
顶点
定义2:平面内一条射线绕着端点从一个位置旋转到另一个位置所成的图形叫做角。
体操运动员转体720 ,跳水运动员向内、向外转体1080
这些例子所提到的角不仅不在范围[00 ,3600 ] 中,而且还涉及到了方向,那么说明我们高中要研究的角的范围不应该局限于[00 ,3600 ],有必要将角的概念推广,那么如何将角进行推广呢?
举例
(1)如果你的手表慢了15分钟,你是如何将它校准的,
此时分针向什么方向旋转了几度?
(2)如果你的手表快了1个半小时,你是如何将它校准的,
此时分针向什么方向旋转了几度?
一.角的概念:
O
A
B
4. 零角: 当一条射线没有作任何旋转时.
O
A
B
O
A(B)
1.角:一条射线绕着它的端点在平面内旋转形成的图形。
2. 正角: 按逆时针方向旋转所形成的角;
3. 负角: 按顺时针方向旋转所形成的角;
o
A
B
始边
终边
顶点
记法:角 或 ,可简记为
思考下面的角度如何表示?
(1)你的手表慢了5分钟,想将它校准,分针应该旋转多少度?
(2)假如你的手表快了2.5小时,想将它校准,分针应该旋转多少度?
-30°
900°
注意:
1:角的正负由旋转方向决定。
2:角可以任意大小,绝对值大小由旋转次数及终边位置决定。
0
A
B
为了讨论问题的方便,我们使角的顶点与原点重合,
角的始边与x轴非负半轴重合。
O
A
B
0
x
y
此时终边落在第几象限就叫做第几象限角。
如果角的终边落在坐标轴上,就认为这个角不属于任何
一个象限。
这样的角称为轴线角(或轴上角)
象限角
例如:角的终边落在X轴或Y轴上。
练习:在直角坐标系内画出下列各角,
并判断下列各角分别属于哪个象限?
(1)120°(2)-135°(3)280°(4)390°
问题:1.锐角一定是第一象限角
4.00~900的角一定是锐角
3.小于900的角一定是锐角
2.第一象限角一定是锐角
(说明:00~900是 的意思)
想一想
问题一:20°角与 380°角的终边有关系吗?
如果不唯一,那么这些相同终边的角
有什么关系?
(它们正好相差整数圈)
0
x
y
200
B
如图所示,如果一个角 的终边落在
OB上,那么这个角是否唯一?
问题二:
你能否继续给出与200 角终边相同的角。
所有与角α终边相同的角,连同角α在内,可构成一个集合
S={β|β=α+k 360。K Z}
想一想
如果角 与角 终边相同,那么它们
应该满足什么关系?
问题三:
注:(1) K ∈ Z
(2) 是任意角
(3)K·360°与 之间是“+”号,如K·360°-30 °,应看成K·360 °+(-30 ° )
(4)终边相同的角不一定相等,但相等的角终边一定相同,终边相同的角有无数多个,它们相差360°的整数倍
终边相同的角一定相等吗?相等的角终边一定相同吗?
练一练.下列各命题:
(1)相等的角终边一定相同;
(2)终边相同的角一定相等;
(3)第二象限的角一定大于第一象限任意一个角;
(4)若 ,则 必是第一或第二象限角
其中正确的有几个?
例1.在00~3600间,找出与下列各角终边
相同的角,并判断它们是第几象限角
-1200
P5 练习4
(2) 6600
(3) -950008/
把上题(1)中 适合不等式-3600≤ <7200
的元素 写出来
归纳出特殊位置的角的集合的方法步骤:
例4.写出终边在y轴上的角的集合(用00至3600角表示)
变式:写出终边在x轴上的角的集合(用00至3600角表示)
2.写出与上述角终边相同的角的集合。
1.在00至3600范围内找到特殊位置的角。
3.写出几个集合的并集(若有可能化简,则化为最简形式)。
例5.写出终边在直线y=x上的角的集合S,并把集合中
适合不等式 的元素 找出来?
有关角的概念的推广及分类
同课章节目录
- 第一章 集合与常用逻辑用语
- 1.1 集合的概念
- 1.2 集合间的基本关系
- 1.3 集合的基本运算
- 1.4 充分条件与必要条件
- 1.5 全称量词与存在量词
- 第二章 一元二次函数、方程和不等式
- 2.1 等式性质与不等式性质
- 2.2 基本不等式
- 2.3 二次函数与一元二次方程、不等式
- 第三章 函数概念与性质
- 3.1 函数的概念及其表示
- 3.2 函数的基本性质
- 3.3 幂函数
- 3.4 函数的应用(一)
- 第四章 指数函数与对数函数
- 4.1 指数
- 4.2 指数函数
- 4.3 对数
- 4.4 对数函数
- 4.5 函数的应用(二)
- 第五章 三角函数
- 5.1 任意角和弧度制
- 5.2 三角函数的概念
- 5.3 诱导公式
- 5.4 三角函数的图象与性质
- 5.5 三角恒等变换
- 5.6 函数 y=Asin( ωx + φ)
- 5.7 三角函数的应用
