选择性必修 第一册 3.1.1 椭圆的标准方程 课件(21张PPT)
文档属性
| 名称 | 选择性必修 第一册 3.1.1 椭圆的标准方程 课件(21张PPT) |  | |
| 格式 | ppt | ||
| 文件大小 | 881.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教A版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 15:21:59 | ||
图片预览






文档简介
(共24张PPT)
生活中你还见过椭圆形状的物品吗?
地球绕着太阳旋转的轨迹是什么?
生活中的椭圆
1.问题情境
如何精确地设计、制作、建造出现实生活中这些椭圆形的物件呢?
[1]取一条细绳,
[2]把它的两端固定在白纸上的两点F1、F2
[3]用圆珠笔尖(M)把细绳拉紧,在白纸上慢慢移动,画出的图形是什么
F1
F2
[1]取一条细绳,
[2]把它的两端固定在白纸上的两点F1、F2
[3]用圆珠笔尖(M)把细绳拉紧,在白纸上慢慢移动,画出的图形是什么
椭圆的定义:
F1
F2
M
2c
平面内与两个定点F1、F2的距离的和等于常数
(大于|F1F2|)的点的轨迹叫做椭圆。
这两个定点F1、F2叫做椭圆的焦点,两焦点的
距离叫做椭圆焦距。
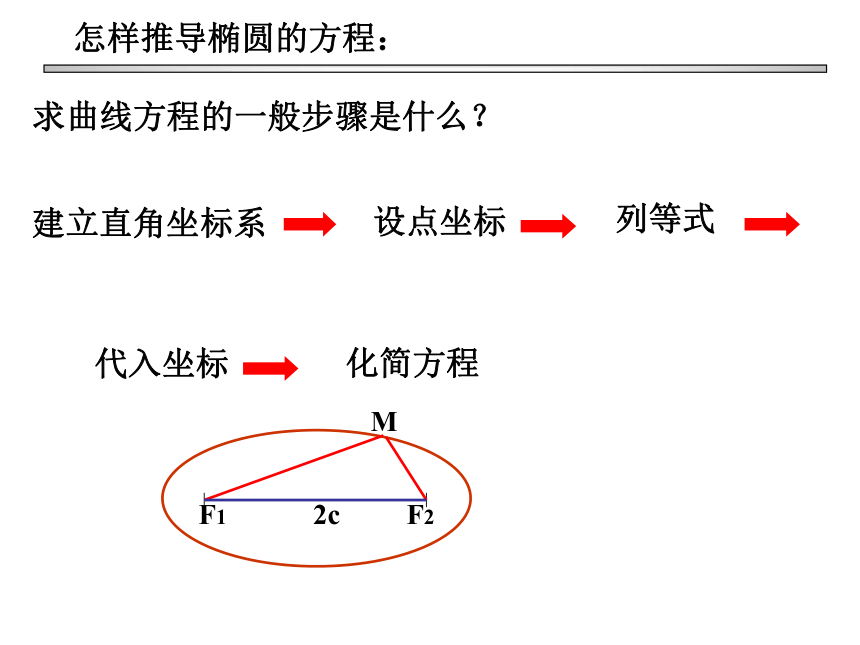
怎样推导椭圆的方程:
建立直角坐标系
列等式
设点坐标
代入坐标
化简方程
求曲线方程的一般步骤是什么?
F1
F2
M
2c
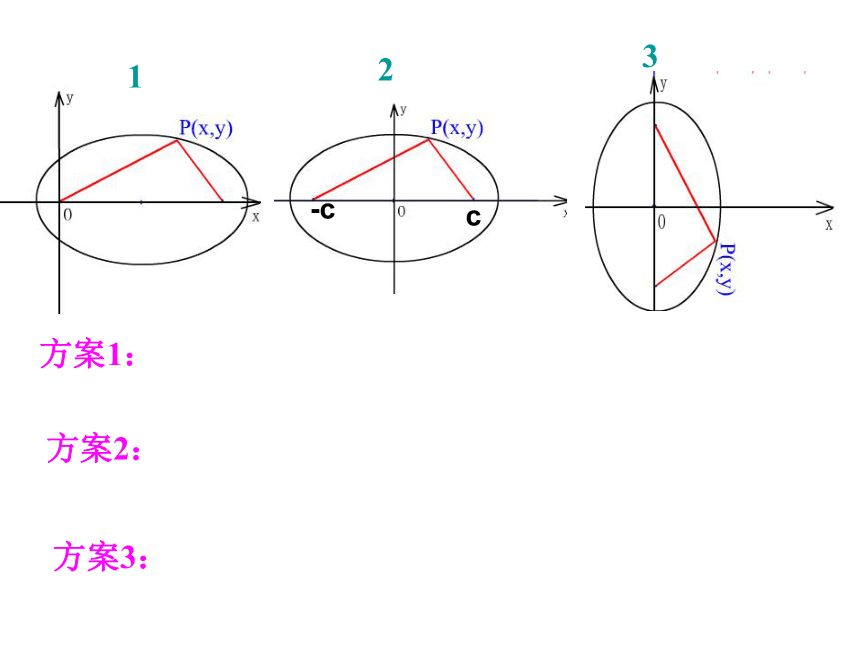
1
2
3
方案1:
方案2:
方案3:
-c
c
1
2
3
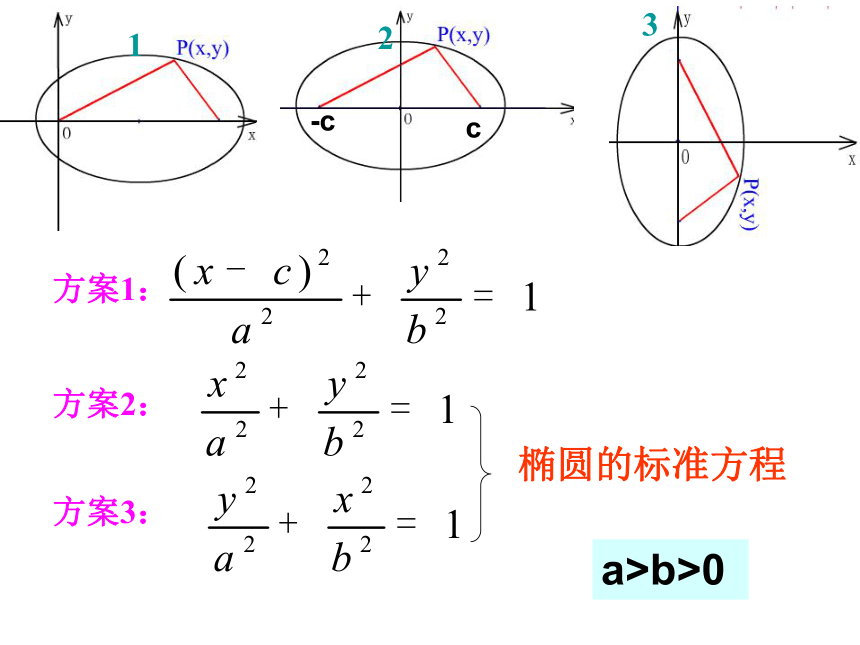
方案1:
方案2:
方案3:
椭圆的标准方程
a>b>0
-c
c
焦点位置判定
1
2
y
o
F
F
M
x
y
x
o
F
2
F
1
M
定 义
图 形
方 程
焦 点
F(±c,0)
F(0,±c)
a,b,c之间的关系
|MF1|+|MF2|=2a (2a>2c>0)
椭圆的标准方程
B
B
a2=c2+b2 ,
课堂练习
已知椭圆的方程为: ,请填空:
(1) a=__,b=__,c=__,焦点坐标为___________,焦距等于__.
(2)若P为椭圆上一点,F1、F2分别为椭圆的左、右焦点,
并且PF1=6,则PF2=___.
10
6
8
16
(-8,0)、(8,0)
14
x
y
0
P
F1
F2
x
y
0
F1
F2
C
D
36
40
课堂练习
变题: 若椭圆的方程为 ,求a,b,c.
若方程 ①表示焦点在y轴上的椭圆,
求k的取值范围;
思考:
②若方程表示椭圆呢
例2:求适合下列条件的椭圆的标准方程
两个焦点的坐标分别是(-4,0),(4,0)
椭圆上一点P到两焦点距离的和等于10
(3)两个焦点的坐标分别是(0,-2),(0,2)
并且椭圆经过点
例3.已知
是该椭圆上两点,
点坐标为
,
,且
求这椭圆的标准方程.
例4.已知椭圆
,焦点为
、
,
是椭圆上一点,且
求
的面积。
一、二、三
一个概念;
二个方程;
三个意识:严谨意识,
求美意识,
求简意识。
|MF1|+|MF2|=2a(2a>2c>0)
生活中你还见过椭圆形状的物品吗?
地球绕着太阳旋转的轨迹是什么?
生活中的椭圆
1.问题情境
如何精确地设计、制作、建造出现实生活中这些椭圆形的物件呢?
[1]取一条细绳,
[2]把它的两端固定在白纸上的两点F1、F2
[3]用圆珠笔尖(M)把细绳拉紧,在白纸上慢慢移动,画出的图形是什么
F1
F2
[1]取一条细绳,
[2]把它的两端固定在白纸上的两点F1、F2
[3]用圆珠笔尖(M)把细绳拉紧,在白纸上慢慢移动,画出的图形是什么
椭圆的定义:
F1
F2
M
2c
平面内与两个定点F1、F2的距离的和等于常数
(大于|F1F2|)的点的轨迹叫做椭圆。
这两个定点F1、F2叫做椭圆的焦点,两焦点的
距离叫做椭圆焦距。
怎样推导椭圆的方程:
建立直角坐标系
列等式
设点坐标
代入坐标
化简方程
求曲线方程的一般步骤是什么?
F1
F2
M
2c
1
2
3
方案1:
方案2:
方案3:
-c
c
1
2
3
方案1:
方案2:
方案3:
椭圆的标准方程
a>b>0
-c
c
焦点位置判定
1
2
y
o
F
F
M
x
y
x
o
F
2
F
1
M
定 义
图 形
方 程
焦 点
F(±c,0)
F(0,±c)
a,b,c之间的关系
|MF1|+|MF2|=2a (2a>2c>0)
椭圆的标准方程
B
B
a2=c2+b2 ,
课堂练习
已知椭圆的方程为: ,请填空:
(1) a=__,b=__,c=__,焦点坐标为___________,焦距等于__.
(2)若P为椭圆上一点,F1、F2分别为椭圆的左、右焦点,
并且PF1=6,则PF2=___.
10
6
8
16
(-8,0)、(8,0)
14
x
y
0
P
F1
F2
x
y
0
F1
F2
C
D
36
40
课堂练习
变题: 若椭圆的方程为 ,求a,b,c.
若方程 ①表示焦点在y轴上的椭圆,
求k的取值范围;
思考:
②若方程表示椭圆呢
例2:求适合下列条件的椭圆的标准方程
两个焦点的坐标分别是(-4,0),(4,0)
椭圆上一点P到两焦点距离的和等于10
(3)两个焦点的坐标分别是(0,-2),(0,2)
并且椭圆经过点
例3.已知
是该椭圆上两点,
点坐标为
,
,且
求这椭圆的标准方程.
例4.已知椭圆
,焦点为
、
,
是椭圆上一点,且
求
的面积。
一、二、三
一个概念;
二个方程;
三个意识:严谨意识,
求美意识,
求简意识。
|MF1|+|MF2|=2a(2a>2c>0)
