探寻破解数列不等式 “三重门”的策略(共72张PPT)
文档属性
| 名称 | 探寻破解数列不等式 “三重门”的策略(共72张PPT) |  | |
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 16:09:36 | ||
图片预览










文档简介
(共72张PPT)
有的放矢 精确把握
---探寻破解数列不等式 “三重门”的策略
龙游县第二高级中学 陈宣新
二O一八年三月二十三日
新高考考试说明
1.了解数列的概念和几种表示方法。(列表、图象、通项公式)
2.理解等差数列、等比数列的概念,掌握等差数列、等比数列的通项公式与前n项和公式。
3.了解等差数列与一次函数、等比数列与指数函数的关系。
4.会用数列的等差关系或等比关系解决实际问题。
5.会用数学归纳法证明一些简单数学问题(新增)
新旧高考总体变化不大
有必要对近几年高考数列部分作研究分析
提醒:
**.知识关系:理解数列和函数的关系.
**.知识交汇:数列与函数、导数、不等式有关的知识.
**.方 法:数学归纳法,导数法,放缩法等.
一、研析近三年高考数列大题
2015浙江高考题:
压轴题
2015年浙江20解析
颠倒\裂项\求和\放缩
一、研析近三年高考数列大题
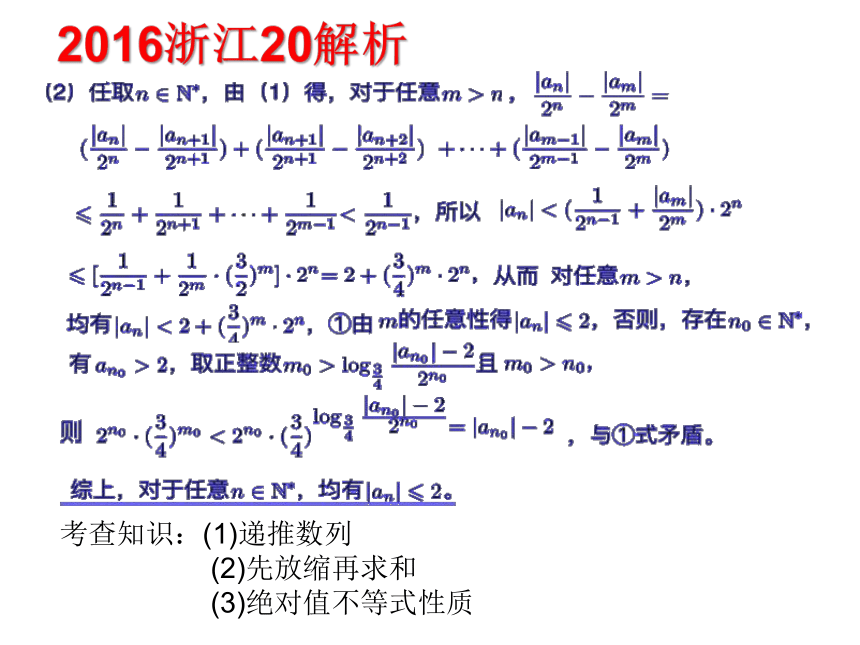
2016浙江高考题:
又是压轴题
考查知识:(1)递推数列
(2)先放缩再求和
(3)绝对值不等式性质
2016浙江20解析
2017浙江高考22题
.
还是压轴题
2017浙江高考22题(2)小题
知识:函数不等式与数列不等式。
2017浙江高考22题(3)小题
数列压轴题“压”在哪里?
三年压轴题比较:前两年和不等式结合紧密;2017年22题是函数导数背景下的数列不等式。
三大关(三重门):知识跨度大,解题思路窄,计算技巧穷
是我们想突破的“三重门”
结合近三年的数列高考题,预测今年还是以稳定为主还是以选择+大题或填空+大题,分值为20分左右。考查内容以等差等比数列性质、递推数列求通项、放缩法求和、与函数不等式相结合的应用等。就数列来说,就接下来数列的复习,一个是要抓基础,另一方面要破难点。结合学生的疑惑和课堂中的问题,今天想关注以下四个方面,也是中等学生经常有的困惑.
困惑一:放缩法怎么把握的“度”
困惑二:错位相减法老是要算错,怎么办?
困惑三:教材重要吗,习题及以往考题呢?
困惑四:如何从函数不等式到数列不等式的过渡?
…….
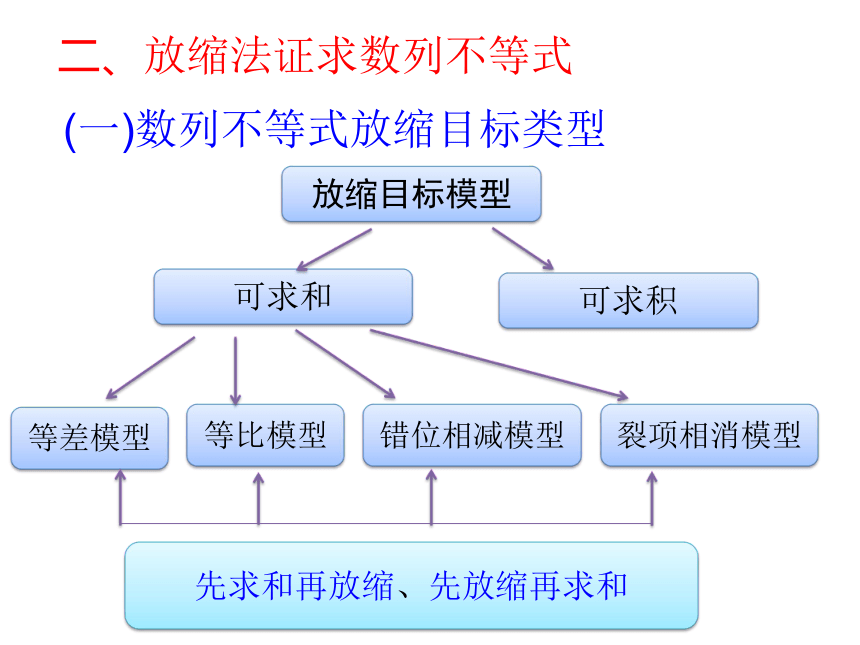
(一)数列不等式放缩目标类型
二、放缩法证求数列不等式
放缩目标模型
可求和
可求积
等差模型
等比模型
错位相减模型
裂项相消模型
先求和再放缩、先放缩再求和
(一)数列不等式放缩目标类型
二、放缩法证求数列不等式
1.等差模型
证明∵
∴
(一)几种数列放缩模型
例1:
2.等比模型
左边
∵
∴
当n = 1时,不等式显然也成立.
此外还有错位相减模型、裂项相消模型等。
例2:
(一)几种数列放缩模型
(二)探寻数列不等式放缩的 “度”
学生困惑:
(1)“放大一点点则太大,缩小一点点则太小”。
(2)“前一项开始放缩不行,后一项放缩也不行”?许多学生很茫然,找不到头绪,摸不着规律,觉得高不可攀!
解决问题建议:
“对症下药以”----探寻数列不等式放缩 “度”和 “项”为抓手,总结一常用的放缩处理方法。
例3:【2013广东理】
(二)探究裂项型放缩 的“度”
(二)探究裂项型放缩 的“度”
(二)探究裂项型放缩 的“度”
放缩“度”:<<
(二)探究裂项型放缩 的“度”
1.探究裂而不消问题
(二)探究裂项型放缩 的“度”
1.裂而不消问题
变式:
解析1:
(二)探究裂项型放缩 的“度”
2.探究“放缩度与放缩项”的关系
小结:用
放缩要保留前五项,从第六项放缩,计算繁琐。
(二)探究裂项型放缩 的“度”
2.探究“放缩度与放缩项”的关系
变式:
解析2:
(二)探究裂项型放缩 的“度”
2.探究“放缩度与放缩项”的关系
变式:
(二)探究裂项型放缩 的“度”
2.探究“放缩度与放缩项”的关系
要从第8项开始放缩
只要从第2项开始放缩
(二)探究裂项型放缩 的“度”
2.探究“放缩度与放缩项”的关系
要把握好放缩法可以从两个方面考虑:
1.通项放缩程度。
2.调整放缩的第一项。
1.方法小结:
2.常见的裂项
平方型:
(二)探究裂项型放缩 的“度”
立方型:
根式型:
以上几种类型都可以化为裂项型放缩
(二)探究裂项型放缩 的“度
思路:利用指数函数的单调性放缩为等比模型
左边
∵
∴
(2012广东理19题)
(三)探究等比型放缩 的“度”
(2012广东理19题变式)
(三)探究等比型放缩 的“度”
指数型:
(三)探究等比型放缩 的“度”小结
1.(08·辽宁卷)已知:
求证: .
故
当 时,有 也成立.
(四)高考题或模拟高考题赏析
4.(2018年1月台州统测22题)
(2)通项分析:
(四)高考题或模拟高考题赏析
(四)高考题或模拟高考题赏析
4.(2018年1月台州统测22题)
解:(2)
{an·bn}(其中{an是公差为d(d≠0)的等差数列,{bn}是公比为q(q≠1)的等比数列)型的数列前n项的和Sn的方法—错位相减法. “错位相减”是推导等比数列前n项和公式的核心技术,并由此出发得到了求形如 长期以来,人们对求形如{an·bn}型的数列前n项的和不仅常用“错位相减法”求解,而且“错位相减法”也是历年高考命题的热点。
然而,在平时的练习和历年高考中,我们发现用 “错位相减法”求这类数列的和,学生们不仅感到厌烦,而且错误率颇高。那么有没有其它方法可以替代“错位相减法” 来求这类数列的和,从而减少错误率 下面我们还是从推导等比数列前项和公式谈起.
三.差比数列一定用错位相减吗?
裂项相消法
三、探究差比数列求和
1.从前n项和的角度分析
2.从通项公式的角度分析
三、探究差比数列求和
裂项相消法
思考:=(2
用裂项相消
降低运算量
化解难点
三、探究差比数列求和
(2012辽宁理)
分析:“错位相减法”求“差比型”数列的和有固定的求解模式,但计算量大,易出错。经过学生的测试,用裂项相消法的大大节省时间和提高准确率。
三、探究差比数列求和
(2012辽宁理)
[ 2013山东理 ]
二、探究差比数列求和
解:(1)=2n-1
(2)=-
===
=,得A=
=
++…+= -
解法1:裂项相消法
解法2:待定系数法
解法3:函数导数法分析
解法3:函数导数法
解法4:待定系数法
事实上,差比数列是一种特殊的函数,我们若能注意灵活运用函数的思想方法来处理数列问题不仅能拓宽解题的视野,提高解题效率,而且对于培养学生的数学思维能力大有裨益。
四:分析考题寻根源,回归教材研真题
纵观近几年高考数列题,大都着重围绕等差数列与等比数列大做文章,要重视“通性通法”、注重基础知识、注重核心概念、倡导回归本源。
目前的实际情况,高三复习课往往所用的资料各类教辅用书代替教材,用做题目代替一切。其实就,高考考题分析,越来越重视教材、重视知识的形成过程、重视高考真的研读。命题专家重视教材作用,发挥教材功能,在命题手法上,常通过教材上例题、习题等题目的改造、移植、嫁接等,编制出立意深远、背景丰富、表述简洁的新题。这就提醒我们要重视教材的作用,强化解题基本功。
分析:教材中推导等比数列前 项和的方法是错位相减法,此种方法虽然是一种典型的处理数列的方法,但学生也很难达到十分熟练的程度,错位相减法的数列求和中的地位又是相当重要的,所以通过公式的推导让学生思维上回归到书本。
(一)回归教材,注重知识形成
以上过程的相反过程就是裂项相消法,这样的教学过程既巩固了裂项相消法,又训练了学生的逆向思维能力。(可用分析法证明)
小结:回归课本将公式进行推导不是一种简单的重复,而是对数学思想、解题方法在学生心中的一种重塑,一种唤醒的方式。这样一方面能使知识得到复习,另一方面也不用通过大量的题目来得到或回顾上面的几种求和的方法,是真正意义上的二轮复习。
(湖南2012,第21题)
(人教A版必修5第76页,第11题)
(二)回归教材,挖掘习题功能
(2015陕西,第21题)
(人教版A必修五第69页习题第4题(3))
分析:(1)先求和再求导最后令x=2得出结论。
也可以先求导再求和最后令x=2得出结论。
(三)考题“重现” 注重类比分析
(17浙江卷,22题)
[06年浙江卷,22题]
再现考题
说明:2017年2题第(3)小题与2006年22题第(2)小题证明的是同一个结论.06年的题直接从导数的儿何意义出发设计问题,而17年的题隐去了导数的儿何意义,需要考生去挖掘,对考生的数学能力来说是挑战。由此可见关注以往的高考考题是有必要的。
(三)考题“重现” 注重类比分析
(17浙江卷,21题)
(08浙江卷,20题)
(三)考题重现,注重类比分析
(三)考题“重现” 注重类比分析
除了以上所列举的,其实2017年的浙江卷第7题由2007年理科卷第8题改编而来;第15题由2014年理科卷第8题改编而来;第17题由2008年理科卷第15题改编而来;
高考试题源于课本与以往的高考题,至少有两个理由:
1. 命题设计尽可能地从现实问题或熟悉背景出发,构造出素材朴实、内蕴丰富的试题,充分体现数学的内在实质试卷中的题目处处闪现着问题解决的智慧。
2.同时也是高考公平性的体现。这样可以很好的引导教师、学生避兔将大量的精力消耗在盲目套所谓技巧上,只要会思考、具有良好思维品质就能考出优异成绩。
(三)考题“重现” 注重类比分析
函数导数与数列型不等式的交汇问题,体现了导数的工具性,凸显了知识之间的纵横联系,一些题构思精巧、新颖,加强对能力的考察,逐渐成为高考的新亮点。2017年浙江22题就是这样的问题。
2017浙江高考22题
四. 考题三研读---重视函数背景下的数列不等式
三现考题
四. 考题三研读---重视函数背景下的数列不等式
评注: 从上面的解答方法可以看出,解决问题的方法为由函数得到函数不等式,进而对x取值,再得到数列不等式,达到解决问题的目的。在此过程中有两个关键步骤:其一是如何得到函数不等式;其二是如何由函数不等式过渡到数列不等式
四. 考题三研读---重视函数背景下的数列不等式
例如:
四. 考题三研读---重视函数背景下的数列不等式
四. 考题三研读---重视函数背景下的数列不等式
四. 考题三研读---重视函数背景下的数列不等式
下面我们一起看看2018年各地市的模拟考试题
四. 考题三研读---重视函数背景下的数列不等式
(2017年9月湖衢丽统测卷22题)
四. 从函数不等式到数列不等式
(2018年1月湖衢丽统测卷22题)
四. 从函数不等式到数列不等式
(2018年1月湖衢丽统测卷22题)
四. 从函数不等式到数列不等式
4.(2018年1月台州统测22题)
四. 从函数不等式到数列不等式
方法小结:
构造函数
函数不等式
数列不等式
放缩和求和
解决问题
二轮复习建议:
了解学情,有的放矢.回归教材,研究考题
谢谢各位专家同仁
有的放矢 精确把握
---探寻破解数列不等式 “三重门”的策略
龙游县第二高级中学 陈宣新
二O一八年三月二十三日
新高考考试说明
1.了解数列的概念和几种表示方法。(列表、图象、通项公式)
2.理解等差数列、等比数列的概念,掌握等差数列、等比数列的通项公式与前n项和公式。
3.了解等差数列与一次函数、等比数列与指数函数的关系。
4.会用数列的等差关系或等比关系解决实际问题。
5.会用数学归纳法证明一些简单数学问题(新增)
新旧高考总体变化不大
有必要对近几年高考数列部分作研究分析
提醒:
**.知识关系:理解数列和函数的关系.
**.知识交汇:数列与函数、导数、不等式有关的知识.
**.方 法:数学归纳法,导数法,放缩法等.
一、研析近三年高考数列大题
2015浙江高考题:
压轴题
2015年浙江20解析
颠倒\裂项\求和\放缩
一、研析近三年高考数列大题
2016浙江高考题:
又是压轴题
考查知识:(1)递推数列
(2)先放缩再求和
(3)绝对值不等式性质
2016浙江20解析
2017浙江高考22题
.
还是压轴题
2017浙江高考22题(2)小题
知识:函数不等式与数列不等式。
2017浙江高考22题(3)小题
数列压轴题“压”在哪里?
三年压轴题比较:前两年和不等式结合紧密;2017年22题是函数导数背景下的数列不等式。
三大关(三重门):知识跨度大,解题思路窄,计算技巧穷
是我们想突破的“三重门”
结合近三年的数列高考题,预测今年还是以稳定为主还是以选择+大题或填空+大题,分值为20分左右。考查内容以等差等比数列性质、递推数列求通项、放缩法求和、与函数不等式相结合的应用等。就数列来说,就接下来数列的复习,一个是要抓基础,另一方面要破难点。结合学生的疑惑和课堂中的问题,今天想关注以下四个方面,也是中等学生经常有的困惑.
困惑一:放缩法怎么把握的“度”
困惑二:错位相减法老是要算错,怎么办?
困惑三:教材重要吗,习题及以往考题呢?
困惑四:如何从函数不等式到数列不等式的过渡?
…….
(一)数列不等式放缩目标类型
二、放缩法证求数列不等式
放缩目标模型
可求和
可求积
等差模型
等比模型
错位相减模型
裂项相消模型
先求和再放缩、先放缩再求和
(一)数列不等式放缩目标类型
二、放缩法证求数列不等式
1.等差模型
证明∵
∴
(一)几种数列放缩模型
例1:
2.等比模型
左边
∵
∴
当n = 1时,不等式显然也成立.
此外还有错位相减模型、裂项相消模型等。
例2:
(一)几种数列放缩模型
(二)探寻数列不等式放缩的 “度”
学生困惑:
(1)“放大一点点则太大,缩小一点点则太小”。
(2)“前一项开始放缩不行,后一项放缩也不行”?许多学生很茫然,找不到头绪,摸不着规律,觉得高不可攀!
解决问题建议:
“对症下药以”----探寻数列不等式放缩 “度”和 “项”为抓手,总结一常用的放缩处理方法。
例3:【2013广东理】
(二)探究裂项型放缩 的“度”
(二)探究裂项型放缩 的“度”
(二)探究裂项型放缩 的“度”
放缩“度”:<<
(二)探究裂项型放缩 的“度”
1.探究裂而不消问题
(二)探究裂项型放缩 的“度”
1.裂而不消问题
变式:
解析1:
(二)探究裂项型放缩 的“度”
2.探究“放缩度与放缩项”的关系
小结:用
放缩要保留前五项,从第六项放缩,计算繁琐。
(二)探究裂项型放缩 的“度”
2.探究“放缩度与放缩项”的关系
变式:
解析2:
(二)探究裂项型放缩 的“度”
2.探究“放缩度与放缩项”的关系
变式:
(二)探究裂项型放缩 的“度”
2.探究“放缩度与放缩项”的关系
要从第8项开始放缩
只要从第2项开始放缩
(二)探究裂项型放缩 的“度”
2.探究“放缩度与放缩项”的关系
要把握好放缩法可以从两个方面考虑:
1.通项放缩程度。
2.调整放缩的第一项。
1.方法小结:
2.常见的裂项
平方型:
(二)探究裂项型放缩 的“度”
立方型:
根式型:
以上几种类型都可以化为裂项型放缩
(二)探究裂项型放缩 的“度
思路:利用指数函数的单调性放缩为等比模型
左边
∵
∴
(2012广东理19题)
(三)探究等比型放缩 的“度”
(2012广东理19题变式)
(三)探究等比型放缩 的“度”
指数型:
(三)探究等比型放缩 的“度”小结
1.(08·辽宁卷)已知:
求证: .
故
当 时,有 也成立.
(四)高考题或模拟高考题赏析
4.(2018年1月台州统测22题)
(2)通项分析:
(四)高考题或模拟高考题赏析
(四)高考题或模拟高考题赏析
4.(2018年1月台州统测22题)
解:(2)
{an·bn}(其中{an是公差为d(d≠0)的等差数列,{bn}是公比为q(q≠1)的等比数列)型的数列前n项的和Sn的方法—错位相减法. “错位相减”是推导等比数列前n项和公式的核心技术,并由此出发得到了求形如 长期以来,人们对求形如{an·bn}型的数列前n项的和不仅常用“错位相减法”求解,而且“错位相减法”也是历年高考命题的热点。
然而,在平时的练习和历年高考中,我们发现用 “错位相减法”求这类数列的和,学生们不仅感到厌烦,而且错误率颇高。那么有没有其它方法可以替代“错位相减法” 来求这类数列的和,从而减少错误率 下面我们还是从推导等比数列前项和公式谈起.
三.差比数列一定用错位相减吗?
裂项相消法
三、探究差比数列求和
1.从前n项和的角度分析
2.从通项公式的角度分析
三、探究差比数列求和
裂项相消法
思考:=(2
用裂项相消
降低运算量
化解难点
三、探究差比数列求和
(2012辽宁理)
分析:“错位相减法”求“差比型”数列的和有固定的求解模式,但计算量大,易出错。经过学生的测试,用裂项相消法的大大节省时间和提高准确率。
三、探究差比数列求和
(2012辽宁理)
[ 2013山东理 ]
二、探究差比数列求和
解:(1)=2n-1
(2)=-
===
=,得A=
=
++…+= -
解法1:裂项相消法
解法2:待定系数法
解法3:函数导数法分析
解法3:函数导数法
解法4:待定系数法
事实上,差比数列是一种特殊的函数,我们若能注意灵活运用函数的思想方法来处理数列问题不仅能拓宽解题的视野,提高解题效率,而且对于培养学生的数学思维能力大有裨益。
四:分析考题寻根源,回归教材研真题
纵观近几年高考数列题,大都着重围绕等差数列与等比数列大做文章,要重视“通性通法”、注重基础知识、注重核心概念、倡导回归本源。
目前的实际情况,高三复习课往往所用的资料各类教辅用书代替教材,用做题目代替一切。其实就,高考考题分析,越来越重视教材、重视知识的形成过程、重视高考真的研读。命题专家重视教材作用,发挥教材功能,在命题手法上,常通过教材上例题、习题等题目的改造、移植、嫁接等,编制出立意深远、背景丰富、表述简洁的新题。这就提醒我们要重视教材的作用,强化解题基本功。
分析:教材中推导等比数列前 项和的方法是错位相减法,此种方法虽然是一种典型的处理数列的方法,但学生也很难达到十分熟练的程度,错位相减法的数列求和中的地位又是相当重要的,所以通过公式的推导让学生思维上回归到书本。
(一)回归教材,注重知识形成
以上过程的相反过程就是裂项相消法,这样的教学过程既巩固了裂项相消法,又训练了学生的逆向思维能力。(可用分析法证明)
小结:回归课本将公式进行推导不是一种简单的重复,而是对数学思想、解题方法在学生心中的一种重塑,一种唤醒的方式。这样一方面能使知识得到复习,另一方面也不用通过大量的题目来得到或回顾上面的几种求和的方法,是真正意义上的二轮复习。
(湖南2012,第21题)
(人教A版必修5第76页,第11题)
(二)回归教材,挖掘习题功能
(2015陕西,第21题)
(人教版A必修五第69页习题第4题(3))
分析:(1)先求和再求导最后令x=2得出结论。
也可以先求导再求和最后令x=2得出结论。
(三)考题“重现” 注重类比分析
(17浙江卷,22题)
[06年浙江卷,22题]
再现考题
说明:2017年2题第(3)小题与2006年22题第(2)小题证明的是同一个结论.06年的题直接从导数的儿何意义出发设计问题,而17年的题隐去了导数的儿何意义,需要考生去挖掘,对考生的数学能力来说是挑战。由此可见关注以往的高考考题是有必要的。
(三)考题“重现” 注重类比分析
(17浙江卷,21题)
(08浙江卷,20题)
(三)考题重现,注重类比分析
(三)考题“重现” 注重类比分析
除了以上所列举的,其实2017年的浙江卷第7题由2007年理科卷第8题改编而来;第15题由2014年理科卷第8题改编而来;第17题由2008年理科卷第15题改编而来;
高考试题源于课本与以往的高考题,至少有两个理由:
1. 命题设计尽可能地从现实问题或熟悉背景出发,构造出素材朴实、内蕴丰富的试题,充分体现数学的内在实质试卷中的题目处处闪现着问题解决的智慧。
2.同时也是高考公平性的体现。这样可以很好的引导教师、学生避兔将大量的精力消耗在盲目套所谓技巧上,只要会思考、具有良好思维品质就能考出优异成绩。
(三)考题“重现” 注重类比分析
函数导数与数列型不等式的交汇问题,体现了导数的工具性,凸显了知识之间的纵横联系,一些题构思精巧、新颖,加强对能力的考察,逐渐成为高考的新亮点。2017年浙江22题就是这样的问题。
2017浙江高考22题
四. 考题三研读---重视函数背景下的数列不等式
三现考题
四. 考题三研读---重视函数背景下的数列不等式
评注: 从上面的解答方法可以看出,解决问题的方法为由函数得到函数不等式,进而对x取值,再得到数列不等式,达到解决问题的目的。在此过程中有两个关键步骤:其一是如何得到函数不等式;其二是如何由函数不等式过渡到数列不等式
四. 考题三研读---重视函数背景下的数列不等式
例如:
四. 考题三研读---重视函数背景下的数列不等式
四. 考题三研读---重视函数背景下的数列不等式
四. 考题三研读---重视函数背景下的数列不等式
下面我们一起看看2018年各地市的模拟考试题
四. 考题三研读---重视函数背景下的数列不等式
(2017年9月湖衢丽统测卷22题)
四. 从函数不等式到数列不等式
(2018年1月湖衢丽统测卷22题)
四. 从函数不等式到数列不等式
(2018年1月湖衢丽统测卷22题)
四. 从函数不等式到数列不等式
4.(2018年1月台州统测22题)
四. 从函数不等式到数列不等式
方法小结:
构造函数
函数不等式
数列不等式
放缩和求和
解决问题
二轮复习建议:
了解学情,有的放矢.回归教材,研究考题
谢谢各位专家同仁
同课章节目录
