江西省上饶市横峰中学2012-2013学年高二第一次月考数学(文)试题
文档属性
| 名称 | 江西省上饶市横峰中学2012-2013学年高二第一次月考数学(文)试题 |  | |
| 格式 | zip | ||
| 文件大小 | 145.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2012-09-25 20:57:49 | ||
图片预览


文档简介
横峰中学2012-2013学年高二第一次月考数学(文)试题
一、选择题:本大题共10小题,每小题5分,共50分.在每小题列出的四个选项中,只有一项是符合题目要求的.
1. 若,且,则下列不等式一定成立的是 ( )
A. B. C. D.
2.棱长都是的三棱锥的表面积为( )
A. B. C. D.
3.直线=1在y轴上的截距是( )
A.|| B.± C.- 2 D. 2
4. 如图给出了计算的值的程序框图,
其中①②分别是( )
A. B.
C. D.
由公差为d的等差数列a1、a2、a3…重新组成的
数列a1+a4, a2+a5, a3+a6…是( )
A.公差为d的等差数列 B.公差为2d的等差数列
C.公差为3d的等差数列 D.非等差数列
6.数列{}的通项公式为达到最小值时,=( )
A. 21 B. 22 C. 23 D. 24
7.对在△ABC中,,则最小内角是( )
A.600 B.450 C.300 D.都不是
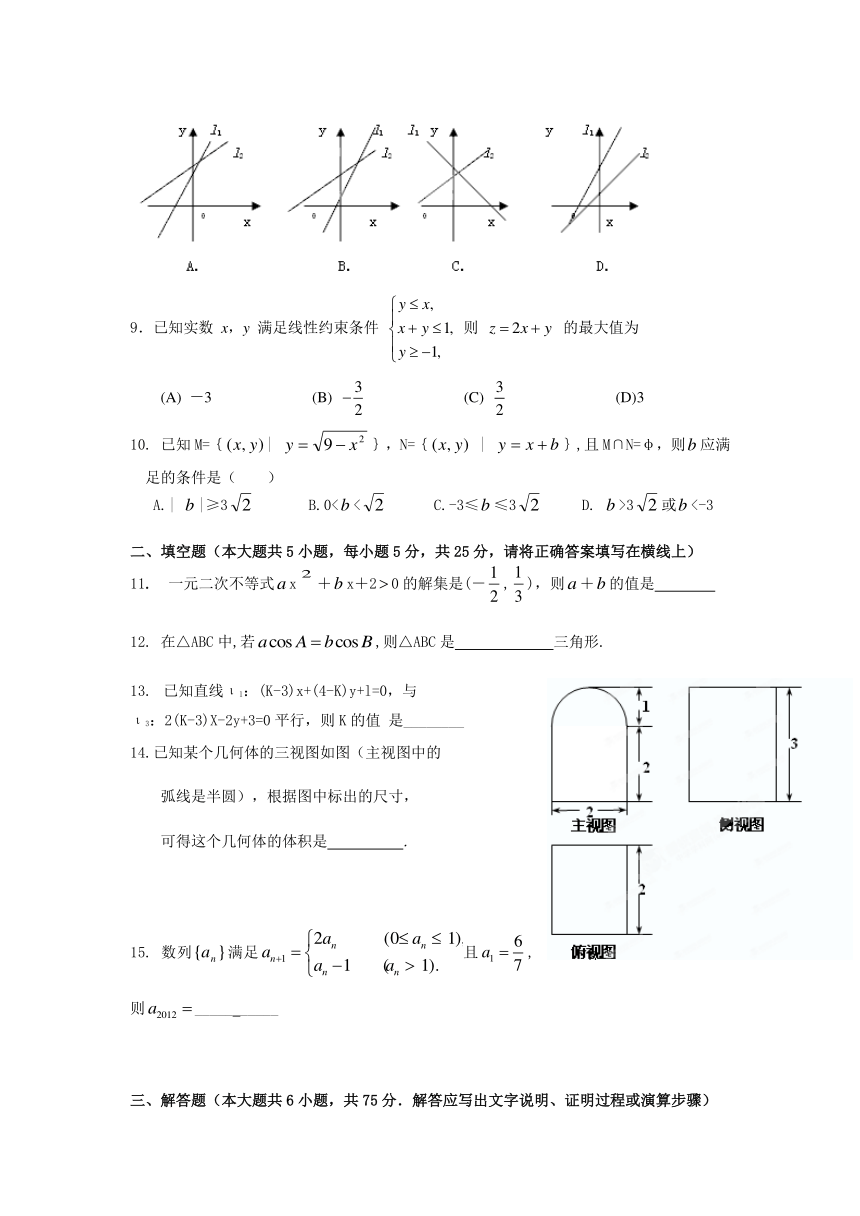
8.l1: +=0, l2: +=0(≠0, ≠0, ≠)的图形可能是( )
9.已知实数 x,y 满足线性约束条件 则 的最大值为
(A) -3 (B) (C) (D)3
10. 已知M={| },N={ | },且M∩N=φ,则应满足的条件是( )
A.| |≥3 B.0<< C.-3≤≤3 D. >3或<-3
二、填空题(本大题共5小题,每小题5分,共25分,请将正确答案填写在横线上)
11. 一元二次不等式x+x+20的解集是(-,),则+的值是
12. 在△ABC中,若,则△ABC是 三角形.
13. 已知直线ι1:(K-3)x+(4-K)y+l=0,与
ι3:2(K-3)X-2y+3=0平行,则K的值 是________
14.已知某个几何体的三视图如图(主视图中的
弧线是半圆),根据图中标出的尺寸,
可得这个几何体的体积是 .
15. 数列满足且,则_____ _____
三、解答题(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤)
16.( 12分)已知集合
(1)若的取值范围;
(2)若的值。
17. ( 12分)过点作一直线,使它与两坐标轴相交且与两轴所围成的三角形面积为,求直线的方程
18.( 12分)设圆的方程为+--=,
(1).求该圆的圆心坐标及半径;
(2).若此圆的一条弦的中点为(3,1),求直线的方程
19.( 12分)如图,ABCD是正方形,O是正方形的中心,PO底面ABCD,E是PC的中点。
求证:(1)PA∥平面BDE; (2)平面PAC平面BDE.
20.( 13分) 在△ABC中,三角A、B、C所对三边a、b、,其中a、b是
方程x2-2x+2=0的两根,且2cos (A+B)=-1.
求角C的度数; (2) 求c; (3) 求△ABC的面积.
21.(14分)已知数列{}的前项和为,且对一切正整数成立.
(1)证明:数列{3+}是等比数列,并求出数列{}的通项公式;
(2)设=, 求数列{}的前 项和为;
(3) 数列{}中是否存在构成等差数列的四项 若存在求出一组;否则说明理由.
高二数学 (文)第一次月考试卷参考答案
时, …………8分
(2)要满足,显然且时成立,
此时
而,故所求的值为3。 …………12分
17.解:设直线为交轴于点,交轴于点,。。。4分
。。。。。6分
得,或 。。。。。。8分
解得或
,或为所求。
18.解(1)将+-4-5=0配方得. ()+=9
圆心坐标为(2.0). 半经为=3. ………6分
(2)设直线的斜率为. 由圆的知识可知: ⊥.
∴
又==1。
直线的方程为()即: ……12分
19.证明(1)∵O是AC的中点,E是PC的中点,∴OE∥AP,
又∵OE平面BDE,PA平面BDE,∴PA∥平面BDE ……6分
(2)∵PO底面ABCD,∴POBD,
又∵ACBD,且ACPO=O
∴BD平面PAC,
而BD平面BDE,∴平面PAC平面BDE。………12分
20.解:(1)∵2cos(A+B)=1,∴cosC=-.∴角C的度数为120°. ………4分
(2)∵a、b是方程x2-2x+2=0的两根,∴a+b=2,ab=2,
c2=a2+b2-2abcosC=(a+b)2-2ab(cosC+1)=12-2=10.∴c=. ………10分
(3)S=absinC=. ………13分
21.解:(1)由n=(3n+Sn)
由待定系数法得 又
∴数列{n+3}是以6为首项,2为公比的等比数列. ∴n+3=6×2n-1, ∴n=3(2n-1). ……4分
(2)∵ bn=n=n2n-n, ∴Bn=2+. ………9分
(3)假设数列{n}存在构成等差数列的四项依次为: 、、、(m则3(2m-1)+3(2q-1)=3(2n-1)+3(2p-1) ∴2m+2q=2n+2p.
上式两边同除以2m,则1+2q-m=2n-m+2p-m
∵m、n、p、q∈N*,且m∴数列{n}不存在构成等差数列的四项. ………14分
开始
S=0,n=2,i=1
S=S+
输出S
①
②
i=i+1
结束
否
是
20080416
一、选择题:本大题共10小题,每小题5分,共50分.在每小题列出的四个选项中,只有一项是符合题目要求的.
1. 若,且,则下列不等式一定成立的是 ( )
A. B. C. D.
2.棱长都是的三棱锥的表面积为( )
A. B. C. D.
3.直线=1在y轴上的截距是( )
A.|| B.± C.- 2 D. 2
4. 如图给出了计算的值的程序框图,
其中①②分别是( )
A. B.
C. D.
由公差为d的等差数列a1、a2、a3…重新组成的
数列a1+a4, a2+a5, a3+a6…是( )
A.公差为d的等差数列 B.公差为2d的等差数列
C.公差为3d的等差数列 D.非等差数列
6.数列{}的通项公式为达到最小值时,=( )
A. 21 B. 22 C. 23 D. 24
7.对在△ABC中,,则最小内角是( )
A.600 B.450 C.300 D.都不是
8.l1: +=0, l2: +=0(≠0, ≠0, ≠)的图形可能是( )
9.已知实数 x,y 满足线性约束条件 则 的最大值为
(A) -3 (B) (C) (D)3
10. 已知M={| },N={ | },且M∩N=φ,则应满足的条件是( )
A.| |≥3 B.0<< C.-3≤≤3 D. >3或<-3
二、填空题(本大题共5小题,每小题5分,共25分,请将正确答案填写在横线上)
11. 一元二次不等式x+x+20的解集是(-,),则+的值是
12. 在△ABC中,若,则△ABC是 三角形.
13. 已知直线ι1:(K-3)x+(4-K)y+l=0,与
ι3:2(K-3)X-2y+3=0平行,则K的值 是________
14.已知某个几何体的三视图如图(主视图中的
弧线是半圆),根据图中标出的尺寸,
可得这个几何体的体积是 .
15. 数列满足且,则_____ _____
三、解答题(本大题共6小题,共75分.解答应写出文字说明、证明过程或演算步骤)
16.( 12分)已知集合
(1)若的取值范围;
(2)若的值。
17. ( 12分)过点作一直线,使它与两坐标轴相交且与两轴所围成的三角形面积为,求直线的方程
18.( 12分)设圆的方程为+--=,
(1).求该圆的圆心坐标及半径;
(2).若此圆的一条弦的中点为(3,1),求直线的方程
19.( 12分)如图,ABCD是正方形,O是正方形的中心,PO底面ABCD,E是PC的中点。
求证:(1)PA∥平面BDE; (2)平面PAC平面BDE.
20.( 13分) 在△ABC中,三角A、B、C所对三边a、b、,其中a、b是
方程x2-2x+2=0的两根,且2cos (A+B)=-1.
求角C的度数; (2) 求c; (3) 求△ABC的面积.
21.(14分)已知数列{}的前项和为,且对一切正整数成立.
(1)证明:数列{3+}是等比数列,并求出数列{}的通项公式;
(2)设=, 求数列{}的前 项和为;
(3) 数列{}中是否存在构成等差数列的四项 若存在求出一组;否则说明理由.
高二数学 (文)第一次月考试卷参考答案
时, …………8分
(2)要满足,显然且时成立,
此时
而,故所求的值为3。 …………12分
17.解:设直线为交轴于点,交轴于点,。。。4分
。。。。。6分
得,或 。。。。。。8分
解得或
,或为所求。
18.解(1)将+-4-5=0配方得. ()+=9
圆心坐标为(2.0). 半经为=3. ………6分
(2)设直线的斜率为. 由圆的知识可知: ⊥.
∴
又==1。
直线的方程为()即: ……12分
19.证明(1)∵O是AC的中点,E是PC的中点,∴OE∥AP,
又∵OE平面BDE,PA平面BDE,∴PA∥平面BDE ……6分
(2)∵PO底面ABCD,∴POBD,
又∵ACBD,且ACPO=O
∴BD平面PAC,
而BD平面BDE,∴平面PAC平面BDE。………12分
20.解:(1)∵2cos(A+B)=1,∴cosC=-.∴角C的度数为120°. ………4分
(2)∵a、b是方程x2-2x+2=0的两根,∴a+b=2,ab=2,
c2=a2+b2-2abcosC=(a+b)2-2ab(cosC+1)=12-2=10.∴c=. ………10分
(3)S=absinC=. ………13分
21.解:(1)由n=(3n+Sn)
由待定系数法得 又
∴数列{n+3}是以6为首项,2为公比的等比数列. ∴n+3=6×2n-1, ∴n=3(2n-1). ……4分
(2)∵ bn=n=n2n-n, ∴Bn=2+. ………9分
(3)假设数列{n}存在构成等差数列的四项依次为: 、、、(m
上式两边同除以2m,则1+2q-m=2n-m+2p-m
∵m、n、p、q∈N*,且m
开始
S=0,n=2,i=1
S=S+
输出S
①
②
i=i+1
结束
否
是
20080416
同课章节目录
