1.5.1乘方
图片预览



文档简介
(共13张PPT)
1次
2次
20次
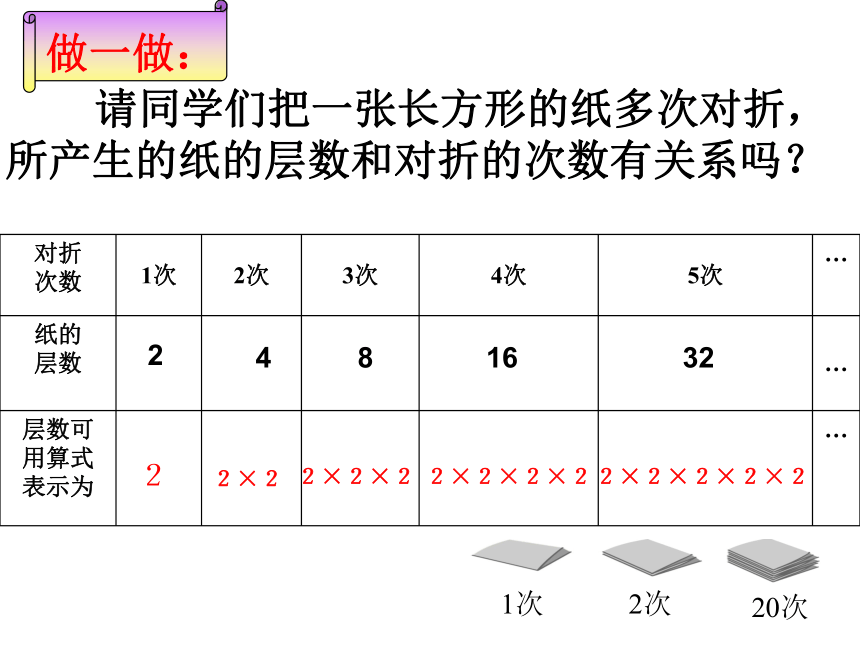
请同学们把一张长方形的纸多次对折,所产生的纸的层数和对折的次数有关系吗?
对折
次数 1次 2次 3次 4次 5次 …
纸的
层数
…
层数可
用算式
表示为 …
2
4
8
16
32
2
2×2×2
2×2×2×2
2×2×2×2×2
2×2
做一做:
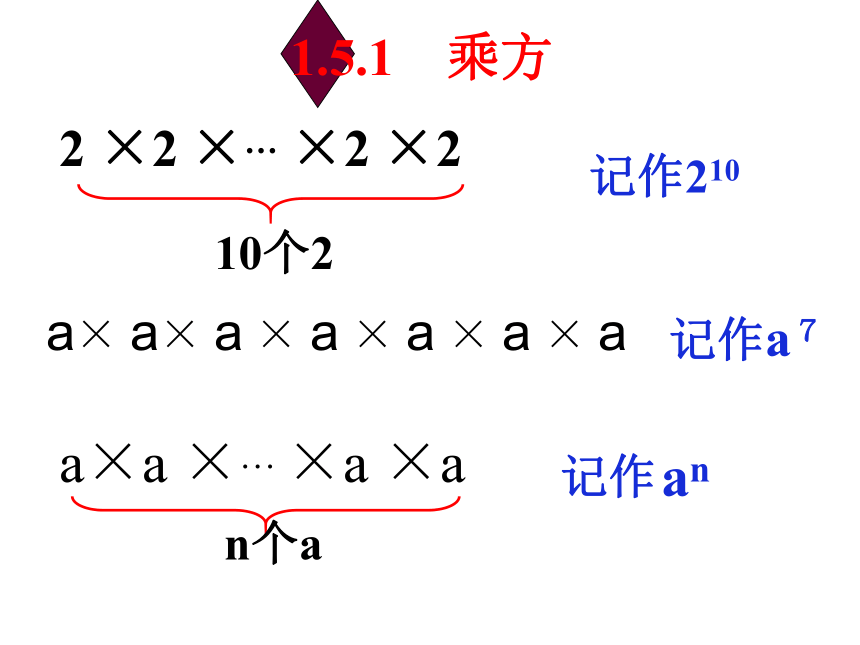
2 ×2 ×… ×2 ×2
10个2
记作210
a×a ×… ×a ×a
n个a
1.5.1 乘方
记作
an
a× a× a × a × a × a × a
记作a7
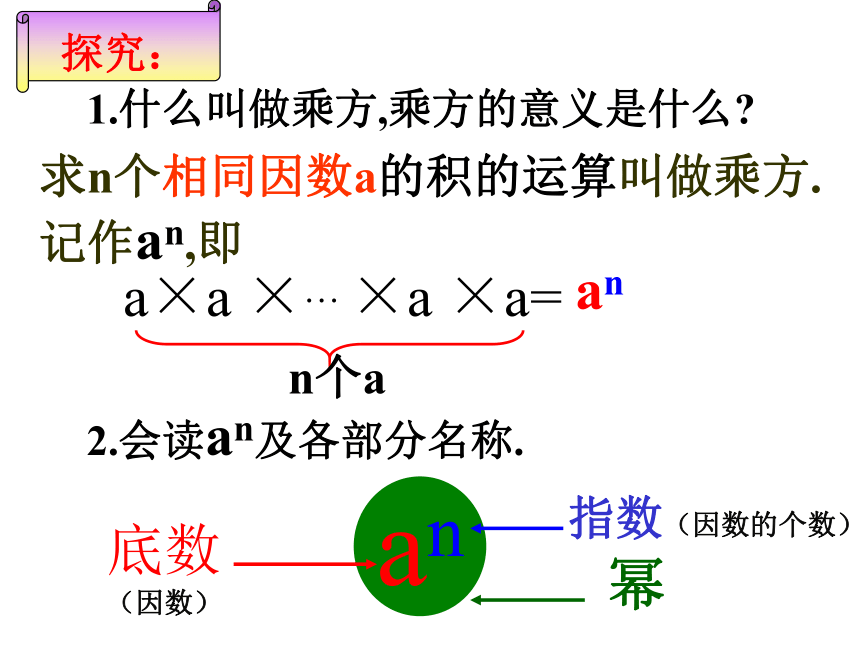
1.什么叫做乘方,乘方的意义是什么
2.会读an及各部分名称.
指数(因数的个数)
幂
底数
(因数)
求n个相同因数a的积的运算叫做乘方.记作an,即
an
a×a ×… ×a ×a=
n个a
an
探究:
1、(口答)
把下列相同因数的乘积
写成幂的形式,并说出底数和指数:
(1) (-6)×(-6) ×(-6)
底数是 –6,指数是 3。
(2)
底数是 ,
指数是 4。
温馨提示:幂的底数是分数或负数时,底数要添上括号!
2、把 写成几个相同因数相乘的形式。
3、把(-2)× (-2)× (-2)×···×(-2)
10个(-2)
写成幂的形式。
议一议:
(-3)2与-32有什么区别?
在(-3)2 中,底数是-3,指数是2,表示2个-3相乘.
在-32 中,底数是3,指数是2,表示2个3相乘的相反数.
例:计算
(1)32 24 16
(2)51 23 19
(3)(-3)2 (-2)6 (-3)4
(4)(-2)5 (-3)3 (-1)3
(5)02 03 04 09
=9
=16
=1
=-32
=-27
=-1
=81
=64
=9
=0
=0
=0
=0
=5
=8
=1
有理数乘方的规律:
1、正数的任何次幂都是正数;
2、负数的偶次幂是正数,负数的奇次幂是负数;
3 、零的任何正整数次幂都是零。
不计算确定下列幂的正负。
(-3)13 (-2)24 (-1.7)2003
(-2)23 02004 (-3.9)12
(负)
(正)
(负)
(负)
(零)
(正)
注意:“一看底数,二看指数”
试一试:
计算:
102 = 103 =
104 = 105 =
10的几次幂,1的后面就有几个0。
100
1000
10000
观察计算的结果,你能发现什么规律?
100000
想一想:
1、填表:
底数 -1 2 10
指数 3 5 4
幂 (-4)3 0.34
(-1)3
25
-4
3
4
0.3
104
2、判断:(对的画“√”,错的画“×”。)
(1) 32 = 3×2 = 6; ( )
(2) (-2)3 = (-3)2; ( )
(3) -32 = (-3)2; ( )
×
×
×
练一练:
课堂小结
1、乘方的概念:求n个相同因数的积的运算叫做乘方。
2、乘方符号的确定:
an
底数
幂(乘方的结果叫做幂)
指数
an读法:a的n次方或a的n次幂
负数的奇次幂是负数,负数的偶次幂是正数,正数的任何次幂都是正数,0的任何正整数次幂都是0。
2、若 ,则x的值是 ___ ;若 ,则a的值是_____ 。
1、(+1)2003 -(- 1)2002=___ 。
0
-2
x2=9
a3=-8
3、某种细胞每过30分钟便由一个分裂 成2个。经过5小时,这种细胞由一个分裂 成了( )个。
210
拓展延伸
1次
2次
20次
请同学们把一张长方形的纸多次对折,所产生的纸的层数和对折的次数有关系吗?
对折
次数 1次 2次 3次 4次 5次 …
纸的
层数
…
层数可
用算式
表示为 …
2
4
8
16
32
2
2×2×2
2×2×2×2
2×2×2×2×2
2×2
做一做:
2 ×2 ×… ×2 ×2
10个2
记作210
a×a ×… ×a ×a
n个a
1.5.1 乘方
记作
an
a× a× a × a × a × a × a
记作a7
1.什么叫做乘方,乘方的意义是什么
2.会读an及各部分名称.
指数(因数的个数)
幂
底数
(因数)
求n个相同因数a的积的运算叫做乘方.记作an,即
an
a×a ×… ×a ×a=
n个a
an
探究:
1、(口答)
把下列相同因数的乘积
写成幂的形式,并说出底数和指数:
(1) (-6)×(-6) ×(-6)
底数是 –6,指数是 3。
(2)
底数是 ,
指数是 4。
温馨提示:幂的底数是分数或负数时,底数要添上括号!
2、把 写成几个相同因数相乘的形式。
3、把(-2)× (-2)× (-2)×···×(-2)
10个(-2)
写成幂的形式。
议一议:
(-3)2与-32有什么区别?
在(-3)2 中,底数是-3,指数是2,表示2个-3相乘.
在-32 中,底数是3,指数是2,表示2个3相乘的相反数.
例:计算
(1)32 24 16
(2)51 23 19
(3)(-3)2 (-2)6 (-3)4
(4)(-2)5 (-3)3 (-1)3
(5)02 03 04 09
=9
=16
=1
=-32
=-27
=-1
=81
=64
=9
=0
=0
=0
=0
=5
=8
=1
有理数乘方的规律:
1、正数的任何次幂都是正数;
2、负数的偶次幂是正数,负数的奇次幂是负数;
3 、零的任何正整数次幂都是零。
不计算确定下列幂的正负。
(-3)13 (-2)24 (-1.7)2003
(-2)23 02004 (-3.9)12
(负)
(正)
(负)
(负)
(零)
(正)
注意:“一看底数,二看指数”
试一试:
计算:
102 = 103 =
104 = 105 =
10的几次幂,1的后面就有几个0。
100
1000
10000
观察计算的结果,你能发现什么规律?
100000
想一想:
1、填表:
底数 -1 2 10
指数 3 5 4
幂 (-4)3 0.34
(-1)3
25
-4
3
4
0.3
104
2、判断:(对的画“√”,错的画“×”。)
(1) 32 = 3×2 = 6; ( )
(2) (-2)3 = (-3)2; ( )
(3) -32 = (-3)2; ( )
×
×
×
练一练:
课堂小结
1、乘方的概念:求n个相同因数的积的运算叫做乘方。
2、乘方符号的确定:
an
底数
幂(乘方的结果叫做幂)
指数
an读法:a的n次方或a的n次幂
负数的奇次幂是负数,负数的偶次幂是正数,正数的任何次幂都是正数,0的任何正整数次幂都是0。
2、若 ,则x的值是 ___ ;若 ,则a的值是_____ 。
1、(+1)2003 -(- 1)2002=___ 。
0
-2
x2=9
a3=-8
3、某种细胞每过30分钟便由一个分裂 成2个。经过5小时,这种细胞由一个分裂 成了( )个。
210
拓展延伸
