2021-2022学年安徽省宣城六中九年级(上)期中数学试卷(Word版含解析)
文档属性
| 名称 | 2021-2022学年安徽省宣城六中九年级(上)期中数学试卷(Word版含解析) |  | |
| 格式 | doc | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 08:55:54 | ||
图片预览



文档简介
2021-2022学年安徽省宣城六中九年级第一学期期中数学试卷
一、选择题(本大题共10小题,每小题4分,满分40分)(每小题都给出了A,B,C,D四个选项,其中只有一个是正确的)
1.若函数y=(a﹣1)x2+2x+a2﹣1是关于x的二次函数,则( )
A.a≠1 B.a≠﹣1 C.a=1 D.a=±1
2.关于二次函数y=2x2﹣8x,下列结论中正确的是( )
A.图象与x轴有两个交点
B.当x=2时,y有最大值﹣8
C.当x>1时,y随x的增大而增大
D.函数图象开口向下
3.若二次函数y=kx2﹣4x﹣2与x轴有两个不同的交点,则k的取值范围是( )
A.k>﹣2 B.k>﹣2且k≠0 C.k<2 D.k≥﹣2且k≠0
4.对于反比例函数,下列结论:①图象分布在第二、四象限;②当x>0时,y随x的增大而增大;③图象经过点(1,﹣2);④若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则y1<y2,其中正确的是( )
A.①②③ B.②③④ C.①③④ D.①②④
5.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),则下列结论中正确的是( )
A.AB2=AP2+BP2 B.BP2=AP BA
C. D.
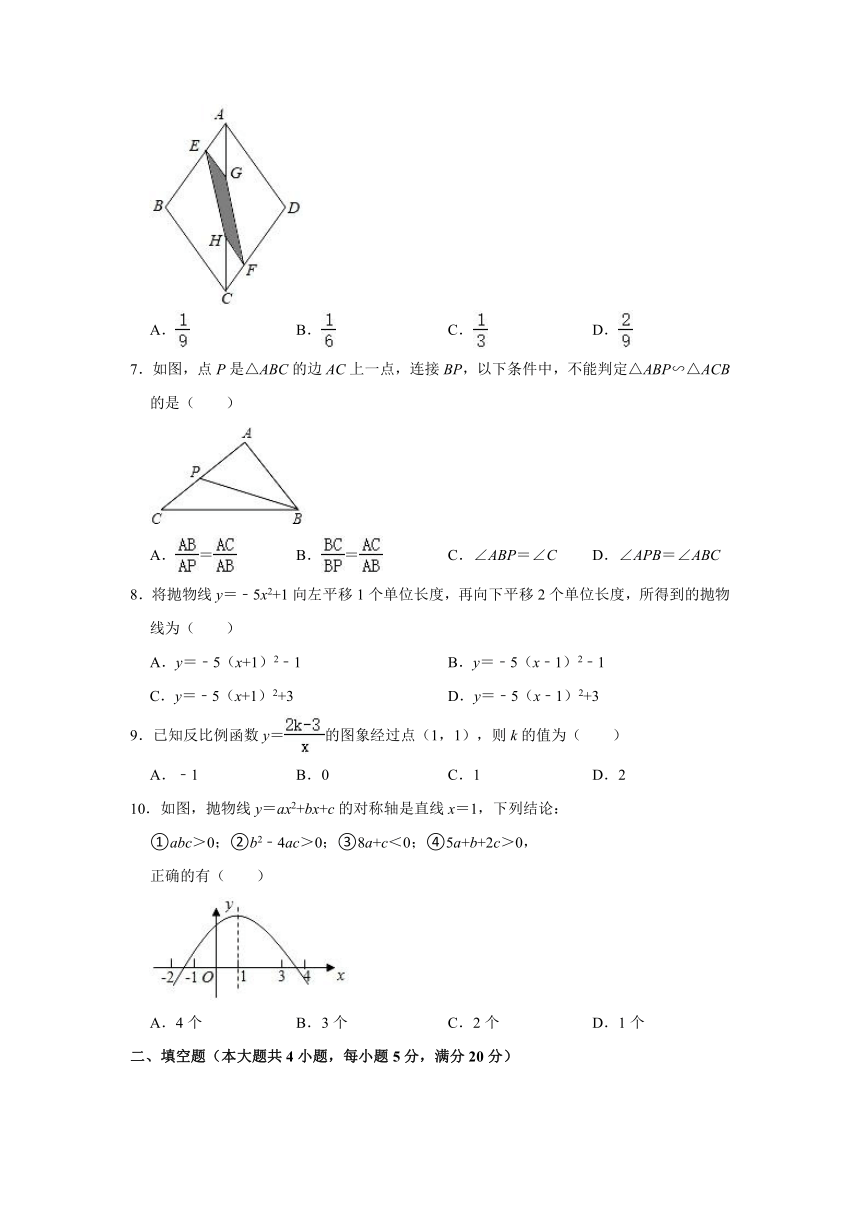
6.如图,在菱形ABCD中,点E,F分别在AB,CD上,且BE=2AE,DF=2CF,点G,H分别是AC的三等分点,则的值为( )
A. B. C. D.
7.如图,点P是△ABC的边AC上一点,连接BP,以下条件中,不能判定△ABP∽△ACB的是( )
A.= B.= C.∠ABP=∠C D.∠APB=∠ABC
8.将抛物线y=﹣5x2+1向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为( )
A.y=﹣5(x+1)2﹣1 B.y=﹣5(x﹣1)2﹣1
C.y=﹣5(x+1)2+3 D.y=﹣5(x﹣1)2+3
9.已知反比例函数y=的图象经过点(1,1),则k的值为( )
A.﹣1 B.0 C.1 D.2
10.如图,抛物线y=ax2+bx+c的对称轴是直线x=1,下列结论:
①abc>0;②b2﹣4ac>0;③8a+c<0;④5a+b+2c>0,
正确的有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知,则的值为 .
12.如图,直线y=x+m与双曲线y=相交于A,B两点,BC∥x轴,AC∥y轴,则△ABC面积的最小值为 .
13.如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长 .
14.如图,正方形ABCD中,点E是BC的中点,点F是CD上一点,分别以AE、AF为对称轴,折叠△ABE、△ADF,使得AB和AD与AG重合,连接BG交AE于点H,连接CG.
(1)HE:AH= ;
(2)S△AFE:S正方形ABCD= .
三、(本大题共2小题,每小题8分,满分16分)
15.若二次函数的图象的对称轴方程是x=,并且图象过A(0,﹣4)和B(4,0)
(1)求此二次函数图象上点A关于对称轴x=对称的点A′的坐标;
(2)求此二次函数的解析式.
16.如图,矩形OABC的两个顶点A,C分别在y轴和x轴上,边AB和BC与反比例函数y1=(x>0)和y2=(k>0,x>0)图象交于E,F和点H,G.AE:AF=2:3.
(1)求反比例函数y2的解析式;
(2)若点C的坐标为(8,0),求GH的长.
四、(本大题共2小题,每小题8分,满分16分)
17.已知抛物线y=(x﹣m)2﹣(x﹣m),其中m是常数.
(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x=.
①求该抛物线的函数解析式;
②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点.
18.已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.求证:△ABD∽△DCE.
五、(本大题共2小题,每小题10分,满分20分)
19.已知:△ABC中,∠C=90°,正方形DEFG,点D、G分别在AC、BC上,E、F在AB上;
(1)若AC=3,BC=4,求DG的长;
(2)如图2,四边形HPEQ、MNRF为正方形,设正方形HPEQ、MFRN、DEFG的边长分别为a、b、c,求证:a+b=c.
20.某商店经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天) 1≤x<50 50≤x≤90
售价(元/件) x+40 90
每天销量(件) 200﹣2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
六、(本题满分12分)
21.抛物线y=mx2﹣4m(m>0)与x轴交于A,B两点(A点在B点左边),与y轴交于C点,已知OC=2OA.求:
(1)A,B两点的坐标;
(2)抛物线的解析式.
七、(本题满分12分)
22.如图1,在△ABC中,AC=BC,点D,E,F分别是线段AC,BC,AD的中点,BF,ED的延长线交于点G.
(1)求证:AB=GD;
(2)如图2,连接GC,当CG=EG时,求的值.
八、(本题满分14分)
23.如图,在Rt△ABC中,CA=CB,M是AB的中点,点D在BM上,AE⊥CD,BF⊥
CD,垂足分别为E,F,连接EM.
①试证明:BF=CE;
②图中线段AE、CE与ME三者之间有何关系?并说明理由;
③求证:CF DM=BM DE.
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)(每小题都给出了A,B,C,D四个选项,其中只有一个是正确的)
1.若函数y=(a﹣1)x2+2x+a2﹣1是关于x的二次函数,则( )
A.a≠1 B.a≠﹣1 C.a=1 D.a=±1
【分析】利用二次函数定义进行解答即可.
解:由题意得:a﹣1≠0,
解得:a≠1,
故选:A.
2.关于二次函数y=2x2﹣8x,下列结论中正确的是( )
A.图象与x轴有两个交点
B.当x=2时,y有最大值﹣8
C.当x>1时,y随x的增大而增大
D.函数图象开口向下
【分析】根据函数解析式和二次函数的性质逐个判断即可.
解:∵二次函数y=2x2﹣8x=2(x﹣2)2﹣8,
∴抛物线的开口向上,对称轴为直线x=2,顶点为(2,﹣8),当x=2时,y有最小值﹣8,
∴当x>2时,y随x的增大而增大,
故B、C、D结论不正确,
∵y=2x2﹣8x=2x(x﹣4),
∴二次函数y=2x2﹣8x与x轴的交点为(0,0),(4,0),
故A正确;
故选:A.
3.若二次函数y=kx2﹣4x﹣2与x轴有两个不同的交点,则k的取值范围是( )
A.k>﹣2 B.k>﹣2且k≠0 C.k<2 D.k≥﹣2且k≠0
【分析】由抛物线与x轴有两个不同的交点可得出一元二次方程kx2﹣4x﹣2=0有两个不相等的解,由二次项系数非零及根的判别式Δ>0,即可得出关于k的一元一次不等式组,解之即可得出结论.
解:令y=0,则kx2﹣4x﹣2=0,
∵二次函数y=kx2﹣4x﹣2的图象与x轴有两个不同的交点,
∴一元二次方程kx2﹣4x﹣2=0有两个不相等的解,
∴,
解得:k>﹣2且k≠0.
故选:B.
4.对于反比例函数,下列结论:①图象分布在第二、四象限;②当x>0时,y随x的增大而增大;③图象经过点(1,﹣2);④若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则y1<y2,其中正确的是( )
A.①②③ B.②③④ C.①③④ D.①②④
【分析】根据题目中的函数解析式和反比例函数的性质,可以判断各个小题中的结论是否正确.
解:∵于反比例函数,
∴该函数的图象分布在第二、四象限,故①正确;
当x>0时,y随x的增大而增大,故②正确;
当x=1时,y=﹣2,故③正确;
若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则点A和点B都在第二象限或都在第四象限时y1<y2,点A在第二象限,点B在第四象限时y1>y2,故④错误;
故选:A.
5.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),则下列结论中正确的是( )
A.AB2=AP2+BP2 B.BP2=AP BA
C. D.
【分析】由黄金分割的定义得AP2=BP BA,==,即可求解.
解:∵P为AB的黄金分割点(AP>PB),
∴AP2=BP BA,==,故选项A、B、C不符合题意,选项D符合题意,
故选:D.
6.如图,在菱形ABCD中,点E,F分别在AB,CD上,且BE=2AE,DF=2CF,点G,H分别是AC的三等分点,则的值为( )
A. B. C. D.
【分析】由题意可证EG∥BC,HF∥AD,根据比例式即可求解.
解:∵BE=2AE,DF=2FC,
∴,
∵G、H分别是AC的三等分点,
∴,,
∴,
∴EG∥BC
∴,
同理可得HF∥AD,,
∴,
故选:A.
7.如图,点P是△ABC的边AC上一点,连接BP,以下条件中,不能判定△ABP∽△ACB的是( )
A.= B.= C.∠ABP=∠C D.∠APB=∠ABC
【分析】根据相似三角形的判定定理(①有两角分别相等的两三角形相似,②有两边的比相等,并且它们的夹角也相等的两三角形相似)逐个进行判断即可.
解:A、∵∠A=∠A,=,
∴△ABP∽△ACB,故本选项错误;
B、根据=和∠A=∠A不能判断△ABP∽△ACB,故本选项正确;
C、∵∠A=∠A,∠ABP=∠C,
∴△ABP∽△ACB,故本选项错误;
D、∵∠A=∠A,∠APB=∠ABC,
∴△ABP∽△ACB,故本选项错误;
故选:B.
8.将抛物线y=﹣5x2+1向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为( )
A.y=﹣5(x+1)2﹣1 B.y=﹣5(x﹣1)2﹣1
C.y=﹣5(x+1)2+3 D.y=﹣5(x﹣1)2+3
【分析】直接利用二次函数图象与几何变换的性质分别平移得出答案.
解:将抛物线y=﹣5x2+1向左平移1个单位长度,得到y=﹣5(x+1)2+1,再向下平移2个单位长度,
所得到的抛物线为:y=﹣5(x+1)2﹣1.
故选:A.
9.已知反比例函数y=的图象经过点(1,1),则k的值为( )
A.﹣1 B.0 C.1 D.2
【分析】把点的坐标代入函数解析式得出方程,求出方程的解即可.
解:∵反比例函数y=的图象经过点(1,1),
∴代入得:2k﹣3=1×1,
解得:k=2,
故选:D.
10.如图,抛物线y=ax2+bx+c的对称轴是直线x=1,下列结论:
①abc>0;②b2﹣4ac>0;③8a+c<0;④5a+b+2c>0,
正确的有( )
A.4个 B.3个 C.2个 D.1个
【分析】根据抛物线的开口方向、对称轴、与坐标轴的交点判定系数符号及运用一些特殊点解答问题.
解:由抛物线的开口向下可得:a<0,
根据抛物线的对称轴在y轴右边可得:a,b异号,所以b>0,
根据抛物线与y轴的交点在正半轴可得:c>0,
∴abc<0,故①错误;
∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,故②正确;
∵直线x=1是抛物线y=ax2+bx+c(a≠0)的对称轴,所以﹣=1,可得b=﹣2a,
由图象可知,当x=﹣2时,y<0,即4a﹣2b+c<0,
∴4a﹣2×(﹣2a)+c<0,
即8a+c<0,故③正确;
由图象可知,当x=2时,y=4a+2b+c>0;当x=﹣1时,y=a﹣b+c>0,
两式相加得,5a+b+2c>0,故④正确;
∴结论正确的是②③④3个,
故选:B.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知,则的值为 1 .
【分析】设=k,根据比例的性质得出a=2k,b=3k,c=5k,再代入求出答案即可.
解:设=k,
则a=2k,b=3k,c=5k,
所以==1,
故答案为:1.
12.如图,直线y=x+m与双曲线y=相交于A,B两点,BC∥x轴,AC∥y轴,则△ABC面积的最小值为 6 .
【分析】方法一:根据双曲线y=过A,B两点,可设A(a,),B(b,),则C(a,).将y=x+m代入y=,整理得x2+mx﹣3=0,由于直线y=x+m与双曲线y=相交于A,B两点,所以a、b是方程x2+mx﹣3=0的两个根,根据根与系数的关系得出a+b=﹣m,ab=﹣3,那么(a﹣b)2=(a+b)2﹣4ab=m2+12.再根据三角形的面积公式得出S△ABC=AC BC=m2+6,利用二次函数的性质即可求出当m=0时,△ABC的面积有最小值6.
方法二:先根据△ABC为等腰直角三角形,得出S△ABC=AC BC=AB2,AB最小时,面积最小,即m=0时面积最小,联立方程,得出A,B的坐标,即可求得AB的长,进而得出三角形面积的最小值.
解:方法一:
设A(a,),B(b,),则C(a,).
将y=x+m代入y=,得x+m=,
整理,得x2+mx﹣3=0,
则a+b=﹣m,ab=﹣3,
∴(a﹣b)2=(a+b)2﹣4ab=m2+12.
∵S△ABC=AC BC
=(﹣)(a﹣b)
= (a﹣b)
=(a﹣b)2
=(m2+12)
=m2+6,
∴当m=0时,△ABC的面积有最小值6.
故答案为6.
方法二:
因为y=x+m斜率为1,且BC∥x轴,AC∥y轴
∴∠ABC=∠BAC=45°
∴△ABC为等腰直角三角形
∴AC=BC=AB
∴S△ABC=AC BC=AB2
当AB最小时,m=0,直线为y=x
联立方程,解得或
∴A(,),B(﹣,﹣)
AB=×2=2
∴S△ABC最小=×4×6=6
故答案为6.
13.如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长 .
【分析】证出∠ACD=∠DCB=∠B,证明△ACD∽△ABC,得出=,即可得出结果.
解:∵BC的垂直平分线MN交AB于点D,
∴CD=BD=3,
∴∠B=∠DCB,AB=AD+BD=5,
∵CD平分∠ACB,
∴∠ACD=∠DCB=∠B,
∵∠A=∠A,
∴△ACD∽△ABC,
∴=,
∴AC2=AD×AB=2×5=10,
∴AC=.
故答案为:.
14.如图,正方形ABCD中,点E是BC的中点,点F是CD上一点,分别以AE、AF为对称轴,折叠△ABE、△ADF,使得AB和AD与AG重合,连接BG交AE于点H,连接CG.
(1)HE:AH= 1:4 ;
(2)S△AFE:S正方形ABCD= 5:12 .
【分析】(1)根据翻折的性质得到∠GHE=∠BHE=90°,再根据∠HEB=∠BEA,从而证明△HEB∽△BEA,得出,设正方形边长为2x,则BE=x,AB=2x,由勾股定理求出AE,从而求出HE和AH,得出结论;
(2)由S△AFE=(S正方形ABCD﹣S△FCE),正方形ABCD的边长为2,FG=DF=x,则EF=1+x,CF=2﹣x,由勾股定理求出x即可.
解:(1)∵AE为对称轴,
∴△AEG≌△AEB,BG⊥AE,
∴∠GHE=∠BHE=90°,
又∵∠HEB=∠BEA,
∴△HEB∽△BEA,
∴=,
在正方形ABCD中,设边长为2x,
则BE=x,AB=2x,
∴AE===x,
∴HE===x,
∴AH=AE﹣HE=x﹣x=x,
∴HE:AH=x:x=1:4.
故答案为:1:4;
(2)设正方形ABCD的边长为2,则S正方形ABCD=4,
∵S△AFE=(S正方形ABCD﹣S△FCE),CE=BE=GE=1,
设FG=DF=x,
则EF=1+x,CF=2﹣x,
在△EFC中,
∵EF2=CE2+CF2,
∴(1+x)2=(2﹣x)2+1,
解得:x=,
∴CE=2﹣x=,
∴S△CFE=×CE×CF=××1=,
∴S△AFE=×(4﹣)=,
∴S△AFE:S正方形ABCD=:4=5:12.
故答案为:5:12.
三、(本大题共2小题,每小题8分,满分16分)
15.若二次函数的图象的对称轴方程是x=,并且图象过A(0,﹣4)和B(4,0)
(1)求此二次函数图象上点A关于对称轴x=对称的点A′的坐标;
(2)求此二次函数的解析式.
【分析】(1)直接利用对称性求解即可;
(2)利用待定系数法把A(0,﹣4)和B(4,0),即对称轴x=代入解析式,解三元一次方程组可得y=x2﹣3x﹣4.
解:(1)A′(3,﹣4);
(2)设此二次函数的解析式为y=ax2+bx+c,
由题意,得,
解得.
∴y=x2﹣3x﹣4.
16.如图,矩形OABC的两个顶点A,C分别在y轴和x轴上,边AB和BC与反比例函数y1=(x>0)和y2=(k>0,x>0)图象交于E,F和点H,G.AE:AF=2:3.
(1)求反比例函数y2的解析式;
(2)若点C的坐标为(8,0),求GH的长.
【分析】(1)设E(a,b),根据已知条件求得F(a,b),分别代入解析式得出ab=4,a b=k,从而求得k=6,D得出反比例函数y2的解析式;
(2)把x=8分别代入y1=和y2=,即可求得CG、CH的值,然后根据GH=CG﹣CH即可求得.
解:(1)设E(a,b),
∴AE=a,
∵AE:AF=2:3.
∴AF=a,
∴F(a,b),
∵E是反比例函数y1=(x>0)上的点,
∴ab=4,
∵F是反比例函数(k>0,x>0)图象上的点,
∴a b=k,
∴k=×4=6,
∴反比例函数y2的解析式为y2=.
(2)把x=8分别代入y1=和y2=得,y1=和y2=,
∴CH=,CG=,
∴GH=CG﹣CH=.
四、(本大题共2小题,每小题8分,满分16分)
17.已知抛物线y=(x﹣m)2﹣(x﹣m),其中m是常数.
(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x=.
①求该抛物线的函数解析式;
②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点.
【分析】(1)先把抛物线解析式化为一般式,再计算△的值,得到△=1>0,于是根据Δ=b2﹣4ac决定抛物线与x轴的交点个数即可判断不论m为何值,该抛物线与x轴一定有两个公共点;
(2)①根据对称轴方程得到=﹣=,然后解出m的值即可得到抛物线解析式;
②根据抛物线的平移规律,设抛物线沿y轴向上平移k个单位长度后,得到的抛物线与x轴只有一个公共点,则平移后抛物线解析式为y=x2﹣5x+6+k,再利用抛物线与x轴的只有一个交点得到△=52﹣4(6+k)=0,
然后解关于k的方程即可.
【解答】(1)证明:y=(x﹣m)2﹣(x﹣m)=x2﹣(2m+1)x+m2+m,
∵△=(2m+1)2﹣4(m2+m)=1>0,
∴不论m为何值,该抛物线与x轴一定有两个公共点;
(2)解:①∵x=﹣=,
∴m=2,
∴抛物线解析式为y=x2﹣5x+6;
②设抛物线沿y轴向上平移k个单位长度后,得到的抛物线与x轴只有一个公共点,则平移后抛物线解析式为y=x2﹣5x+6+k,
∵抛物线y=x2﹣5x+6+k与x轴只有一个公共点,
∴△=52﹣4(6+k)=0,
∴k=,
即把该抛物线沿y轴向上平移个单位长度后,得到的抛物线与x轴只有一个公共点.
18.已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.求证:△ABD∽△DCE.
【分析】先判断△ABC为等腰直角三角形得到∠B=∠C=45°,再利用三角形内角和得到∠1+∠2=135°,利用平角定义得到∠2++∠3=135°,则∠1=∠3,于是可根据有两组角对应相等的两个三角形相似得到结论.
【解答】证明:∵∠BAC=90°,AB=AC=1,
∴△ABC为等腰直角三角形,
∴∠B=∠C=45°,
∴∠1+∠2=180°﹣∠B=135°,
∵∠ADE=45°,
∴∠2+∠3=135°,
∴∠1=∠3,
∵∠B=∠C,
∴△ABD∽△DCE.
五、(本大题共2小题,每小题10分,满分20分)
19.已知:△ABC中,∠C=90°,正方形DEFG,点D、G分别在AC、BC上,E、F在AB上;
(1)若AC=3,BC=4,求DG的长;
(2)如图2,四边形HPEQ、MNRF为正方形,设正方形HPEQ、MFRN、DEFG的边长分别为a、b、c,求证:a+b=c.
【分析】(1)过C作CM⊥BA于M,交DG于N,由勾股定理求出AB的长,再由三角形面积计算公式即可求出CM的长,由DG=GF=EF=DE=MN,DG∥BA,得△CDG∽△CAB,再根据相似三角形的性质列出比例式即可求解;
(2)利用两个角相等,可证明△NMG∽△DQH,得,代入即可得出a,b,c的关系.
【解答】(1)解:过C作CM⊥BA于M,交DG于N,
∵△ABC是直角三角形,∠ACB=90°,CB=4,AC=3,
∴BA==5,
由三角形面积公式得:AC×BC=AB×CM,
∵CB=4,AC=3,BA=5,
∴CM=2.4,
∵四边形DEFG是正方形,
∴DG=GF=EF=DE=MN,DG∥BA,
∴△CDG∽△CAB,
∴=,
∴,
∴DG=;
(2)证明:∵∠MGN+∠CGD=90°,∠CDG+∠CGD=90°,
∴∠MGN=∠CDG,
同理,∠DHQ=∠CDG,
∴∠MGN=∠DHQ,
∵∠NMG=∠DQH,
∴△NMG∽△DQH,
∴,即,
∴ab=c2﹣ac﹣bc+ab,
∴0=c2﹣ac﹣bc,
即c2=ac+bc,
∵c>0,
∴a+b=c.
20.某商店经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天) 1≤x<50 50≤x≤90
售价(元/件) x+40 90
每天销量(件) 200﹣2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
【分析】(1)分成1≤x<50和50≤x≤90两种情况进行讨论,利用:利润=每件的利润×销售的件数,即可求得函数的解析式;
(2)结合(1)得到的两个解析式,结合二次函数与一次函数的性质分别求得最值,然后两种情况下取最大的即可.
解:(1)当1≤x<50时,y=(200﹣2x)(x+40﹣30)=﹣2x2+180x+2000,
当50≤x≤90时,
y=(200﹣2x)(90﹣30)=﹣120x+12000,
综上所述:y=;
(2)当1≤x<50时,二次函数开口下,二次函数对称轴为直线x=45,
当x=45时,y最大=﹣2×452+180×45+2000=6050,
当50≤x≤90时,y随x的增大而减小,
当x=50时,y最大=6000,
综上所述,该商品第45天时,当天销售利润最大,最大利润是6050元;
六、(本题满分12分)
21.抛物线y=mx2﹣4m(m>0)与x轴交于A,B两点(A点在B点左边),与y轴交于C点,已知OC=2OA.求:
(1)A,B两点的坐标;
(2)抛物线的解析式.
【分析】(1)通过解方程mx2﹣4m=0可得A、B点的坐标;
(2)先利用OA=2得到OC=4,所以|﹣4m|=4,然后求出满足条件的m的值,从而得到抛物线解析式.
解:(1)当y=0时,mx2﹣4m=0,即x2﹣4=0,解得x1=2,x2=﹣2,
∴A(﹣2,0),B(2,0);
(2)当x=0时,y=mx2﹣4m=﹣4m,
∴C(0,﹣4m),
∵OA=2,
∴OC=2OA=4,
∴|﹣4m|=4,解得m=1或m=﹣1,
∵m>0,
∴m=1,
∴抛物线解析式为y=x2﹣4.
七、(本题满分12分)
22.如图1,在△ABC中,AC=BC,点D,E,F分别是线段AC,BC,AD的中点,BF,ED的延长线交于点G.
(1)求证:AB=GD;
(2)如图2,连接GC,当CG=EG时,求的值.
【分析】(1)由题意可知DE是△ABC的中位线,从而可知EG∥AB,又点F为线段AD的中点,所以AF=DF,然后证明△ABF≌△DGF(ASA),由全等三角形的性质即可得出AB=GD.
(2)由条件可知DE=AB,EG=AB,然后利用DE∥AB,证明△GEC∽△CBA,从而求出的值.
【解答】(1)证明:∵点D,E,F分别是线段AC,BC,AD的中点,
∴DE为△ABC的中位线,AF=DF,
∴ED∥AB,
∴∠A=∠GDF,
在△ABF和△DGF中,
∴△ABF≌△DGF(ASA),
∴AB=GD;
(2)解:∵D、E为AC、BC中点,
∴AC=2DC,BC=2CE,
∵AC=BC,
∴AC=2CE,∠A=∠ABC,
∵EG∥AB,
∴∠GEC=∠ABC=∠EDC=∠A,
∵GE=GC,
∴∠GCE=∠GEC=∠EDC=∠A,
∴△CDE∽△GCE,
∴,
∴EC2=ED GE,
∵DE为△ABC的中位线,
∴DE=AB,
∴GE=DE+GD=AB,
∴CE===AB,
∵AC=2CE,
∴AC=2CE=2×AB,
∴.
八、(本题满分14分)
23.如图,在Rt△ABC中,CA=CB,M是AB的中点,点D在BM上,AE⊥CD,BF⊥
CD,垂足分别为E,F,连接EM.
①试证明:BF=CE;
②图中线段AE、CE与ME三者之间有何关系?并说明理由;
③求证:CF DM=BM DE.
【分析】①证明△BCF≌△CAE,根据等腰三角形的性质即可得到BF=CE;
②连接FM,CM,证明△BFM≌△CEM,从而判断△EMF为等腰直角三角形,得到EF=EM,即可得出AE﹣CE=ME;
③证明△CDM∽ADE,得到对应边成比例,结合BM=CM,AE=CF即可得出结论.
【解答】①证明:∵△ABC是直角三角形,
∠ACB=90°,
∴∠BCF+∠ACE=90°,
∵∠BCF+∠CBF=90°,
∴∠ACE=∠CBF,
又∵∠BFD=90°=∠AEC,AC=BC,
∴△BCF≌△CAE(AAS),
∴BF=CE;
②解:AE﹣CE=ME,
理由:由①得:△BCF≌△CAE,
∴AE=CF,BF=CE,
∴AE﹣CE=CF﹣CE=EF,
连接FM,CM,
∵点M是AB中点,
∴CM=AB=BM=AM,CM⊥AB,
在△BDF和△CDM中,∠BFD=∠CMD,∠BDF=∠CDM,
∴∠DBF=∠DCM,
又BM=CM,BF=CE,
∴△BFM≌△CEM(SAS),
∴FM=EM,∠BMF=∠CME,
∵∠BMC=90°,
∴∠EMF=90°,即△EMF为等腰直角三角形,
∴EF=EM,
∵AE﹣CE=EF,
∴AE﹣CE=EM;
③证明:连接CM,
∵∠CDM=∠ADE,∠CMD=∠AED=90°,
∴△CDM∽△ADE,
∴,
∵BM=CM,AE=CF,
∴,
∴CF DM=BM DE.
一、选择题(本大题共10小题,每小题4分,满分40分)(每小题都给出了A,B,C,D四个选项,其中只有一个是正确的)
1.若函数y=(a﹣1)x2+2x+a2﹣1是关于x的二次函数,则( )
A.a≠1 B.a≠﹣1 C.a=1 D.a=±1
2.关于二次函数y=2x2﹣8x,下列结论中正确的是( )
A.图象与x轴有两个交点
B.当x=2时,y有最大值﹣8
C.当x>1时,y随x的增大而增大
D.函数图象开口向下
3.若二次函数y=kx2﹣4x﹣2与x轴有两个不同的交点,则k的取值范围是( )
A.k>﹣2 B.k>﹣2且k≠0 C.k<2 D.k≥﹣2且k≠0
4.对于反比例函数,下列结论:①图象分布在第二、四象限;②当x>0时,y随x的增大而增大;③图象经过点(1,﹣2);④若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则y1<y2,其中正确的是( )
A.①②③ B.②③④ C.①③④ D.①②④
5.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),则下列结论中正确的是( )
A.AB2=AP2+BP2 B.BP2=AP BA
C. D.
6.如图,在菱形ABCD中,点E,F分别在AB,CD上,且BE=2AE,DF=2CF,点G,H分别是AC的三等分点,则的值为( )
A. B. C. D.
7.如图,点P是△ABC的边AC上一点,连接BP,以下条件中,不能判定△ABP∽△ACB的是( )
A.= B.= C.∠ABP=∠C D.∠APB=∠ABC
8.将抛物线y=﹣5x2+1向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为( )
A.y=﹣5(x+1)2﹣1 B.y=﹣5(x﹣1)2﹣1
C.y=﹣5(x+1)2+3 D.y=﹣5(x﹣1)2+3
9.已知反比例函数y=的图象经过点(1,1),则k的值为( )
A.﹣1 B.0 C.1 D.2
10.如图,抛物线y=ax2+bx+c的对称轴是直线x=1,下列结论:
①abc>0;②b2﹣4ac>0;③8a+c<0;④5a+b+2c>0,
正确的有( )
A.4个 B.3个 C.2个 D.1个
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知,则的值为 .
12.如图,直线y=x+m与双曲线y=相交于A,B两点,BC∥x轴,AC∥y轴,则△ABC面积的最小值为 .
13.如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长 .
14.如图,正方形ABCD中,点E是BC的中点,点F是CD上一点,分别以AE、AF为对称轴,折叠△ABE、△ADF,使得AB和AD与AG重合,连接BG交AE于点H,连接CG.
(1)HE:AH= ;
(2)S△AFE:S正方形ABCD= .
三、(本大题共2小题,每小题8分,满分16分)
15.若二次函数的图象的对称轴方程是x=,并且图象过A(0,﹣4)和B(4,0)
(1)求此二次函数图象上点A关于对称轴x=对称的点A′的坐标;
(2)求此二次函数的解析式.
16.如图,矩形OABC的两个顶点A,C分别在y轴和x轴上,边AB和BC与反比例函数y1=(x>0)和y2=(k>0,x>0)图象交于E,F和点H,G.AE:AF=2:3.
(1)求反比例函数y2的解析式;
(2)若点C的坐标为(8,0),求GH的长.
四、(本大题共2小题,每小题8分,满分16分)
17.已知抛物线y=(x﹣m)2﹣(x﹣m),其中m是常数.
(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x=.
①求该抛物线的函数解析式;
②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点.
18.已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.求证:△ABD∽△DCE.
五、(本大题共2小题,每小题10分,满分20分)
19.已知:△ABC中,∠C=90°,正方形DEFG,点D、G分别在AC、BC上,E、F在AB上;
(1)若AC=3,BC=4,求DG的长;
(2)如图2,四边形HPEQ、MNRF为正方形,设正方形HPEQ、MFRN、DEFG的边长分别为a、b、c,求证:a+b=c.
20.某商店经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天) 1≤x<50 50≤x≤90
售价(元/件) x+40 90
每天销量(件) 200﹣2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
六、(本题满分12分)
21.抛物线y=mx2﹣4m(m>0)与x轴交于A,B两点(A点在B点左边),与y轴交于C点,已知OC=2OA.求:
(1)A,B两点的坐标;
(2)抛物线的解析式.
七、(本题满分12分)
22.如图1,在△ABC中,AC=BC,点D,E,F分别是线段AC,BC,AD的中点,BF,ED的延长线交于点G.
(1)求证:AB=GD;
(2)如图2,连接GC,当CG=EG时,求的值.
八、(本题满分14分)
23.如图,在Rt△ABC中,CA=CB,M是AB的中点,点D在BM上,AE⊥CD,BF⊥
CD,垂足分别为E,F,连接EM.
①试证明:BF=CE;
②图中线段AE、CE与ME三者之间有何关系?并说明理由;
③求证:CF DM=BM DE.
参考答案
一、选择题(本大题共10小题,每小题4分,满分40分)(每小题都给出了A,B,C,D四个选项,其中只有一个是正确的)
1.若函数y=(a﹣1)x2+2x+a2﹣1是关于x的二次函数,则( )
A.a≠1 B.a≠﹣1 C.a=1 D.a=±1
【分析】利用二次函数定义进行解答即可.
解:由题意得:a﹣1≠0,
解得:a≠1,
故选:A.
2.关于二次函数y=2x2﹣8x,下列结论中正确的是( )
A.图象与x轴有两个交点
B.当x=2时,y有最大值﹣8
C.当x>1时,y随x的增大而增大
D.函数图象开口向下
【分析】根据函数解析式和二次函数的性质逐个判断即可.
解:∵二次函数y=2x2﹣8x=2(x﹣2)2﹣8,
∴抛物线的开口向上,对称轴为直线x=2,顶点为(2,﹣8),当x=2时,y有最小值﹣8,
∴当x>2时,y随x的增大而增大,
故B、C、D结论不正确,
∵y=2x2﹣8x=2x(x﹣4),
∴二次函数y=2x2﹣8x与x轴的交点为(0,0),(4,0),
故A正确;
故选:A.
3.若二次函数y=kx2﹣4x﹣2与x轴有两个不同的交点,则k的取值范围是( )
A.k>﹣2 B.k>﹣2且k≠0 C.k<2 D.k≥﹣2且k≠0
【分析】由抛物线与x轴有两个不同的交点可得出一元二次方程kx2﹣4x﹣2=0有两个不相等的解,由二次项系数非零及根的判别式Δ>0,即可得出关于k的一元一次不等式组,解之即可得出结论.
解:令y=0,则kx2﹣4x﹣2=0,
∵二次函数y=kx2﹣4x﹣2的图象与x轴有两个不同的交点,
∴一元二次方程kx2﹣4x﹣2=0有两个不相等的解,
∴,
解得:k>﹣2且k≠0.
故选:B.
4.对于反比例函数,下列结论:①图象分布在第二、四象限;②当x>0时,y随x的增大而增大;③图象经过点(1,﹣2);④若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则y1<y2,其中正确的是( )
A.①②③ B.②③④ C.①③④ D.①②④
【分析】根据题目中的函数解析式和反比例函数的性质,可以判断各个小题中的结论是否正确.
解:∵于反比例函数,
∴该函数的图象分布在第二、四象限,故①正确;
当x>0时,y随x的增大而增大,故②正确;
当x=1时,y=﹣2,故③正确;
若点A(x1,y1),B(x2,y2)都在图象上,且x1<x2,则点A和点B都在第二象限或都在第四象限时y1<y2,点A在第二象限,点B在第四象限时y1>y2,故④错误;
故选:A.
5.大自然是美的设计师,即使是一片小小的树叶,也蕴含着“黄金分割”,如图,P为AB的黄金分割点(AP>PB),则下列结论中正确的是( )
A.AB2=AP2+BP2 B.BP2=AP BA
C. D.
【分析】由黄金分割的定义得AP2=BP BA,==,即可求解.
解:∵P为AB的黄金分割点(AP>PB),
∴AP2=BP BA,==,故选项A、B、C不符合题意,选项D符合题意,
故选:D.
6.如图,在菱形ABCD中,点E,F分别在AB,CD上,且BE=2AE,DF=2CF,点G,H分别是AC的三等分点,则的值为( )
A. B. C. D.
【分析】由题意可证EG∥BC,HF∥AD,根据比例式即可求解.
解:∵BE=2AE,DF=2FC,
∴,
∵G、H分别是AC的三等分点,
∴,,
∴,
∴EG∥BC
∴,
同理可得HF∥AD,,
∴,
故选:A.
7.如图,点P是△ABC的边AC上一点,连接BP,以下条件中,不能判定△ABP∽△ACB的是( )
A.= B.= C.∠ABP=∠C D.∠APB=∠ABC
【分析】根据相似三角形的判定定理(①有两角分别相等的两三角形相似,②有两边的比相等,并且它们的夹角也相等的两三角形相似)逐个进行判断即可.
解:A、∵∠A=∠A,=,
∴△ABP∽△ACB,故本选项错误;
B、根据=和∠A=∠A不能判断△ABP∽△ACB,故本选项正确;
C、∵∠A=∠A,∠ABP=∠C,
∴△ABP∽△ACB,故本选项错误;
D、∵∠A=∠A,∠APB=∠ABC,
∴△ABP∽△ACB,故本选项错误;
故选:B.
8.将抛物线y=﹣5x2+1向左平移1个单位长度,再向下平移2个单位长度,所得到的抛物线为( )
A.y=﹣5(x+1)2﹣1 B.y=﹣5(x﹣1)2﹣1
C.y=﹣5(x+1)2+3 D.y=﹣5(x﹣1)2+3
【分析】直接利用二次函数图象与几何变换的性质分别平移得出答案.
解:将抛物线y=﹣5x2+1向左平移1个单位长度,得到y=﹣5(x+1)2+1,再向下平移2个单位长度,
所得到的抛物线为:y=﹣5(x+1)2﹣1.
故选:A.
9.已知反比例函数y=的图象经过点(1,1),则k的值为( )
A.﹣1 B.0 C.1 D.2
【分析】把点的坐标代入函数解析式得出方程,求出方程的解即可.
解:∵反比例函数y=的图象经过点(1,1),
∴代入得:2k﹣3=1×1,
解得:k=2,
故选:D.
10.如图,抛物线y=ax2+bx+c的对称轴是直线x=1,下列结论:
①abc>0;②b2﹣4ac>0;③8a+c<0;④5a+b+2c>0,
正确的有( )
A.4个 B.3个 C.2个 D.1个
【分析】根据抛物线的开口方向、对称轴、与坐标轴的交点判定系数符号及运用一些特殊点解答问题.
解:由抛物线的开口向下可得:a<0,
根据抛物线的对称轴在y轴右边可得:a,b异号,所以b>0,
根据抛物线与y轴的交点在正半轴可得:c>0,
∴abc<0,故①错误;
∵抛物线与x轴有两个交点,
∴b2﹣4ac>0,故②正确;
∵直线x=1是抛物线y=ax2+bx+c(a≠0)的对称轴,所以﹣=1,可得b=﹣2a,
由图象可知,当x=﹣2时,y<0,即4a﹣2b+c<0,
∴4a﹣2×(﹣2a)+c<0,
即8a+c<0,故③正确;
由图象可知,当x=2时,y=4a+2b+c>0;当x=﹣1时,y=a﹣b+c>0,
两式相加得,5a+b+2c>0,故④正确;
∴结论正确的是②③④3个,
故选:B.
二、填空题(本大题共4小题,每小题5分,满分20分)
11.已知,则的值为 1 .
【分析】设=k,根据比例的性质得出a=2k,b=3k,c=5k,再代入求出答案即可.
解:设=k,
则a=2k,b=3k,c=5k,
所以==1,
故答案为:1.
12.如图,直线y=x+m与双曲线y=相交于A,B两点,BC∥x轴,AC∥y轴,则△ABC面积的最小值为 6 .
【分析】方法一:根据双曲线y=过A,B两点,可设A(a,),B(b,),则C(a,).将y=x+m代入y=,整理得x2+mx﹣3=0,由于直线y=x+m与双曲线y=相交于A,B两点,所以a、b是方程x2+mx﹣3=0的两个根,根据根与系数的关系得出a+b=﹣m,ab=﹣3,那么(a﹣b)2=(a+b)2﹣4ab=m2+12.再根据三角形的面积公式得出S△ABC=AC BC=m2+6,利用二次函数的性质即可求出当m=0时,△ABC的面积有最小值6.
方法二:先根据△ABC为等腰直角三角形,得出S△ABC=AC BC=AB2,AB最小时,面积最小,即m=0时面积最小,联立方程,得出A,B的坐标,即可求得AB的长,进而得出三角形面积的最小值.
解:方法一:
设A(a,),B(b,),则C(a,).
将y=x+m代入y=,得x+m=,
整理,得x2+mx﹣3=0,
则a+b=﹣m,ab=﹣3,
∴(a﹣b)2=(a+b)2﹣4ab=m2+12.
∵S△ABC=AC BC
=(﹣)(a﹣b)
= (a﹣b)
=(a﹣b)2
=(m2+12)
=m2+6,
∴当m=0时,△ABC的面积有最小值6.
故答案为6.
方法二:
因为y=x+m斜率为1,且BC∥x轴,AC∥y轴
∴∠ABC=∠BAC=45°
∴△ABC为等腰直角三角形
∴AC=BC=AB
∴S△ABC=AC BC=AB2
当AB最小时,m=0,直线为y=x
联立方程,解得或
∴A(,),B(﹣,﹣)
AB=×2=2
∴S△ABC最小=×4×6=6
故答案为6.
13.如图,在△ABC中,BC的垂直平分线MN交AB于点D,CD平分∠ACB.若AD=2,BD=3,则AC的长 .
【分析】证出∠ACD=∠DCB=∠B,证明△ACD∽△ABC,得出=,即可得出结果.
解:∵BC的垂直平分线MN交AB于点D,
∴CD=BD=3,
∴∠B=∠DCB,AB=AD+BD=5,
∵CD平分∠ACB,
∴∠ACD=∠DCB=∠B,
∵∠A=∠A,
∴△ACD∽△ABC,
∴=,
∴AC2=AD×AB=2×5=10,
∴AC=.
故答案为:.
14.如图,正方形ABCD中,点E是BC的中点,点F是CD上一点,分别以AE、AF为对称轴,折叠△ABE、△ADF,使得AB和AD与AG重合,连接BG交AE于点H,连接CG.
(1)HE:AH= 1:4 ;
(2)S△AFE:S正方形ABCD= 5:12 .
【分析】(1)根据翻折的性质得到∠GHE=∠BHE=90°,再根据∠HEB=∠BEA,从而证明△HEB∽△BEA,得出,设正方形边长为2x,则BE=x,AB=2x,由勾股定理求出AE,从而求出HE和AH,得出结论;
(2)由S△AFE=(S正方形ABCD﹣S△FCE),正方形ABCD的边长为2,FG=DF=x,则EF=1+x,CF=2﹣x,由勾股定理求出x即可.
解:(1)∵AE为对称轴,
∴△AEG≌△AEB,BG⊥AE,
∴∠GHE=∠BHE=90°,
又∵∠HEB=∠BEA,
∴△HEB∽△BEA,
∴=,
在正方形ABCD中,设边长为2x,
则BE=x,AB=2x,
∴AE===x,
∴HE===x,
∴AH=AE﹣HE=x﹣x=x,
∴HE:AH=x:x=1:4.
故答案为:1:4;
(2)设正方形ABCD的边长为2,则S正方形ABCD=4,
∵S△AFE=(S正方形ABCD﹣S△FCE),CE=BE=GE=1,
设FG=DF=x,
则EF=1+x,CF=2﹣x,
在△EFC中,
∵EF2=CE2+CF2,
∴(1+x)2=(2﹣x)2+1,
解得:x=,
∴CE=2﹣x=,
∴S△CFE=×CE×CF=××1=,
∴S△AFE=×(4﹣)=,
∴S△AFE:S正方形ABCD=:4=5:12.
故答案为:5:12.
三、(本大题共2小题,每小题8分,满分16分)
15.若二次函数的图象的对称轴方程是x=,并且图象过A(0,﹣4)和B(4,0)
(1)求此二次函数图象上点A关于对称轴x=对称的点A′的坐标;
(2)求此二次函数的解析式.
【分析】(1)直接利用对称性求解即可;
(2)利用待定系数法把A(0,﹣4)和B(4,0),即对称轴x=代入解析式,解三元一次方程组可得y=x2﹣3x﹣4.
解:(1)A′(3,﹣4);
(2)设此二次函数的解析式为y=ax2+bx+c,
由题意,得,
解得.
∴y=x2﹣3x﹣4.
16.如图,矩形OABC的两个顶点A,C分别在y轴和x轴上,边AB和BC与反比例函数y1=(x>0)和y2=(k>0,x>0)图象交于E,F和点H,G.AE:AF=2:3.
(1)求反比例函数y2的解析式;
(2)若点C的坐标为(8,0),求GH的长.
【分析】(1)设E(a,b),根据已知条件求得F(a,b),分别代入解析式得出ab=4,a b=k,从而求得k=6,D得出反比例函数y2的解析式;
(2)把x=8分别代入y1=和y2=,即可求得CG、CH的值,然后根据GH=CG﹣CH即可求得.
解:(1)设E(a,b),
∴AE=a,
∵AE:AF=2:3.
∴AF=a,
∴F(a,b),
∵E是反比例函数y1=(x>0)上的点,
∴ab=4,
∵F是反比例函数(k>0,x>0)图象上的点,
∴a b=k,
∴k=×4=6,
∴反比例函数y2的解析式为y2=.
(2)把x=8分别代入y1=和y2=得,y1=和y2=,
∴CH=,CG=,
∴GH=CG﹣CH=.
四、(本大题共2小题,每小题8分,满分16分)
17.已知抛物线y=(x﹣m)2﹣(x﹣m),其中m是常数.
(1)求证:不论m为何值,该抛物线与x轴一定有两个公共点;
(2)若该抛物线的对称轴为直线x=.
①求该抛物线的函数解析式;
②把该抛物线沿y轴向上平移多少个单位长度后,得到的抛物线与x轴只有一个公共点.
【分析】(1)先把抛物线解析式化为一般式,再计算△的值,得到△=1>0,于是根据Δ=b2﹣4ac决定抛物线与x轴的交点个数即可判断不论m为何值,该抛物线与x轴一定有两个公共点;
(2)①根据对称轴方程得到=﹣=,然后解出m的值即可得到抛物线解析式;
②根据抛物线的平移规律,设抛物线沿y轴向上平移k个单位长度后,得到的抛物线与x轴只有一个公共点,则平移后抛物线解析式为y=x2﹣5x+6+k,再利用抛物线与x轴的只有一个交点得到△=52﹣4(6+k)=0,
然后解关于k的方程即可.
【解答】(1)证明:y=(x﹣m)2﹣(x﹣m)=x2﹣(2m+1)x+m2+m,
∵△=(2m+1)2﹣4(m2+m)=1>0,
∴不论m为何值,该抛物线与x轴一定有两个公共点;
(2)解:①∵x=﹣=,
∴m=2,
∴抛物线解析式为y=x2﹣5x+6;
②设抛物线沿y轴向上平移k个单位长度后,得到的抛物线与x轴只有一个公共点,则平移后抛物线解析式为y=x2﹣5x+6+k,
∵抛物线y=x2﹣5x+6+k与x轴只有一个公共点,
∴△=52﹣4(6+k)=0,
∴k=,
即把该抛物线沿y轴向上平移个单位长度后,得到的抛物线与x轴只有一个公共点.
18.已知:如图,△ABC中,∠BAC=90°,AB=AC=1,点D是BC边上的一个动点(不与B,C点重合),∠ADE=45°.求证:△ABD∽△DCE.
【分析】先判断△ABC为等腰直角三角形得到∠B=∠C=45°,再利用三角形内角和得到∠1+∠2=135°,利用平角定义得到∠2++∠3=135°,则∠1=∠3,于是可根据有两组角对应相等的两个三角形相似得到结论.
【解答】证明:∵∠BAC=90°,AB=AC=1,
∴△ABC为等腰直角三角形,
∴∠B=∠C=45°,
∴∠1+∠2=180°﹣∠B=135°,
∵∠ADE=45°,
∴∠2+∠3=135°,
∴∠1=∠3,
∵∠B=∠C,
∴△ABD∽△DCE.
五、(本大题共2小题,每小题10分,满分20分)
19.已知:△ABC中,∠C=90°,正方形DEFG,点D、G分别在AC、BC上,E、F在AB上;
(1)若AC=3,BC=4,求DG的长;
(2)如图2,四边形HPEQ、MNRF为正方形,设正方形HPEQ、MFRN、DEFG的边长分别为a、b、c,求证:a+b=c.
【分析】(1)过C作CM⊥BA于M,交DG于N,由勾股定理求出AB的长,再由三角形面积计算公式即可求出CM的长,由DG=GF=EF=DE=MN,DG∥BA,得△CDG∽△CAB,再根据相似三角形的性质列出比例式即可求解;
(2)利用两个角相等,可证明△NMG∽△DQH,得,代入即可得出a,b,c的关系.
【解答】(1)解:过C作CM⊥BA于M,交DG于N,
∵△ABC是直角三角形,∠ACB=90°,CB=4,AC=3,
∴BA==5,
由三角形面积公式得:AC×BC=AB×CM,
∵CB=4,AC=3,BA=5,
∴CM=2.4,
∵四边形DEFG是正方形,
∴DG=GF=EF=DE=MN,DG∥BA,
∴△CDG∽△CAB,
∴=,
∴,
∴DG=;
(2)证明:∵∠MGN+∠CGD=90°,∠CDG+∠CGD=90°,
∴∠MGN=∠CDG,
同理,∠DHQ=∠CDG,
∴∠MGN=∠DHQ,
∵∠NMG=∠DQH,
∴△NMG∽△DQH,
∴,即,
∴ab=c2﹣ac﹣bc+ab,
∴0=c2﹣ac﹣bc,
即c2=ac+bc,
∵c>0,
∴a+b=c.
20.某商店经过市场调查,整理出某种商品在第x(1≤x≤90)天的售价与销量的相关信息如下表:
时间x(天) 1≤x<50 50≤x≤90
售价(元/件) x+40 90
每天销量(件) 200﹣2x
已知该商品的进价为每件30元,设销售该商品的每天利润为y元.
(1)求出y与x的函数关系式;
(2)问销售该商品第几天时,当天销售利润最大,最大利润是多少?
【分析】(1)分成1≤x<50和50≤x≤90两种情况进行讨论,利用:利润=每件的利润×销售的件数,即可求得函数的解析式;
(2)结合(1)得到的两个解析式,结合二次函数与一次函数的性质分别求得最值,然后两种情况下取最大的即可.
解:(1)当1≤x<50时,y=(200﹣2x)(x+40﹣30)=﹣2x2+180x+2000,
当50≤x≤90时,
y=(200﹣2x)(90﹣30)=﹣120x+12000,
综上所述:y=;
(2)当1≤x<50时,二次函数开口下,二次函数对称轴为直线x=45,
当x=45时,y最大=﹣2×452+180×45+2000=6050,
当50≤x≤90时,y随x的增大而减小,
当x=50时,y最大=6000,
综上所述,该商品第45天时,当天销售利润最大,最大利润是6050元;
六、(本题满分12分)
21.抛物线y=mx2﹣4m(m>0)与x轴交于A,B两点(A点在B点左边),与y轴交于C点,已知OC=2OA.求:
(1)A,B两点的坐标;
(2)抛物线的解析式.
【分析】(1)通过解方程mx2﹣4m=0可得A、B点的坐标;
(2)先利用OA=2得到OC=4,所以|﹣4m|=4,然后求出满足条件的m的值,从而得到抛物线解析式.
解:(1)当y=0时,mx2﹣4m=0,即x2﹣4=0,解得x1=2,x2=﹣2,
∴A(﹣2,0),B(2,0);
(2)当x=0时,y=mx2﹣4m=﹣4m,
∴C(0,﹣4m),
∵OA=2,
∴OC=2OA=4,
∴|﹣4m|=4,解得m=1或m=﹣1,
∵m>0,
∴m=1,
∴抛物线解析式为y=x2﹣4.
七、(本题满分12分)
22.如图1,在△ABC中,AC=BC,点D,E,F分别是线段AC,BC,AD的中点,BF,ED的延长线交于点G.
(1)求证:AB=GD;
(2)如图2,连接GC,当CG=EG时,求的值.
【分析】(1)由题意可知DE是△ABC的中位线,从而可知EG∥AB,又点F为线段AD的中点,所以AF=DF,然后证明△ABF≌△DGF(ASA),由全等三角形的性质即可得出AB=GD.
(2)由条件可知DE=AB,EG=AB,然后利用DE∥AB,证明△GEC∽△CBA,从而求出的值.
【解答】(1)证明:∵点D,E,F分别是线段AC,BC,AD的中点,
∴DE为△ABC的中位线,AF=DF,
∴ED∥AB,
∴∠A=∠GDF,
在△ABF和△DGF中,
∴△ABF≌△DGF(ASA),
∴AB=GD;
(2)解:∵D、E为AC、BC中点,
∴AC=2DC,BC=2CE,
∵AC=BC,
∴AC=2CE,∠A=∠ABC,
∵EG∥AB,
∴∠GEC=∠ABC=∠EDC=∠A,
∵GE=GC,
∴∠GCE=∠GEC=∠EDC=∠A,
∴△CDE∽△GCE,
∴,
∴EC2=ED GE,
∵DE为△ABC的中位线,
∴DE=AB,
∴GE=DE+GD=AB,
∴CE===AB,
∵AC=2CE,
∴AC=2CE=2×AB,
∴.
八、(本题满分14分)
23.如图,在Rt△ABC中,CA=CB,M是AB的中点,点D在BM上,AE⊥CD,BF⊥
CD,垂足分别为E,F,连接EM.
①试证明:BF=CE;
②图中线段AE、CE与ME三者之间有何关系?并说明理由;
③求证:CF DM=BM DE.
【分析】①证明△BCF≌△CAE,根据等腰三角形的性质即可得到BF=CE;
②连接FM,CM,证明△BFM≌△CEM,从而判断△EMF为等腰直角三角形,得到EF=EM,即可得出AE﹣CE=ME;
③证明△CDM∽ADE,得到对应边成比例,结合BM=CM,AE=CF即可得出结论.
【解答】①证明:∵△ABC是直角三角形,
∠ACB=90°,
∴∠BCF+∠ACE=90°,
∵∠BCF+∠CBF=90°,
∴∠ACE=∠CBF,
又∵∠BFD=90°=∠AEC,AC=BC,
∴△BCF≌△CAE(AAS),
∴BF=CE;
②解:AE﹣CE=ME,
理由:由①得:△BCF≌△CAE,
∴AE=CF,BF=CE,
∴AE﹣CE=CF﹣CE=EF,
连接FM,CM,
∵点M是AB中点,
∴CM=AB=BM=AM,CM⊥AB,
在△BDF和△CDM中,∠BFD=∠CMD,∠BDF=∠CDM,
∴∠DBF=∠DCM,
又BM=CM,BF=CE,
∴△BFM≌△CEM(SAS),
∴FM=EM,∠BMF=∠CME,
∵∠BMC=90°,
∴∠EMF=90°,即△EMF为等腰直角三角形,
∴EF=EM,
∵AE﹣CE=EF,
∴AE﹣CE=EM;
③证明:连接CM,
∵∠CDM=∠ADE,∠CMD=∠AED=90°,
∴△CDM∽△ADE,
∴,
∵BM=CM,AE=CF,
∴,
∴CF DM=BM DE.
同课章节目录
