2021-2022学年北师大版九年级数学下册 1.5三角函数的应用 同步达标测评 (word版含答案)
文档属性
| 名称 | 2021-2022学年北师大版九年级数学下册 1.5三角函数的应用 同步达标测评 (word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 471.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 21:28:59 | ||
图片预览


文档简介
2021-2022学年北师大版九年级数学下册《1.5三角函数的应用》同步达标测评(附答案)
一.选择题(共4小题,满分20分)
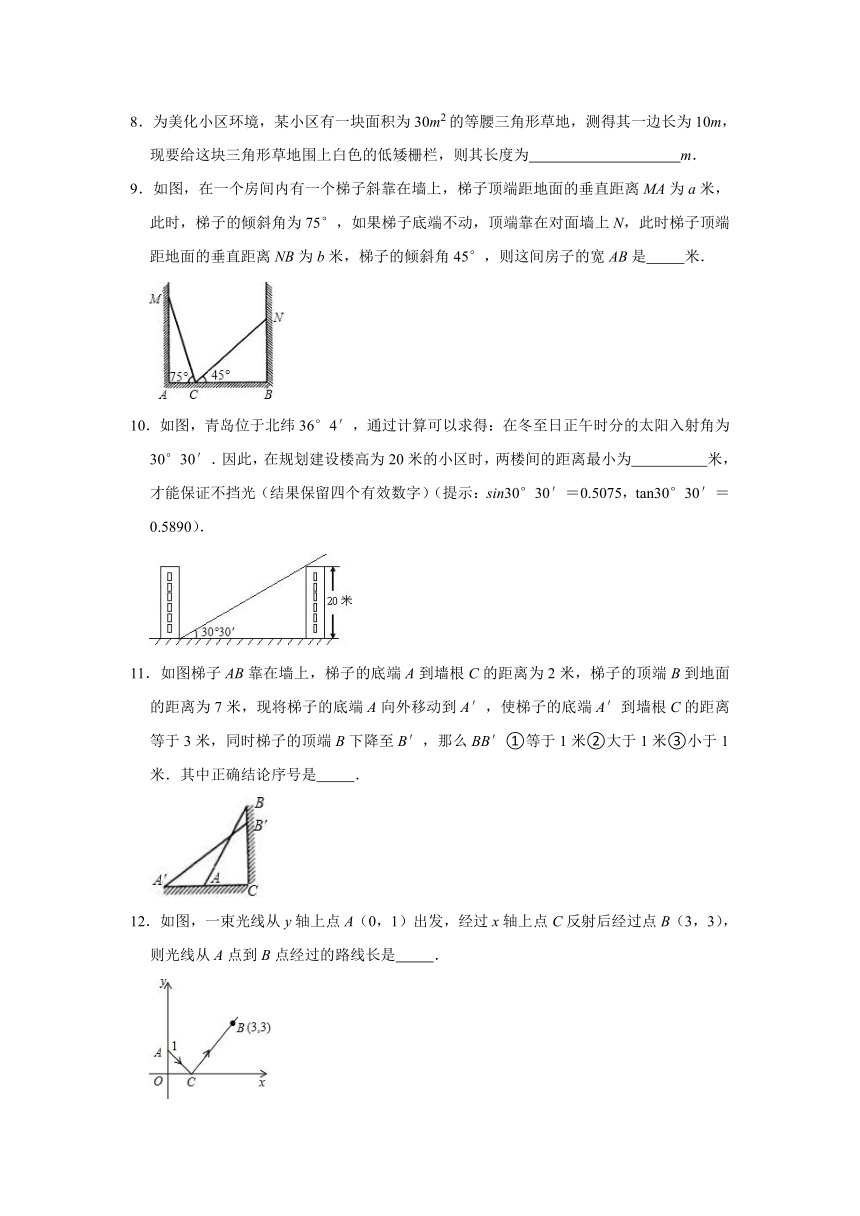
1.如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=18 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为( )
A.24m B.22m C.20m D.18m
2.如图,矩形草坪ABCD中,AD=10m,AB=10m.现需要修一条由两个扇环构成的便道HEFG,扇环的圆心分别是B、D.若便道的宽为1m,则这条便道的面积大约是( )(精确到0.1m2)
A.9.5m2 B.10.0m2 C.10.5m2 D.11.0m2
3.如图所示,CD是平面镜,光线从A点出发经CD上的E点反射后到达B点,若入射角为α,AC⊥CD,BD⊥CD,垂足分别为C,D,且AC=3,BD=6,CD=11,则tanα的值是( )
A. B. C. D.
4.如图,在一个房间内,有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为a米,此时梯子的倾斜角为75°,如果梯子的底端不动,顶端靠在对面墙上,此时梯子的顶端距地面的垂直距离NB为b米,梯子的倾斜角为45°,则这间房子的宽AB为( )
A.米 B.米 C.b米 D.a米
二.填空题(共8小题,满分32分)
5.如图是一山谷的横断面示意图,宽AA′为15m,用曲尺(两直尺相交成直角)从山谷两侧测量出OA=1m,OB=3m,O′A′=0.5m,O′B′=3m(点A,O,O′A′在同一条水平线上),则该山谷的深h为 m.
6.小敏想知道校园内一棵大树的高(如图),她测得CB=10米,∠ACB=50°,请你帮她算出树高AB约为 米.(注:①树垂直于地面;②供选用数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)
7.如图,我校为了筹备校园艺术节,要在通往舞台的台阶上铺上红色地毯.如果地毯的宽度恰好与台阶的宽度一致,台阶的侧面如图所示,台阶的坡角为30°,∠BCA=90°,台阶的高BC为2米,那么请你帮忙算一算需要 米长的地毯恰好能铺好台阶.(结果精确到0.1m,取=1.414,=1.732).
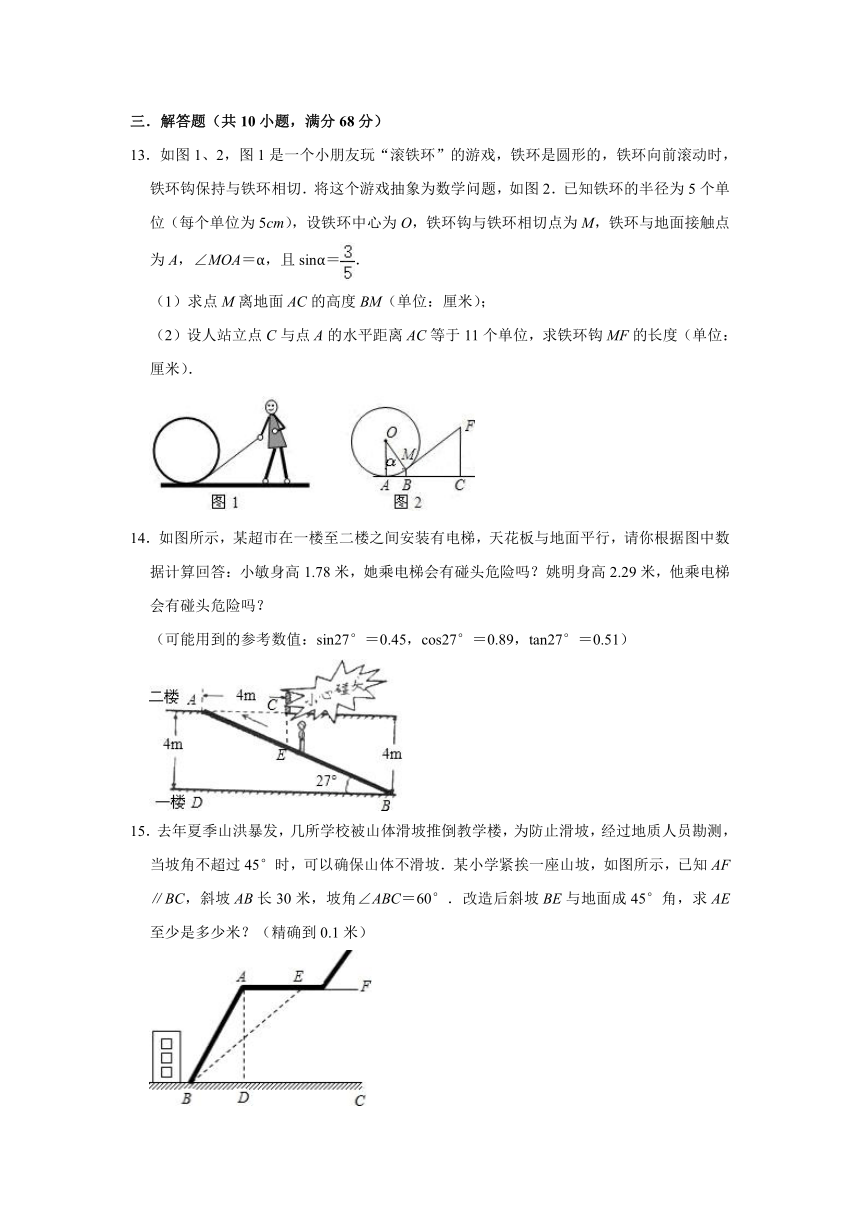
8.为美化小区环境,某小区有一块面积为30m2的等腰三角形草地,测得其一边长为10m,现要给这块三角形草地围上白色的低矮栅栏,则其长度为 m.
9.如图,在一个房间内有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为a米,此时,梯子的倾斜角为75°,如果梯子底端不动,顶端靠在对面墙上N,此时梯子顶端距地面的垂直距离NB为b米,梯子的倾斜角45°,则这间房子的宽AB是 米.
10.如图,青岛位于北纬36°4′,通过计算可以求得:在冬至日正午时分的太阳入射角为30°30′.因此,在规划建设楼高为20米的小区时,两楼间的距离最小为 米,才能保证不挡光(结果保留四个有效数字)(提示:sin30°30′=0.5075,tan30°30′=0.5890).
11.如图梯子AB靠在墙上,梯子的底端A到墙根C的距离为2米,梯子的顶端B到地面的距离为7米,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根C的距离等于3米,同时梯子的顶端B下降至B′,那么BB′①等于1米②大于1米③小于1米.其中正确结论序号是 .
12.如图,一束光线从y轴上点A(0,1)出发,经过x轴上点C反射后经过点B(3,3),则光线从A点到B点经过的路线长是 .
三.解答题(共10小题,满分68分)
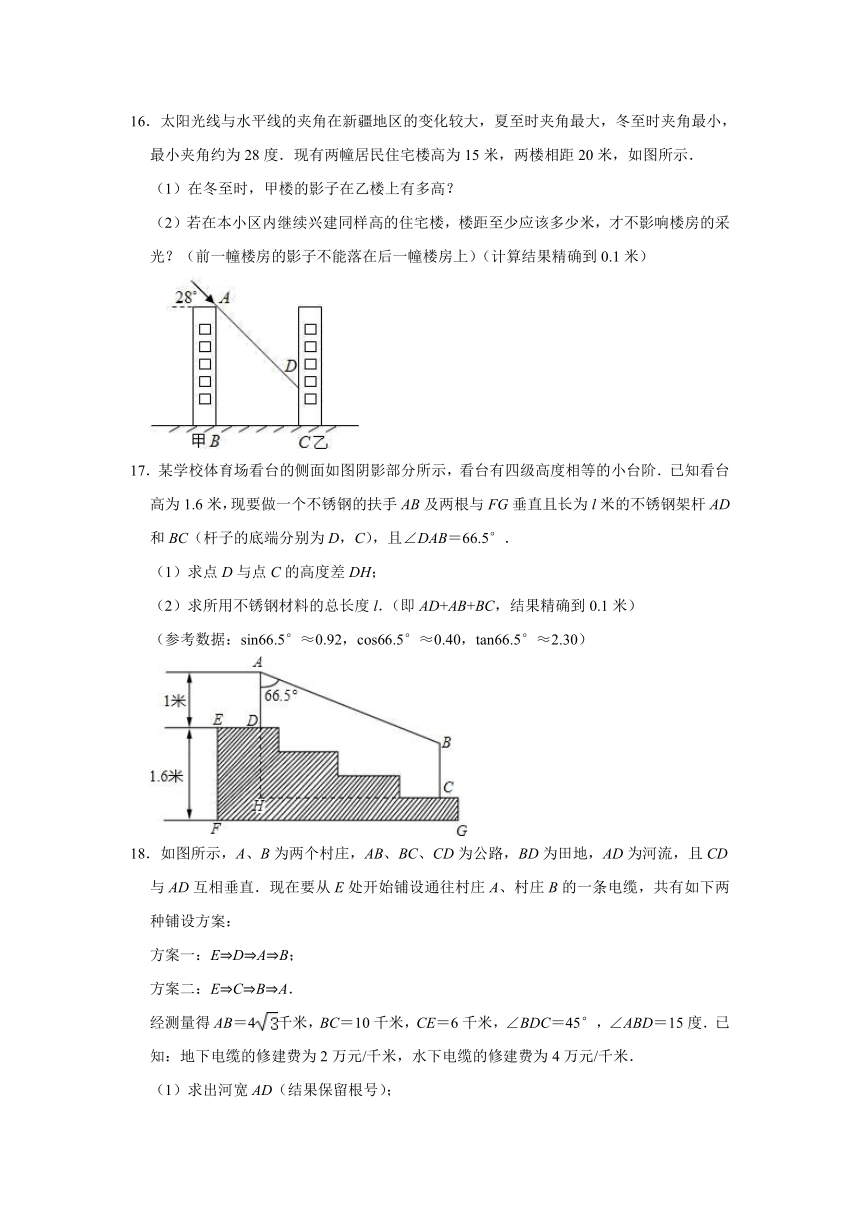
13.如图1、2,图1是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图2.已知铁环的半径为5个单位(每个单位为5cm),设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=.
(1)求点M离地面AC的高度BM(单位:厘米);
(2)设人站立点C与点A的水平距离AC等于11个单位,求铁环钩MF的长度(单位:厘米).
14.如图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行,请你根据图中数据计算回答:小敏身高1.78米,她乘电梯会有碰头危险吗?姚明身高2.29米,他乘电梯会有碰头危险吗?
(可能用到的参考数值:sin27°=0.45,cos27°=0.89,tan27°=0.51)
15.去年夏季山洪暴发,几所学校被山体滑坡推倒教学楼,为防止滑坡,经过地质人员勘测,当坡角不超过45°时,可以确保山体不滑坡.某小学紧挨一座山坡,如图所示,已知AF∥BC,斜坡AB长30米,坡角∠ABC=60°.改造后斜坡BE与地面成45°角,求AE至少是多少米?(精确到0.1米)
16.太阳光线与水平线的夹角在新疆地区的变化较大,夏至时夹角最大,冬至时夹角最小,最小夹角约为28度.现有两幢居民住宅楼高为15米,两楼相距20米,如图所示.
(1)在冬至时,甲楼的影子在乙楼上有多高?
(2)若在本小区内继续兴建同样高的住宅楼,楼距至少应该多少米,才不影响楼房的采光?(前一幢楼房的影子不能落在后一幢楼房上)(计算结果精确到0.1米)
17.某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶.已知看台高为1.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长为l米的不锈钢架杆AD和BC(杆子的底端分别为D,C),且∠DAB=66.5°.
(1)求点D与点C的高度差DH;
(2)求所用不锈钢材料的总长度l.(即AD+AB+BC,结果精确到0.1米)
(参考数据:sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30)
18.如图所示,A、B为两个村庄,AB、BC、CD为公路,BD为田地,AD为河流,且CD与AD互相垂直.现在要从E处开始铺设通往村庄A、村庄B的一条电缆,共有如下两种铺设方案:
方案一:E D A B;
方案二:E C B A.
经测量得AB=4千米,BC=10千米,CE=6千米,∠BDC=45°,∠ABD=15度.已知:地下电缆的修建费为2万元/千米,水下电缆的修建费为4万元/千米.
(1)求出河宽AD(结果保留根号);
(2)求出公路CD的长;
(3)哪种方案铺设电缆的费用低?请说明你的理由.
19.如图是一座人行天桥的示意图,天桥的高是10米,坡面的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面的倾斜角为30°,若新坡角下需留3米的人行道,问离原坡角10米的建筑物是否需要拆除?(参考数据:≈1.414,≈1.732.)
20.已知:如图,A、B、C三个村庄在一条东西走向的公路沿线上,AB=2km.在B村的正北方向有一个D村,测得∠DAB=45°,∠DCB=28°.今将△ACD区域进行规划,除其中面积为0.5km2的水塘外,准备把剩余的一半作为绿化用地,试求绿化用地的面积.(结果精确到0.1km2,sin28°=0.4695,cos28°=0.8829,tan28°=0.5317,cot28°=1.88.8)
21.如图,在一次龙卷风中,一棵大树在离地面若干千米处折断倒下,B为折断处最高点,树顶A落在离树根C的12米处,测得∠BAC=48°,求BC的长.(借助计算器,精确到0.1米)
22.苏州的虎丘塔塔身倾斜,却历经千年而不倒,被誉为“中国第一斜塔”.如图,BC是过塔底中心B的铅垂线.AC是塔顶A偏离BC的距离.据测量,约为2.34米,倾角约为2°48′,求虎丘塔塔身AB的长度.(精确到0.1米)
参考答案
一.选择题(共4小题,满分20分)
1.解:过D作DF⊥CD,交AE于点F,过F作FG⊥AB,垂足为G.
由题意得:.
∴DF=DE×1.6÷2=14.4(m).
∴GF=BD=CD=6m.
又∵.
∴AG=1.6×6=9.6(m).
∴AB=14.4+9.6=24(m).
答:铁塔的高度为24m.
故选:A.
2.解:∵四边形ABCD为矩形,
∴△ADB为直角三角形,
又∵AD=10,AB=10,
∴BD==20,
又∵cos∠ADB==,
∴∠ADB=60°.
又矩形对角线互相平分且相等,便道的宽为1m,
所以每个扇环都是圆心角为30°,且外环半径为10.5,内环半径为9.5.
∴每个扇环的面积为=.
∴当π取3.14时整条便道面积为=10.4666≈10.5m2.
便道面积约为10.5m2.
故选:C.
3.解:因为AC、BD、法线均和镜面垂直,
所以∠A=∠B=α,
而由已知得△ACE∽△BDE,
所以=即=
∴,
在三角形ACE中tanA====tanα.
故选:D.
4.解:过N点作MA垂线,垂足点D,连接NM.
设梯子底端为C点,AB=x,且AB=ND=x.
∴△BNC为等腰直角三角形,
∴180°﹣45°﹣75°=60°
∴△CNM为等边三角形,梯子长度相同
∵∠NCB=45°,
∴∠DNC=45°,
∴∠MND=60°﹣45°=15°,
∴cos15°=,
又∵∠MCA=75°,
∴∠AMC=15°,
∴cos15°=,
故可得:=.
∵△CNM为等边三角形,
∴NM=CM.
∴x=MA=a.
故选:D.
二.填空题(共8小题,满分32分)
5.解:设A、A′到谷底的水平距离为AC=m,A′C=n.
∴m+n=15.
根据题意知,OB∥CD∥O′B′.
∵OA=1,OB=3,O′A′=0.5,O′B′=3.
∴==3,==6.
∴(+)×h=15.
解得h=30(m).
6.解:由题可知,在Rt△ABC中,tan50°=AB:BC,
∴AB=tan50°×BC≈1.2×10=12(米).
7.解:在Rt△ABC中,∠A=30°,BC=2,∠C=90°.
∵tanA=,∴=2.
∴AC+BC=2+2≈2×1.73+2=5.46≈5.5(m).
即地毯的长度至少需5.5m.
8.解:(1)如图1,当底边BC=10m时,
由于S=30m2,所以高AD=6m,
此时AB=AC==(m),
所以周长=(2+10)m;
(2)①当△ABC是锐角三角形时,如图2,当AB=AC=10m时,高CE=6,此时AE=8m,BE=2m,在Rt△BEC中,BC=2m,
此时周长=(20+2)m.
②当△ABC是钝角三角形时,如图3,设BD=xm,AD=hm,
则在Rt△ABD中,×2x×h=30,
xh=30,
,解得或(舍去),
故△ABC是钝角三角形时,△ABC的周长=2×10+3=(20+6)(m),
故填空答案:2+10或20+2或20+6.
9.解:过N点作MA垂线,垂足点D,连接NM.
由题意得AB=ND,△CNM为等边三角形(180﹣45﹣75=60°,梯子长度相同),
∵∠ACM=75°,
∴∠AMC=15°.
∴∠AMN=75°,
在△MND中,ND=MN×sin75°,
在△MAC中,AM=MC×sin75°,
∵MN=MC,
∴ND=MA=a.
故答案为a.
10.解:由题意可知,光线,楼和地面构成一个直角三角形.
∴tan30°30′=,
所以楼间距=,
即楼间距=≈33.96(米).
11.解:由勾股定理得:梯子AB=,CB′=.
∴BB′=7﹣<1,故选③.
12.解:A关于x轴的对称点A′坐标是(0,﹣1)连接A′B,交x轴于点C,
作DB∥A′A,A′D∥OC,交DB于D,
故光线从点A到点B所经过的路程A′B===5.
三.解答题(共10小题,满分68分)
13.解:过M作与AC平行的直线,与OA、FC分别相交于H、N.
(1)在Rt△OHM中,∠OHM=90°,OM=5,
HM=OM×sinα=3,
所以OH=4,
MB=HA=5﹣4=1,
1×5=5cm.
所以铁环钩离地面的高度为5cm;
(2)∵铁环钩与铁环相切,
∴∠MOH+∠OMH=∠OMH+∠FMN=90°,∠FMN=∠MOH=α,
∴=sinα=,
∴FN=FM,
在Rt△FMN中,∠FNM=90°,MN=BC=AC﹣AB=11﹣3=8.
∵FM2=FN2+MN2,
即FM2=(FM)2+82,
解得:FM=10,
10×5=50(cm).
∴铁环钩的长度FM为50cm.
14.解:姚明乘此电梯会有碰头危险.(1分)
理由:由题意可知:AC∥BD,
∴∠CAB=∠ABD=27°.(2分)
过点C作CE⊥AC交AB于点E,(3分)
在Rt△ACE中,tan∠CAE=,(4分)
∴CE=AC tan∠CAE=4×tan27°≈4×0.51=2.04(米)<2.29(米).
∴姚明乘此电梯会有碰头危险.
∵2.04>1.78,
∴小敏乘此电梯不会有碰头危险.
15.解:在Rt△ADB中,AB=30米∠ABC=60°
AD=AB sin∠ABC=30×sin60°=15≈25.98≈26.0(米),
DB=AB cos∠ABC=30×cos60°=15米.
连接BE,过E作EN⊥BC于N
∵AE∥BC∴四边形AEND是矩形NE=AD≈26米
在Rt△ENB中,由已知∠EBN≤45°,
当∠EBN=45°时,BN=EN=26.0米
∴AE=DN=BN﹣BD=26.0﹣15=11米
答:AE至少是11.0米.
16.解:(1)如图所示,
作DE⊥AB,垂足为E,
由题意可知∠ADE=28°,DE=BC=20,
在Rt△ADE中,tan∠ADE=,
AE=DE tan∠ADE=20 tan28°≈10.6,
则DC=EB=AB﹣AE=15﹣10.6=4.4.
即冬至时甲楼的影子在乙楼上约4.4米高.
(2)若要不影响要房间的采光,如图所示在Rt△ABC中,AB=15,∠C=28°,
BC=≈28.2.
答:楼距至少28.2米,才不影响楼房的采光.
17.解:(1)DH=1.6×=1.2(m);
(2)过B作BM⊥AH于M,则四边形BCHM是矩形.
∴MH=BC=1(m),
∴AM=AH﹣MH=1+1.2﹣1=1.2(m).
在Rt△AMB中,∠A=66.5°.
∴AB=(m).
∴l=AD+AB+BC≈1+3.0+1=5.0(m).
答:点D与点C的高度差DH为1.2m;所用不锈钢材料的总长度约为5.0m.
18.解:(1)过点B作BF⊥AD,交DA的延长线于点F.
由题意得:∠BAF=∠ABD+∠ADB=15°+45°=60°,
在Rt△BFA中,BF=ABsin60°=4×=6(千米),
AF=ABcos60°=4×=2(千米).
∵CD⊥AD,∠BDC=45°,
∴∠BDF=45°,
在Rt△BFD中,∵∠BDF=45°,
∴DF=BF=6千米.
∴AD=DF﹣AF=(6﹣2)(千米).
即河宽AD为(6﹣2)千米;
(2)过点B作BG⊥CD于G,易证四边形BFDG是正方形,
∴BG=BF=6千米.
在Rt△BGC中,=8(千米),
∴CD=CG+GD=14千米.
即公路CD的长为14千米;
(3)方案一的铺设电缆费用低.
由(2)得DE=CD﹣CE=8千米.
∴方案一的铺设费用为:2(DE+AB)+4AD=40万元,
方案二的铺设费用为:2(CE+BC+AB)=(32+8)万元.
∵40<32+8,
∴方案一的铺设电缆费用低.
19.解:∵∠CAB=45°.
∴AB=BC=10.
∵∠CDB=30°.
∴BD=10.
∴AD=10﹣10≈7.32.(7分)
∵7.32+3>10.
答:离原坡角10米的建筑物需要拆除.(10分)
20.解:在Rt△ABD中,
∵∠ABD=90°,∠BAD=45°,∠ADB=45°,
∴BD=AB=2km,
在Rt△BCD中,
∵cot∠BCD=,∠DCB=28°,
∴BC=BD cot∠BCD=2cot28°(km),
∴S△ACD=AC BD=(2+2cot28°)(km2).
∴S绿地=(2+2cot28°)≈2.6(km2).
答:绿化用地的面积为2.6km2.
21.解:在直角△ABC中,tan∠BAC=
∴BC=AC tan48°=12tan48°≈13.3米.
22.解:在Rt△ABC中,∵sin∠ABC=
∴
=
≈47.9.
答:虎丘塔塔身AB长约为47.9m.
一.选择题(共4小题,满分20分)
1.如图,在斜坡的顶部有一铁塔AB,B是CD的中点,CD是水平的,在阳光的照射下,塔影DE留在坡面上.已知铁塔底座宽CD=12 m,塔影长DE=18 m,小明和小华的身高都是1.6m,同一时刻,小明站在点E处,影子在坡面上,小华站在平地上,影子也在平地上,两人的影长分别为2m和1m,那么塔高AB为( )
A.24m B.22m C.20m D.18m
2.如图,矩形草坪ABCD中,AD=10m,AB=10m.现需要修一条由两个扇环构成的便道HEFG,扇环的圆心分别是B、D.若便道的宽为1m,则这条便道的面积大约是( )(精确到0.1m2)
A.9.5m2 B.10.0m2 C.10.5m2 D.11.0m2
3.如图所示,CD是平面镜,光线从A点出发经CD上的E点反射后到达B点,若入射角为α,AC⊥CD,BD⊥CD,垂足分别为C,D,且AC=3,BD=6,CD=11,则tanα的值是( )
A. B. C. D.
4.如图,在一个房间内,有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为a米,此时梯子的倾斜角为75°,如果梯子的底端不动,顶端靠在对面墙上,此时梯子的顶端距地面的垂直距离NB为b米,梯子的倾斜角为45°,则这间房子的宽AB为( )
A.米 B.米 C.b米 D.a米
二.填空题(共8小题,满分32分)
5.如图是一山谷的横断面示意图,宽AA′为15m,用曲尺(两直尺相交成直角)从山谷两侧测量出OA=1m,OB=3m,O′A′=0.5m,O′B′=3m(点A,O,O′A′在同一条水平线上),则该山谷的深h为 m.
6.小敏想知道校园内一棵大树的高(如图),她测得CB=10米,∠ACB=50°,请你帮她算出树高AB约为 米.(注:①树垂直于地面;②供选用数据:sin50°≈0.77,cos50°≈0.64,tan50°≈1.2)
7.如图,我校为了筹备校园艺术节,要在通往舞台的台阶上铺上红色地毯.如果地毯的宽度恰好与台阶的宽度一致,台阶的侧面如图所示,台阶的坡角为30°,∠BCA=90°,台阶的高BC为2米,那么请你帮忙算一算需要 米长的地毯恰好能铺好台阶.(结果精确到0.1m,取=1.414,=1.732).
8.为美化小区环境,某小区有一块面积为30m2的等腰三角形草地,测得其一边长为10m,现要给这块三角形草地围上白色的低矮栅栏,则其长度为 m.
9.如图,在一个房间内有一个梯子斜靠在墙上,梯子顶端距地面的垂直距离MA为a米,此时,梯子的倾斜角为75°,如果梯子底端不动,顶端靠在对面墙上N,此时梯子顶端距地面的垂直距离NB为b米,梯子的倾斜角45°,则这间房子的宽AB是 米.
10.如图,青岛位于北纬36°4′,通过计算可以求得:在冬至日正午时分的太阳入射角为30°30′.因此,在规划建设楼高为20米的小区时,两楼间的距离最小为 米,才能保证不挡光(结果保留四个有效数字)(提示:sin30°30′=0.5075,tan30°30′=0.5890).
11.如图梯子AB靠在墙上,梯子的底端A到墙根C的距离为2米,梯子的顶端B到地面的距离为7米,现将梯子的底端A向外移动到A′,使梯子的底端A′到墙根C的距离等于3米,同时梯子的顶端B下降至B′,那么BB′①等于1米②大于1米③小于1米.其中正确结论序号是 .
12.如图,一束光线从y轴上点A(0,1)出发,经过x轴上点C反射后经过点B(3,3),则光线从A点到B点经过的路线长是 .
三.解答题(共10小题,满分68分)
13.如图1、2,图1是一个小朋友玩“滚铁环”的游戏,铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图2.已知铁环的半径为5个单位(每个单位为5cm),设铁环中心为O,铁环钩与铁环相切点为M,铁环与地面接触点为A,∠MOA=α,且sinα=.
(1)求点M离地面AC的高度BM(单位:厘米);
(2)设人站立点C与点A的水平距离AC等于11个单位,求铁环钩MF的长度(单位:厘米).
14.如图所示,某超市在一楼至二楼之间安装有电梯,天花板与地面平行,请你根据图中数据计算回答:小敏身高1.78米,她乘电梯会有碰头危险吗?姚明身高2.29米,他乘电梯会有碰头危险吗?
(可能用到的参考数值:sin27°=0.45,cos27°=0.89,tan27°=0.51)
15.去年夏季山洪暴发,几所学校被山体滑坡推倒教学楼,为防止滑坡,经过地质人员勘测,当坡角不超过45°时,可以确保山体不滑坡.某小学紧挨一座山坡,如图所示,已知AF∥BC,斜坡AB长30米,坡角∠ABC=60°.改造后斜坡BE与地面成45°角,求AE至少是多少米?(精确到0.1米)
16.太阳光线与水平线的夹角在新疆地区的变化较大,夏至时夹角最大,冬至时夹角最小,最小夹角约为28度.现有两幢居民住宅楼高为15米,两楼相距20米,如图所示.
(1)在冬至时,甲楼的影子在乙楼上有多高?
(2)若在本小区内继续兴建同样高的住宅楼,楼距至少应该多少米,才不影响楼房的采光?(前一幢楼房的影子不能落在后一幢楼房上)(计算结果精确到0.1米)
17.某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶.已知看台高为1.6米,现要做一个不锈钢的扶手AB及两根与FG垂直且长为l米的不锈钢架杆AD和BC(杆子的底端分别为D,C),且∠DAB=66.5°.
(1)求点D与点C的高度差DH;
(2)求所用不锈钢材料的总长度l.(即AD+AB+BC,结果精确到0.1米)
(参考数据:sin66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30)
18.如图所示,A、B为两个村庄,AB、BC、CD为公路,BD为田地,AD为河流,且CD与AD互相垂直.现在要从E处开始铺设通往村庄A、村庄B的一条电缆,共有如下两种铺设方案:
方案一:E D A B;
方案二:E C B A.
经测量得AB=4千米,BC=10千米,CE=6千米,∠BDC=45°,∠ABD=15度.已知:地下电缆的修建费为2万元/千米,水下电缆的修建费为4万元/千米.
(1)求出河宽AD(结果保留根号);
(2)求出公路CD的长;
(3)哪种方案铺设电缆的费用低?请说明你的理由.
19.如图是一座人行天桥的示意图,天桥的高是10米,坡面的倾斜角为45°.为了方便行人推车过天桥,市政部门决定降低坡度,使新坡面的倾斜角为30°,若新坡角下需留3米的人行道,问离原坡角10米的建筑物是否需要拆除?(参考数据:≈1.414,≈1.732.)
20.已知:如图,A、B、C三个村庄在一条东西走向的公路沿线上,AB=2km.在B村的正北方向有一个D村,测得∠DAB=45°,∠DCB=28°.今将△ACD区域进行规划,除其中面积为0.5km2的水塘外,准备把剩余的一半作为绿化用地,试求绿化用地的面积.(结果精确到0.1km2,sin28°=0.4695,cos28°=0.8829,tan28°=0.5317,cot28°=1.88.8)
21.如图,在一次龙卷风中,一棵大树在离地面若干千米处折断倒下,B为折断处最高点,树顶A落在离树根C的12米处,测得∠BAC=48°,求BC的长.(借助计算器,精确到0.1米)
22.苏州的虎丘塔塔身倾斜,却历经千年而不倒,被誉为“中国第一斜塔”.如图,BC是过塔底中心B的铅垂线.AC是塔顶A偏离BC的距离.据测量,约为2.34米,倾角约为2°48′,求虎丘塔塔身AB的长度.(精确到0.1米)
参考答案
一.选择题(共4小题,满分20分)
1.解:过D作DF⊥CD,交AE于点F,过F作FG⊥AB,垂足为G.
由题意得:.
∴DF=DE×1.6÷2=14.4(m).
∴GF=BD=CD=6m.
又∵.
∴AG=1.6×6=9.6(m).
∴AB=14.4+9.6=24(m).
答:铁塔的高度为24m.
故选:A.
2.解:∵四边形ABCD为矩形,
∴△ADB为直角三角形,
又∵AD=10,AB=10,
∴BD==20,
又∵cos∠ADB==,
∴∠ADB=60°.
又矩形对角线互相平分且相等,便道的宽为1m,
所以每个扇环都是圆心角为30°,且外环半径为10.5,内环半径为9.5.
∴每个扇环的面积为=.
∴当π取3.14时整条便道面积为=10.4666≈10.5m2.
便道面积约为10.5m2.
故选:C.
3.解:因为AC、BD、法线均和镜面垂直,
所以∠A=∠B=α,
而由已知得△ACE∽△BDE,
所以=即=
∴,
在三角形ACE中tanA====tanα.
故选:D.
4.解:过N点作MA垂线,垂足点D,连接NM.
设梯子底端为C点,AB=x,且AB=ND=x.
∴△BNC为等腰直角三角形,
∴180°﹣45°﹣75°=60°
∴△CNM为等边三角形,梯子长度相同
∵∠NCB=45°,
∴∠DNC=45°,
∴∠MND=60°﹣45°=15°,
∴cos15°=,
又∵∠MCA=75°,
∴∠AMC=15°,
∴cos15°=,
故可得:=.
∵△CNM为等边三角形,
∴NM=CM.
∴x=MA=a.
故选:D.
二.填空题(共8小题,满分32分)
5.解:设A、A′到谷底的水平距离为AC=m,A′C=n.
∴m+n=15.
根据题意知,OB∥CD∥O′B′.
∵OA=1,OB=3,O′A′=0.5,O′B′=3.
∴==3,==6.
∴(+)×h=15.
解得h=30(m).
6.解:由题可知,在Rt△ABC中,tan50°=AB:BC,
∴AB=tan50°×BC≈1.2×10=12(米).
7.解:在Rt△ABC中,∠A=30°,BC=2,∠C=90°.
∵tanA=,∴=2.
∴AC+BC=2+2≈2×1.73+2=5.46≈5.5(m).
即地毯的长度至少需5.5m.
8.解:(1)如图1,当底边BC=10m时,
由于S=30m2,所以高AD=6m,
此时AB=AC==(m),
所以周长=(2+10)m;
(2)①当△ABC是锐角三角形时,如图2,当AB=AC=10m时,高CE=6,此时AE=8m,BE=2m,在Rt△BEC中,BC=2m,
此时周长=(20+2)m.
②当△ABC是钝角三角形时,如图3,设BD=xm,AD=hm,
则在Rt△ABD中,×2x×h=30,
xh=30,
,解得或(舍去),
故△ABC是钝角三角形时,△ABC的周长=2×10+3=(20+6)(m),
故填空答案:2+10或20+2或20+6.
9.解:过N点作MA垂线,垂足点D,连接NM.
由题意得AB=ND,△CNM为等边三角形(180﹣45﹣75=60°,梯子长度相同),
∵∠ACM=75°,
∴∠AMC=15°.
∴∠AMN=75°,
在△MND中,ND=MN×sin75°,
在△MAC中,AM=MC×sin75°,
∵MN=MC,
∴ND=MA=a.
故答案为a.
10.解:由题意可知,光线,楼和地面构成一个直角三角形.
∴tan30°30′=,
所以楼间距=,
即楼间距=≈33.96(米).
11.解:由勾股定理得:梯子AB=,CB′=.
∴BB′=7﹣<1,故选③.
12.解:A关于x轴的对称点A′坐标是(0,﹣1)连接A′B,交x轴于点C,
作DB∥A′A,A′D∥OC,交DB于D,
故光线从点A到点B所经过的路程A′B===5.
三.解答题(共10小题,满分68分)
13.解:过M作与AC平行的直线,与OA、FC分别相交于H、N.
(1)在Rt△OHM中,∠OHM=90°,OM=5,
HM=OM×sinα=3,
所以OH=4,
MB=HA=5﹣4=1,
1×5=5cm.
所以铁环钩离地面的高度为5cm;
(2)∵铁环钩与铁环相切,
∴∠MOH+∠OMH=∠OMH+∠FMN=90°,∠FMN=∠MOH=α,
∴=sinα=,
∴FN=FM,
在Rt△FMN中,∠FNM=90°,MN=BC=AC﹣AB=11﹣3=8.
∵FM2=FN2+MN2,
即FM2=(FM)2+82,
解得:FM=10,
10×5=50(cm).
∴铁环钩的长度FM为50cm.
14.解:姚明乘此电梯会有碰头危险.(1分)
理由:由题意可知:AC∥BD,
∴∠CAB=∠ABD=27°.(2分)
过点C作CE⊥AC交AB于点E,(3分)
在Rt△ACE中,tan∠CAE=,(4分)
∴CE=AC tan∠CAE=4×tan27°≈4×0.51=2.04(米)<2.29(米).
∴姚明乘此电梯会有碰头危险.
∵2.04>1.78,
∴小敏乘此电梯不会有碰头危险.
15.解:在Rt△ADB中,AB=30米∠ABC=60°
AD=AB sin∠ABC=30×sin60°=15≈25.98≈26.0(米),
DB=AB cos∠ABC=30×cos60°=15米.
连接BE,过E作EN⊥BC于N
∵AE∥BC∴四边形AEND是矩形NE=AD≈26米
在Rt△ENB中,由已知∠EBN≤45°,
当∠EBN=45°时,BN=EN=26.0米
∴AE=DN=BN﹣BD=26.0﹣15=11米
答:AE至少是11.0米.
16.解:(1)如图所示,
作DE⊥AB,垂足为E,
由题意可知∠ADE=28°,DE=BC=20,
在Rt△ADE中,tan∠ADE=,
AE=DE tan∠ADE=20 tan28°≈10.6,
则DC=EB=AB﹣AE=15﹣10.6=4.4.
即冬至时甲楼的影子在乙楼上约4.4米高.
(2)若要不影响要房间的采光,如图所示在Rt△ABC中,AB=15,∠C=28°,
BC=≈28.2.
答:楼距至少28.2米,才不影响楼房的采光.
17.解:(1)DH=1.6×=1.2(m);
(2)过B作BM⊥AH于M,则四边形BCHM是矩形.
∴MH=BC=1(m),
∴AM=AH﹣MH=1+1.2﹣1=1.2(m).
在Rt△AMB中,∠A=66.5°.
∴AB=(m).
∴l=AD+AB+BC≈1+3.0+1=5.0(m).
答:点D与点C的高度差DH为1.2m;所用不锈钢材料的总长度约为5.0m.
18.解:(1)过点B作BF⊥AD,交DA的延长线于点F.
由题意得:∠BAF=∠ABD+∠ADB=15°+45°=60°,
在Rt△BFA中,BF=ABsin60°=4×=6(千米),
AF=ABcos60°=4×=2(千米).
∵CD⊥AD,∠BDC=45°,
∴∠BDF=45°,
在Rt△BFD中,∵∠BDF=45°,
∴DF=BF=6千米.
∴AD=DF﹣AF=(6﹣2)(千米).
即河宽AD为(6﹣2)千米;
(2)过点B作BG⊥CD于G,易证四边形BFDG是正方形,
∴BG=BF=6千米.
在Rt△BGC中,=8(千米),
∴CD=CG+GD=14千米.
即公路CD的长为14千米;
(3)方案一的铺设电缆费用低.
由(2)得DE=CD﹣CE=8千米.
∴方案一的铺设费用为:2(DE+AB)+4AD=40万元,
方案二的铺设费用为:2(CE+BC+AB)=(32+8)万元.
∵40<32+8,
∴方案一的铺设电缆费用低.
19.解:∵∠CAB=45°.
∴AB=BC=10.
∵∠CDB=30°.
∴BD=10.
∴AD=10﹣10≈7.32.(7分)
∵7.32+3>10.
答:离原坡角10米的建筑物需要拆除.(10分)
20.解:在Rt△ABD中,
∵∠ABD=90°,∠BAD=45°,∠ADB=45°,
∴BD=AB=2km,
在Rt△BCD中,
∵cot∠BCD=,∠DCB=28°,
∴BC=BD cot∠BCD=2cot28°(km),
∴S△ACD=AC BD=(2+2cot28°)(km2).
∴S绿地=(2+2cot28°)≈2.6(km2).
答:绿化用地的面积为2.6km2.
21.解:在直角△ABC中,tan∠BAC=
∴BC=AC tan48°=12tan48°≈13.3米.
22.解:在Rt△ABC中,∵sin∠ABC=
∴
=
≈47.9.
答:虎丘塔塔身AB长约为47.9m.
