2021-2022学年鲁教版(五四制)九年级数学下册5.6直线与圆的位置关系 同步达标测评(word版含答案)
文档属性
| 名称 | 2021-2022学年鲁教版(五四制)九年级数学下册5.6直线与圆的位置关系 同步达标测评(word版含答案) |  | |
| 格式 | doc | ||
| 文件大小 | 643.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 鲁教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-17 22:12:45 | ||
图片预览



文档简介
2021-2022学年鲁教版九年级数学下册《5.6直线与圆的位置关系》同步达标测评(附答案)
一.选择题(共6小题,满分30分)
1.如图,在平面直角坐标系中,已知⊙O的半径为2,动直线AB与x轴交于点P(x,0),直线AB与x轴正方向夹角为45°,若直线AB与⊙O有公共点,则x的取值范围是( )
A.﹣2≤x≤2 B.﹣2<x<2 C.0≤x≤2 D.﹣2≤x≤2
2.如图,在⊙O中,将沿弦AB翻折交半径AO的延长线于点D,延长BD交⊙O于点C,AC切所在的圆于点A,则tan∠C的值是( )
A. B. C.2+ D.1+
3.如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B,点M和点N分别是l1和l2上的动点,MN沿l1和l2平移,若⊙O的半径为1,∠1=60°,下列结论错误的是( )
A.MN= B.若MN与⊙O相切,则AM=
C.l1和l2的距离为2 D.若∠MON=90°,则MN与⊙O相切
4.如图,以OB为直径的半圆与半圆O交于点P,A、O、C、B在同一条直线上,作AD⊥AB与BP的延长线交于点D,若半圆O的半径为2,∠D的余弦值是方程3x2﹣10x+3=0的根,则AB的长等于( )
A. B. C.8 D.5
5.已知△ABC的三边长为AB=2,BC=3,AC=4,则三角形内切圆半径为( )
A. B. C. D.
6.如图,AB是⊙O的直径,CE切⊙O于点C交AB的延长线于点E.设点D是弦AC上任意一点(不含端点),若∠CEA=30°,BE=4,则CD+2OD的最小值为( )
A.2 B. C.4 D.4
二.填空题(共6小题,满分30分)
7.设抛物线y=﹣x2+2x+3的顶点为E,与y轴交于点C,EF⊥x轴于点,若点M(m,0)是x轴上的动点,且满足以MC为直径的圆与线段EF有公共点,则实数m的取值范围是 .
8.如图,矩形ABCD中,AB=4,AD=8,点E,F分别在边AD,BC上,且点B,F关于过点E的直线对称,如果EF与以CD为直径的圆恰好相切,那么AE= .
9.如图,点C在以AB为直径的半圆上,AB=10,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为5;③当AD=3时,EF与半圆相切;④若点F恰好落在弧BC上,则AD=5;⑤当点D从点A运动到B点时,线段EF扫过的面积是20.其中正确结论的序号是 .
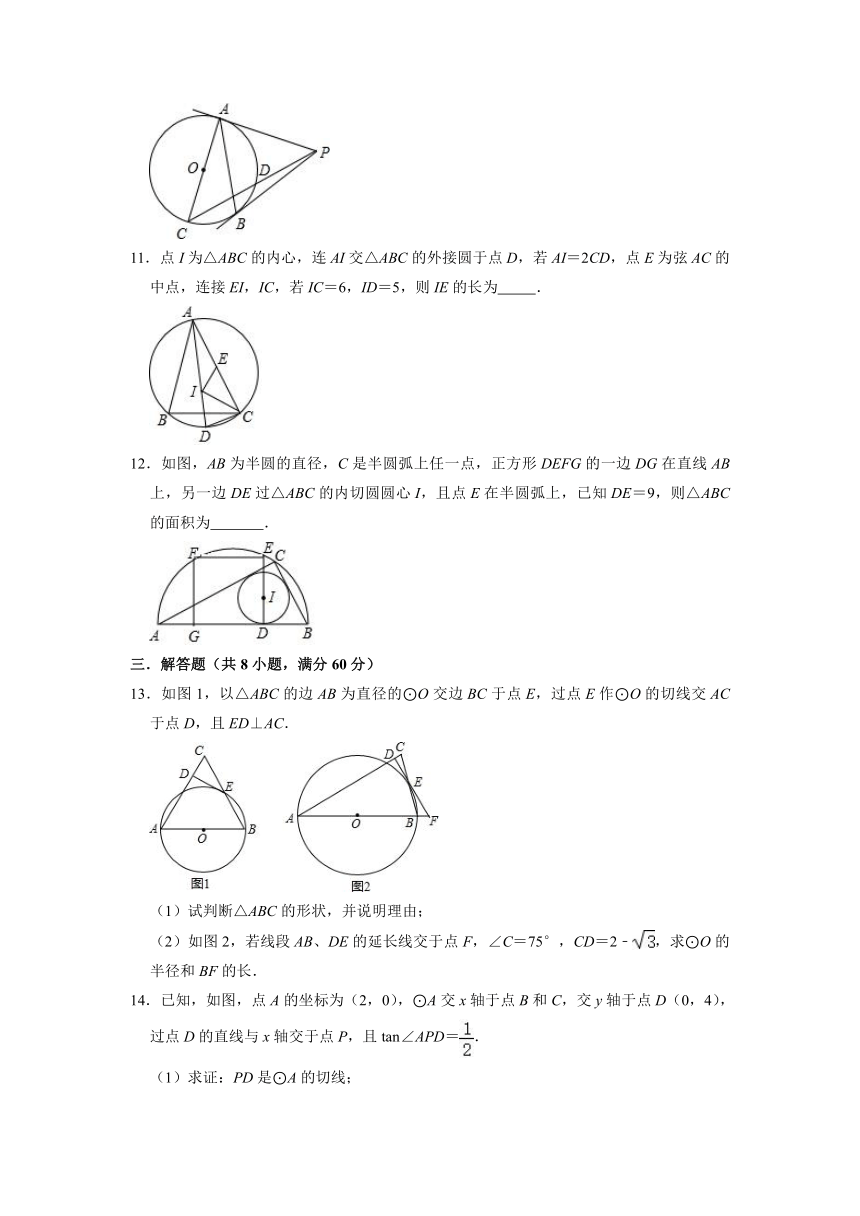
10.如图,PA、PB与⊙O分别相切于点A、点B,AC是⊙O的直径,PC交⊙O于点D,已知∠APB=60°,AC=2,那么CD的长为 .
11.点I为△ABC的内心,连AI交△ABC的外接圆于点D,若AI=2CD,点E为弦AC的中点,连接EI,IC,若IC=6,ID=5,则IE的长为 .
12.如图,AB为半圆的直径,C是半圆弧上任一点,正方形DEFG的一边DG在直线AB上,另一边DE过△ABC的内切圆圆心I,且点E在半圆弧上,已知DE=9,则△ABC的面积为 .
三.解答题(共8小题,满分60分)
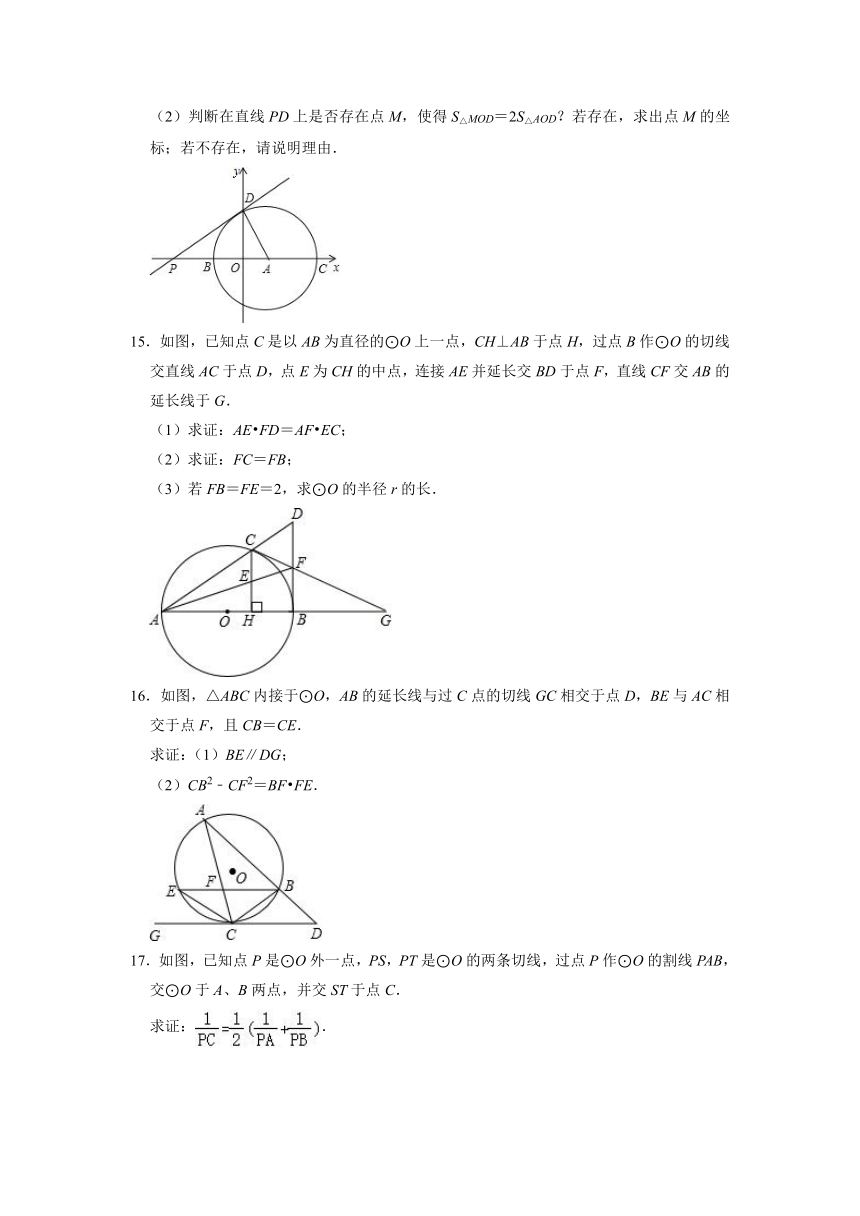
13.如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作⊙O的切线交AC于点D,且ED⊥AC.
(1)试判断△ABC的形状,并说明理由;
(2)如图2,若线段AB、DE的延长线交于点F,∠C=75°,CD=2﹣,求⊙O的半径和BF的长.
14.已知,如图,点A的坐标为(2,0),⊙A交x轴于点B和C,交y轴于点D(0,4),过点D的直线与x轴交于点P,且tan∠APD=.
(1)求证:PD是⊙A的切线;
(2)判断在直线PD上是否存在点M,使得S△MOD=2S△AOD?若存在,求出点M的坐标;若不存在,请说明理由.
15.如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,直线CF交AB的延长线于G.
(1)求证:AE FD=AF EC;
(2)求证:FC=FB;
(3)若FB=FE=2,求⊙O的半径r的长.
16.如图,△ABC内接于⊙O,AB的延长线与过C点的切线GC相交于点D,BE与AC相交于点F,且CB=CE.
求证:(1)BE∥DG;
(2)CB2﹣CF2=BF FE.
17.如图,已知点P是⊙O外一点,PS,PT是⊙O的两条切线,过点P作⊙O的割线PAB,交⊙O于A、B两点,并交ST于点C.
求证:.
18.已知△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F,若=,如图1.
(1)判断△ABC的形状,并证明你的结论;
(2)设AE与DF相交于点M,如图2,AF=2FC=4,求AM的长.
19.如图,已知四边形ABCD是平行四边形,AD与△ABC的外接圆⊙O恰好相切于点A,边CD与⊙O相交于点E,连接AE,BE.
(1)求证:AB=AC;
(2)若过点A作AH⊥BE于H,求证:BH=CE+EH.
20.如图,在△ABC中,∠ABC=∠ACB,AC为直径的⊙O分别交AB、BC于点M,N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线;
(2)若BC=2,sin∠BCP=,求△ACP的周长.
参考答案
一.选择题(共6小题,满分30分)
1.解:如图所示,当AB与⊙O相切时,有一个公共点,设这个公共点为G,连接OG,则OG⊥CD,
这时OG=2,∠OCD=45°,
sin45°=,
OC==2,
即x=2,
如果直线AB在第二象限与圆相切,这时同理可求得x=﹣2,
∴x的取值范围是﹣2≤x≤2,
故选:D.
2.解:作点D关于AB的对称点H,连接AH,BH,CH.
根据对称性可知,所在圆的圆心在直线AH上,
∵AC切所在的圆于点A,
∴AC⊥AH,
∴∠CAH=90°,
∴CH是⊙O的直径,
∴∠CBH=90°,
∴∠ABD=∠ABH=45°,
∴∠AHC=∠ABC=45°,
∴∠ACH=∠AHC=45°,
∴AC=AH,
∵OC=OH,
∴AD垂直平分线段CH,
∴DC=DH,
∴∠DCH=∠DHC,
∵BD=BH,
∴∠BDH=∠BHD=45°,
∵∠BDH=∠DCH+∠DHC,
∴∠DCH=22.5°,
∴∠ACD=∠CHB=67.5°,
设BD=BH=a,则CD=DH=a,
∴tan∠ACB=tan∠CHB===1+,
故选:D.
3.解:连接OA、OB,如图1,
∵⊙O与l1和l2分别相切于点A和点B,
∴OA⊥l1,OB⊥l2,
∵l1∥l2,
∴点A、O、B共线,
∴AB为⊙O的直径,
∴l1和l2的距离为2;故C正确,
作NH⊥AM于H,如图1,
则HN=AB=2,
∵∠AMN=60°,
∴sin60°=,
∴MN=;故A正确,
当MN与⊙O相切,如图2,连接OM,ON,
当MN在AB左侧时,∠AMO=∠AMN=×60°=30°,
在Rt△AMO中,tan∠AMO=,即AM==,
在Rt△OBN中,∠ONB=∠ONM=60°,tan∠ONB=,即BN==,
当MN在AB右侧时,AM=,
∴AM的长为 或;故B错误,
当∠MON=90°时,作OE⊥MN于E,延长NO交l1于F,如图2,
∵OA=OB,
∴Rt△OAF≌Rt△OBN,
∴OF=ON,
∴MO垂直平分NF,
∴OM平分∠NMF,
∴OE=OA,
∴MN为⊙O的切线.故D正确.
故选:B.
4.解:∵3x2﹣10x+3=0,
∴x=3(不合题意,舍去)或x=.
∴cosD=AD:BD=1:3,
设AD=x,则BD=3x.
∴AB==2x,BC=2x﹣4.
∴(2x)2=(2x﹣4) x.
∴x=0(舍去),或x=2.
∴AB=2×2=8.
故选:C.
5.解:过点C作CD⊥AB,垂足为D,连接AI,BI,CI,设△ABC内切圆的半径为r,
设AD=x,则BD=2﹣x,
由勾股定理得:CD2=AC2﹣AD2,CD2=BC2﹣BD2.
∴42﹣x2=32﹣(2﹣x)2.
解得:x=2.75.
∴CD===,
∴S△ABC=S△AOC+S△ABO+S△BCO,
∴=+,
∴=×4×r,
解得:r=,
故选:B.
6.解:如图,作OF平分∠AOC,交⊙O于F,连接AF、CF、DF,
∵CE切⊙O于点C,
∴∠OCE=90°,
又∵∠CEA=30°,
∴∠AOC=120°,
则∠AOF=∠COF=∠AOC=(180°﹣60°)=60°.
∵BE=4,
∴2OC=OB+BE,即2OC=OC+4,
则OC=4,即圆的半径为4,
∵OA=OF=OC,
∴△AOF、△COF是等边三角形,
∴AF=AO=OC=FC,
∴四边形AOCF是菱形,
∴根据对称性可得DF=DO.
过点D作DH⊥OC于H,
∵OA=OC,∴∠OCA=∠OAC=30°,
∴DH=DC sin∠DCH=DC sin30°=DC,
∴CD+OD=DH+FD.
根据垂线段最短可得:
当F、D、H三点共线时,DH+FD(即CD+OD)最小,此时CD+2OD=2(DH+FD),
∵FH=OF sin∠FOH=OF=2,
∴CD+2OD=2(DH+FD)=2FH=4,
故选:D.
二.填空题(共6小题,满分30分)
7.解:∵M(m,0),C(0,3),
∴圆心N的坐标(,),
圆N的半径为:,
圆心到EF的距离为:|1﹣|,
由题意得,
|1﹣|≤≤,
解得:﹣≤m≤5.
故答案为:﹣≤m≤5.
8.解:如图,设⊙O与EF相切于M,连接EB,作EH⊥BC于H.
由题意易知四边形AEHB是矩形,设AE=BH=x,
由切线长定理可知,ED=EM,FC=FM,
∵B、F关于EH对称,
∴HF=BH=x,ED=EM=8﹣x,FC=FM=8﹣2x,EF=16﹣3x,
在Rt△EFH中,∵EF2=EH2+HF2,
∴42+x2=(16﹣3x)2,
解得x=6﹣或6+(舍弃),
∴AE=6﹣,
故答案为:6﹣.
9.解:①连接CD,如图1所示.
∵点E与点D关于AC对称,
∴CE=CD.
∴∠E=∠CDE.
∵DF⊥DE,
∴∠EDF=90°.
∴∠E+∠F=90°,∠CDE+∠CDF=90°.
∴∠F=∠CDF.
∴CD=CF.
∴CE=CD=CF.
∴结论“CE=CF”正确.
②当CD⊥AB时,如图2所示.
∵AB是半圆的直径,
∴∠ACB=90°.
∵AB=10,∠CBA=30°,
∴∠CAB=60°,AC=5,BC=5.
∵CD⊥AB,∠CBA=30°,
∴CD=BC=.
根据“点到直线之间,垂线段最短”可得:
点D在线段AB上运动时,CD的最小值为.
∵CE=CD=CF,
∴EF=2CD.
∴线段EF的最小值为5.
∴结论“线段EF的最小值为5”正确.
③当AD=3时,连接OC,如图3所示.
∵OA=OC,∠CAB=60°,
∴△OAC是等边三角形.
∴CA=CO,∠ACO=60°.
∵AO=5,AD=3,
∴DO=2.
∴AD≠DO.
∴∠ACD>∠OCD≠30°.
∵点E与点D关于AC对称,
∴∠ECA=∠DCA.
∴∠ECA≠30°.
∴∠ECO≠90°.
∴OC不垂直EF.
∵EF经过半径OC的外端,且OC不垂直EF,
∴EF与半圆不相切.
∴结论“EF与半圆相切”错误.
④当点F恰好落在上时,连接FB、AF,如图4所示.
∵点E与点D关于AC对称,
∴ED⊥AC.
∴∠AGD=90°.
∴∠AGD=∠ACB.
∴ED∥BC.
∴△FHC∽△FDE.
∴=.
∵FC=EF,
∴FH=FD.
∴FH=DH.
∵DE∥BC,
∴∠FHC=∠FDE=90°.
∴BF=BD.
∴∠FBH=∠DBH=30°.
∴∠FBD=60°.
∵AB是半圆的直径,
∴∠AFB=90°.
∴∠FAB=30°.
∴FB=AB=5.
∴DB=4.
∴AD=AB﹣DB=5.
∴结论“AD=5”正确.
⑤∵点D与点E关于AC对称,
点D与点F关于BC对称,
∴当点D从点A运动到点B时,
点E的运动路径AM与AB关于AC对称,
点F的运动路径NB与AB关于BC对称.
∴EF扫过的图形就是图5中阴影部分.
∴S阴影=2S△ABC
=2×AC BC
=AC BC
=5×5=25.
∴EF扫过的面积为25.
∴结论“EF扫过的面积为20”错误.
故答案为:①、②、④.
10.解:连接AD,OB,OP;
∵PA、PB与⊙O分别相切于点A、点B,
∴∠OAP=∠OBP=90°,∠AOB=180°﹣∠P=120°,
∴∠AOP=60°,AP=AOtan60°=,
∴PC=;
∵PA2=PD PC,
∴PD=,
∴CD=.
11.解:延长ID到M,使得DM=ID,连接CM.
∵I是△ABC的内心,
∴∠IAC=∠IAB,∠ICA=∠ICB,
∵∠DIC=∠IAC+∠ICA,∠DCI=∠BCD+∠ICB,∠BCD=∠IAB,
∴∠DIC=∠DCI,
∴DI=DC=DM,
∴∠ICM=90°,
∴CM==8,
∵AI=2CD=10,
∴AI=IM,∵AE=EC,
∴IE=CM=4,
故答案为4.
12.解:设⊙I切AC与M,切BC于N,半径为r,
则AD=AM,CM=CN=r,BD=BN,r=(AC+BC﹣AB),
∵AB为半圆的直径,
∴∠ACB=90°,
∴AB2=AC2+BC2,
∴AD DB=AM BN=(AC﹣r)(BC﹣r)=[AC﹣(AC+BC﹣AB)][BC﹣(AC+BC﹣AB)]
=(AC﹣BC+AB)(AB+BC﹣AC)=(AB2﹣AC2﹣BC2+2AC BC)=AC BC,
由射影定理得AD DB=DE2=81,
∴S△ABC=AC BC=81,
故答案为:81.
三.解答题(共8小题,满分60分)
13.解:(1)△ABC是等腰三角形,理由是:
如图1,连接OE,
∵DE是⊙O的切线,
∴OE⊥DE,
∵ED⊥AC,
∴AC∥OE,
∴∠1=∠C,
∵OB=OE,
∴∠1=∠B,
∴∠B=∠C,
∴△ABC是等腰三角形;
(2)如图2,过点O作OG⊥AC,垂足为G,则得四边形OGDE是矩形,
∵△ABC是等腰三角形,
∴∠B=∠C=75°,
∴∠A=180°﹣75°﹣75°=30°,
设OG=x,则OA=OB=OE=2x,AG=x,
∴DG=OE=2x,
根据AC=AB得:4x=x+2x+2﹣,
x=1,
∴OE=OB=2,
在直角△OEF中,∠EOF=∠A=30°,
cos30=,OF==2÷=,
∴BF=﹣2,⊙O的半径为2.
14.(1)证明:∵A(2,0)D(0,4),
∴AO=2,OD=4,
∴在Rt△ADO中,tan∠ADO===,
∵tan∠APD=,
∴∠ADO=∠APD,
∵∠AOD=90°,
∴∠ADO+∠DAO=90°,
∴∠DAO+∠APD=90°,
∴∠PDA=180°﹣90°=90°,
∴AD⊥PD,
∵AD是⊙A的半径,
∴PD是⊙A的切线.
(2)解:在△ADO中,OA=2,OD=4,由勾股定理得:AD=2,
在Rt△PDA中,tan∠APD==,
即PD=4,
由勾股定理得:AP==10,
∵OA=2,
∴OP=8,
即P(﹣8,0),
∵D(0,4),
∴设直线PD的解析式是:y=kx+4,
把P的坐标代入得:0=﹣8k+4,
解得:k=,
∴直线PD的解析式是y=x+4,
假如存在M点,使得S△MOD=2S△AOD,
设M的坐标是(x,x+4),
如图:
当M在y轴的左边时,过M作MN⊥OD于N,
∵S△MOD=2S△AOD,
∴×4×(﹣x)=2××2×4,
解得:x=﹣4,
y=x+4=2,
即此时M坐标是(﹣4,2),
当M点在y轴的右边时,同法可求M的横坐标是4,代入y=x+4得y=6,
此时M的坐标是(4,6),
即在直线PD上存在点M,使得S△MOD=2S△AOD,点M的坐标是(﹣4,2)或(4,6).
15.(1)证明:∵BD是⊙O的切线,
∴∠DBA=90°,
∵CH⊥AB,
∴CH∥BD,
∴△AEC∽△AFD,
∴=,
∴AE FD=AF EC.
(2)证明:连接OC,BC,
∵CH∥BD,
∴△AEC∽△AFD,△AHE∽△ABF,
∴=,=,
∴==,
∵CE=EH(E为CH中点),
∴BF=DF,
∵AB为⊙O的直径,
∴∠ACB=∠DCB=90°,
∵BF=DF,
∴CF=DF=BF(直角三角形斜边上的中线等于斜边的一半),
即CF=BF.
(3)解:连接OF,
∵FE=FB=2,
∴FC=FE=2,
∴∠FEC=∠FCE,
∵∠FCE+∠G=∠FEC+∠FAB=90°,
∴∠FAB=∠G,
∴FA=FG,
∴AB=BG,
∵AO=OB,BF=DF,
∴OF∥AC,
∴==3,
∴FG=3FC=6,
∴由勾股定理得:BG===4,
∴OA=OB=AB=BG=2,
即⊙O的半径r的长为2.
16.证明:(1)∵CB=CE,
∴∠E=∠CBE.
∵CG为⊙O切线,
∴∠BCD=∠E.
∴∠CBE=∠BCD.
∴BE∥DG.
(2)∵∠A=∠E,
∴∠A=∠CBE.
∵∠ACB=∠ACB,
∴△CBF∽△CAB,.
∴CB2=CF AC=CF (CF+AF)=CF2+CF AF.
即CB2﹣CF2=AF CF.
由相交弦定理,得AF CF=BF FE.
∴CB2﹣CF2=BF FE.
17.证明:连PO交ST于点D,则PO⊥ST;
连SO,作OE⊥PB于E,则E为AB中点,
于是
因为C、E、O、D四点共圆,
所以PC PE=PD PO
又因为Rt△SPD∽Rt△OPS
所以
即PS2=PD PO
而由切割线定理知PS2=PA PB
所以
即
18.解:(1)连接OA.结论:△ABC为等腰三角形,
理由:∵=,
∴∠EOF=∠DOE,
又∵∠EOF+∠C=180°,∠DOE+∠B=180°,
∴∠C=∠B,
∴AB=AC,
∴△ABC为等腰三角形;
(2)连接OB、OC、OD、OF,如图,
∵等腰三角形ABC中,AE⊥BC,
∴E是BC中点,BE=CE,
在Rt△AOF和Rt△AOD中,
,
∴Rt△AOF≌Rt△AOD,
∴AF=AD,
同理Rt△COF≌Rt△COE,CF=CE=2,
Rt△BOD≌Rt△BOE,BD=BE,
∴AD=AF,BD=CF,
∴DF∥BC,
∴=,
∵AE==4,
∴AM=4×=.
19.证明:(1)∵AD与△ABC的外接圆⊙O恰好相切于点A,
∴∠ABE=∠DAE,又∠EAC=∠EBC,
∴∠DAC=∠ABC,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠ABC=∠ACB,
∴AB=AC;
(2)作AF⊥CD于F,
∵四边形ABCE是圆内接四边形,
∴∠ABC=∠AEF,又∠ABC=∠ACB,
∴∠AEF=∠ACB,又∠AEB=∠ACB,
∴∠AEH=∠AEF,
在△AEH和△AEF中,
,
∴△AEH≌△AEF,
∴EH=EF,
∴CE+EH=CF,
在△ABH和△ACF中,
,
∴△ABH≌△ACF,
∴BH=CF=CE+EH.
20.(1)证明:连接AN,
∵∠ABC=∠ACB,
∴AB=AC,
∵AC是⊙O的直径,
∴AN⊥BC,
∴∠CAN=∠BAN,BN=CN,
∵∠CAB=2∠BCP,
∴∠CAN=∠BCP.
∵∠CAN+∠ACN=90°,
∴∠BCP+∠ACN=90°,
∴CP⊥AC
∵OC是⊙O的半径
∴CP是⊙O的切线;
(2)解:∵∠ANC=90°,sin∠BCP=,
∴=,
∴AC=5,
∴⊙O的半径为
如图,过点B作BD⊥AC于点D.
由(1)得BN=CN=BC=,
在Rt△CAN中,AN==2,
在△CAN和△CBD中,
∠ANC=∠BDC=90°,∠ACN=∠BCD,
∴△CAN∽△CBD,
∴=,
∴BD=4.
在Rt△BCD中,CD==2,
∴AD=AC﹣CD=5﹣2=3,
∵BD∥CP,
∴=,=
∴CP=,BP=
∴△APC的周长是AC+PC+AP=20.
一.选择题(共6小题,满分30分)
1.如图,在平面直角坐标系中,已知⊙O的半径为2,动直线AB与x轴交于点P(x,0),直线AB与x轴正方向夹角为45°,若直线AB与⊙O有公共点,则x的取值范围是( )
A.﹣2≤x≤2 B.﹣2<x<2 C.0≤x≤2 D.﹣2≤x≤2
2.如图,在⊙O中,将沿弦AB翻折交半径AO的延长线于点D,延长BD交⊙O于点C,AC切所在的圆于点A,则tan∠C的值是( )
A. B. C.2+ D.1+
3.如图,直线l1∥l2,⊙O与l1和l2分别相切于点A和点B,点M和点N分别是l1和l2上的动点,MN沿l1和l2平移,若⊙O的半径为1,∠1=60°,下列结论错误的是( )
A.MN= B.若MN与⊙O相切,则AM=
C.l1和l2的距离为2 D.若∠MON=90°,则MN与⊙O相切
4.如图,以OB为直径的半圆与半圆O交于点P,A、O、C、B在同一条直线上,作AD⊥AB与BP的延长线交于点D,若半圆O的半径为2,∠D的余弦值是方程3x2﹣10x+3=0的根,则AB的长等于( )
A. B. C.8 D.5
5.已知△ABC的三边长为AB=2,BC=3,AC=4,则三角形内切圆半径为( )
A. B. C. D.
6.如图,AB是⊙O的直径,CE切⊙O于点C交AB的延长线于点E.设点D是弦AC上任意一点(不含端点),若∠CEA=30°,BE=4,则CD+2OD的最小值为( )
A.2 B. C.4 D.4
二.填空题(共6小题,满分30分)
7.设抛物线y=﹣x2+2x+3的顶点为E,与y轴交于点C,EF⊥x轴于点,若点M(m,0)是x轴上的动点,且满足以MC为直径的圆与线段EF有公共点,则实数m的取值范围是 .
8.如图,矩形ABCD中,AB=4,AD=8,点E,F分别在边AD,BC上,且点B,F关于过点E的直线对称,如果EF与以CD为直径的圆恰好相切,那么AE= .
9.如图,点C在以AB为直径的半圆上,AB=10,∠CBA=30°,点D在线段AB上运动,点E与点D关于AC对称,DF⊥DE于点D,并交EC的延长线于点F.下列结论:①CE=CF;②线段EF的最小值为5;③当AD=3时,EF与半圆相切;④若点F恰好落在弧BC上,则AD=5;⑤当点D从点A运动到B点时,线段EF扫过的面积是20.其中正确结论的序号是 .
10.如图,PA、PB与⊙O分别相切于点A、点B,AC是⊙O的直径,PC交⊙O于点D,已知∠APB=60°,AC=2,那么CD的长为 .
11.点I为△ABC的内心,连AI交△ABC的外接圆于点D,若AI=2CD,点E为弦AC的中点,连接EI,IC,若IC=6,ID=5,则IE的长为 .
12.如图,AB为半圆的直径,C是半圆弧上任一点,正方形DEFG的一边DG在直线AB上,另一边DE过△ABC的内切圆圆心I,且点E在半圆弧上,已知DE=9,则△ABC的面积为 .
三.解答题(共8小题,满分60分)
13.如图1,以△ABC的边AB为直径的⊙O交边BC于点E,过点E作⊙O的切线交AC于点D,且ED⊥AC.
(1)试判断△ABC的形状,并说明理由;
(2)如图2,若线段AB、DE的延长线交于点F,∠C=75°,CD=2﹣,求⊙O的半径和BF的长.
14.已知,如图,点A的坐标为(2,0),⊙A交x轴于点B和C,交y轴于点D(0,4),过点D的直线与x轴交于点P,且tan∠APD=.
(1)求证:PD是⊙A的切线;
(2)判断在直线PD上是否存在点M,使得S△MOD=2S△AOD?若存在,求出点M的坐标;若不存在,请说明理由.
15.如图,已知点C是以AB为直径的⊙O上一点,CH⊥AB于点H,过点B作⊙O的切线交直线AC于点D,点E为CH的中点,连接AE并延长交BD于点F,直线CF交AB的延长线于G.
(1)求证:AE FD=AF EC;
(2)求证:FC=FB;
(3)若FB=FE=2,求⊙O的半径r的长.
16.如图,△ABC内接于⊙O,AB的延长线与过C点的切线GC相交于点D,BE与AC相交于点F,且CB=CE.
求证:(1)BE∥DG;
(2)CB2﹣CF2=BF FE.
17.如图,已知点P是⊙O外一点,PS,PT是⊙O的两条切线,过点P作⊙O的割线PAB,交⊙O于A、B两点,并交ST于点C.
求证:.
18.已知△ABC的内切圆⊙O与AB、BC、AC分别相切于点D、E、F,若=,如图1.
(1)判断△ABC的形状,并证明你的结论;
(2)设AE与DF相交于点M,如图2,AF=2FC=4,求AM的长.
19.如图,已知四边形ABCD是平行四边形,AD与△ABC的外接圆⊙O恰好相切于点A,边CD与⊙O相交于点E,连接AE,BE.
(1)求证:AB=AC;
(2)若过点A作AH⊥BE于H,求证:BH=CE+EH.
20.如图,在△ABC中,∠ABC=∠ACB,AC为直径的⊙O分别交AB、BC于点M,N,点P在AB的延长线上,且∠CAB=2∠BCP.
(1)求证:直线CP是⊙O的切线;
(2)若BC=2,sin∠BCP=,求△ACP的周长.
参考答案
一.选择题(共6小题,满分30分)
1.解:如图所示,当AB与⊙O相切时,有一个公共点,设这个公共点为G,连接OG,则OG⊥CD,
这时OG=2,∠OCD=45°,
sin45°=,
OC==2,
即x=2,
如果直线AB在第二象限与圆相切,这时同理可求得x=﹣2,
∴x的取值范围是﹣2≤x≤2,
故选:D.
2.解:作点D关于AB的对称点H,连接AH,BH,CH.
根据对称性可知,所在圆的圆心在直线AH上,
∵AC切所在的圆于点A,
∴AC⊥AH,
∴∠CAH=90°,
∴CH是⊙O的直径,
∴∠CBH=90°,
∴∠ABD=∠ABH=45°,
∴∠AHC=∠ABC=45°,
∴∠ACH=∠AHC=45°,
∴AC=AH,
∵OC=OH,
∴AD垂直平分线段CH,
∴DC=DH,
∴∠DCH=∠DHC,
∵BD=BH,
∴∠BDH=∠BHD=45°,
∵∠BDH=∠DCH+∠DHC,
∴∠DCH=22.5°,
∴∠ACD=∠CHB=67.5°,
设BD=BH=a,则CD=DH=a,
∴tan∠ACB=tan∠CHB===1+,
故选:D.
3.解:连接OA、OB,如图1,
∵⊙O与l1和l2分别相切于点A和点B,
∴OA⊥l1,OB⊥l2,
∵l1∥l2,
∴点A、O、B共线,
∴AB为⊙O的直径,
∴l1和l2的距离为2;故C正确,
作NH⊥AM于H,如图1,
则HN=AB=2,
∵∠AMN=60°,
∴sin60°=,
∴MN=;故A正确,
当MN与⊙O相切,如图2,连接OM,ON,
当MN在AB左侧时,∠AMO=∠AMN=×60°=30°,
在Rt△AMO中,tan∠AMO=,即AM==,
在Rt△OBN中,∠ONB=∠ONM=60°,tan∠ONB=,即BN==,
当MN在AB右侧时,AM=,
∴AM的长为 或;故B错误,
当∠MON=90°时,作OE⊥MN于E,延长NO交l1于F,如图2,
∵OA=OB,
∴Rt△OAF≌Rt△OBN,
∴OF=ON,
∴MO垂直平分NF,
∴OM平分∠NMF,
∴OE=OA,
∴MN为⊙O的切线.故D正确.
故选:B.
4.解:∵3x2﹣10x+3=0,
∴x=3(不合题意,舍去)或x=.
∴cosD=AD:BD=1:3,
设AD=x,则BD=3x.
∴AB==2x,BC=2x﹣4.
∴(2x)2=(2x﹣4) x.
∴x=0(舍去),或x=2.
∴AB=2×2=8.
故选:C.
5.解:过点C作CD⊥AB,垂足为D,连接AI,BI,CI,设△ABC内切圆的半径为r,
设AD=x,则BD=2﹣x,
由勾股定理得:CD2=AC2﹣AD2,CD2=BC2﹣BD2.
∴42﹣x2=32﹣(2﹣x)2.
解得:x=2.75.
∴CD===,
∴S△ABC=S△AOC+S△ABO+S△BCO,
∴=+,
∴=×4×r,
解得:r=,
故选:B.
6.解:如图,作OF平分∠AOC,交⊙O于F,连接AF、CF、DF,
∵CE切⊙O于点C,
∴∠OCE=90°,
又∵∠CEA=30°,
∴∠AOC=120°,
则∠AOF=∠COF=∠AOC=(180°﹣60°)=60°.
∵BE=4,
∴2OC=OB+BE,即2OC=OC+4,
则OC=4,即圆的半径为4,
∵OA=OF=OC,
∴△AOF、△COF是等边三角形,
∴AF=AO=OC=FC,
∴四边形AOCF是菱形,
∴根据对称性可得DF=DO.
过点D作DH⊥OC于H,
∵OA=OC,∴∠OCA=∠OAC=30°,
∴DH=DC sin∠DCH=DC sin30°=DC,
∴CD+OD=DH+FD.
根据垂线段最短可得:
当F、D、H三点共线时,DH+FD(即CD+OD)最小,此时CD+2OD=2(DH+FD),
∵FH=OF sin∠FOH=OF=2,
∴CD+2OD=2(DH+FD)=2FH=4,
故选:D.
二.填空题(共6小题,满分30分)
7.解:∵M(m,0),C(0,3),
∴圆心N的坐标(,),
圆N的半径为:,
圆心到EF的距离为:|1﹣|,
由题意得,
|1﹣|≤≤,
解得:﹣≤m≤5.
故答案为:﹣≤m≤5.
8.解:如图,设⊙O与EF相切于M,连接EB,作EH⊥BC于H.
由题意易知四边形AEHB是矩形,设AE=BH=x,
由切线长定理可知,ED=EM,FC=FM,
∵B、F关于EH对称,
∴HF=BH=x,ED=EM=8﹣x,FC=FM=8﹣2x,EF=16﹣3x,
在Rt△EFH中,∵EF2=EH2+HF2,
∴42+x2=(16﹣3x)2,
解得x=6﹣或6+(舍弃),
∴AE=6﹣,
故答案为:6﹣.
9.解:①连接CD,如图1所示.
∵点E与点D关于AC对称,
∴CE=CD.
∴∠E=∠CDE.
∵DF⊥DE,
∴∠EDF=90°.
∴∠E+∠F=90°,∠CDE+∠CDF=90°.
∴∠F=∠CDF.
∴CD=CF.
∴CE=CD=CF.
∴结论“CE=CF”正确.
②当CD⊥AB时,如图2所示.
∵AB是半圆的直径,
∴∠ACB=90°.
∵AB=10,∠CBA=30°,
∴∠CAB=60°,AC=5,BC=5.
∵CD⊥AB,∠CBA=30°,
∴CD=BC=.
根据“点到直线之间,垂线段最短”可得:
点D在线段AB上运动时,CD的最小值为.
∵CE=CD=CF,
∴EF=2CD.
∴线段EF的最小值为5.
∴结论“线段EF的最小值为5”正确.
③当AD=3时,连接OC,如图3所示.
∵OA=OC,∠CAB=60°,
∴△OAC是等边三角形.
∴CA=CO,∠ACO=60°.
∵AO=5,AD=3,
∴DO=2.
∴AD≠DO.
∴∠ACD>∠OCD≠30°.
∵点E与点D关于AC对称,
∴∠ECA=∠DCA.
∴∠ECA≠30°.
∴∠ECO≠90°.
∴OC不垂直EF.
∵EF经过半径OC的外端,且OC不垂直EF,
∴EF与半圆不相切.
∴结论“EF与半圆相切”错误.
④当点F恰好落在上时,连接FB、AF,如图4所示.
∵点E与点D关于AC对称,
∴ED⊥AC.
∴∠AGD=90°.
∴∠AGD=∠ACB.
∴ED∥BC.
∴△FHC∽△FDE.
∴=.
∵FC=EF,
∴FH=FD.
∴FH=DH.
∵DE∥BC,
∴∠FHC=∠FDE=90°.
∴BF=BD.
∴∠FBH=∠DBH=30°.
∴∠FBD=60°.
∵AB是半圆的直径,
∴∠AFB=90°.
∴∠FAB=30°.
∴FB=AB=5.
∴DB=4.
∴AD=AB﹣DB=5.
∴结论“AD=5”正确.
⑤∵点D与点E关于AC对称,
点D与点F关于BC对称,
∴当点D从点A运动到点B时,
点E的运动路径AM与AB关于AC对称,
点F的运动路径NB与AB关于BC对称.
∴EF扫过的图形就是图5中阴影部分.
∴S阴影=2S△ABC
=2×AC BC
=AC BC
=5×5=25.
∴EF扫过的面积为25.
∴结论“EF扫过的面积为20”错误.
故答案为:①、②、④.
10.解:连接AD,OB,OP;
∵PA、PB与⊙O分别相切于点A、点B,
∴∠OAP=∠OBP=90°,∠AOB=180°﹣∠P=120°,
∴∠AOP=60°,AP=AOtan60°=,
∴PC=;
∵PA2=PD PC,
∴PD=,
∴CD=.
11.解:延长ID到M,使得DM=ID,连接CM.
∵I是△ABC的内心,
∴∠IAC=∠IAB,∠ICA=∠ICB,
∵∠DIC=∠IAC+∠ICA,∠DCI=∠BCD+∠ICB,∠BCD=∠IAB,
∴∠DIC=∠DCI,
∴DI=DC=DM,
∴∠ICM=90°,
∴CM==8,
∵AI=2CD=10,
∴AI=IM,∵AE=EC,
∴IE=CM=4,
故答案为4.
12.解:设⊙I切AC与M,切BC于N,半径为r,
则AD=AM,CM=CN=r,BD=BN,r=(AC+BC﹣AB),
∵AB为半圆的直径,
∴∠ACB=90°,
∴AB2=AC2+BC2,
∴AD DB=AM BN=(AC﹣r)(BC﹣r)=[AC﹣(AC+BC﹣AB)][BC﹣(AC+BC﹣AB)]
=(AC﹣BC+AB)(AB+BC﹣AC)=(AB2﹣AC2﹣BC2+2AC BC)=AC BC,
由射影定理得AD DB=DE2=81,
∴S△ABC=AC BC=81,
故答案为:81.
三.解答题(共8小题,满分60分)
13.解:(1)△ABC是等腰三角形,理由是:
如图1,连接OE,
∵DE是⊙O的切线,
∴OE⊥DE,
∵ED⊥AC,
∴AC∥OE,
∴∠1=∠C,
∵OB=OE,
∴∠1=∠B,
∴∠B=∠C,
∴△ABC是等腰三角形;
(2)如图2,过点O作OG⊥AC,垂足为G,则得四边形OGDE是矩形,
∵△ABC是等腰三角形,
∴∠B=∠C=75°,
∴∠A=180°﹣75°﹣75°=30°,
设OG=x,则OA=OB=OE=2x,AG=x,
∴DG=OE=2x,
根据AC=AB得:4x=x+2x+2﹣,
x=1,
∴OE=OB=2,
在直角△OEF中,∠EOF=∠A=30°,
cos30=,OF==2÷=,
∴BF=﹣2,⊙O的半径为2.
14.(1)证明:∵A(2,0)D(0,4),
∴AO=2,OD=4,
∴在Rt△ADO中,tan∠ADO===,
∵tan∠APD=,
∴∠ADO=∠APD,
∵∠AOD=90°,
∴∠ADO+∠DAO=90°,
∴∠DAO+∠APD=90°,
∴∠PDA=180°﹣90°=90°,
∴AD⊥PD,
∵AD是⊙A的半径,
∴PD是⊙A的切线.
(2)解:在△ADO中,OA=2,OD=4,由勾股定理得:AD=2,
在Rt△PDA中,tan∠APD==,
即PD=4,
由勾股定理得:AP==10,
∵OA=2,
∴OP=8,
即P(﹣8,0),
∵D(0,4),
∴设直线PD的解析式是:y=kx+4,
把P的坐标代入得:0=﹣8k+4,
解得:k=,
∴直线PD的解析式是y=x+4,
假如存在M点,使得S△MOD=2S△AOD,
设M的坐标是(x,x+4),
如图:
当M在y轴的左边时,过M作MN⊥OD于N,
∵S△MOD=2S△AOD,
∴×4×(﹣x)=2××2×4,
解得:x=﹣4,
y=x+4=2,
即此时M坐标是(﹣4,2),
当M点在y轴的右边时,同法可求M的横坐标是4,代入y=x+4得y=6,
此时M的坐标是(4,6),
即在直线PD上存在点M,使得S△MOD=2S△AOD,点M的坐标是(﹣4,2)或(4,6).
15.(1)证明:∵BD是⊙O的切线,
∴∠DBA=90°,
∵CH⊥AB,
∴CH∥BD,
∴△AEC∽△AFD,
∴=,
∴AE FD=AF EC.
(2)证明:连接OC,BC,
∵CH∥BD,
∴△AEC∽△AFD,△AHE∽△ABF,
∴=,=,
∴==,
∵CE=EH(E为CH中点),
∴BF=DF,
∵AB为⊙O的直径,
∴∠ACB=∠DCB=90°,
∵BF=DF,
∴CF=DF=BF(直角三角形斜边上的中线等于斜边的一半),
即CF=BF.
(3)解:连接OF,
∵FE=FB=2,
∴FC=FE=2,
∴∠FEC=∠FCE,
∵∠FCE+∠G=∠FEC+∠FAB=90°,
∴∠FAB=∠G,
∴FA=FG,
∴AB=BG,
∵AO=OB,BF=DF,
∴OF∥AC,
∴==3,
∴FG=3FC=6,
∴由勾股定理得:BG===4,
∴OA=OB=AB=BG=2,
即⊙O的半径r的长为2.
16.证明:(1)∵CB=CE,
∴∠E=∠CBE.
∵CG为⊙O切线,
∴∠BCD=∠E.
∴∠CBE=∠BCD.
∴BE∥DG.
(2)∵∠A=∠E,
∴∠A=∠CBE.
∵∠ACB=∠ACB,
∴△CBF∽△CAB,.
∴CB2=CF AC=CF (CF+AF)=CF2+CF AF.
即CB2﹣CF2=AF CF.
由相交弦定理,得AF CF=BF FE.
∴CB2﹣CF2=BF FE.
17.证明:连PO交ST于点D,则PO⊥ST;
连SO,作OE⊥PB于E,则E为AB中点,
于是
因为C、E、O、D四点共圆,
所以PC PE=PD PO
又因为Rt△SPD∽Rt△OPS
所以
即PS2=PD PO
而由切割线定理知PS2=PA PB
所以
即
18.解:(1)连接OA.结论:△ABC为等腰三角形,
理由:∵=,
∴∠EOF=∠DOE,
又∵∠EOF+∠C=180°,∠DOE+∠B=180°,
∴∠C=∠B,
∴AB=AC,
∴△ABC为等腰三角形;
(2)连接OB、OC、OD、OF,如图,
∵等腰三角形ABC中,AE⊥BC,
∴E是BC中点,BE=CE,
在Rt△AOF和Rt△AOD中,
,
∴Rt△AOF≌Rt△AOD,
∴AF=AD,
同理Rt△COF≌Rt△COE,CF=CE=2,
Rt△BOD≌Rt△BOE,BD=BE,
∴AD=AF,BD=CF,
∴DF∥BC,
∴=,
∵AE==4,
∴AM=4×=.
19.证明:(1)∵AD与△ABC的外接圆⊙O恰好相切于点A,
∴∠ABE=∠DAE,又∠EAC=∠EBC,
∴∠DAC=∠ABC,
∵AD∥BC,
∴∠DAC=∠ACB,
∴∠ABC=∠ACB,
∴AB=AC;
(2)作AF⊥CD于F,
∵四边形ABCE是圆内接四边形,
∴∠ABC=∠AEF,又∠ABC=∠ACB,
∴∠AEF=∠ACB,又∠AEB=∠ACB,
∴∠AEH=∠AEF,
在△AEH和△AEF中,
,
∴△AEH≌△AEF,
∴EH=EF,
∴CE+EH=CF,
在△ABH和△ACF中,
,
∴△ABH≌△ACF,
∴BH=CF=CE+EH.
20.(1)证明:连接AN,
∵∠ABC=∠ACB,
∴AB=AC,
∵AC是⊙O的直径,
∴AN⊥BC,
∴∠CAN=∠BAN,BN=CN,
∵∠CAB=2∠BCP,
∴∠CAN=∠BCP.
∵∠CAN+∠ACN=90°,
∴∠BCP+∠ACN=90°,
∴CP⊥AC
∵OC是⊙O的半径
∴CP是⊙O的切线;
(2)解:∵∠ANC=90°,sin∠BCP=,
∴=,
∴AC=5,
∴⊙O的半径为
如图,过点B作BD⊥AC于点D.
由(1)得BN=CN=BC=,
在Rt△CAN中,AN==2,
在△CAN和△CBD中,
∠ANC=∠BDC=90°,∠ACN=∠BCD,
∴△CAN∽△CBD,
∴=,
∴BD=4.
在Rt△BCD中,CD==2,
∴AD=AC﹣CD=5﹣2=3,
∵BD∥CP,
∴=,=
∴CP=,BP=
∴△APC的周长是AC+PC+AP=20.
