2021-2022学年数学人教B版(2019)选择性必修第一册第一章空间向量与立体几何达标检测
文档属性
| 名称 | 2021-2022学年数学人教B版(2019)选择性必修第一册第一章空间向量与立体几何达标检测 |  | |
| 格式 | docx | ||
| 文件大小 | 459.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教B版(2019) | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-18 15:10:35 | ||
图片预览




文档简介
本章达标检测
(满分:150分;时间:120分钟)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图,在三棱柱ABC-A1B1C1中,M为A1C1的中点,若=a,=c,=b,则下列向量与相等的是( )
A.-a+b+c B.a+b+c C.-a-b+c D.a-b+c
2.已知正方体ABCD-A1B1C1D1的棱长为a,且AC1与BD1相交于点O,则有( )
A.·=a2 B.·=a2 C.·=a D.·=a2
3.若平面α经过三点O(0,0,0),A(2,2,0),B(0,0,2),则平面α的法向量可以是( )
A.(1,0,1) B.(1,0,-1) C.(0,1,1) D.(-1,1,0)
4.设u=(2,2,-1)是平面α的一个法向量,a=(-3,4,2)是直线l的一个方向向量,则直线l与平面α的位置关系是( )
A.平行或直线在平面内
B.垂直
C.相交但不垂直
D.不能确定
5.如图,已知正方形ABCD和正方形ADEF的边长均为6,且它们所在的平面互相垂直,O是BE的中点,=,则线段OM的长为( )
A.3 B.
C.2 D.
6.如图,在四棱锥P-ABCD中,侧面PAD是边长为4的正三角形,底面ABCD为正方形,侧面PAD⊥底面ABCD,若M为平面ABCD上的一个动点,且满足·=0,则点M到直线AB的最大距离为( )
A.2 B.3+ C.4+ D.4+2
7.在正方体ABCD-A1B1C1D1中,若F,G分别是棱AB,CC1的中点,则直线FG与平面A1ACC1所成角的正弦值为 ( )
A. B. C. D.
8.如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,AD∥BC,AB=AD=PD=1,BC=2,PD⊥平面ABCD,则二面角A-PB-C的大小为( )
A.30° B.60° C.120° D.150°
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多个选项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分)
9.下列命题中正确的是( )
A.A,B,M,N是空间中的四点,若,,不能构成空间向量的一组基底,则A,B,M,N四点共面
B.已知{a,b,c}为空间向量的一组基底,若m=a+c,则{a,b,m}也是空间向量的一组基底
C.若直线l的一个方向向量为e=(1,0,3),平面α的一个法向量为n=,则直线l∥α
D.若直线l的一个方向向量为e=(1,0,3),平面α的一个法向量为n=(-2,0,2),则直线l与平面α所成角的正弦值为
10.如图,一个结晶体的形状为平行六面体ABCD-A1B1C1D1,其中以顶点A为端点的三条棱长都相等,且它们彼此之间的夹角都是60°,则下列说法中正确的是( )
A.=2 B.·(-)=0
C.向量与的夹角是60° D.BD1与AC所成角的余弦值为
11.若将正方形ABCD沿对角线BD折成直二面角,则下列结论正确的有( )
A.AD与BC所成的角为45°
B.AC与BD所成的角为90°
C.BC与平面ACD所成角的正弦值为
D.平面ABC与平面BCD所成角的正切值是
12.已知正方体ABCD-A1B1C1D1的棱长为1,E,F,G分别为棱BC,CC1,BB1的中点,则( )
A.直线D1D与直线AF垂直
B.直线A1G与平面AEF平行
C.平面AEF截正方体所得的截面面积为
D.点C和点G到平面AEF的距离相等
三、填空题(本大题共4小题,每小题5分,共20分.将答案填在题目中横线上)
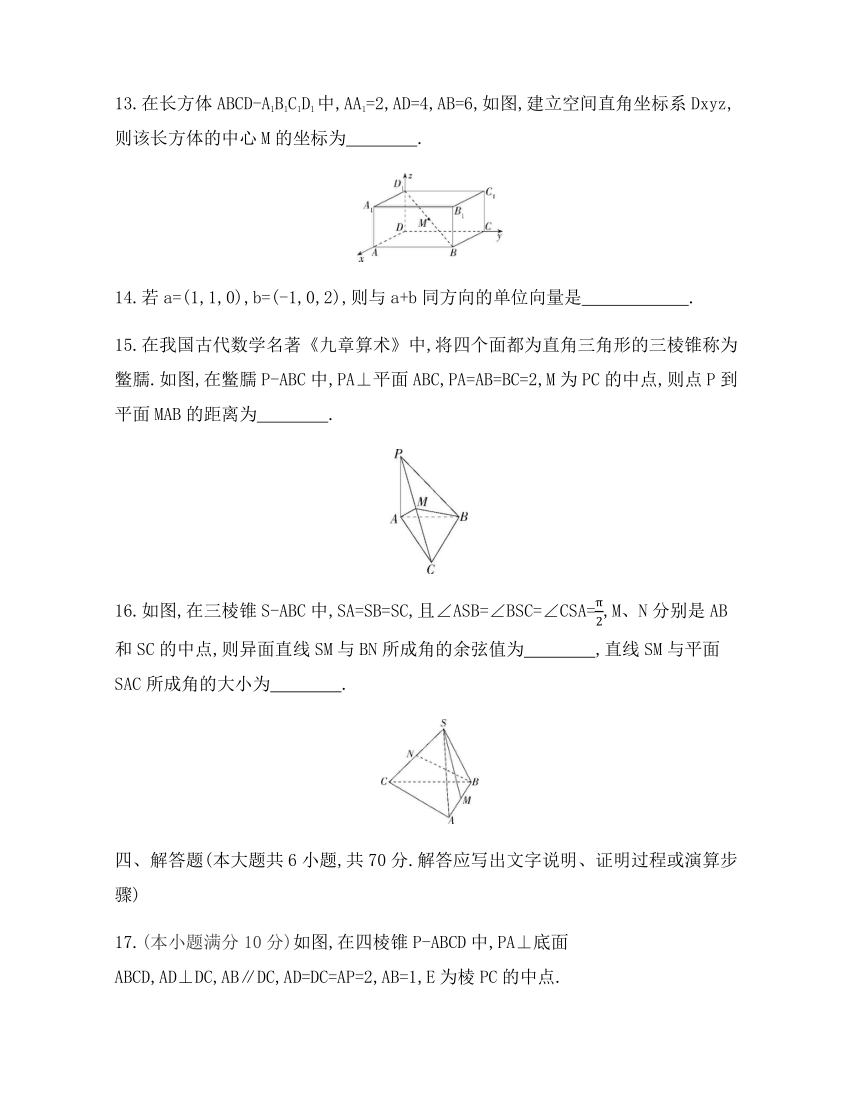
13.在长方体ABCD-A1B1C1D1中,AA1=2,AD=4,AB=6,如图,建立空间直角坐标系Dxyz,则该长方体的中心M的坐标为 .
14.若a=(1,1,0),b=(-1,0,2),则与a+b同方向的单位向量是 .
15.在我国古代数学名著《九章算术》中,将四个面都为直角三角形的三棱锥称为鳖臑.如图,在鳖臑P-ABC中,PA⊥平面ABC,PA=AB=BC=2,M为PC的中点,则点P到平面MAB的距离为 .
16.如图,在三棱锥S-ABC中,SA=SB=SC,且∠ASB=∠BSC=∠CSA=,M、N分别是AB和SC的中点,则异面直线SM与BN所成角的余弦值为 ,直线SM与平面SAC所成角的大小为 .
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥DC,AB∥DC,AD=DC=AP=2,AB=1,E为棱PC的中点.
(1)证明:BE⊥PD;
(2)若F为棱PC上一点,满足BF⊥AC,求线段PF的长.
18.(本小题满分12分)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,BC∥AD,AB⊥BC,∠ADC=45°,PA⊥平面ABCD,AB=AP=1,AD=3.
(1)求异面直线PB与CD所成角的大小;
(2)求点D到平面PBC的距离.
19.(本小题满分12分)如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是梯形,AB∥CD,BC⊥CD,AB=PD=4,CD=2,AD=2,M为CD的中点,N为PB上一点,且=λ(0<λ<1).
(1)当λ=时,求证:MN∥平面PAD;
(2)若直线AN与平面PBC所成角的正弦值为,求异面直线AD与CN所成角的余弦值.
20.(本小题满分12分)如图1,在边长为5的菱形ABCD中,AC=8,现沿对角线BD把△ABD折起,折起后(如图2)使∠ADC的余弦值为.
(1)求证:平面ABD⊥平面CBD;
(2)若M是AB的中点,求折起后AC与平面MCD所成角的正弦值.
21.(本小题满分12分)在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2.
(1)求证:CE∥平面PAD;
(2)在棱AB上是否存在一点F,使得平面DEF⊥平面PCE 如果存在,求的值;如果不存在,说明理由.
22.(本小题满分12分)如图,四棱锥P-ABCD的底面ABCD是直角梯形,AB∥DC,AD⊥DC,平面PDC⊥平面ABCD,△PDC是等边三角形,AB=AD=CD=1,E,F,G分别是棱PD,PC,BC的中点.
(1)求证:PA∥平面EFG;
(2)求二面角G-EF-D的大小;
(3)若线段PB上存在一点Q,使得PC⊥平面ADQ,且=λ,求λ的值.
答案全解全析
一、单项选择题
1.A =+=+(+)=+(+)=c+(-a+b)=-a+b+c.
2.B 对于A,·=·(+)=+·=a2,故A错误;
对于B,·=·(++)=+·+·==a2,故B正确;
对于C,·=·=·=a2,故C错误;
对于D,·=·(-)=·-=-a2,所以D错误.
故选B.
3.D 设平面α的法向量为n,对于A选项,n·=2,故A选项错误;对于B选项,n·=-2,故B选项错误;对于C选项,n·=2,故C选项错误;对于D选项,由于n·=0,n·=0,且不共线向量,有共同的始点,故D选项正确.故选D.
4.A 因为u·a=2×(-3)+2×4-1×2=0,所以u⊥a,故直线l∥平面α或直线l 平面α.故选A.
5.B 由题意可得DA,DC,DE两两互相垂直.以D为坐标原点,,,的方向分别为x轴、y轴、z轴正方向,建立如图所示的空间直角坐标系,
则E(0,0,6),F(6,0,6),B(6,6,0).
因为O是BE的中点,所以O(3,3,3).
因为=,所以M(6,0,4),所以||==,即线段OM的长为.故选B.
导师点睛 本题考查空间中两点间的距离公式的应用,解题的关键在于建立合适的空间直角坐标系,并求出相应点的坐标.
6.B 以D为原点,DA所在直线为x轴,DC所在直线为y轴,过D作平面ABCD的垂线为z轴,建立如图所示的空间直角坐标系,则P(2,0,2),C(0,4,0).
设M(a,b,0),
则=(2-a,-b,2),=(-a,4-b,0).
∵·=0,
∴(2-a,-b,2)·(-a,4-b,0)=-2a+a2-4b+b2=0,整理得(a-1)2+(b-2)2=5,
∴M为平面ABCD上到点(1,2)的距离为的一个动点,
故点M到直线AB的最大距离为4-1+=3+.故选B.
7.D 解法一:过F作BD的平行线交AC于点M,连接MG,易证得FM⊥平面A1ACC1,所以FM⊥MG,∠MGF即为直线FG与平面A1ACC1所成的角,
设正方体ABCD-A1B1C1D1的棱长为1,
易得FM=,FG=,
所以sin∠MGF==.
解法二:以A为原点,,,的方向分别为x轴、y轴、z轴正方向,建立如图所示的空间直角坐标系.
设正方体ABCD-A1B1C1D1的棱长为1,易得平面A1ACC1的一个法向量n=(-1,1,0),
F,G,
所以=.
设直线FG与平面A1ACC1所成的角为θ,
则sin θ=|cos|===.
8.C 取BC中点M,连接DM,由已知可得四边形ADMB为正方形,易得DM,DA,DP两两互相垂直,故以点D为原点,,,的方向分别为x轴、y轴、z轴正方向,建立如图所示的空间直角坐标系,则D(0,0,0),A(0,1,0),B(1,1,0),C(1,-1,0),P(0,0,1),所以=(0,-1,1),=(1,0,0),
设平面PAB的一个法向量为n1=(x,y,z),
则即
令z=1,则y=1,
所以n1=(0,1,1).
设平面PBC的一个法向量为n2=(a,b,c),易得=(0,-2,0),=(1,-1,-1),
所以
即
令c=1,则a=1,
所以n2=(1,0,1),
所以cos==.
易知二面角A-PB-C的平面角为钝角,
所以二面角A-PB-C的大小为120°.
故选C.
二、多项选择题
9.ABD 对于A,A,B,M,N是空间中的四点,若,,不能构成空间向量的一组基底,则,,共面,则A,B,M,N四点共面,故A正确;
对于B,已知{a,b,c}为空间向量的一组基底,所以a,b,c不共面,若m=a+c,则a,b,m也不共面,故{a,b,m}也是空间向量的一组基底,故B正确;
对于C,因为e·n=1×(-2)+0×0+3×=0,所以e⊥n,所以l α或l∥α,故C错误;
对于D,因为cos===,所以直线l与平面α所成角的正弦值为,故D正确.
故选ABD.
10.AB 由题意可知平行六面体ABCD-A1B1C1D1的各棱长均相等,设棱长为1,则·=·=·=1×1×cos 60°= ,
所以=+++2·+2·+2·=1+1+1+3×2×=6,
而2=2=2(++2·)=2×=2×3=6, 所以A正确.
·(-)=(++)·(-)=·-·+-·+·- =0,所以B正确.
向量=,显然△AA1D 为等边三角形,故∠AA1D=60°,所以向量与的夹角是120°,即向量与的夹角是120°,所以C不正确.
因为=+-,=+ ,
所以||==,||==,
·=(+-)·(+)=1,
所以cos<,>===,所以D不正确.
故选AB.
11.BCD 取BD中点O,连接AO,CO.
若将正方形ABCD沿对角线BD折成直二面角,则OA⊥BD,OC⊥BD,OA⊥OC,
∴以O为原点,OC所在直线为x轴,OD所在直线为y轴,OA所在直线为z轴,建立如图所示的空间直角坐标系.
设OC=1,则A(0,0,1),B(0,-1,0),C(1,0,0),D(0,1,0),
∴=(0,1,-1),=(1,1,0),
∴cos<,>===,
∴AD与BC所成的角为60°,故A不正确;
易得=(1,0,-1),=(0,2,0),
∵·=0,∴AC⊥BD,故B正确;
设平面ACD的一个法向量为t=(x,y,z),
则取z=1,则x=y=1,
∴t=(1,1,1),又=(1,1,0),
设BC与平面ACD所成的角为θ,
∴sin θ=|cos<,t>|===,故C正确;
易知平面BCD的一个法向量n=(0,0,1),=(0,1,1),=(1,1,0),
设平面ABC的一个法向量为m=(x',y',z'),
则取x'=1,则y'=-1,z'=1,∴m=(1,-1,1),
设平面ABC与平面BCD所成的角为α,则cos α=|cos|==,
∴sin α=,tan α=,
∴平面ABC与平面BCD所成角的正切值是,故D正确.故选BCD.
12.BC 对于选项A,(解法一)以D点为坐标原点,DA、DC、DD1所在的直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则D(0,0,0),A(1,0,0),A1(1,0,1),E,F,G,D1(0,0,1).
从而=(0,0,1),=,
从而·=≠0,所以直线DD1与直线AF不垂直,故选项A错误.
(解法二)取DD1的中点N,连接AN,则AN为直线AF在平面ADD1A1内的射影,AN与DD1不垂直,从而AF与DD1也不垂直,故选项A错误.
对于选项B,由上述解法一中所建坐标系可得,=,=,=,设=x+y,则解得
∴=2-,∴,,共面,又A1G 平面AEF,
∴直线A1G与平面AEF平行,故选项B正确.
对于选项C,连接AD1,D1F,延长AE,交D1F的延长线于H.易知四边形AEFD1为平面AEF截正方体所得的截面四边形(如图所示),
易知D1H=AH=,AD1=,
所以=××=,
而==,故选项C正确.
对于选项D,(解法一)连接AG,EG,FG,如图.
由于S△GEF=S梯形BEFG-S△EBG=××-××=,
而S△ECF=××=,
所以S△GEF=2S△ECF.
又VA-GEF=S△GEF·AB,
VA-ECF=S△ECF·AB,
所以VA-GEF=2VA-ECF,
即VG-AEF=2VC-AEF,所以点G到平面AEF的距离为点C到平面AEF的距离的二倍,故选项D错误.
(解法二)连接CG,假设点C与点G到平面AEF的距离相等,则平面AEF将CG平分,则平面AEF必过CG的中点,设CG与EF的交点为O,易知O不是CG的中点,所以假设不成立,故选项D错误.
三、填空题
13.答案 (2,3,1)
解析 由题意得B(4,6,0),D1(0,0,2),
易知M是BD1的中点,
所以点M的坐标为(2,3,1).
14.答案
解析 与a+b同方向的单位向量是(0,1,2)=.
15.答案
解析 易知PA⊥AB,PA⊥BC,AB⊥BC,故以B为坐标原点,BA,BC所在直线分别为x轴,y轴,过点B且与平面ABC垂直的直线为z轴,建立如图所示的空间直角坐标系,
则B(0,0,0),A(2,0,0),P(2,0,2),C(0,2,0),由M为PC的中点可得M(1,1,1),
=(1,1,1),=(2,0,0), =(2,0,2).
设n=(x,y,z)为平面MBA的一个法向量,则即
令z=-1,则y=1,所以n=(0,1,-1),所以点P到平面MAB的距离d==.
16.答案 ;
解析 因为∠ASB=∠BSC=∠CSA=,所以以S为坐标原点,,,的方向分别为x轴、y轴、z轴正方向建立空间直角坐标系.设SA=SB=SC=2,则S(0,0,0),B(0,2,0),A(2,0,0),C(0,0,2),M(1,1,0),N(0,0,1),
所以=(1,1,0),=(0,-2,1),所以cos<,>==-,所以异面直线SM与BN所成的角的余弦值为.
易得平面SAC一个法向量为=(0,2,0),则由cos<,>==得<,>=,所以直线SM与平面SAC所成角的大小为.
四、解答题
17.解析 (1)证明:易得AB,AD,AP两两互相垂直,故以A为原点,,,的方向分别为x轴、y轴、z轴正方向,建立如图所示的空间直角坐标系,
则A(0,0,0),B(1,0,0),P(0,0,2),C(2,2,0),E(1,1,1),D(0,2,0),
∴=(0,1,1),=(0,2,-2),
∴·=0,
∴BE⊥PD.(5分)
(2)由(1)可得=(1,2,0),=(-2,-2,2),=(2,2,0),
由点F在棱PC上,设=λ=(-2λ,-2λ,2λ),0≤λ≤1,
∴=+=(1-2λ,2-2λ,2λ).
∵BF⊥AC,∴·=2(1-2λ)+2(2-2λ)=0,解得λ=,
∴||=||==,
即线段PF的长为.(10分)
18.解析 (1)易得AB,AD,AP两两互相垂直,故以A为原点,,,的方向分别为x轴,y轴,z轴正方向,建立如图所示的空间直角坐标系,
则P(0,0,1),B(1,0,0),C(1,2,0),D(0,3,0),(2分)
所以=(1,0,-1),=(-1,1,0).
设异面直线PB与CD所成的角为θ,
则cos θ==,(4分)
所以异面直线PB与CD所成角的大小为. (6分)
(2)设平面PBC的一个法向量为n=(u,v,w),由(1)可得=(0,2,0),
则即
取u=w=1,得n=(1,0,1),(9分)
所以点D到平面PBC的距离d==.(12分)
19.解析 (1)证明:当λ=时,=,在PA上取=,连接EN,DE.
∵=,=,AB=4,
∴EN∥AB,且EN=AB=1.
∵M为CD的中点,CD=2,
∴DM=CD=1.
又∵AB∥CD,∴EN∥DM,EN=DM,
∴四边形DMNE是平行四边形,
∴MN∥DE,
又∵DE 平面PAD,MN 平面PAD,
∴MN∥平面PAD.(5分)
(2)过点D作DH⊥AB于H,则DH⊥CD,故DH,DC,DP两两互相垂直.以D为坐标原点,,,的方向分别为x轴、y轴、z轴正方向,建立如图所示的空间直角坐标系Dxyz,(6分)
则D(0,0,0),C(0,2,0),B(2,2,0),A(2,-2,0),P(0,0,4),
∴=(2,0,0),=(0,-2,4),=(-2,2,4),=(2,2,-4),
则=+=+λ=(-2,2,4)+λ(2,2,-4)=(2λ-2,2λ+2,4-4λ).
设平面PBC的一个法向量为n=(x,y,z),则即令z=1,则y=2,x=0,∴n=(0,2,1).(9分)
设直线AN与平面PBC所成的角为θ,则
sin θ=|cos<,n>|===,
解得λ=或λ=1(舍去),
则N,=,-,,
设异面直线AD与CN所成的角为α,
易知=(-2,2,0),
所以cos α=|cos<,>|==,
所以异面直线AD与CN所成角的余弦值为.(12分)
20.解析 (1)证明:在菱形ABCD中,记AC,BD的交点为O,
则OA=OC=4,∵AD=5,∴OB=OD=3.
将△ABD折起后变成三棱锥A-BCD,在△ACD中,
AC2=AD2+CD2-2AD·CDcos∠ADC=25+25-2×5×5×=32.
在△AOC中,OA2+OC2=32=AC2,
∴∠AOC=90°,即AO⊥CO.
又AO⊥BO,BO∩CO=O,
∴AO⊥平面CBD.
又AO 平面ABD,
∴平面ABD⊥平面CBD.(5分)
(2)由(1)知OC,OD,OA两两互相垂直,故以O为原点,,,的方向分别为x轴、y轴、z轴正方向,建立如图所示的空间直角坐标系Oxyz,(7分)
则A(0,0,4),B(0,-3,0),C(4,0,0),D(0,3,0),M,(8分)
∴=,=(4,-3,0),=(4,0,-4).
设平面MCD的一个法向量为n=(x,y,z),
则即
取y=4,则x=3,z=9,∴n=(3,4,9).(10分)
设AC与平面MCD所成的角为θ,
则sin θ=|cos<,n>|===,
∴AC与平面MCD所成角的正弦值为. (12分)
21.解析 (1)证明:取PA的中点G,连接EG,DG.
因为PA∥BE,且PA=4,BE=2,所以BE∥AG,且BE=AG,
所以四边形BEGA为平行四边形,所以EG∥AB,且EG=AB.
因为四边形ABCD是正方形,所以CD∥AB,CD=AB,
所以EG∥CD,且EG=CD,
所以四边形CDGE为平行四边形,所以CE∥DG.
因为DG 平面PAD,CE 平面PAD,所以CE∥平面PAD.(4分)
(2)易得AB,AD,AP两两互相垂直,故以A为原点,,,的方向分别为x轴、y轴、z轴正方向,建立如图所示的空间直角坐标系,则B(4,0,0),C(4,4,0),E(4,0,2),P(0,0,4),D(0,4,0),(5分)
所以=(4,4,-4),=(4,0,-2),=(0,4,-4).
设平面PCE的一个法向量为m=(x,y,z),
则
令x=1,则y=1,z=2,所以m=(1,1,2).(8分)
假设存在点F(a,0,0)(0≤a≤4)满足题意,如图,连接EF,DF,DE,则=(4-a,0,2),=(4,-4,2).
设平面DEF的一个法向量为n=(x',y',z'),
则
令x'=2,则y'=,z'=a-4,
所以n=.(10分)
因为平面DEF⊥平面PCE,所以m·n=0,即2++2a-8=0,所以a=,故存在点F满足题意,此时=.(12分)
22.解析 (1)证明:取AD的中点H,连接EH,GH.
∵E,F,G,H分别是PD,PC,BC,AD的中点,
∴EF∥CD,GH∥CD,EH∥PA,
∴EF∥GH.
∴E,F,G,H四点共面.
∵PA∥EH,PA 平面EFG,EH 平面EFG,∴PA∥平面EFG.(4分)
(2)∵平面PDC ⊥平面ABCD,平面PDC∩平面ABCD=DC,AD⊥DC,∴AD⊥平面PDC.
以DA,DC所在直线分别为x轴,y轴,过点D且与平面ABCD垂直的直线为z轴,建立如图所示的空间直角坐标系Dxyz,
则G,E,F,
∴=(0,1,0),=,
易得平面EFD的一个法向量m=(1,0,0).
设平面EFG的一个法向量为n=(x,y,z),
∴即
令x=,则z=1,
∴n=(,0,1).(7分)
∴cos===,
∴=30°,易知二面角G-EF-D的平面角为锐角,∴二面角G-EF-D的大小为30°.(8分)
(3)易得P(0,1,),B(1,1,0),A(1,0,0),C(0,2,0),设Q(a,b,c),
则=(0,1,-),=(1,0,-),
=(a,b-1,c-)=λ=λ(1,0,-)=(λ,0,-λ),
∴Q(λ,1,-λ),=(λ-1,1,-λ).(10分)
∵PC⊥平面ADQ,∴PC⊥AQ,
∴·=1-(-λ)=0,解得λ=,满足题意.(12分)
(满分:150分;时间:120分钟)
一、单项选择题(本大题共8小题,每小题5分,共40分.在每小题给出的四个选项中,只有一项是符合题目要求的)
1.如图,在三棱柱ABC-A1B1C1中,M为A1C1的中点,若=a,=c,=b,则下列向量与相等的是( )
A.-a+b+c B.a+b+c C.-a-b+c D.a-b+c
2.已知正方体ABCD-A1B1C1D1的棱长为a,且AC1与BD1相交于点O,则有( )
A.·=a2 B.·=a2 C.·=a D.·=a2
3.若平面α经过三点O(0,0,0),A(2,2,0),B(0,0,2),则平面α的法向量可以是( )
A.(1,0,1) B.(1,0,-1) C.(0,1,1) D.(-1,1,0)
4.设u=(2,2,-1)是平面α的一个法向量,a=(-3,4,2)是直线l的一个方向向量,则直线l与平面α的位置关系是( )
A.平行或直线在平面内
B.垂直
C.相交但不垂直
D.不能确定
5.如图,已知正方形ABCD和正方形ADEF的边长均为6,且它们所在的平面互相垂直,O是BE的中点,=,则线段OM的长为( )
A.3 B.
C.2 D.
6.如图,在四棱锥P-ABCD中,侧面PAD是边长为4的正三角形,底面ABCD为正方形,侧面PAD⊥底面ABCD,若M为平面ABCD上的一个动点,且满足·=0,则点M到直线AB的最大距离为( )
A.2 B.3+ C.4+ D.4+2
7.在正方体ABCD-A1B1C1D1中,若F,G分别是棱AB,CC1的中点,则直线FG与平面A1ACC1所成角的正弦值为 ( )
A. B. C. D.
8.如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,∠BAD=90°,AD∥BC,AB=AD=PD=1,BC=2,PD⊥平面ABCD,则二面角A-PB-C的大小为( )
A.30° B.60° C.120° D.150°
二、多项选择题(本大题共4小题,每小题5分,共20分.在每小题给出的选项中,有多个选项符合题目要求,全部选对的得5分,有选错的得0分,部分选对的得2分)
9.下列命题中正确的是( )
A.A,B,M,N是空间中的四点,若,,不能构成空间向量的一组基底,则A,B,M,N四点共面
B.已知{a,b,c}为空间向量的一组基底,若m=a+c,则{a,b,m}也是空间向量的一组基底
C.若直线l的一个方向向量为e=(1,0,3),平面α的一个法向量为n=,则直线l∥α
D.若直线l的一个方向向量为e=(1,0,3),平面α的一个法向量为n=(-2,0,2),则直线l与平面α所成角的正弦值为
10.如图,一个结晶体的形状为平行六面体ABCD-A1B1C1D1,其中以顶点A为端点的三条棱长都相等,且它们彼此之间的夹角都是60°,则下列说法中正确的是( )
A.=2 B.·(-)=0
C.向量与的夹角是60° D.BD1与AC所成角的余弦值为
11.若将正方形ABCD沿对角线BD折成直二面角,则下列结论正确的有( )
A.AD与BC所成的角为45°
B.AC与BD所成的角为90°
C.BC与平面ACD所成角的正弦值为
D.平面ABC与平面BCD所成角的正切值是
12.已知正方体ABCD-A1B1C1D1的棱长为1,E,F,G分别为棱BC,CC1,BB1的中点,则( )
A.直线D1D与直线AF垂直
B.直线A1G与平面AEF平行
C.平面AEF截正方体所得的截面面积为
D.点C和点G到平面AEF的距离相等
三、填空题(本大题共4小题,每小题5分,共20分.将答案填在题目中横线上)
13.在长方体ABCD-A1B1C1D1中,AA1=2,AD=4,AB=6,如图,建立空间直角坐标系Dxyz,则该长方体的中心M的坐标为 .
14.若a=(1,1,0),b=(-1,0,2),则与a+b同方向的单位向量是 .
15.在我国古代数学名著《九章算术》中,将四个面都为直角三角形的三棱锥称为鳖臑.如图,在鳖臑P-ABC中,PA⊥平面ABC,PA=AB=BC=2,M为PC的中点,则点P到平面MAB的距离为 .
16.如图,在三棱锥S-ABC中,SA=SB=SC,且∠ASB=∠BSC=∠CSA=,M、N分别是AB和SC的中点,则异面直线SM与BN所成角的余弦值为 ,直线SM与平面SAC所成角的大小为 .
四、解答题(本大题共6小题,共70分.解答应写出文字说明、证明过程或演算步骤)
17.(本小题满分10分)如图,在四棱锥P-ABCD中,PA⊥底面ABCD,AD⊥DC,AB∥DC,AD=DC=AP=2,AB=1,E为棱PC的中点.
(1)证明:BE⊥PD;
(2)若F为棱PC上一点,满足BF⊥AC,求线段PF的长.
18.(本小题满分12分)如图,在四棱锥P-ABCD中,底面ABCD为直角梯形,BC∥AD,AB⊥BC,∠ADC=45°,PA⊥平面ABCD,AB=AP=1,AD=3.
(1)求异面直线PB与CD所成角的大小;
(2)求点D到平面PBC的距离.
19.(本小题满分12分)如图,在四棱锥P-ABCD中,PD⊥底面ABCD,底面ABCD是梯形,AB∥CD,BC⊥CD,AB=PD=4,CD=2,AD=2,M为CD的中点,N为PB上一点,且=λ(0<λ<1).
(1)当λ=时,求证:MN∥平面PAD;
(2)若直线AN与平面PBC所成角的正弦值为,求异面直线AD与CN所成角的余弦值.
20.(本小题满分12分)如图1,在边长为5的菱形ABCD中,AC=8,现沿对角线BD把△ABD折起,折起后(如图2)使∠ADC的余弦值为.
(1)求证:平面ABD⊥平面CBD;
(2)若M是AB的中点,求折起后AC与平面MCD所成角的正弦值.
21.(本小题满分12分)在如图所示的几何体中,四边形ABCD为正方形,PA⊥平面ABCD,PA∥BE,AB=PA=4,BE=2.
(1)求证:CE∥平面PAD;
(2)在棱AB上是否存在一点F,使得平面DEF⊥平面PCE 如果存在,求的值;如果不存在,说明理由.
22.(本小题满分12分)如图,四棱锥P-ABCD的底面ABCD是直角梯形,AB∥DC,AD⊥DC,平面PDC⊥平面ABCD,△PDC是等边三角形,AB=AD=CD=1,E,F,G分别是棱PD,PC,BC的中点.
(1)求证:PA∥平面EFG;
(2)求二面角G-EF-D的大小;
(3)若线段PB上存在一点Q,使得PC⊥平面ADQ,且=λ,求λ的值.
答案全解全析
一、单项选择题
1.A =+=+(+)=+(+)=c+(-a+b)=-a+b+c.
2.B 对于A,·=·(+)=+·=a2,故A错误;
对于B,·=·(++)=+·+·==a2,故B正确;
对于C,·=·=·=a2,故C错误;
对于D,·=·(-)=·-=-a2,所以D错误.
故选B.
3.D 设平面α的法向量为n,对于A选项,n·=2,故A选项错误;对于B选项,n·=-2,故B选项错误;对于C选项,n·=2,故C选项错误;对于D选项,由于n·=0,n·=0,且不共线向量,有共同的始点,故D选项正确.故选D.
4.A 因为u·a=2×(-3)+2×4-1×2=0,所以u⊥a,故直线l∥平面α或直线l 平面α.故选A.
5.B 由题意可得DA,DC,DE两两互相垂直.以D为坐标原点,,,的方向分别为x轴、y轴、z轴正方向,建立如图所示的空间直角坐标系,
则E(0,0,6),F(6,0,6),B(6,6,0).
因为O是BE的中点,所以O(3,3,3).
因为=,所以M(6,0,4),所以||==,即线段OM的长为.故选B.
导师点睛 本题考查空间中两点间的距离公式的应用,解题的关键在于建立合适的空间直角坐标系,并求出相应点的坐标.
6.B 以D为原点,DA所在直线为x轴,DC所在直线为y轴,过D作平面ABCD的垂线为z轴,建立如图所示的空间直角坐标系,则P(2,0,2),C(0,4,0).
设M(a,b,0),
则=(2-a,-b,2),=(-a,4-b,0).
∵·=0,
∴(2-a,-b,2)·(-a,4-b,0)=-2a+a2-4b+b2=0,整理得(a-1)2+(b-2)2=5,
∴M为平面ABCD上到点(1,2)的距离为的一个动点,
故点M到直线AB的最大距离为4-1+=3+.故选B.
7.D 解法一:过F作BD的平行线交AC于点M,连接MG,易证得FM⊥平面A1ACC1,所以FM⊥MG,∠MGF即为直线FG与平面A1ACC1所成的角,
设正方体ABCD-A1B1C1D1的棱长为1,
易得FM=,FG=,
所以sin∠MGF==.
解法二:以A为原点,,,的方向分别为x轴、y轴、z轴正方向,建立如图所示的空间直角坐标系.
设正方体ABCD-A1B1C1D1的棱长为1,易得平面A1ACC1的一个法向量n=(-1,1,0),
F,G,
所以=.
设直线FG与平面A1ACC1所成的角为θ,
则sin θ=|cos
8.C 取BC中点M,连接DM,由已知可得四边形ADMB为正方形,易得DM,DA,DP两两互相垂直,故以点D为原点,,,的方向分别为x轴、y轴、z轴正方向,建立如图所示的空间直角坐标系,则D(0,0,0),A(0,1,0),B(1,1,0),C(1,-1,0),P(0,0,1),所以=(0,-1,1),=(1,0,0),
设平面PAB的一个法向量为n1=(x,y,z),
则即
令z=1,则y=1,
所以n1=(0,1,1).
设平面PBC的一个法向量为n2=(a,b,c),易得=(0,-2,0),=(1,-1,-1),
所以
即
令c=1,则a=1,
所以n2=(1,0,1),
所以cos
易知二面角A-PB-C的平面角为钝角,
所以二面角A-PB-C的大小为120°.
故选C.
二、多项选择题
9.ABD 对于A,A,B,M,N是空间中的四点,若,,不能构成空间向量的一组基底,则,,共面,则A,B,M,N四点共面,故A正确;
对于B,已知{a,b,c}为空间向量的一组基底,所以a,b,c不共面,若m=a+c,则a,b,m也不共面,故{a,b,m}也是空间向量的一组基底,故B正确;
对于C,因为e·n=1×(-2)+0×0+3×=0,所以e⊥n,所以l α或l∥α,故C错误;
对于D,因为cos
故选ABD.
10.AB 由题意可知平行六面体ABCD-A1B1C1D1的各棱长均相等,设棱长为1,则·=·=·=1×1×cos 60°= ,
所以=+++2·+2·+2·=1+1+1+3×2×=6,
而2=2=2(++2·)=2×=2×3=6, 所以A正确.
·(-)=(++)·(-)=·-·+-·+·- =0,所以B正确.
向量=,显然△AA1D 为等边三角形,故∠AA1D=60°,所以向量与的夹角是120°,即向量与的夹角是120°,所以C不正确.
因为=+-,=+ ,
所以||==,||==,
·=(+-)·(+)=1,
所以cos<,>===,所以D不正确.
故选AB.
11.BCD 取BD中点O,连接AO,CO.
若将正方形ABCD沿对角线BD折成直二面角,则OA⊥BD,OC⊥BD,OA⊥OC,
∴以O为原点,OC所在直线为x轴,OD所在直线为y轴,OA所在直线为z轴,建立如图所示的空间直角坐标系.
设OC=1,则A(0,0,1),B(0,-1,0),C(1,0,0),D(0,1,0),
∴=(0,1,-1),=(1,1,0),
∴cos<,>===,
∴AD与BC所成的角为60°,故A不正确;
易得=(1,0,-1),=(0,2,0),
∵·=0,∴AC⊥BD,故B正确;
设平面ACD的一个法向量为t=(x,y,z),
则取z=1,则x=y=1,
∴t=(1,1,1),又=(1,1,0),
设BC与平面ACD所成的角为θ,
∴sin θ=|cos<,t>|===,故C正确;
易知平面BCD的一个法向量n=(0,0,1),=(0,1,1),=(1,1,0),
设平面ABC的一个法向量为m=(x',y',z'),
则取x'=1,则y'=-1,z'=1,∴m=(1,-1,1),
设平面ABC与平面BCD所成的角为α,则cos α=|cos
∴sin α=,tan α=,
∴平面ABC与平面BCD所成角的正切值是,故D正确.故选BCD.
12.BC 对于选项A,(解法一)以D点为坐标原点,DA、DC、DD1所在的直线分别为x轴、y轴、z轴,建立如图所示的空间直角坐标系,则D(0,0,0),A(1,0,0),A1(1,0,1),E,F,G,D1(0,0,1).
从而=(0,0,1),=,
从而·=≠0,所以直线DD1与直线AF不垂直,故选项A错误.
(解法二)取DD1的中点N,连接AN,则AN为直线AF在平面ADD1A1内的射影,AN与DD1不垂直,从而AF与DD1也不垂直,故选项A错误.
对于选项B,由上述解法一中所建坐标系可得,=,=,=,设=x+y,则解得
∴=2-,∴,,共面,又A1G 平面AEF,
∴直线A1G与平面AEF平行,故选项B正确.
对于选项C,连接AD1,D1F,延长AE,交D1F的延长线于H.易知四边形AEFD1为平面AEF截正方体所得的截面四边形(如图所示),
易知D1H=AH=,AD1=,
所以=××=,
而==,故选项C正确.
对于选项D,(解法一)连接AG,EG,FG,如图.
由于S△GEF=S梯形BEFG-S△EBG=××-××=,
而S△ECF=××=,
所以S△GEF=2S△ECF.
又VA-GEF=S△GEF·AB,
VA-ECF=S△ECF·AB,
所以VA-GEF=2VA-ECF,
即VG-AEF=2VC-AEF,所以点G到平面AEF的距离为点C到平面AEF的距离的二倍,故选项D错误.
(解法二)连接CG,假设点C与点G到平面AEF的距离相等,则平面AEF将CG平分,则平面AEF必过CG的中点,设CG与EF的交点为O,易知O不是CG的中点,所以假设不成立,故选项D错误.
三、填空题
13.答案 (2,3,1)
解析 由题意得B(4,6,0),D1(0,0,2),
易知M是BD1的中点,
所以点M的坐标为(2,3,1).
14.答案
解析 与a+b同方向的单位向量是(0,1,2)=.
15.答案
解析 易知PA⊥AB,PA⊥BC,AB⊥BC,故以B为坐标原点,BA,BC所在直线分别为x轴,y轴,过点B且与平面ABC垂直的直线为z轴,建立如图所示的空间直角坐标系,
则B(0,0,0),A(2,0,0),P(2,0,2),C(0,2,0),由M为PC的中点可得M(1,1,1),
=(1,1,1),=(2,0,0), =(2,0,2).
设n=(x,y,z)为平面MBA的一个法向量,则即
令z=-1,则y=1,所以n=(0,1,-1),所以点P到平面MAB的距离d==.
16.答案 ;
解析 因为∠ASB=∠BSC=∠CSA=,所以以S为坐标原点,,,的方向分别为x轴、y轴、z轴正方向建立空间直角坐标系.设SA=SB=SC=2,则S(0,0,0),B(0,2,0),A(2,0,0),C(0,0,2),M(1,1,0),N(0,0,1),
所以=(1,1,0),=(0,-2,1),所以cos<,>==-,所以异面直线SM与BN所成的角的余弦值为.
易得平面SAC一个法向量为=(0,2,0),则由cos<,>==得<,>=,所以直线SM与平面SAC所成角的大小为.
四、解答题
17.解析 (1)证明:易得AB,AD,AP两两互相垂直,故以A为原点,,,的方向分别为x轴、y轴、z轴正方向,建立如图所示的空间直角坐标系,
则A(0,0,0),B(1,0,0),P(0,0,2),C(2,2,0),E(1,1,1),D(0,2,0),
∴=(0,1,1),=(0,2,-2),
∴·=0,
∴BE⊥PD.(5分)
(2)由(1)可得=(1,2,0),=(-2,-2,2),=(2,2,0),
由点F在棱PC上,设=λ=(-2λ,-2λ,2λ),0≤λ≤1,
∴=+=(1-2λ,2-2λ,2λ).
∵BF⊥AC,∴·=2(1-2λ)+2(2-2λ)=0,解得λ=,
∴||=||==,
即线段PF的长为.(10分)
18.解析 (1)易得AB,AD,AP两两互相垂直,故以A为原点,,,的方向分别为x轴,y轴,z轴正方向,建立如图所示的空间直角坐标系,
则P(0,0,1),B(1,0,0),C(1,2,0),D(0,3,0),(2分)
所以=(1,0,-1),=(-1,1,0).
设异面直线PB与CD所成的角为θ,
则cos θ==,(4分)
所以异面直线PB与CD所成角的大小为. (6分)
(2)设平面PBC的一个法向量为n=(u,v,w),由(1)可得=(0,2,0),
则即
取u=w=1,得n=(1,0,1),(9分)
所以点D到平面PBC的距离d==.(12分)
19.解析 (1)证明:当λ=时,=,在PA上取=,连接EN,DE.
∵=,=,AB=4,
∴EN∥AB,且EN=AB=1.
∵M为CD的中点,CD=2,
∴DM=CD=1.
又∵AB∥CD,∴EN∥DM,EN=DM,
∴四边形DMNE是平行四边形,
∴MN∥DE,
又∵DE 平面PAD,MN 平面PAD,
∴MN∥平面PAD.(5分)
(2)过点D作DH⊥AB于H,则DH⊥CD,故DH,DC,DP两两互相垂直.以D为坐标原点,,,的方向分别为x轴、y轴、z轴正方向,建立如图所示的空间直角坐标系Dxyz,(6分)
则D(0,0,0),C(0,2,0),B(2,2,0),A(2,-2,0),P(0,0,4),
∴=(2,0,0),=(0,-2,4),=(-2,2,4),=(2,2,-4),
则=+=+λ=(-2,2,4)+λ(2,2,-4)=(2λ-2,2λ+2,4-4λ).
设平面PBC的一个法向量为n=(x,y,z),则即令z=1,则y=2,x=0,∴n=(0,2,1).(9分)
设直线AN与平面PBC所成的角为θ,则
sin θ=|cos<,n>|===,
解得λ=或λ=1(舍去),
则N,=,-,,
设异面直线AD与CN所成的角为α,
易知=(-2,2,0),
所以cos α=|cos<,>|==,
所以异面直线AD与CN所成角的余弦值为.(12分)
20.解析 (1)证明:在菱形ABCD中,记AC,BD的交点为O,
则OA=OC=4,∵AD=5,∴OB=OD=3.
将△ABD折起后变成三棱锥A-BCD,在△ACD中,
AC2=AD2+CD2-2AD·CDcos∠ADC=25+25-2×5×5×=32.
在△AOC中,OA2+OC2=32=AC2,
∴∠AOC=90°,即AO⊥CO.
又AO⊥BO,BO∩CO=O,
∴AO⊥平面CBD.
又AO 平面ABD,
∴平面ABD⊥平面CBD.(5分)
(2)由(1)知OC,OD,OA两两互相垂直,故以O为原点,,,的方向分别为x轴、y轴、z轴正方向,建立如图所示的空间直角坐标系Oxyz,(7分)
则A(0,0,4),B(0,-3,0),C(4,0,0),D(0,3,0),M,(8分)
∴=,=(4,-3,0),=(4,0,-4).
设平面MCD的一个法向量为n=(x,y,z),
则即
取y=4,则x=3,z=9,∴n=(3,4,9).(10分)
设AC与平面MCD所成的角为θ,
则sin θ=|cos<,n>|===,
∴AC与平面MCD所成角的正弦值为. (12分)
21.解析 (1)证明:取PA的中点G,连接EG,DG.
因为PA∥BE,且PA=4,BE=2,所以BE∥AG,且BE=AG,
所以四边形BEGA为平行四边形,所以EG∥AB,且EG=AB.
因为四边形ABCD是正方形,所以CD∥AB,CD=AB,
所以EG∥CD,且EG=CD,
所以四边形CDGE为平行四边形,所以CE∥DG.
因为DG 平面PAD,CE 平面PAD,所以CE∥平面PAD.(4分)
(2)易得AB,AD,AP两两互相垂直,故以A为原点,,,的方向分别为x轴、y轴、z轴正方向,建立如图所示的空间直角坐标系,则B(4,0,0),C(4,4,0),E(4,0,2),P(0,0,4),D(0,4,0),(5分)
所以=(4,4,-4),=(4,0,-2),=(0,4,-4).
设平面PCE的一个法向量为m=(x,y,z),
则
令x=1,则y=1,z=2,所以m=(1,1,2).(8分)
假设存在点F(a,0,0)(0≤a≤4)满足题意,如图,连接EF,DF,DE,则=(4-a,0,2),=(4,-4,2).
设平面DEF的一个法向量为n=(x',y',z'),
则
令x'=2,则y'=,z'=a-4,
所以n=.(10分)
因为平面DEF⊥平面PCE,所以m·n=0,即2++2a-8=0,所以a=,故存在点F满足题意,此时=.(12分)
22.解析 (1)证明:取AD的中点H,连接EH,GH.
∵E,F,G,H分别是PD,PC,BC,AD的中点,
∴EF∥CD,GH∥CD,EH∥PA,
∴EF∥GH.
∴E,F,G,H四点共面.
∵PA∥EH,PA 平面EFG,EH 平面EFG,∴PA∥平面EFG.(4分)
(2)∵平面PDC ⊥平面ABCD,平面PDC∩平面ABCD=DC,AD⊥DC,∴AD⊥平面PDC.
以DA,DC所在直线分别为x轴,y轴,过点D且与平面ABCD垂直的直线为z轴,建立如图所示的空间直角坐标系Dxyz,
则G,E,F,
∴=(0,1,0),=,
易得平面EFD的一个法向量m=(1,0,0).
设平面EFG的一个法向量为n=(x,y,z),
∴即
令x=,则z=1,
∴n=(,0,1).(7分)
∴cos
∴
(3)易得P(0,1,),B(1,1,0),A(1,0,0),C(0,2,0),设Q(a,b,c),
则=(0,1,-),=(1,0,-),
=(a,b-1,c-)=λ=λ(1,0,-)=(λ,0,-λ),
∴Q(λ,1,-λ),=(λ-1,1,-λ).(10分)
∵PC⊥平面ADQ,∴PC⊥AQ,
∴·=1-(-λ)=0,解得λ=,满足题意.(12分)
