2.5 解直角三角形的应用 同步练习(含解析)
文档属性
| 名称 | 2.5 解直角三角形的应用 同步练习(含解析) |

|
|
| 格式 | docx | ||
| 文件大小 | 250.1KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-11-19 20:56:57 | ||
图片预览



文档简介
绝密★启用前
2.5解直角三角形的应用同步练习
青岛版初中数学九年级上册
一、选择题
同学们参加综合实践活动时,看到木工师傅用“三弧法”在板材边角处作直角,其作法是:如图.
作线段,分别以点,为圆心,长为半径作弧,两弧交于点;
以点为圆心,仍以长为半径作弧交的延长线于点;
连接,.
根据以上作图过程及所作图形,下列结论中错误的是
A. B.
C. D.
如图,两根竹竿和斜靠在墙上,量得,,则竹竿与的长度之比为
A.
B.
C.
D.
如图,一棵珍贵的树倾斜程度越来越厉害了.出于对它的保护,需要测量它的高度,现采取以下措施:在地面上选取一点,测得,米,,则这棵树的高约为参考数据:,,
A. 米 B. 米 C. 米 D. 米
如图,嘉淇一家驾车从地出发,沿着北偏东的方向行驶,到达地后沿着南偏东的方向行驶来到地,且地恰好位于地正东方向上,则下列说法正确的是
A. 地在地的北偏西方向上 B. 地在地的南偏西方向上
C. D.
如图,在综合实践活动中,小明在学校门口的点处测得树的顶端仰角为,同时测得米,则树的高单位:米为
A.
B.
C.
D.
如图所示,斜面的坡度与的比为,米,坡顶有旗杆,旗杆顶端点与点有一条彩带相连.若米,则旗杆的高度为
A. 米
B. 米
C. 米
D. 米
如图,一辆小车沿倾斜角为的斜坡向上行驶米,已知,则小车上升的高度是
A. 米 B. 米 C. 米 D. 米
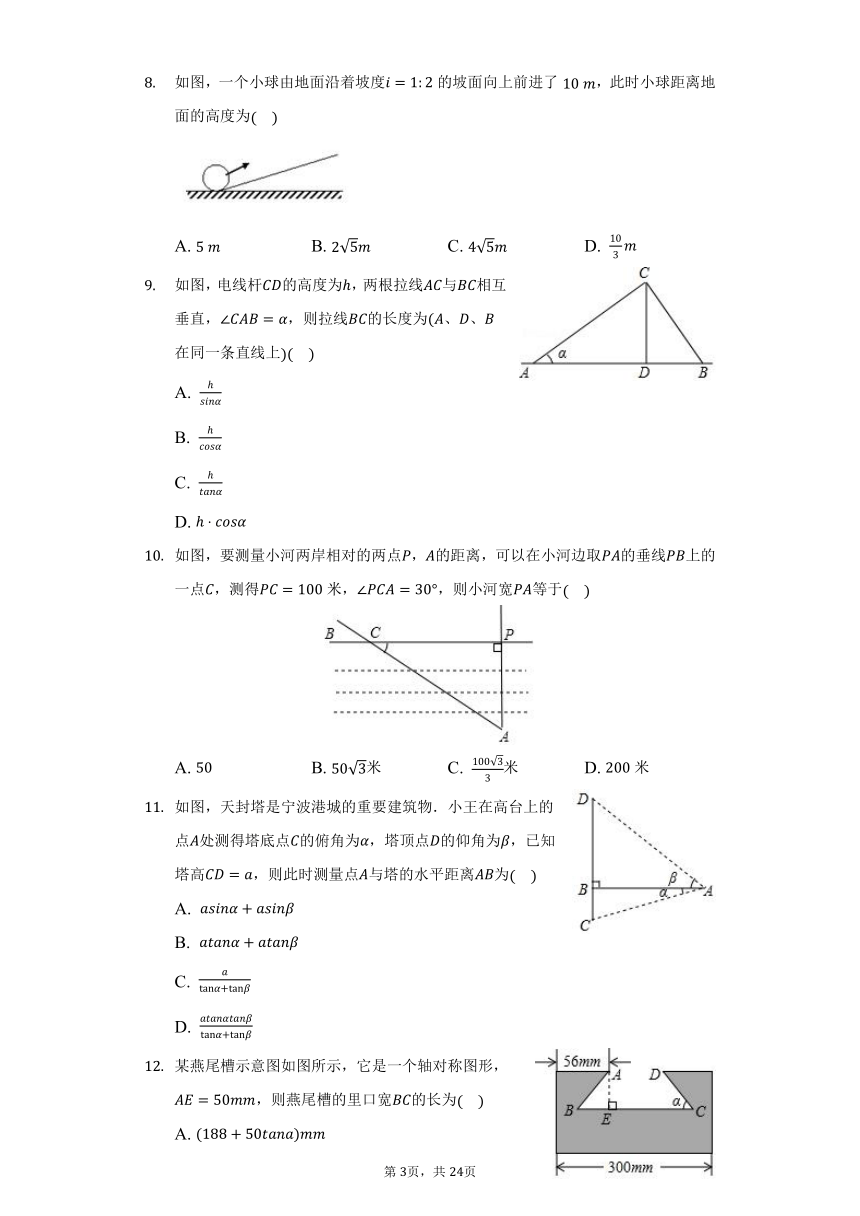
如图,一个小球由地面沿着坡度的坡面向上前进了,此时小球距离地面的高度为
A. B. C. D.
如图,电线杆的高度为,两根拉线与相互垂直,,则拉线的长度为、、在同一条直线上
A.
B.
C.
D.
如图,要测量小河两岸相对的两点,的距离,可以在小河边取的垂线上的一点,测得米,,则小河宽等于
A. B. 米 C. 米 D. 米
如图,天封塔是宁波港城的重要建筑物.小王在高台上的点处测得塔底点的俯角为,塔顶点的仰角为,已知塔高,则此时测量点与塔的水平距离为
A.
B.
C.
D.
某燕尾槽示意图如图所示,它是一个轴对称图形,,则燕尾槽的里口宽的长为
A.
B.
C.
D.
二、填空题
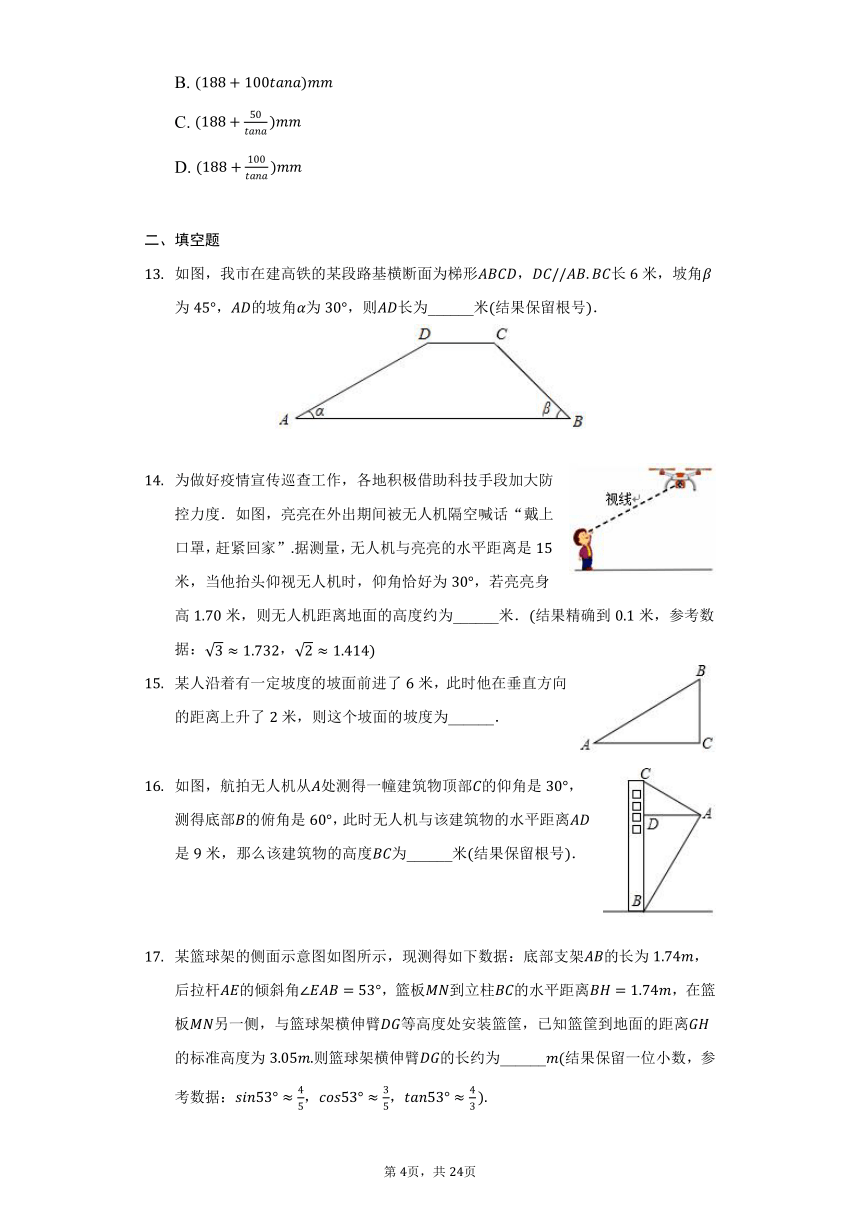
如图,我市在建高铁的某段路基横断面为梯形,长米,坡角为,的坡角为,则长为______米结果保留根号.
为做好疫情宣传巡查工作,各地积极借助科技手段加大防控力度.如图,亮亮在外出期间被无人机隔空喊话“戴上口罩,赶紧回家”据测量,无人机与亮亮的水平距离是米,当他抬头仰视无人机时,仰角恰好为,若亮亮身高米,则无人机距离地面的高度约为______米.结果精确到米,参考数据:,
某人沿着有一定坡度的坡面前进了米,此时他在垂直方向的距离上升了米,则这个坡面的坡度为______.
如图,航拍无人机从处测得一幢建筑物顶部的仰角是,测得底部的俯角是,此时无人机与该建筑物的水平距离是米,那么该建筑物的高度为______米结果保留根号.
某篮球架的侧面示意图如图所示,现测得如下数据:底部支架的长为,后拉杆的倾斜角,篮板到立柱的水平距离,在篮板另一侧,与篮球架横伸臂等高度处安装篮筐,已知篮筐到地面的距离的标准高度为则篮球架横伸臂的长约为______结果保留一位小数,参考数据:,,
三、解答题
自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多,为方便群众步行健身,某地政府决定对一段如图所示的坡路进行改造.如图所示,改造前的斜坡米,坡度为:;将斜坡的高度降低米后,斜坡改造为斜坡,其坡度为:求斜坡的长.结果保留根号
如图,某小区号楼与号楼隔河相望,李明家住在号楼,他很想知道号楼的高度,于是他做了一些测量,他先在点测得点的仰角为,然后到米高的楼顶处,测得点的仰角为,请你帮助李明计算号楼的高度.
为加快城乡对接,建设全域美丽乡村,某地区对、两地间的公路进行改建.如图,、两地之间有一座山,汽车原来从地到地需途经地沿折线行驶,现开通隧道后,汽车可直接沿直线行驶.已知千米,,.
开通隧道前,汽车从地到地大约要走多少千米?
开通隧道后,汽车从地到地大约可以少走多少千米?结果精确到千米参考数据:,
如图,自卸车车厢的一个侧面是矩形,米,米,车厢底部距离地面米.卸货时,车厢倾斜的角度,问此时车厢的最高点距离地面多少米?精确到
如图,和两幢楼地面距离为米,楼高米,从楼的顶部点测得楼的顶部点的仰角为.
求的大小;
求楼的高度结果保留根号.
楼房后有一假山,其坡度为:,山坡坡面上点处有一休息亭,测得假山坡脚与楼房水平距离米,与亭子距离米,小丽从楼房顶测得点的俯角为,求楼房的高.注:坡度是指坡面的铅直高度与水平宽度的比
如图,海岛在海岛的北偏东方向,且与海岛相距海里,一艘渔船从海岛出发,以海里时的速度沿北偏东方向航行,同时一艘快艇从海岛出发,向正东方向航行.小时后,快艇到达处,此时渔船恰好到达快艇正北方向的处.
求的度数;
求快艇的速度及,之间的距离.
参考数据:,,,
某海域有、两个港口,港口在港口北偏西方向上,距港口海里,有一艘船从港口出发,沿东北方向行驶一段距离后,到达位于港口南偏东方向的处,求:
的度数;
此时刻船与港口之间的距离的长结果保留根号.
答案和解析
1.【答案】
【解析】解:由作法得,故B正确;
点在以为直径的圆上,
,故A正确;
点是的外心,
在中,,
,,
,故C正确;,故D错误,
故选:.
由作法得,根据圆周角定理得到,点是的外心,根据三角函数的定义计算出,则,利用特殊角的三角函数值即可得到结论.
本题考查了解直角三角形,三角形的外接圆与外心:三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.也考查了圆周角定理和解直角三角形.
2.【答案】
【解析】
【试题解析】
【分析】
本题考查解直角三角形的应用、锐角三角函数等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.
在两个直角三角形中,分别求出、即可解决问题.
【解答】
解:在中,,
在中,,
::,
故选:.
3.【答案】
【解析】
【分析】
本题考查解直角三角形的应用,勾股定理的应用等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
如图,作于设,构建方程即可解决问题.
【解答】
解:如图,作于.
,,
设,
,
,
,
,
,
故选:.
4.【答案】
【解析】解:如图所示:
由题意可知,,,
,即在处的北偏西,故A错误;
,
,
即在处的北偏西,故B错误;
,
即公路和的夹角是,故C错误.
,
,
,故D正确;
故选:.
根据平行线的性质及方向角的概念分别解答即可.
本题考查的是解直角三角形方向角问题,熟练掌握方向角的概念是解题的关键.
5.【答案】
【解析】
【分析】
本题考查了解直角三角形的应用仰角俯角问题.
解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,通过解直角可以求得的长度.
【解答】
解:如图,在直角中,,,,
,
则.
故选:.
6.【答案】
【解析】
【分析】
本题考查了解直角三角形的应用--坡度坡角问题,找到合适的直角三角形,熟练运用勾股定理是解题的关键.设,则,根据勾股定理求出的长,从而求出、的长,然后根据勾股定理求出的长,即可求出的长.
【解答】
解:设米,则米,
由勾股定理可得,米,
米,
,
米,
米,
米,
在中,米,
米.
故答案为.
7.【答案】
【解析】解:如图,作,
,
,
,
小车上升的高度是.
故选A.
在中,先求出,再利用勾股定理求出即可.
此题主要考查解直角三角形,锐角三角函数,勾股定理等知识,解题的关键是学会构造直角三角形解决问题,属于中考常考题型.
8.【答案】
【解析】解:米,.
设,,
由勾股定理得,,即,解得,
,米.
故选:.
可利用勾股定理及所给的比值得到所求的线段长.
本题主要考查了解直角三角形的应用坡度坡角问题,能从实际问题中整理出直角三角形是解答本题的关键.
9.【答案】
【解析】
【分析】
本题主要考查解直角三角形的应用,熟练掌握同角的余角相等和三角函数的定义是解题的关键根据同角的余角相等得,由可知
【解答】
解:,,
,,
,
在中,,
,
故选B.
10.【答案】
【解析】解:,米,,
小河宽米.
故选:.
根据正切函数可求小河宽的长度.
考查了解直角三角形的应用,解直角三角形的一般过程是:将实际问题抽象为数学问题画出平面图形,构造出直角三角形转化为解直角三角形问题根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.
11.【答案】
【解析】解:设,
在中有,,
在中有,,
又,
,
,
即,
故选:.
利用直角三角形的边角关系,用含有的代数式表示、,再根据,列方程求解即可.
本题考查直角三角形的应用,掌握直角三角形的边角关系是正确解答的前提.
12.【答案】
【解析】解:如图,作于点,于点,
燕尾槽是一个轴对称图形,
,,
,
中,,
同理可得,
.
故选:.
作等腰梯形的两条高,将梯形问题转换成造直角三角形和矩形问题,然后在直角三角形中利用正切定义求得和相关的两条线段,进而求出题目的结果.
本题考查轴对称图形的性质、矩形的判定与性质、正切等知识,是重要考点,难度一般,掌握相关知识是解题关键.
13.【答案】
【解析】
【分析】
本题考查解直角三角形的应用坡度坡角问题,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
过点作于,过点作于首先证明,解直角三角形求出,再根据直角三角形度角的性质即可解决问题.
【解答】
解:过点作于,过点作于.
,,,
,
在中,米,
米,
在中,,,
米,
故答案为.
14.【答案】
【解析】解:如图,
根据题意可知:
,,
过点作于点,
所以四边形是矩形,
,
,
在中,,
,
即,
解得,
米.
答:无人机距离地面的高度约为米.
根据题意可得,,,过点作于点,所以四边形是矩形,再根据锐角三角函数即可求出的长,进而可求出的长.
本题考查了解直角三角形的应用仰角俯角问题,解决本题的关键是掌握仰角俯角定义.
15.【答案】
【解析】解:由题意可得:,,
则在直角中,
,
故这个坡面的坡度为:.
故答案为:.
直接利用勾股定理得出的长,再利用坡角的定义得出答案.
此题主要考查了坡角的定义,正确把握坡角的定义是解题关键.
16.【答案】
【解析】解:根据题意可知:
在中,,,
,
在中,,,
,
米.
答;该建筑物的高度为米.
故答案为:.
根据题意可得在中,,,在中,,,再根据特殊角三角函数即可分别求出和的长,进而可得该建筑物的高度.
本题考查了解直角三角形的应用仰角俯角问题,解决本题的关键是掌握仰角俯角定义.
17.【答案】
【解析】解:作于.
四边形是矩形,
,
在中.,
,
故答案为.
作于得到矩形,求出即可解决问题;
本题考查解直角三角形的应用,锐角三角函数、矩形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
18.【答案】解:,,坡度为:,
,
,
,
,
,
,斜坡的坡度为:,
,
即,
解得,,
米,
答:斜坡的长是米.
【解析】根据题意和锐角三角函数可以求得的长,进而得到的长,再根据锐角三角函数可以得到的长,最后用勾股定理即可求得的长.
本题考查解直角三角形的应用坡度坡角问题,解答本题的关键是明确题意,利用锐角三角函数解答.
19.【答案】解:作,
,,
,
,
.
答:乙建筑物的高度为.
【解析】作,用可以分别表示,的长,根据,即可求得长,即可解题.
本题考查了直角三角形中三角函数的应用,考查了特殊角的三角函数值,本题中求的的长是解题的关键.
20.【答案】解:过点作的垂线,垂足为,
,,千米,
千米,
千米,
千米,
答:开通隧道前,汽车从地到地要走千米;
,千米,
千米,
,千米,
千米,
千米,
汽车从地到地比原来少走多少路程为:千米.
答:汽车从地到地比原来少走的路程为千米.
【解析】过点作的垂线,垂足为,在直角中,解直角三角形求出,进而解答即可;
在直角中,解直角三角形求出,再求出,进而求出汽车从地到地比原来少走多少路程.
本题考查了勾股定理的运用以及解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.
21.【答案】解:如图,过作于点,延长交的延长线于点,
,,
,
米,
在中,,
那么,
在中,,
点距离地面为.
【解析】要算出点距离地面的距离,只需算出点距离车厢的距离加上米即可.如下图,过作于点,延长交的延长线于点,在中,根据已知条件可以求出,然后可以求出,也就求出了,最后可以求出,加上就是点距离地面.
解决本题的难点是构造所求线段所在的直角三角形,然后利用三角函数的定义得到关于所求线段的关系求出其结果.
22.【答案】解:过作于点,
则米,米,
在中,,
则,
则;
在中,米,
米.
【解析】过作于点,可得米,米,在直角三角形中,利用锐角三角函数的定义求出,进一步求得的大小;
利用等腰直角三角形的性质求出的长,由求出的长即可.
此题考查了解直角三角形的应用仰角俯角问题,熟练掌握锐角三角函数的定义是解本题的关键.
23.【答案】解:过点作的延长线于,于点,
在中,
,
,
米,米,
米,米,
在中,,
米,
米.
答:楼房的高为米.
【解析】过点作的延长线于,于点,根据米,坡度为:,分别求出、的长度,在中求出,继而可得楼房的高.
本题考查了解直角三角形的应用,涉及仰角俯角及坡度坡角的知识,构造直角三角形是解题关键.
24.【答案】解:过点作于点,作于点,
由题意得,,,
,
,
而,
;
海里,
在中,,
海里,
海里,
在中,,,
海里,
,
,,,
,
四边形为矩形,
,,
,
,
设快艇的速度为海里小时,则海里小时.
答:快艇的速度为海里小时,,之间的距离为海里.
【解析】过点作于点,作于点,由平行线的性质得出,求出,则可得出答案;
在中,解直角三角形求出,,在中,解直角三角形求出,,证明四边形为矩形,得出,,求出的长,则可得出答案.
本题考查的是解直角三角形的应用,掌握方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合是解题的关键.
25.【答案】解:如图,,,
,
又,
,
又,
;
如图,作于.
在中,
,海里,
海里,
在中,,海里,
海里,
海里,
答:该船与港口之间的距离的长为海里.
【解析】本题考查的是解直角三角形的应用方向角问题,平行线的性质,三角形内角和定理,构造直角三角形,利用三角函数求出线段与的长度是解题的关键.
由平行线的性质以及方向角的定义得出,,那么,又根据方向角的定义得出,利用三角形内角和定理求出;
作交于点,解,得出,解,得出,进而得出.
第8页,共24页
第9页,共24页
2.5解直角三角形的应用同步练习
青岛版初中数学九年级上册
一、选择题
同学们参加综合实践活动时,看到木工师傅用“三弧法”在板材边角处作直角,其作法是:如图.
作线段,分别以点,为圆心,长为半径作弧,两弧交于点;
以点为圆心,仍以长为半径作弧交的延长线于点;
连接,.
根据以上作图过程及所作图形,下列结论中错误的是
A. B.
C. D.
如图,两根竹竿和斜靠在墙上,量得,,则竹竿与的长度之比为
A.
B.
C.
D.
如图,一棵珍贵的树倾斜程度越来越厉害了.出于对它的保护,需要测量它的高度,现采取以下措施:在地面上选取一点,测得,米,,则这棵树的高约为参考数据:,,
A. 米 B. 米 C. 米 D. 米
如图,嘉淇一家驾车从地出发,沿着北偏东的方向行驶,到达地后沿着南偏东的方向行驶来到地,且地恰好位于地正东方向上,则下列说法正确的是
A. 地在地的北偏西方向上 B. 地在地的南偏西方向上
C. D.
如图,在综合实践活动中,小明在学校门口的点处测得树的顶端仰角为,同时测得米,则树的高单位:米为
A.
B.
C.
D.
如图所示,斜面的坡度与的比为,米,坡顶有旗杆,旗杆顶端点与点有一条彩带相连.若米,则旗杆的高度为
A. 米
B. 米
C. 米
D. 米
如图,一辆小车沿倾斜角为的斜坡向上行驶米,已知,则小车上升的高度是
A. 米 B. 米 C. 米 D. 米
如图,一个小球由地面沿着坡度的坡面向上前进了,此时小球距离地面的高度为
A. B. C. D.
如图,电线杆的高度为,两根拉线与相互垂直,,则拉线的长度为、、在同一条直线上
A.
B.
C.
D.
如图,要测量小河两岸相对的两点,的距离,可以在小河边取的垂线上的一点,测得米,,则小河宽等于
A. B. 米 C. 米 D. 米
如图,天封塔是宁波港城的重要建筑物.小王在高台上的点处测得塔底点的俯角为,塔顶点的仰角为,已知塔高,则此时测量点与塔的水平距离为
A.
B.
C.
D.
某燕尾槽示意图如图所示,它是一个轴对称图形,,则燕尾槽的里口宽的长为
A.
B.
C.
D.
二、填空题
如图,我市在建高铁的某段路基横断面为梯形,长米,坡角为,的坡角为,则长为______米结果保留根号.
为做好疫情宣传巡查工作,各地积极借助科技手段加大防控力度.如图,亮亮在外出期间被无人机隔空喊话“戴上口罩,赶紧回家”据测量,无人机与亮亮的水平距离是米,当他抬头仰视无人机时,仰角恰好为,若亮亮身高米,则无人机距离地面的高度约为______米.结果精确到米,参考数据:,
某人沿着有一定坡度的坡面前进了米,此时他在垂直方向的距离上升了米,则这个坡面的坡度为______.
如图,航拍无人机从处测得一幢建筑物顶部的仰角是,测得底部的俯角是,此时无人机与该建筑物的水平距离是米,那么该建筑物的高度为______米结果保留根号.
某篮球架的侧面示意图如图所示,现测得如下数据:底部支架的长为,后拉杆的倾斜角,篮板到立柱的水平距离,在篮板另一侧,与篮球架横伸臂等高度处安装篮筐,已知篮筐到地面的距离的标准高度为则篮球架横伸臂的长约为______结果保留一位小数,参考数据:,,
三、解答题
自开展“全民健身运动”以来,喜欢户外步行健身的人越来越多,为方便群众步行健身,某地政府决定对一段如图所示的坡路进行改造.如图所示,改造前的斜坡米,坡度为:;将斜坡的高度降低米后,斜坡改造为斜坡,其坡度为:求斜坡的长.结果保留根号
如图,某小区号楼与号楼隔河相望,李明家住在号楼,他很想知道号楼的高度,于是他做了一些测量,他先在点测得点的仰角为,然后到米高的楼顶处,测得点的仰角为,请你帮助李明计算号楼的高度.
为加快城乡对接,建设全域美丽乡村,某地区对、两地间的公路进行改建.如图,、两地之间有一座山,汽车原来从地到地需途经地沿折线行驶,现开通隧道后,汽车可直接沿直线行驶.已知千米,,.
开通隧道前,汽车从地到地大约要走多少千米?
开通隧道后,汽车从地到地大约可以少走多少千米?结果精确到千米参考数据:,
如图,自卸车车厢的一个侧面是矩形,米,米,车厢底部距离地面米.卸货时,车厢倾斜的角度,问此时车厢的最高点距离地面多少米?精确到
如图,和两幢楼地面距离为米,楼高米,从楼的顶部点测得楼的顶部点的仰角为.
求的大小;
求楼的高度结果保留根号.
楼房后有一假山,其坡度为:,山坡坡面上点处有一休息亭,测得假山坡脚与楼房水平距离米,与亭子距离米,小丽从楼房顶测得点的俯角为,求楼房的高.注:坡度是指坡面的铅直高度与水平宽度的比
如图,海岛在海岛的北偏东方向,且与海岛相距海里,一艘渔船从海岛出发,以海里时的速度沿北偏东方向航行,同时一艘快艇从海岛出发,向正东方向航行.小时后,快艇到达处,此时渔船恰好到达快艇正北方向的处.
求的度数;
求快艇的速度及,之间的距离.
参考数据:,,,
某海域有、两个港口,港口在港口北偏西方向上,距港口海里,有一艘船从港口出发,沿东北方向行驶一段距离后,到达位于港口南偏东方向的处,求:
的度数;
此时刻船与港口之间的距离的长结果保留根号.
答案和解析
1.【答案】
【解析】解:由作法得,故B正确;
点在以为直径的圆上,
,故A正确;
点是的外心,
在中,,
,,
,故C正确;,故D错误,
故选:.
由作法得,根据圆周角定理得到,点是的外心,根据三角函数的定义计算出,则,利用特殊角的三角函数值即可得到结论.
本题考查了解直角三角形,三角形的外接圆与外心:三角形外接圆的圆心是三角形三条边垂直平分线的交点,叫做三角形的外心.也考查了圆周角定理和解直角三角形.
2.【答案】
【解析】
【试题解析】
【分析】
本题考查解直角三角形的应用、锐角三角函数等知识,解题的关键是学会利用参数解决问题,属于中考常考题型.
在两个直角三角形中,分别求出、即可解决问题.
【解答】
解:在中,,
在中,,
::,
故选:.
3.【答案】
【解析】
【分析】
本题考查解直角三角形的应用,勾股定理的应用等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题,属于中考常考题型.
如图,作于设,构建方程即可解决问题.
【解答】
解:如图,作于.
,,
设,
,
,
,
,
,
故选:.
4.【答案】
【解析】解:如图所示:
由题意可知,,,
,即在处的北偏西,故A错误;
,
,
即在处的北偏西,故B错误;
,
即公路和的夹角是,故C错误.
,
,
,故D正确;
故选:.
根据平行线的性质及方向角的概念分别解答即可.
本题考查的是解直角三角形方向角问题,熟练掌握方向角的概念是解题的关键.
5.【答案】
【解析】
【分析】
本题考查了解直角三角形的应用仰角俯角问题.
解决此类问题要了解角之间的关系,找到与已知和未知相关联的直角三角形,通过解直角可以求得的长度.
【解答】
解:如图,在直角中,,,,
,
则.
故选:.
6.【答案】
【解析】
【分析】
本题考查了解直角三角形的应用--坡度坡角问题,找到合适的直角三角形,熟练运用勾股定理是解题的关键.设,则,根据勾股定理求出的长,从而求出、的长,然后根据勾股定理求出的长,即可求出的长.
【解答】
解:设米,则米,
由勾股定理可得,米,
米,
,
米,
米,
米,
在中,米,
米.
故答案为.
7.【答案】
【解析】解:如图,作,
,
,
,
小车上升的高度是.
故选A.
在中,先求出,再利用勾股定理求出即可.
此题主要考查解直角三角形,锐角三角函数,勾股定理等知识,解题的关键是学会构造直角三角形解决问题,属于中考常考题型.
8.【答案】
【解析】解:米,.
设,,
由勾股定理得,,即,解得,
,米.
故选:.
可利用勾股定理及所给的比值得到所求的线段长.
本题主要考查了解直角三角形的应用坡度坡角问题,能从实际问题中整理出直角三角形是解答本题的关键.
9.【答案】
【解析】
【分析】
本题主要考查解直角三角形的应用,熟练掌握同角的余角相等和三角函数的定义是解题的关键根据同角的余角相等得,由可知
【解答】
解:,,
,,
,
在中,,
,
故选B.
10.【答案】
【解析】解:,米,,
小河宽米.
故选:.
根据正切函数可求小河宽的长度.
考查了解直角三角形的应用,解直角三角形的一般过程是:将实际问题抽象为数学问题画出平面图形,构造出直角三角形转化为解直角三角形问题根据题目已知特点选用适当锐角三角函数或边角关系去解直角三角形,得到数学问题的答案,再转化得到实际问题的答案.
11.【答案】
【解析】解:设,
在中有,,
在中有,,
又,
,
,
即,
故选:.
利用直角三角形的边角关系,用含有的代数式表示、,再根据,列方程求解即可.
本题考查直角三角形的应用,掌握直角三角形的边角关系是正确解答的前提.
12.【答案】
【解析】解:如图,作于点,于点,
燕尾槽是一个轴对称图形,
,,
,
中,,
同理可得,
.
故选:.
作等腰梯形的两条高,将梯形问题转换成造直角三角形和矩形问题,然后在直角三角形中利用正切定义求得和相关的两条线段,进而求出题目的结果.
本题考查轴对称图形的性质、矩形的判定与性质、正切等知识,是重要考点,难度一般,掌握相关知识是解题关键.
13.【答案】
【解析】
【分析】
本题考查解直角三角形的应用坡度坡角问题,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
过点作于,过点作于首先证明,解直角三角形求出,再根据直角三角形度角的性质即可解决问题.
【解答】
解:过点作于,过点作于.
,,,
,
在中,米,
米,
在中,,,
米,
故答案为.
14.【答案】
【解析】解:如图,
根据题意可知:
,,
过点作于点,
所以四边形是矩形,
,
,
在中,,
,
即,
解得,
米.
答:无人机距离地面的高度约为米.
根据题意可得,,,过点作于点,所以四边形是矩形,再根据锐角三角函数即可求出的长,进而可求出的长.
本题考查了解直角三角形的应用仰角俯角问题,解决本题的关键是掌握仰角俯角定义.
15.【答案】
【解析】解:由题意可得:,,
则在直角中,
,
故这个坡面的坡度为:.
故答案为:.
直接利用勾股定理得出的长,再利用坡角的定义得出答案.
此题主要考查了坡角的定义,正确把握坡角的定义是解题关键.
16.【答案】
【解析】解:根据题意可知:
在中,,,
,
在中,,,
,
米.
答;该建筑物的高度为米.
故答案为:.
根据题意可得在中,,,在中,,,再根据特殊角三角函数即可分别求出和的长,进而可得该建筑物的高度.
本题考查了解直角三角形的应用仰角俯角问题,解决本题的关键是掌握仰角俯角定义.
17.【答案】
【解析】解:作于.
四边形是矩形,
,
在中.,
,
故答案为.
作于得到矩形,求出即可解决问题;
本题考查解直角三角形的应用,锐角三角函数、矩形的判定和性质等知识,解题的关键是学会添加常用辅助线,构造直角三角形解决问题.
18.【答案】解:,,坡度为:,
,
,
,
,
,
,斜坡的坡度为:,
,
即,
解得,,
米,
答:斜坡的长是米.
【解析】根据题意和锐角三角函数可以求得的长,进而得到的长,再根据锐角三角函数可以得到的长,最后用勾股定理即可求得的长.
本题考查解直角三角形的应用坡度坡角问题,解答本题的关键是明确题意,利用锐角三角函数解答.
19.【答案】解:作,
,,
,
,
.
答:乙建筑物的高度为.
【解析】作,用可以分别表示,的长,根据,即可求得长,即可解题.
本题考查了直角三角形中三角函数的应用,考查了特殊角的三角函数值,本题中求的的长是解题的关键.
20.【答案】解:过点作的垂线,垂足为,
,,千米,
千米,
千米,
千米,
答:开通隧道前,汽车从地到地要走千米;
,千米,
千米,
,千米,
千米,
千米,
汽车从地到地比原来少走多少路程为:千米.
答:汽车从地到地比原来少走的路程为千米.
【解析】过点作的垂线,垂足为,在直角中,解直角三角形求出,进而解答即可;
在直角中,解直角三角形求出,再求出,进而求出汽车从地到地比原来少走多少路程.
本题考查了勾股定理的运用以及解一般三角形,求三角形的边或高的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.
21.【答案】解:如图,过作于点,延长交的延长线于点,
,,
,
米,
在中,,
那么,
在中,,
点距离地面为.
【解析】要算出点距离地面的距离,只需算出点距离车厢的距离加上米即可.如下图,过作于点,延长交的延长线于点,在中,根据已知条件可以求出,然后可以求出,也就求出了,最后可以求出,加上就是点距离地面.
解决本题的难点是构造所求线段所在的直角三角形,然后利用三角函数的定义得到关于所求线段的关系求出其结果.
22.【答案】解:过作于点,
则米,米,
在中,,
则,
则;
在中,米,
米.
【解析】过作于点,可得米,米,在直角三角形中,利用锐角三角函数的定义求出,进一步求得的大小;
利用等腰直角三角形的性质求出的长,由求出的长即可.
此题考查了解直角三角形的应用仰角俯角问题,熟练掌握锐角三角函数的定义是解本题的关键.
23.【答案】解:过点作的延长线于,于点,
在中,
,
,
米,米,
米,米,
在中,,
米,
米.
答:楼房的高为米.
【解析】过点作的延长线于,于点,根据米,坡度为:,分别求出、的长度,在中求出,继而可得楼房的高.
本题考查了解直角三角形的应用,涉及仰角俯角及坡度坡角的知识,构造直角三角形是解题关键.
24.【答案】解:过点作于点,作于点,
由题意得,,,
,
,
而,
;
海里,
在中,,
海里,
海里,
在中,,,
海里,
,
,,,
,
四边形为矩形,
,,
,
,
设快艇的速度为海里小时,则海里小时.
答:快艇的速度为海里小时,,之间的距离为海里.
【解析】过点作于点,作于点,由平行线的性质得出,求出,则可得出答案;
在中,解直角三角形求出,,在中,解直角三角形求出,,证明四边形为矩形,得出,,求出的长,则可得出答案.
本题考查的是解直角三角形的应用,掌握方向角问题,结合航海中的实际问题,将解直角三角形的相关知识有机结合是解题的关键.
25.【答案】解:如图,,,
,
又,
,
又,
;
如图,作于.
在中,
,海里,
海里,
在中,,海里,
海里,
海里,
答:该船与港口之间的距离的长为海里.
【解析】本题考查的是解直角三角形的应用方向角问题,平行线的性质,三角形内角和定理,构造直角三角形,利用三角函数求出线段与的长度是解题的关键.
由平行线的性质以及方向角的定义得出,,那么,又根据方向角的定义得出,利用三角形内角和定理求出;
作交于点,解,得出,解,得出,进而得出.
第8页,共24页
第9页,共24页
同课章节目录
- 第1章 图形的相似
- 1.1 相似多边形
- 1.2 怎样判定三角形相似
- 1.3 相似三角形的性质
- 1.4 图形的位似
- 第2章 解直角三角形
- 2.1 锐角三角比
- 2.2 30°,45°,60°角的三角比
- 2.3 用计算器求锐角三角比
- 2.4 解直角三角形
- 2.5 解直角三角形的应用
- 第3章 对圆的进一步认识
- 3.1 圆的对称性
- 3.2 确定圆的条件
- 3.3 圆周角
- 3.4 直线与圆的位置关系
- 3.5 三角形的内切圆
- 3.6 弧长及扇形面积的计算
- 3.7 正多边形与圆
- 课题学习 图形变换与图案设计
- 第4章 一元二次方程
- 4.1 一元二次方程
- 4.2 用配方法解一元二次方程
- 4.3 用公式法解一元二次方程
- 4.4 用因式分解法解一元二次方程
- 4.5 一元二次方程的应用
- 4.6 一元二次方程根与系数的关系
