第12章 专题训练(二)证明三角形全等的基本模型 习题课件
文档属性
| 名称 | 第12章 专题训练(二)证明三角形全等的基本模型 习题课件 |  | |
| 格式 | pptx | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:17:17 | ||
图片预览






文档简介
(共28张PPT)
类型1平移模型
模型特征:其中有一个图形可以看作另一个图形
平移而得,其常见的图形有
1.(南充)如图,点O是线段AB的中点,OD∥
BC且OD=BC.
(1)求证:△AOD≌△OBC;
(2)若∠ADO=35°,求∠DOC的度数
(1)证明:∵点O是线段AB的
中点,∴AO=BO
OD∥BC,∴∠AOD=∠OBC
在△AOD与△OBC中,
Ao= BO
∠AOD=∠OBC,∴△AOD≌△OBC(SAS)
OD=BC
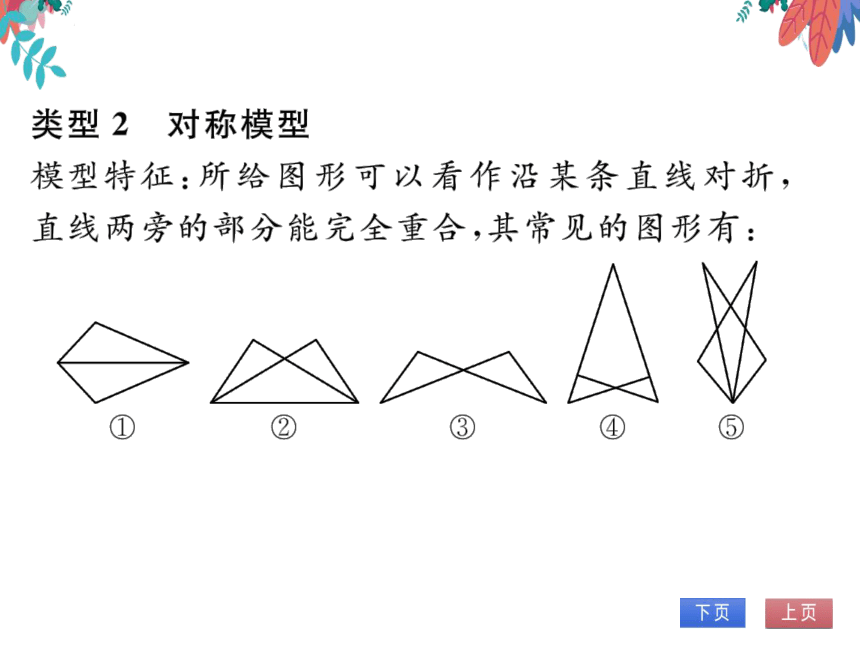
类型2对称模型
模型特征:所给图形可以看作沿某条直线对折,
直线两旁的部分能完全重合,其常见的图形有
如图,在四边形ABCD中,AB=AD,CB
CD,过点C作CM⊥AB于点M,CN⊥AD于
点N.求证:CM=CN
证明:如图,连接AC
在△ABC和△ADC中,
AB=AD
A
AC=AC
CB=CD
B
M
△ABC≌△ADC(SSS)
∠DAC=∠BAC
又∵CM⊥AB,CN⊥AD,
∴∠AMC=∠ANC=90
在△AMC和△ANC中
BAC=∠DAC,
∠AMC=∠ANC,∴△AMC≌△ANC.
AC=AC
CM=CN
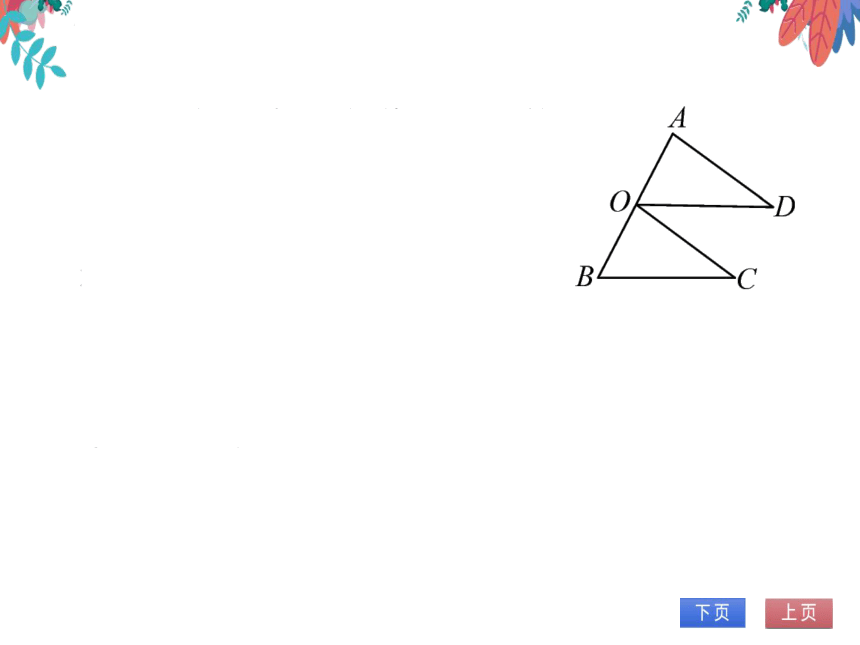
3.某产品的商标如图所示,O是线段AC,DB的交
点,且AC=BD,AB=CD,小华认为图中的两个
三角形全等,他的思考过程是:∵AC=DB,
∠AOB
DOC,AB=DC,∴AABO
DCO
你认为小华的思考过程正确吗 如果正确,指
出他用的是判别三角形全等的哪个条件;如果
不正确,写出你的思考过程
解:小华的思考过程不正A
确,因为AC和BD不是这
两个三角形的边
正确的解答是:如图,连接
BC,在△ABC和△DCB中
AB=DC
AC=DB,∴△ABC≌△DCB(SSS)
BC=CB
∠A=∠D.
∠AOB=∠DOC
在△AOB和△DOC中,∠A=∠D,
AB= DC
△AOB≌△DOC(AAS)
类型3旋转模型
模型特征:此类题目的某个图形可以看作由另
个图形绕某点旋转得到的,其常见的图形有
4.复习“全等三角形”的知识时,老师布置了一道
作业题:“如图①,在△ABC中,AB=AC,P是
△ABC内任意一点,将AP绕点A顺时针旋
转至AQ,使∠QAP=∠BAC,连接BQ,CP,
则BQ=CP.”小亮是个爱动脑筋的同学,他通
过对图①的分析,证明了△ABQ≌△ACP,从
而证得BQ=CP.之后,他将点P移到等腰
△ABC外,原题中其他条件不变,发现“BQ
CP”仍然成立,请你就图②给出证明
类型1平移模型
模型特征:其中有一个图形可以看作另一个图形
平移而得,其常见的图形有
1.(南充)如图,点O是线段AB的中点,OD∥
BC且OD=BC.
(1)求证:△AOD≌△OBC;
(2)若∠ADO=35°,求∠DOC的度数
(1)证明:∵点O是线段AB的
中点,∴AO=BO
OD∥BC,∴∠AOD=∠OBC
在△AOD与△OBC中,
Ao= BO
∠AOD=∠OBC,∴△AOD≌△OBC(SAS)
OD=BC
类型2对称模型
模型特征:所给图形可以看作沿某条直线对折,
直线两旁的部分能完全重合,其常见的图形有
如图,在四边形ABCD中,AB=AD,CB
CD,过点C作CM⊥AB于点M,CN⊥AD于
点N.求证:CM=CN
证明:如图,连接AC
在△ABC和△ADC中,
AB=AD
A
AC=AC
CB=CD
B
M
△ABC≌△ADC(SSS)
∠DAC=∠BAC
又∵CM⊥AB,CN⊥AD,
∴∠AMC=∠ANC=90
在△AMC和△ANC中
BAC=∠DAC,
∠AMC=∠ANC,∴△AMC≌△ANC.
AC=AC
CM=CN
3.某产品的商标如图所示,O是线段AC,DB的交
点,且AC=BD,AB=CD,小华认为图中的两个
三角形全等,他的思考过程是:∵AC=DB,
∠AOB
DOC,AB=DC,∴AABO
DCO
你认为小华的思考过程正确吗 如果正确,指
出他用的是判别三角形全等的哪个条件;如果
不正确,写出你的思考过程
解:小华的思考过程不正A
确,因为AC和BD不是这
两个三角形的边
正确的解答是:如图,连接
BC,在△ABC和△DCB中
AB=DC
AC=DB,∴△ABC≌△DCB(SSS)
BC=CB
∠A=∠D.
∠AOB=∠DOC
在△AOB和△DOC中,∠A=∠D,
AB= DC
△AOB≌△DOC(AAS)
类型3旋转模型
模型特征:此类题目的某个图形可以看作由另
个图形绕某点旋转得到的,其常见的图形有
4.复习“全等三角形”的知识时,老师布置了一道
作业题:“如图①,在△ABC中,AB=AC,P是
△ABC内任意一点,将AP绕点A顺时针旋
转至AQ,使∠QAP=∠BAC,连接BQ,CP,
则BQ=CP.”小亮是个爱动脑筋的同学,他通
过对图①的分析,证明了△ABQ≌△ACP,从
而证得BQ=CP.之后,他将点P移到等腰
△ABC外,原题中其他条件不变,发现“BQ
CP”仍然成立,请你就图②给出证明
