第15章 重难点突破 习题课件
图片预览








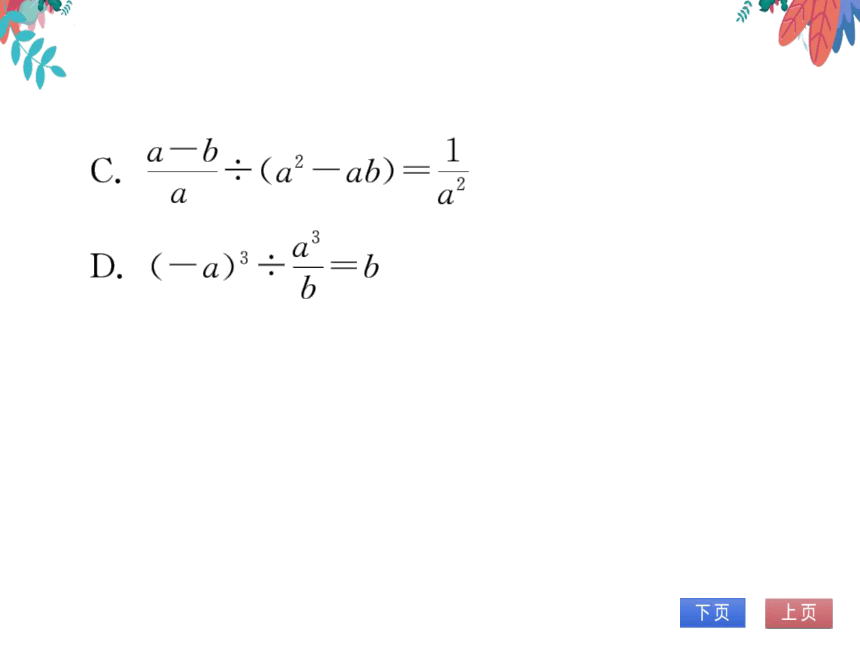
文档简介
(共27张PPT)
标题截图放置居中位置
考点1分式的相关概念及性质
1.若分式
有意义,则x的取值范围是(D)
A
D.x≠-2
2.若分式
的值为零,则x的值是(A
D.10
3.下列运算中,正确的是
A
n212+m
2ab
ab
b-b
b
b
b
4.分式
c m
ya2-b,x+中,最简分式有
A.1个B.2个C.3个D.4个
考点2负整数指数幂与科学记数法
5.(硚口区)下列等式正确的是
A.(-3)
B.4
4
0.0000618=6.18×10
D.20-1=1
6.新型冠状病毒的直径是100nm(1nm
10m),则新型冠状病毒的直径用科学记数
法表示是
A.10-8m
B.10-2nm
C.10
D.10
计算:(2m2n-3)=2·(
解:原式=2-2m4n
36
2n2
4+3-(-6)6+6-2
2214
2510
2n2
考点3分式的运算及化简求值
8.下列各式计算错误的是
Bab lo.r
4r
21b
14x
xy. 3xy 4y
y
3.3
b
ab)
C
b
4a+4
9.当a=2020时,计算
4
的结果是
(B)
A.2019
B.2020
D.2021
2020
10.(朝阳)先化简,再求值:
2-4
2a+6
Q,其中
212
2
+3
2(a-2)2
解:原式
a+2(a+2)(a-2)2(a+3)
a+3
(a-2)
a+2(a+2)(a-2)
+3
+2a+2
a+2
6-2=4时,
原式=4+2
11.先化简,再求值:2
+1),其中x
x-1>1
为整数且满足不等式组
2x≥2.
1+x-1
解:原式
(x+1)(x-1)
x-1
x+1)(x-1)
x+1
x-1>1,
22x≥2
x是整数,∴x=3
∴原式
3+14
考点4分式方程的解法及应用
12.方程
的解为
2. x
B.x=0
13.已知关于x的分式方程
x71的解是负
数,则m的取值范围是
B.m≤3且m≠2
D.m<3且m≠2
72
2mn+2
14.若关于x的方程
x-1x-2(x-1)(x-2)
无解,求m的值.
解:方程两边都乘(x-1)(x-2),得x-2+
m(x-1)=2m+2,化简得(m+1)x=3m+4
原分式方程无解,
当m+1=0且3m+4≠0时,m=-1
当x=1时,m+1=3m+4,解得m
当x=2时,2m+2=3m+4,解得m2=-2
宗上,m的值为-1或一。或
标题截图放置居中位置
考点1分式的相关概念及性质
1.若分式
有意义,则x的取值范围是(D)
A
D.x≠-2
2.若分式
的值为零,则x的值是(A
D.10
3.下列运算中,正确的是
A
n212+m
2ab
ab
b-b
b
b
b
4.分式
c m
ya2-b,x+中,最简分式有
A.1个B.2个C.3个D.4个
考点2负整数指数幂与科学记数法
5.(硚口区)下列等式正确的是
A.(-3)
B.4
4
0.0000618=6.18×10
D.20-1=1
6.新型冠状病毒的直径是100nm(1nm
10m),则新型冠状病毒的直径用科学记数
法表示是
A.10-8m
B.10-2nm
C.10
D.10
计算:(2m2n-3)=2·(
解:原式=2-2m4n
36
2n2
4+3-(-6)6+6-2
2214
2510
2n2
考点3分式的运算及化简求值
8.下列各式计算错误的是
Bab lo.r
4r
21b
14x
xy. 3xy 4y
y
3.3
b
ab)
C
b
4a+4
9.当a=2020时,计算
4
的结果是
(B)
A.2019
B.2020
D.2021
2020
10.(朝阳)先化简,再求值:
2-4
2a+6
Q,其中
212
2
+3
2(a-2)2
解:原式
a+2(a+2)(a-2)2(a+3)
a+3
(a-2)
a+2(a+2)(a-2)
+3
+2a+2
a+2
6-2=4时,
原式=4+2
11.先化简,再求值:2
+1),其中x
x-1>1
为整数且满足不等式组
2x≥2.
1+x-1
解:原式
(x+1)(x-1)
x-1
x+1)(x-1)
x+1
x-1>1,
2
x是整数,∴x=3
∴原式
3+14
考点4分式方程的解法及应用
12.方程
的解为
2. x
B.x=0
13.已知关于x的分式方程
x71的解是负
数,则m的取值范围是
B.m≤3且m≠2
D.m<3且m≠2
72
2mn+2
14.若关于x的方程
x-1x-2(x-1)(x-2)
无解,求m的值.
解:方程两边都乘(x-1)(x-2),得x-2+
m(x-1)=2m+2,化简得(m+1)x=3m+4
原分式方程无解,
当m+1=0且3m+4≠0时,m=-1
当x=1时,m+1=3m+4,解得m
当x=2时,2m+2=3m+4,解得m2=-2
宗上,m的值为-1或一。或
