11.2.1第2课时直角三角形的两个锐角互余 习题课件
文档属性
| 名称 | 11.2.1第2课时直角三角形的两个锐角互余 习题课件 |

|
|
| 格式 | pptx | ||
| 文件大小 | 2.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2021-12-07 09:17:17 | ||
图片预览





文档简介
(共14张PPT)
知识要点全练
夯奥基础
知识点1直角三角形的两个锐角互余
在一个直角三角形中,若一个锐角等于60°,则
另一个锐角的度数是
(D)
A.120°B.90
C.60
D.30°
2.如图,BC⊥AE于点C,CD∥AB,∠B=55°,
则∠1等于
A.55°
B.45°
C.35
D.25°
E
(第2题图)
(第3题图)
ED
E
A
B
B
(第2题图)
(第3题图)
3.如图,在△ABC中,CE,BF是两条高.若∠A
70°,∠BCE=30°,则∠EBF
20
∠FBC=40°
知识点2有两个角互余的三角形是直角三角形
4.若四个三角形分别满足以下条件:①∠A
∠B=∠C;②∠A-∠B=∠C;③∠A=∠B
2∠C;④∠A:∠B:∠C=1:2:3,则其中直角
角形的个数是
(B)
A.1
B.2
D.4
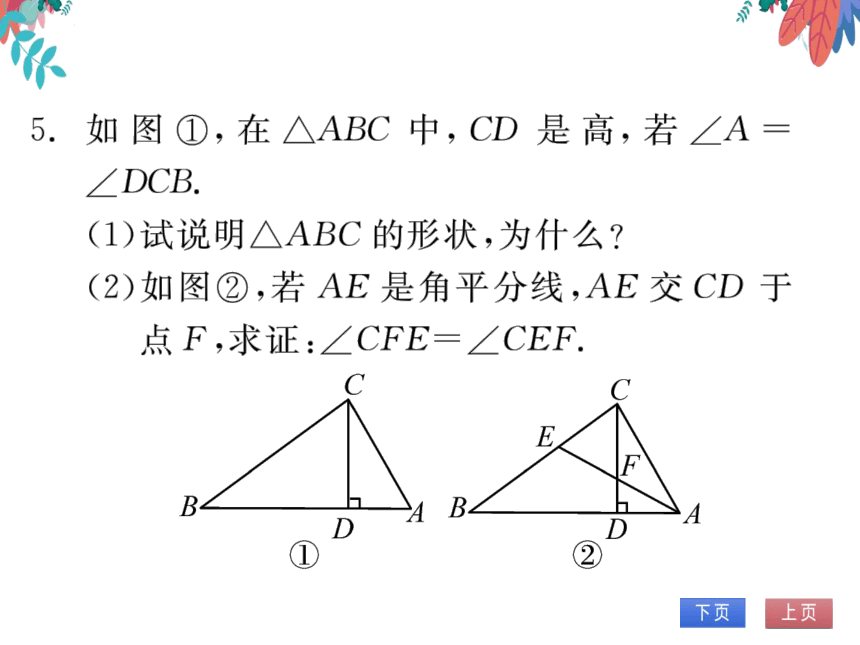
5.如图①,在△ABC中,CD是高,若∠A
∠DCB
(1)试说明△ABC的形状,为什么
(2)如图②,若AE是角平分线,AE交CD于
点F,求证:∠CFE=∠CEF
1)解:△ABC为直角三角形,理由如下:
∴CD是高,∠CDB=90°
∠B+∠BCD=90°
A=∠DCB,∴∠A+∠B=90
△ABC是直角三角形
(2)证明:∵AE是角平分线,∠CAE=∠EAB
由(1)知:∠ACB=90°,∴∠CEF+∠CAE=90
∠EAB+∠AFD=90°,∴∠CEF=∠AFD.
又∵∠AFD=∠CFE,∠CFE=∠CEF.
篇舰律方法全练多
提升能力
6.(抚顺)一副直角三角尺如4
图摆放,点D在BC的延长
线上,EF∥BC,∠B
F
∠EDF=90°,∠A=30°,
F=45°,则∠CED的度数
疋
A.15°
B.25°
C.45°
D.60
(教材P17习题T10变式)如图,AB∥CD,直
线EF分别交AB,CD于点E,F,∠BEF的平
分线与∠DFE的平分线相交于点P,试说明
△EPF为直角三角形
解:∵AB∥CD,
∠BEF+∠DFE=180
∴EP为∠BEF的平分线,
FP为∠EFD的平分线,
∠PEF=∠BEF,∠PFE
1/DFE
∠PEF+∠PFE=1
∠BEF+∠DFE)
90.∴△EPF为直角三角形
各探究创新全练
挑战自我
8.如图①,在△ABC中,AD⊥BC于点D,CE
AB于点E
(1)猜测∠1与∠2的关系,并说明理由;
(2)如果∠ABC是钝角,如图②,(1)中的结论
是否还成立 请说明理由
知识要点全练
夯奥基础
知识点1直角三角形的两个锐角互余
在一个直角三角形中,若一个锐角等于60°,则
另一个锐角的度数是
(D)
A.120°B.90
C.60
D.30°
2.如图,BC⊥AE于点C,CD∥AB,∠B=55°,
则∠1等于
A.55°
B.45°
C.35
D.25°
E
(第2题图)
(第3题图)
ED
E
A
B
B
(第2题图)
(第3题图)
3.如图,在△ABC中,CE,BF是两条高.若∠A
70°,∠BCE=30°,则∠EBF
20
∠FBC=40°
知识点2有两个角互余的三角形是直角三角形
4.若四个三角形分别满足以下条件:①∠A
∠B=∠C;②∠A-∠B=∠C;③∠A=∠B
2∠C;④∠A:∠B:∠C=1:2:3,则其中直角
角形的个数是
(B)
A.1
B.2
D.4
5.如图①,在△ABC中,CD是高,若∠A
∠DCB
(1)试说明△ABC的形状,为什么
(2)如图②,若AE是角平分线,AE交CD于
点F,求证:∠CFE=∠CEF
1)解:△ABC为直角三角形,理由如下:
∴CD是高,∠CDB=90°
∠B+∠BCD=90°
A=∠DCB,∴∠A+∠B=90
△ABC是直角三角形
(2)证明:∵AE是角平分线,∠CAE=∠EAB
由(1)知:∠ACB=90°,∴∠CEF+∠CAE=90
∠EAB+∠AFD=90°,∴∠CEF=∠AFD.
又∵∠AFD=∠CFE,∠CFE=∠CEF.
篇舰律方法全练多
提升能力
6.(抚顺)一副直角三角尺如4
图摆放,点D在BC的延长
线上,EF∥BC,∠B
F
∠EDF=90°,∠A=30°,
F=45°,则∠CED的度数
疋
A.15°
B.25°
C.45°
D.60
(教材P17习题T10变式)如图,AB∥CD,直
线EF分别交AB,CD于点E,F,∠BEF的平
分线与∠DFE的平分线相交于点P,试说明
△EPF为直角三角形
解:∵AB∥CD,
∠BEF+∠DFE=180
∴EP为∠BEF的平分线,
FP为∠EFD的平分线,
∠PEF=∠BEF,∠PFE
1/DFE
∠PEF+∠PFE=1
∠BEF+∠DFE)
90.∴△EPF为直角三角形
各探究创新全练
挑战自我
8.如图①,在△ABC中,AD⊥BC于点D,CE
AB于点E
(1)猜测∠1与∠2的关系,并说明理由;
(2)如果∠ABC是钝角,如图②,(1)中的结论
是否还成立 请说明理由
